
кадр из х/ф Феномен
Но вот недавно сын подошел после олимпиады по «Финансовой грамотности» на ресурсе «ЯКласс», где после окончания выложили результаты и решения, с вопросом почему его решение неправильное. Рассмотрев решение от авторов и решение сына, погрузился в решения и уточнения, получив неоднозначные результаты. Эта ситуация напомнила мне мою молодость и не согласие со многими классическими задачами и их решениями. Далее под катом эта и другие задачи, в которых включается режим зануды.
Вот текст задачи
За какое время окупятся куры? (задача из «Арифметики» Леонтия Магницкого)
Один человек купил трёх кур и заплатил за них 45 копеек. Первая курица несла по 2 яйца за 4 дня, вторая — по 2 яйца за 3 дня, а третья — по 1 яйцу за 2 дня. Продавал он яйца по 5 штук за полкопейки. За какое время окупятся куры? Запиши ответ числом без точки.
Даже если вы ещё не посмотрели решение, думаю для вас очевидна логика решения данной задачи с точки зрения математики, большинство из вас решат её даже в голове. Но олимпиада проводиться по Финансовой грамотности, и прочитав условия внимательно ещё раз начинают закрадываться смутные сомнения.
И действительно, вот купили мы три курицы каждая несется раз в сколько то дней, но в каком состоянии она сейчас, например первая, самая так сказать сложная в прогнозе. Может сегодня два яйца снесёт, может завтра, может вообще через три дня.
Вывод номер 1: С учётом условий задачи, каждая из трех куриц может находиться на момент в произвольном состоянии (1-я в одном из 4-х, 2-я в одном из 3-х, третья в одном из 2-х).
Вывод номер 2: Состояние куриц друг относительно друга тоже может быть разным.
Соответственно всего три курицы могут быть в одном из 24-х сочетаний состояний.
Но и это ещё не всё находясь в различных состояниях друг относительно друга, они несутся с разной периодичностью, следовательно в каждом сочетании есть цикличность, и этот цикл 12 дней. Курицы могут быть куплены нами в любой из дней 12-ти дневного цикла.
Итог у нас может быть 288 различных сочетаний, несомненно многие из них повторяются, это теоретический предел.
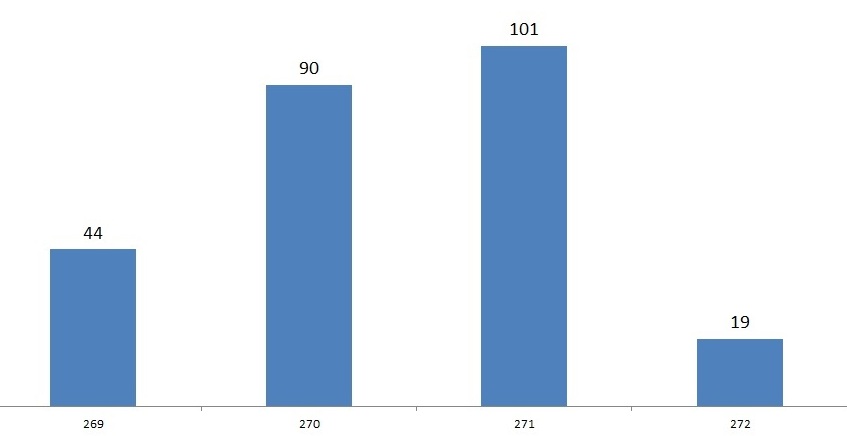
Имея все эти данные, достаточно просто составить таблицы того как несутся куры во всех вариантах, в результате чего мы узнаем что на самом деле срок окупаемости варьируется от 269 дней до 272 дней. Проанализировав все варианты получаем следующую гистограмму распределения по дням окупаемости:
В итоге верный ответ на данную задачу по финансовой грамотности (с моей точки зрения) должен звучать так:
В 17,3 % случаев срок окупаемости будет 269 дней;
В 35,4 % случаев срок окупаемости будет 270 дней;
В 39,8 % случаев срок окупаемости будет 271 день;
В 7,5 % случаев срок окупаемости будет 272 дня.
На картинке в начале запечатлен кадр из фильма «Феномен» (1996 – Phenomenon), и этот эпизод как раз про похожую ситуацию, когда вроде бы оригинальные вопросы, на определенном уровне восприятия показывают ограниченность их предыдущего рассмотрения.
Никакого ответа от службы поддержки «ЯКласс», получено не было, хотя ситуацию описал подробно с приложением расчётов в excel, что конечно огорчило формализмом в таком важном деле как развитие детей.
Такая задача не исключение, мне в школе всегда не нравилась другая задача: «Имеется три слова: Кошка, Солнце, Близко. Какое слово лишнее?». После прохождения тестирования, узнал, что лишнее слово Близко, потому что прилагательное. Я же руководствовался логикой количества букв и лишним посчитал слово КОШКА. Если посидеть и подумать можно придумать ещё несколько логических исключений любого слова в представленном примере (мы с сыном придумали пять вариантов). И вот у ребенка возникает вопрос, чем мои логические измышления хуже чем у автора теста.
Очень много дискуссий вызывает задача: На стене висят часы, у которых минутная и часовая стрелка совпадают каждые 65 минут, в точности. Они спешат, отстают или идут правильно?
Должны ли мы приводить мышление детей к общим стандартам, чтобы он вписался в социум, или надо поддерживать креативность и широту мысли. Как всегда истина где-то по середине, но думаю без нестандартной логики, что то выдающееся в этом мире не сделать.


janvarev
Да, и вы тоже пострадали от формального подхода к олимпиадным задачам.
У меня была совершенно феерическая история. На олимпиаде по программированию надо было запрограммировать ход пешки на шахматной доске. Пара человек, и я в том числе, добавили очевидную для шахматиста проверку «нельзя бить короля».
На тестах оказалось, что мы прошли только 1 или 2 начальных. Почему? Потому что все следующие начинались с хода пешки, которая затем била именно короля! На вопрос: «А почему так?» был получен феерический ответ, что «В условии задачи не было, что короля бить нельзя.»
Почему в таком случае нельзя было составить тесты вообще без этой фигуры (если потенциально здесь могла быть неоднозначность), осталось непонятным.
— Другая задача, по физике, условно начиналась со слов «Бесконечно длинная цепь бесконечно падает...». Её не решил никто.
Fedorkov
Тест с королём под боем некорректен, но всё же в шахматах нет правила «нельзя бить короля».
Ещё в условии должен быть пункт «нельзя брать на проходе», иначе некоторые тесты не будут иметь однозначного решения.
janvarev
Ну, в шахматах по правилам нет ситуаций, где можно бить короля.
Просили запрограммировать ход + возможность взятия фигуры, и была добавлена логичная проверка на то, что фигура — не король, и такой ход невозможен.
Tsimur_S
Все правильно, в самих шахматах такой ситуации не может быть но и запрета в правилах на то кого можно бить а кого нельзя нет. Тут нету никакого противоречия. Это как в задаче про ферзей, их же не может быть в шахматах больше чем 18(по 8пешек+ферзь с каждой стороны)? Следует ли из этого что ответ задачи про максимальное число ферзей не находящихся под боем на шахматной доске ограниченна сверху 18?