В этой статье я расскажу как написать свою реализацию известной игрушки Сокобан, а также алгоритм для её решения с нуля. Заодно применю на практике некоторые шаблоны проектирования и принципы SOLID.

Весь код расположен по адресу

Предыстория

Я пользуюсь кнопочным телефоном. Из развлечений на нём только радио и единственная игра Сокобан из 15 уровней. Из них я решил только 10 и застрял на одиннадцатом. Как-то раз я целый день ехал в поезде и решал этот злосчастный 11 уровень, но не преуспел. Тогда я решил прибегнуть к помощи компьютера, благо опыт программирования имею достаточный для такой задачи. Поставил цель: самостоятельно написать реализацию с решением этой игрушки. По результатам появилась эта статья.

Тот самый 11 уровень (решение в конце статьи):

Сама игрушка представляет собой прямоугольное 2D-поле, на котором раскиданы ящики, стены и метки. Ящики можно толкать, но не тянуть, в этом вся сложность. Ваша цель: переместить все ящики на клетки с метками. Пример игры:

Пишем реализацию

Давайте не будем усложнять себе задачу и создавать отдельный GUI со спрайтами и редактором уровней. Вместо этого остановимся на консольном варианте а-ля Rogue-like, где уровни будут отрисовываться построчно и загружаться из текстового файла. Сначала нужно придумать какие символы будут обозначать элементы на уровне. Я сделал такой выбор:

• Решётка # это стена, через неё нельзя пройти и продвинуть ящик.
• Буква O это ящик.
• Буква X это метка, куда нужно переместить ящик.
• Собака @ означает игрока.
• Точка . означает пустое место.
• Буква G это ящик на метке.

Теперь самый ответственный момент — выбор архитектуры приложения. Если ошибиться, то можно сильно повредить всей дальнейшей разработке. В нашем случае идеально подходит шаблон MVC — Модель, Представление, Контроллер. Модель хранит внутреннее игровое состояние и поле, даёт доступ к данным, не знает ничего о контроллере и представлении. Представление только печатает состояние модели в консоль. Контроллер считывает символы с клавиатуры и изменяет модель. Типичная ошибка новичков — добавлять бизнес-логику в контроллер вместо модели. В результате получаются переполненные чужим кодом контроллеры, нарушающие первую букву SOLID. Согласно ей, каждый класс должен брать на себя только одну ответственность. Представление — печатать уровни в консоль, модель — хранить состояние игрушки и логику работы с ним, контроллер — обрабатывать действия пользователя. То есть контроллер не должен знать как именно двигать ящики и игрока по полю, это ответственность модели. Контроллеру всего лишь нужно вызвать соответствующий метод. Ещё хорошо бы скрыть реализации всех трёх сущностей за интерфейсами. Это даёт следующее:

• Можно спокойно менять реализации, например, написать GUI-представление. На остальной код это никак не повлияет.
• В совокупности с инъекцией зависимостей значительно упрощается модульное тестирование.

Вторая частая ошибка новичков в ООП — компоненты сами управляют своими зависимостями, например создают экземпляры конкретных реализаций интерфейсов в конструкторах:

public class ConsoleController implements Controller
{
    private final Model model;
    private final View view;

    public ConsoleController(final Model model)
    {
        this.model = model;
        this.view = new ConsoleView(model);
    }
    // methods
}

Здесь первая зависимость model была установлена как надо, через ссылку в параметре конструктора, а вторая view создана напрямую. Это плохо хотя бы потому, что теперь ConsoleController должен знать не только о View, но и ConsoleView, что повышает зацепление. Изменения ConsoleView могут повлечь за собой изменения в ConsoleController, чего можно избежать, написав вот так:

public class ConsoleController implements Controller
{
    private final Model model;
    private final View view;

    public ConsoleController(final Model model, final View view)
    {
        this.model = model;
        this.view = view;
    }
    // methods
}

Теперь класс ConsoleController стало проще тестировать. Суть буквы D в SOLID в том, что класс не должен контролировать как именно удовлетворяются его зависимости. Эта ответственность теперь ложится на клиентов класса. Есть множество механизмов разрешения зависимостей, самый популярный из которых — контейнер зависимостей. Это отдельный модуль, обычно реализованный каким-нибудь фреймворком типа Spring или библиотекой, который сам может прокинуть все необходимые экземпляры в конструкторы или сеттеры. От вас нужно только их объявить.

Нужно придумать что из себя вообще представляет модель игрушки. Посмотрим ещё раз на скриншот, что мы видим?

• Квадратное поле из различных плиток
• Набор ящиков и меток
• Игрока
  Каждую клетку на поле можно моделировать двумерным вектором (row, col), где row это номер строки, а col столбца клетки, начиная с нуля. Каждой клетке будет соответствовать плитка — пустое место, куда можно сходить или стена. Ящики не пронумерованы, любой ящик можно поставить на любую метку, поэтому можно смоделировать их как множества клеток, на которых расположены ящики и метки. Позиция игрока также моделируется клеткой.

Было бы логично научить модель саму себя решать, то есть поместить алгоритм поиска решения внутри модели. Однако, если мы захотим иметь несколько таких алгоритмов и сравнивать их между собой, то будет лучше вынести их в отдельный модуль, скрытый за интерфейсом. В этом суть шаблона "Стратегия" — выносить несколько реализаций одной функции в отдельные классы и прятать их под общим интерфейсом, потому что клиенту в большинстве случаев всё равно как именно вычисляется ваша функция, он хочет просто получить результат. У меня получилось вот такая архитектура:

Заметьте, здесь модель представлена не одним классом, а целым пакетом Model. Главный класс Sokoban не скрыт за интерфейсом, потому что представляет единственную реализацию модели игрушки. Метод move() двигает игрока в одну из четырёх сторон. Сам Sokoban можно изменить только вызвав этот метод. Методы getCrates() и getMarks() возвращают неизменяемое представление множеств. Забегая вперёд, скажу что я сразу заложил два алгоритма решения Сокобана: обход графа конфигураций в ширину и поиск оптимального пути от начальной конфигурации до выигрышной с помощью A* (A star algorithm).

Метод run() запускает цикл "отрисовка уровня -> считывание движения -> обновление модели -> снова отрисовка"

Уровни будут загружаться из текстового файла со строками символов клеток, например:

###########
#.@..O..X.#
###########

Чтение и парсинг файла лучше тоже вынести в отдельный класс-создатель модели. Здесь идеально подходит шаблон "Абстрактная фабрика". Вкратце: внутри класса CharSokobanFactory пишем код чтения и парсинга файла, создаём игрока, поле, множество меток и ящиков. Важно, чтобы конструктор класса Sokoban оставался чистым, то есть содержал только присвоения зависимостей, это упрощает тестирование:

    public Sokoban(final Field field, final Set<Point> crates, final Set<Point> marks, final Point player)
    {
        this.field = field;
        this.crates = crates;
        this.marks = marks;
        this.player = player;
    }

Созданием этих зависимостей как раз и займётся CharSokobanFactory. Фабрику нужно скрыть за интерфейсом, чтобы не привязываться к созданию модели через символьные строки. В будущем можно использовать другой формат хранения уровней.

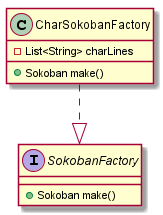
Вместо стрелок я решил выбрать vi-like раскладку:

• Буква j — шаг вниз
• Буква k — вверх
• Буква h — влево
• Буква l — вправо

Игра считается завершённой, если множества ящиков и меток равны:

class Sokoban {
    // some stuff
    public boolean solved()
    {
        return marks.equals(crates);
    }
    // other stuff
}

Чтобы не городить кучу свичей и if-ов в контроллере, я создал перечисление Direction, где выписал какой символ отвечает за какое направление. Затем создал класс Move, который инкапсулирует Direction и вызывает метод move(direction) у модели. Также у него есть статичный метод Move.resolve, который создаёт экземпляр по клавише пользователя.
Это хороший пример шаблона "Фабричный Метод". Плюс такого подхода: если я захочу чтобы игрок мог ходить по диагонали, то мне нужно будет добавить только 4 строчки в перечисление.
Таким образом соблюдается буква O в SOLID, Open-Closed Principle: классы должны быть открыты для расширений и закрыты для изменений. То есть, мы должны иметь возможность добавлять новый функционал без изменения старого. Очень часто происходит так, что новые фичи ломают старые, а исправления ошибок только вводят новые. Это как раз из-за того, что программисты не знают как правильно изолировать различные аспекты задачи по классам так, чтобы изменения одних не затрагивали другие.

Получается такая схема:

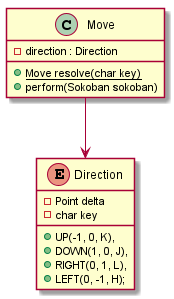
С такой архитектурой код контроллера становится очень простым:

class ConsoleController {
//
    @Override
    public void run()
    {
        view.say("Sokoban Starts");
        char symbol = '0';
        view.render();
        final List<Move> history = new LinkedList<>();
        while (symbol != 'q')
        {
            final Move move = Move.resolve(symbol);
            if (move != null)
            {
                history.add(move);
                move.perform(sokoban);
                view.render();
                if (sokoban.solved())
                {
                    view.say("YOU WIN!");
                    break;
                }
            }
            try
            {
                symbol = (char) System.in.read();
            }
            catch (IOException io)
            {
                view.say("Не получилось считать команду:");
                throw new IllegalStateException(io);
            }
        }
        view.say("Your moves: " +  Move.compress(history));
    }
//
}

Красота, как обычно, в мелочах. Как я уже говорил в начале статьи, контроллер не должен содержать никакой бизнес-логики, только читать команды от пользователя, перенаправлять их модели и отрисовывать представление. Такая реализация как раз не содержит ничего лишнего.

Реализация представления тоже проста до невозможности:

class ConsoleView {
//
    @Override
    public void render()
    {
        clearConsole();
        for (int i = 0; i < sokoban.numberOfFieldRows(); i++)
        {
            for (int j = 0; j < sokoban.numberOfFieldCols(); j++)
            {
                final Point at = new Point(i, j);
                final Tile tileAt = sokoban.tile(at);
                if (tileAt == null)
                    break;
                final char symbolToPrint = tileAt == Tile.CRATE && sokoban.isMarkAt(at) ? Tile.CRATE_ON_MARK.symbol() : tileAt.symbol();
                System.out.print(symbolToPrint);
            }
            System.out.println();
        }
    }
//
}

Строка 15 обрабатывает клетку с ящиком на метке. Буква G (Good) специально предназначена, чтобы обозначать ящик, задвинутый на метку. Однако такая клетка никак не моделируется, поэтому существует только в представлении.

Остаётся только научить модель передвигать игрока. Нужно учесть следующие моменты:

• Нельзя ходить в стену и в неподвижный ящик
• Ящик двигается в ту же сторону, что и игрок. Поэтому если перед ящиком стена или другой ящик, то двигать его нельзя.

Проверить эти условия несложно, в этом поможет флаг "walkable" в перечислении Tile:

public enum Tile {
    WALL('#', false),
    GRASS('.', true),
    CRATE('O', false),
    MARK('X', true),
    CRATE_ON_MARK('G', false),
    PLAYER('@', true);

    private final char symbol;
    private final boolean walkable;

    Tile(final char symbol, final boolean walkable) {
        this.symbol = symbol;
        this.walkable = walkable;
    }

    public boolean isWalkable() {
        return walkable;
    }
}

Тогда проверка на то, можно ли сходить на данную ячейку сократится до нескольких строк:

public Sokoban {
// класс Sokoban
    public Tile tile(final Point at) {
        if (player.equals(at))
            return Tile.PLAYER;
        //
        if (crates.contains(at))
            return Tile.CRATE;
        //
        return field.tileAt(at);
    }
    public boolean isWalkableTileAt(final Point at) {
        return tile(at).isWalkable();
    }
// класс Sokoban
}

Итак, модель умеет передвигать игрока, контроллер обрабатывать команды пользователя, а представление рисовать уровни в консоль. Самое время собрать всех вместе и запустить:

public class Main {
    public static void main(String[] args) {
        final Sokoban sokoban = CharSokobanFactory.fromFile(args[0]).make();
        final View view = new ConsoleView(sokoban);
        final Controller game = new ConsoleController(sokoban, view);
        // запуск
        game.run();
    }
}

Для теста возьмём вот этот уровень:

############
#.XO.......#
#.XO......@#
#.XO.......#
############

В результате получаем именно то, что хотим:

Как и ожидалось, в стены ходить нельзя, ящики передвигаются как надо, игра заканчивается как только третий ящик оказывается на метке. Вот так просто можно написать простую игрушку Сокобан. Однако, самое сложное ещё впереди — нужно научить компьютер её решать.

Пишем свой искусственный интеллект

Что мы делаем когда передвигаем ящики в Сокобане? Мы меняем конфигурацию уровня. Конфигурация здесь это расположение игрока и ящиков на уровне. У каждой конфигурации есть несколько дочерних, в которые можно перейти, передвинув ящик на соседнюю клетку:

Понятно, что когда игрок просто двигается по уровню не трогая ящики, то конфигурация не изменится. Мы не перейдём в другую вершину графа. Можно было бы предположить, что позиция игрока вообще не имеет значения, и в конфигурацию входит только множество точек ящиков, но это не так. Позиция игрока не важна только пока он передвигается по одной компоненте связности внутри уровня. Кроме графа конфигураций, есть ещё граф инцидентных
клеток для конкретной конфигурации, например:

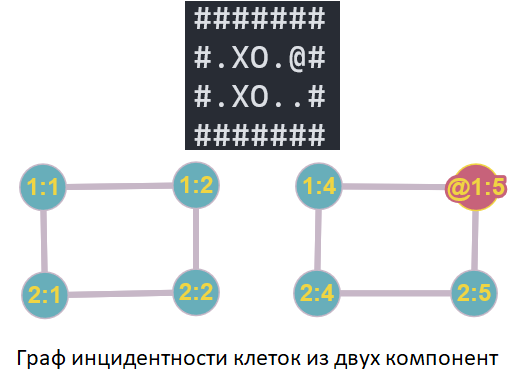
Игрок может перемещаться только по правой компоненте не трогая ящики, конфигурация от этого не изменится. Однако, если поместить игрока на клетку (1:1), он попадёт в левую и решить такой уровень будет невозможно.

Игра в Сокобан представляет собой прогулку по графу конфигураций в поиске выигрышной вершины. Решение — это путь в таком графе от начальной конфигурации до выигрышной.
Рёбра в графе помечены шагами игрока от его исходной позиции до передвижения ящика. Вес ребра это количество таких шагов. Нам интересно не просто определить имеет ли решение конкретный уровень, но ещё и найти это самое решение. В зависимости от уровня такой граф может иметь любую структуру, поэтому нам нужен алгоритм поиска пути, работающий для любых графов. Если забыть что рёбра взвешенные, то отлично подойдёт алгоритм поиска в ширину — Breadth-First Search (BFS).

Поиск решения с помощью BFS

В отличие от своего "кузена" — поиска в глубину (Depth-First Search) — в невзвешанном графе BFS строит кратчайшие пути от исходной вершины до всех достижимых, постепенно выращивая дерево родителей. Кстати, эти два алгоритма отличаются только порядком извлечения вершин из списка. BFS извлекает вершины в порядке очереди (FIFO), а DFS в порядке стека (LIFO), то есть это по сути один и тот же алгоритм. Псевдокод BFS:

BFS(G, s)
1. Инициализировать граф, поставить у каждой вершины:
    * v.p = null // преды
    * v.marked = false // посещали ли уже эту вершину
2. Создать очередь Q
3. Q.enqueue(s)
4. Пока Q не пуста:
    4.1 v = q.poll()
    4.2 v.marked = true
    4.3 Если v это искомая вершина, то прекратить выполнение
    4.4 Цикл по всем инцидентным v вершинам, child:
        4.4.1 Если не child.marked, то:
            4.4.1.2 child.p = v
            4.4.1.3. q.enqueue(child)

Здесь параметр v.p указывает на предшествующую ей вершину на пути от начальной до v. Поднятый флаг v.marked показывает, что v уже посещали. Чтобы воссоздать кратчайший путь до v надо "промотать" список v -> v.p -> v.p.p -> ... -> s до начальной задом-наперёд. Под искомой здесь понимается вершина с решённой конфигурацией.

Нам нужно уметь порождать все соседние конфигурации из данной. Каждая соседняя конфигурация порождается движением ящика в одну из четырёх сторон. Причём по бокам
клетки должны быть пустыми. Например, если двигать ящик вправо, то надо чтобы игрок мог добраться до клетки слева от ящика и чтобы справа была свободная клетка. Аналогично с вертикальным движением. Также при проверке можно отсекать заведомо проигрышные конфигурации, когда ящик прислоняется к стене без дальнейшей возможности движения:

Комбинируя все замечания, получаем вот такой код:

public class BFSSolver {
//
    protected List<Pair<Sokoban, List<Direction>>> deriveChildren(final Sokoban parent) {
        final Map<Point, Point> walkablePoints = shortestPathsFromPlayer(parent);
        final List<Pair<Sokoban, List<Direction>>> result = new LinkedList<>();
        for (final Point crate : parent.getCrates()) {
            final Point[][] pairs = new Point[][]{{crate.left(), crate.right()}, {crate.right(), crate.left()},
                    {crate.up(), crate.down()}, {crate.down(), crate.up()}};
            for (Point[] pair : pairs) {
                final Point playerWillStand = pair[0];
                final Point crateWillGo = pair[1];
                if (canMoveCrate(parent, playerWillStand, crateWillGo, walkablePoints) && !isDeadPosition(parent, crateWillGo)) {
                    final LinkedList<Direction> pathToChild = unwindWalk(walkablePoints, playerWillStand);
                    pathToChild.add(crate.derive(crateWillGo));
                    final Sokoban child = parent.derive(crate, crateWillGo);
                    result.add(Pair.pair(child, pathToChild));
                }
            }
        }
        return result;
    }
//
}

На первой строчке метод shortestPathsFromPlayer создаёт дерево предшественников в кратчайших путях от parent до всех достижимых вершин. Словарь walkablePoints отображает клетки v на v.p. Метод isDeadPosition как раз проверяет чтобы конфигурация не была заведомо проигрышной. Метод derive из класса Sokoban создаёт "копию" конфигурации со сдвинутым ящиком:

    public Sokoban derive(final Point crateToRemove, final Point crateToInsert)
    {
        final Set<Point> childConfiguration = new HashSet<>(crates);
        childConfiguration.remove(crateToRemove);
        childConfiguration.add(crateToInsert);
        return new Sokoban(this.field, childConfiguration, Collections.unmodifiableSet(this.marks), crateToRemove);
    }

Обратите внимание, что "порождённая" таким методом копия не меняет множество меток. Кстати, класс Point я специально сделал неизменяемым (immutable). Нет смысла создавать отдельную структуру данных "Граф", заполнять его вершинами и рёбрами, а потом уже запускать BFS, это только пустая трата циклов процессора. Свойства v.p и v.marked можно симулировать ассоциативным словарём и множеством.

Теперь у нас в арсенале есть всё необходимое для реализации самого алгоритма:

public class BFSSolver {
//
    public List<Move> solve(final Sokoban start) {
        final Map<Sokoban, Pair<Sokoban, List<Direction>>> childToParentAndDirection = new HashMap<>();
        final Set<Sokoban> visited = new HashSet<>();
        final Queue<Sokoban> toVisit = new LinkedList<>();
        toVisit.add(start);
        boolean found = false;
        Sokoban parent = null;
        while (!toVisit.isEmpty()) {
            parent = toVisit.remove();
            if (parent.solved()) {
                found = true;
                break;
            }
            visited.add(parent);
            for (final Pair<Sokoban, List<Direction>> pair : deriveChildren(parent)) {
                final Sokoban child = pair.first;
                final List<Direction> walkFromParentToChild = pair.second;
                if (!visited.contains(child)) {
                    childToParentAndDirection.put(child, Pair.pair(parent, walkFromParentToChild));
                    toVisit.add(child);
                }
            }
        }
        return found? unwind(parent, childToParentAndDirection) : new LinkedList<>();
    }
//
}

Такой алгоритм находит решение, но далеко не факт что оно будет оптимальным, потому что BFS не учитывает вес ребра, то есть рассматривает граф конфигураций как невзвешенный. Чтобы найти наименьший путь во взвешенном графе можно взять, например, алгоритм Дейкстры, однако тут есть одна загвоздка. Понятно, что даже у простого уровня граф конфигураций может быть гиганским, а оптимальный путь чуть ли не единственным. Алгоритм,
который будет рассматривать вообще "весь" граф, будет работать слишком долго. Причём в графе будет много тупиковых ветвей, куда заходить вообще не надо. Было бы здорово указать на это машине.

На помощь приходит алгоритм А* (A star), который по сути является Дейкстрой с одним отличием. А* вводит т.н. эвристическую функцию h оценки расстояния от текущей вершины до решения. Значение h складывается с текущей оценкой пути. Идея следующая — если алгоритм заходит на одну из таких тупиковых ветвей, то большое значение h превысит текущее оптимальное и алгоритм просто дальше не пойдёт. Нужно только придумать достаточно
"хорошую" эвристику. Я взял сумму расстояний ящиков до ближайших к ним меток. Класс AStarSolver реализует описанную логику. Код преводить не буду чтобы не загружать статью, всё есть по адресу.

Чтобы запустить новый алгоритм ИИ я написал новый контроллер AIController, который не читает команды из консоли, а решает уровень указанным алгоритмом и по таймеру проигрывает решение. нужно изменить всего одну строчку в main. Наши инвестиции в архитектуру окупились:

public class Main {
    public static void main(String[] args) {
        final Sokoban sokoban = CharSokobanFactory.fromFile(args[0]).make();
        final View view = new ConsoleView(sokoban);
        final Solver solver = new AStarSolver();
        final int sleepBetweenMovesMillis = 300;
        final Controller game = new AIController(sokoban, view, sleepBetweenMovesMillis, solver);
        // запуск
        game.run();
    }
}

Выводы

Мы создали свою реализацию игрушки Сокобан, применили на практике шаблоны проектирования "Абстрактная Фабрика", "Фабричный Метод", "Стратегия", рассмотрели принципы S, O и D из SOLID и реализовали алгоритмы BFS и A*.

Буду рад любым комментириям как по коду, так и по самой статье. Увидимся!

Я в телеграмме: @outofbound