Сегодня вместо обсуждения геологических моделей мы посмотрим пример их программирования в среде Jupyter Notebook на языке Python 3 и с библиотеками Pandas, NumPy, SciPy, XArray, Dask Distributed, Numba, VTK, PyVista, Matplotlib. Это довольно простой ноутбук с поддержкой многопоточной работы и возможностью запуска локально и в кластере для обработки больших данных, отложенными вычислениями (ленивыми) и наглядной трехмерной визуализацией результатов. В самом деле, я постарался собрать разом целый набор сложных технических концепций и сделать их простыми. Для создания кластера на Amazon AWS смотрите скрипт AWS Init script for Jupyter Python GIS processing, предназначенный для единовременного создания набора инстансов и запуска планировщика ресурсов на главном инстансе.

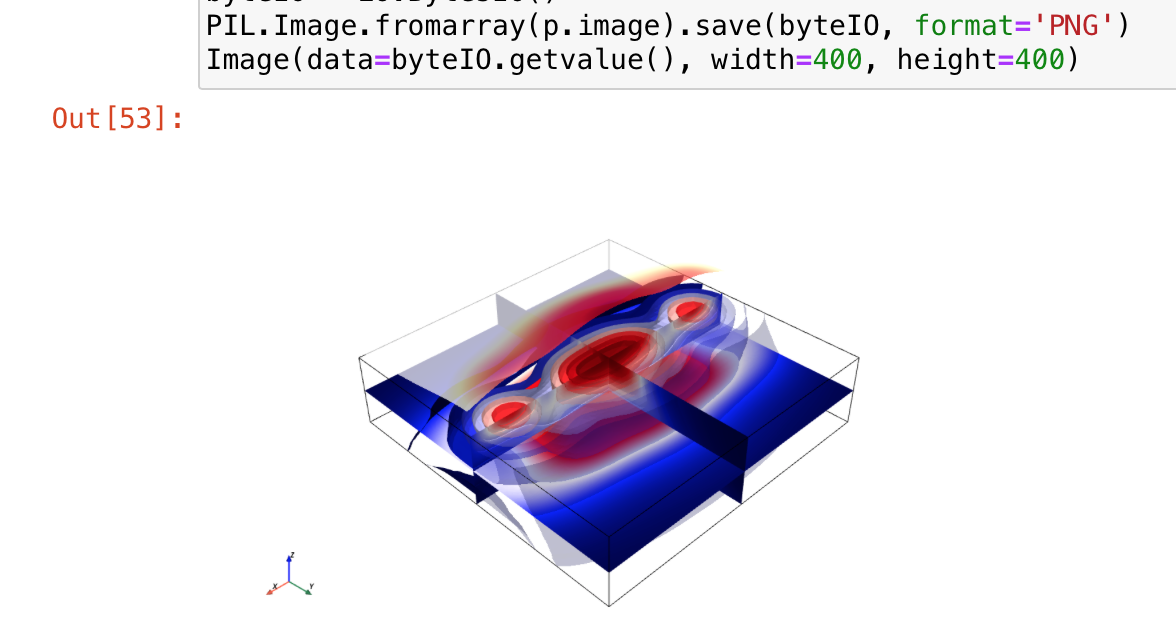
Визуализация с помощью Visualization Toolkit(VTK) и PyVista это уже далеко не Matplotlib

Идея сделать такой пример возникла у меня давно, поскольку я регулярно занимаюсь разнообразными вычислительными задачами, в том числе для различных университетов и для геологоразведочной индустрии, и знаком очень близко с проблемами переносимости и поддерживаемости программ, а также проблемами работы с так называемыми большими данными (сотни гигабайт и терабайты) и визуализацией результатов. Так что само собой появилось желание сделать ноутбук-пример, в котором коротко и просто показать и красивую визуализацию и распараллеливание и ускорение кода Python и чтобы этот ноутбук можно было без изменений запустить как локально, так и на кластере. Все использованные библиотеки доступны уже много лет, но мало известны, или, как говорится, они остаются широко известными в узких кругах. Оставалось лишь найти подходящую задачку, на которой все это можно показать и это было, пожалуй, самым сложным — ведь мне хотелось, чтобы пример получился достаточно осмысленным и полезным. И вот такая задача нашлась — рассмотреть моделирование гравитационного поля на поверхности для заданной (синтетической в данном случае) модели плотности недр и некоторые последующие преобразования с вычислением фрактального индекса по компонентам пространственного спектра и кольцевого преобразования Радона, как его называют математики, или Хафа, согласно компьютерным наукам. Замечательно то, что с популярными библиотеками Python эти преобразования делаются буквально в несколько строчек кода, что особенно ценно для примера. Поскольку моделирование поля в каждой точке поверхности требует вычисления для всего трехмерного объема, мы будем обрабатывать гигантский объем данных. Для визуализации используем человеколюбивую обертку PyVista для библиотеки VTK — Visualization Toolkit, потому что писать код для последней это путь истинных джедаев… кто хочет лично в том убедиться, смотрите мой модуль к ParaView N-Cube ParaView plugin for 3D/4D GIS Data Visualization, написанный как раз на Python + VTK.

Теперь предлагаю проследовать по ссылке на страницу GitHub репозитория или сразу открыть ноутбук basic.ipynb Надеюсь, код достаточно просто читается, остановлюсь лишь на нескольких особенностях. Запускаемый в ноутбуке локальный кластер dask предназначен для работы на многоядерных компьютерах, а вот для работы в кластере потребуется настроить подключение к его планировщику. В упомянутом выше скрипте AWS Init script for Jupyter Python GIS processing есть соответствующие комментарии и ссылки. В коде мы используем векторизацию NumPy, то есть передаем сразу массивы, а не скаляры, при этом пользуемся тем, что XArray объекты предоставляют доступ к внутренним NumPy объектам (object.values). Код NumPy ускорить непросто, но с помощью Numba и для такого кода можно получить некоторый выигрыш в скорости исполнения (возможно, даже около 15%):

from numba import jit
@jit(nopython=True, parallel=True)
def delta_grav_vertical(delta_mass, x, y, z):
    G=6.67408*1e-11
    return -np.sum((100.*1000)*G*delta_mass*z/np.power(x**2 + y**2 + z**2, 1.5))

Для перебора всех точек на поверхности куба и вычисления для каждой такой точки гравитационного воздействия от каждой точки куба (это, кстати, получается пятикратный интеграл) мы пишем:

def forward_gravity(da):
    (da_y, da_x, da_z) = xr.broadcast(da.y, da.x, da.z)
    deltagrav = lambda x0, y0: delta_grav_vertical(da.values.ravel(), (da_x.values.ravel()-x0), (da_y.values.ravel()-y0), (da_z.values.ravel()-0))
    gravity = xr.apply_ufunc(deltagrav, da_x.isel(z=0).chunk(50), da_y.isel(z=0).chunk(50), vectorize=True, dask='parallelized')
    ...

Здесь xarray.broadcast с линеаризацией массивов функцией ravel() позволяют из трех одномерных координат x, y, z получить триплеты координат для каждой точки куба. Выражения da_x.isel(z=0) и da_y.isel(z=0) извлекают x, y координаты верхней поверхности куба, на которой и вычисляется гравитационное поле (точнее, его вертикальную компоненту, т.к. именно она измеряется при практических исследованиях и такие данные доступны для анализа). Функция xarray.apply_ufunc() весьма универсальная и одновременно обеспечивает векторизацию и поддержку параллельных ленивых вычислений dask для указанной коллбэк функции deltagrav. Хитрость заключается в том, что для выполнения вычислений на кубе для каждой точки поверхности нужно координаты поверхности передать в виде XArray массивов, а для использования dask они также должны быть dask массивами, что мы и обеспечиваем конструкциями da_x.isel(z=0).chunk(50) и da_y.isel(z=0).chunk(50), где 50 это размер блока по координатам x, y (подбирается в зависимости от размера массивов и количества доступных вычислительных потоков). Да, такая вот магия — достаточно лишь использовать вызов chunk() для XArray массива, чтобы автоматически превратить его в dask массив.

Обратим внимание, что dask-вычисления по умолчанию являются ленивыми (отложенными), то есть вызов функции forward_gravity() завершается почти мгновенно, но возвращаемый результат является лишь оберткой, которая инициирует вычисления только при непосредственном обращении к данным или вызовом load(). При интерактивной работе это очень удобно, так как мы можем написать сложный пайплайн с большими наборами данных и для проверки и визуализации выбрать лишь маленький его кусочек, а при необходимости и запустить вычисления на полном наборе данных. К примеру, мне часто приходится работать с NetCDF датасетами глобального рельефа планеты и прочими в сотни гигабайт на своем ноутбуке — визуализируя малую часть данных, а потом запускать уже готовый ноутбук в облаке для обработки всех данных. Таким образом, код для локальной работы и его продакшен версия ничем не отличаются. Главное, правильно настроить размеры dask блоков, иначе вся магия "сломается".

Код кольцевого преобразования простой и полностью основан на стандартной двумерной свертке с кольцевой маской. Вот с вычислением фрактального индекса есть небольшой нюанс. А именно, здесь используется гауссова полосовая фильтрация исходного растра для выделения спектральных компонентов (диапазонов пространственных частот), мощность которых вычисляется как стандартное отклонение значений полученных матриц. Для нашей синтетической модели можно бы и попроще, а вот для реальных данных этот метод оказывается оптимальным в силу своей устойчивости к очень зашумленным данным и отсутствия проблем с границами. Далее стандартным способом вычисляется наклон кривой на двойном логарифмическом графике (логарифм длины волны и логарифм мощности компоненты).

В заключение, приглашаю всех посетить GitHub репозитории с множеством геологических моделей и их визуализацией в Blender и ParaView, а также примерами различного анализа. Также смотрите готовые визуализации на YouTube канале.