Добрый день. Сегодня хочется поговорить о том, как найти MEX (минимальное отсутствующие число во множестве).


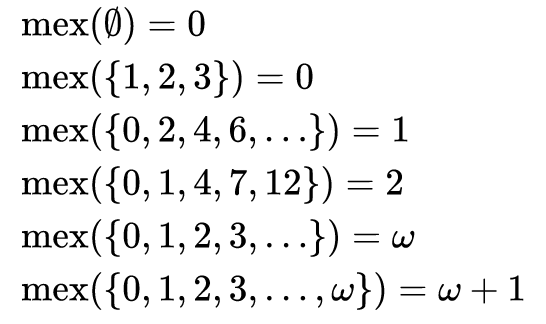
Мы разберем три алгоритма и посмотрим на их производительность.

Добро пожаловать под cut

Предисловие

Перед тем как начать, хотелось бы рассказать — почему я вообще за этот алгоритм взялся?
Всё началось с задачки на OZON.


Как видно из задачи, в математике результатом работы функции MEX на множестве чисел является наименьшим значением из всего набора, который не принадлежит этому множеству. То есть это минимальное значение набора дополнений. Название «MEX» является сокращением для «Minimum EXcluded» значение.


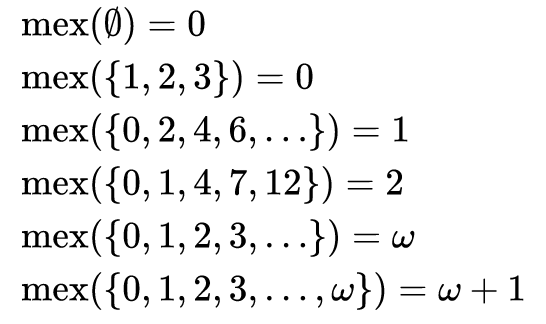
И покопавшись в сети, оказалось, что нет общепринятого алгоритма нахождения MEX…

Есть решения в лоб, есть варианты с дополнительными массивами, графами, но, как-то всё это раскидано по разным углам интернета и нет единой нормальной статьи по этому поводу. Вот и родилась идея — написать эту статью. В этой статье мы разберем три алгоритма нахождения MEX и посмотрим, что у нас получиться по скорости и по памяти.

Код будет на языке C#, но в целом там не будет специфичных конструкций.

Базовый код для проверок будет таким.

static void Main(string[] args)
        {
            //MEX = 2
            int[] values = new[] { 0, 12, 4, 7, 1 };
            
            //MEX = 5
            //int[] values = new[] { 0, 1, 2, 3, 4 };
            
            //MEX = 24
            //int[] values = new[] { 11, 10, 9, 8, 15, 14, 13, 12, 3, 2, 0, 7, 6, 5, 27, 26, 25, 4, 31, 30, 28, 19, 18, 17, 16, 23, 22, 21, 20, 43, 1, 40, 47, 46, 45, 44, 35, 33, 32, 39, 38, 37, 36, 58, 57, 56, 63, 62, 60, 51, 49, 48, 55, 53, 52, 75, 73, 72, 79, 77, 67, 66, 65, 71, 70, 68, 90, 89, 88, 95, 94, 93, 92, 83, 82, 81, 80, 87, 86, 84, 107, 106, 104 };
            
            //MEX = 1000
            //int[] values = new int[1000];
            //for (int i = 0; i < values.Length; i++) values[i] = i;
            
            //Импровизированный счетчик итераций
            int total = 0;
            int mex = GetMEX(values, ref total);
            Console.WriteLine($"mex: {mex}, total: {total}");
            Console.ReadKey();
        }

И еще один момент в статье я часто упоминаю слово «массив», хотя более правильным будет «множество», то заранее хочу извиниться перед теми, кому будет резать слух данное допущение.

Примечание 1 на основе комментариев: Многие придрались к O(n), мол все алгоритмы O(n) и по фигу, что «O» везде разное и не даёт фактически сравнить количество итераций. То для душевного спокойствия поменяем O на T. Где T более-менее понятная операция: проверка или присвоение. Так, как я понимаю, всем будет проще

Примечание 2 на основе комментариев: мы рассматриваем случай когда исходное множество НЕупорядоченное. Ибо сортировка это множества — тоже требует времени.

1) Решение в лоб

Как нам найти «минимальное отсутствующие число»? Самый простой вариант – сделать счетчик и перебирать массив до тех пор, пока не найдем число равное счетчику.

  static int GetMEX(int[] values, ref int total)
        {
            for (int mex = 0; mex < values.Length; mex++)
            {
                bool notFound = true;
                for (int i = 0; i < values.Length; i++)
                {
                    total++;
                    if (values[i] == mex)
                    {
                        notFound = false;
                        break;
                    }
                }
                if (notFound)
                {
                    return mex;
                }
            }
            return values.Length;
        }
    }

Максимально базовый случай. Сложность алгоритма составляет T(n*cell(n/2))… Т.к. для случая { 0, 1, 2, 3, 4 } нам нужно будет перебрать все числа т.к. совершить 15 операций. А для полностью заполного ряда из 100 числе 5050 операций… Так себе быстродейственность.

2) Просеивание

Второй по сложности вариант в реализации укладывается в T(n)… Ну или почти T(n), математики хитрят и не учитывают подготовку данных… Ибо, как минимум, — нам нужно знать максимальное число во множестве.

С точки зрения математики выглядит так.

Берется битовый массив S длинной m (где m – длина массива V) заполненный 0. И в один проход исходному множеству (V) в массиве (S) ставятся 1. После этого в один проход находим первое пустое значение. Все значения больше m можно просто игнорировать т.к. если в массиве «не хватает» значений до m, то явно будет меньше длины m.

static int GetMEX(int[] values, ref int total)
        {
            bool[] sieve = new bool[values.Length];
            for (int i = 0; i < values.Length; i++)
            {
                total++;
                var intdex = values[i];
                if (intdex < values.Length)
                {
                    sieve[intdex] = true;
                }
            }
            for (int i = 0; i < sieve.Length; i++)
            {
                total++;
                if (!sieve[i])
                {
                    return i;
                }
            }
            return values.Length;
        }

Т.к. «математики» – хитрые люди. То они говорят, что алгоритм T(n) ведь проход по исходному массиву всего один…

Вот сидят и радуются, что такой крутой алгоритм придумали, но правда такова.
Первое — нужно пройтись по исходному массиву и отметить это значение в массиве S T1(n)
Второе — нужно пройтись по массиву S и найти там первую попавшеюся свободную ячейку T2(n)
Итого, т.к. все операции в целом не сложные можно упростить все расчеты до T(n*2)

Но это явно лучше решения в лоб… Давайте проверим на наших тестовых данных:

1. Для случая { 0, 12, 4, 7, 1 }: В лоб: 11 итераций, просеивание: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: В лоб: 15 итераций, просеивание: 10 итераций
3. Для случая { 11,…}: В лоб: 441 итерация, просеивание: 108 итерация
4. Для случая { 0,…,999}: В лоб: 500500 итераций, просеивание: 2000 итераций

Дело в том, что если «отсутствующее значение» является небольшим числом, то в таком случае — решение в лоб оказывается быстрее, т.к. не требует тройного прохода по массиву. Но в целом, на больших размерностях явно проигрывает просеиванию, что собственно неудивительно.
С точки зрения «математика» – алгоритм готов, и он великолепен, но вот с точки зрения «программиста» – он ужасен из-за объема оперативной памяти, израсходованной впустую, да и финальный проход для поиска первого пустого значения явно хочется ускорить.

Давайте сделаем это, и оптимизируем код.

static int GetMEX(int[] values, ref int total)
        {
            var max = values.Length;
            var size = sizeof(ulong) * 8;
            ulong[] sieve = new ulong[(max / size) + 1];
            ulong one = 1;
            for (int i = 0; i < values.Length; i++)
            {
                total++;
                var intdex = values[i];
                if (intdex < values.Length)
                {
                    sieve[values[i] / size] |= (one << (values[i] % size));
                }
            }

            var maxInblock = ulong.MaxValue;
            for (int i = 0; i < sieve.Length; i++)
            {
                total++;
                if (sieve[i] != maxInblock)
                {
                    total--;
                    for (int j = 0; j < size; j++)
                    {
                        total++;
                        if ((sieve[i] & (one << j)) == 0)
                        {
                            return i * size + j;
                        }
                    }
                }
            }
            return values.Length;
        }

Что мы тут сделали. Во-первых, в 64 раза уменьшили количество оперативной памяти, которая необходима.

var size = sizeof(ulong) * 8;
ulong[] sieve = new ulong[(max / size) + 1];

Во-вторых, оптимизировали финальную проверку: мы проверяем сразу блок на вхождение первых 64 значений: if (sieve[i] != maxInblock) и как только убедились в том, что значение блока не равно бинарным 11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111, только тогда ищем уже вхождение на уровне блока: ((sieve[i] & (one << j)) == 0

В итоге алгоритм просеивание нам дает следующие результат:

1. Для случая { 0, 12, 4, 7, 1 }: просеивание: 8 итераций, просеивание с оптимизацией: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание: 10 итераций, просеивание с оптимизацией: 11 итераций
3. Для случая { 11,…}: просеивание: 108 итерация, просеивание с оптимизацией: 108 итерации
4. Для случая { 0,…,999}: просеивание: 2000 итераций, просеивание с оптимизацией: 1056 итераций

Так, что в итоге в теории по скорости?

T(n*3) мы превратили в T(n*2) + T(n / 64) в целом, чуть увеличили скорость, да еще объём оперативной памяти уменьшили аж в 64 раза. Что хорошо)

3) Сортировка

Как не сложно догадаться, самый простой способ найти отсутствующий элемент во множестве – это иметь отсортированное множество.

Самый быстрый алгоритм сортировки — это «quicksort» (быстрая сортировка), которая имеет сложность в T1(n log(n)). И итого мы получим теоретическую сложность для поиска MEX в T1(n log(n)) + T2(n)

static int GetMEX(int[] values, ref int total)
        {
            total = values.Length * (int)Math.Log(values.Length);
            values = values.OrderBy(x => x).ToArray();
            for (int i = 0; i < values.Length - 1; i++)
            {
                total++;
                if (values[i] + 1 != values[i + 1])
                {
                    return values[i] + 1;
                }
            }
            return values.Length;
        }

Шикарно. Ничего лишнего.

Проверим количество итераций

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка: ~7 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка: ~9 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка: ~356 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка: ~6999 итераций

Здесь указаны средние значения, и они не совсем справедливы. Но в целом: сортировка — не требует дополнительной памяти и явно позволяет упростить последний шаг в переборе.
Примечание: values.OrderBy(x => x).ToArray() – да я знаю, что тут выделилась память, но если делать по уму, то можно изменить массив, а не копировать его…


Вот у меня и возникла идея оптимизировать quicksort для поиска MEX. Данный вариант алгоритма я не находил в интернете, ни с точки зрения математики, и уж тем более с точки зрения программирования. То код будем писать с 0 по дороге придумывая как он будет выглядеть :D

Но, для начала, давайте вспомним как вообще работает quicksort. Я бы ссылку дал, но нормальное пояснение quicksort на пальцах фактически нет, создается ощущение, что авторы пособий сами разбираются в алгоритме пока его рассказывают про него…

Так вот, что такое quicksort:
У нас есть неупорядоченный массив { 0, 12, 4, 7, 1 }
Нам потребуется «случайное число», но лучше взять любое из массива, — это называется опорное число (T).

И два указателя: L1 – смотрит на первый элемент массива, L2 смотрит на последний элемент массива.

0, 12, 4, 7, 1
L1 = 0, L2 = 1, T = 1 (T взял тупа последние)

Первый этап итерации:
Пока работам только с указателем L1
Сдвигаем его по массиву вправо пока не найдем число больше чем наше опорное.
В нашем случае L1 равен 8

Второй этап итерации:
Теперь сдвигаем указатель L2
Сдвигаем его по массиву влево пока не найдем число меньше либо равное чем наше опорное.
В данном случае L2 равен 1. Т.к. я взял опорное число равным крайнему элементу массива, а туда же смотрел L2.

Третей этап итерации:
Меняем числа в указателях L1 и L2 местами, указатели не двигаем.
И переходим к первому этапу итерации.
Эти этапы мы повторяем до тех пор, пока указатели L1 и L2 не будет равны, не значения по ним, а именно указатели. Т.е. они должны указывать на один элемент.

После того как указатели сойдутся на каком-то элементе, обе части массива будут всё еще не отсортированы, но уже точно, с одной стороны «обединённых указателей (L1 и L2)» будут элементы, которые меньше T, а со второй больше T. Именно этот факт нам и позволяет разбить массив на две независимые группы, которые можно сортировать в разных потоках в дальнейших итерациях.

Статья на wiki, если и у меня непонятно написанно

Напишем Quicksort

static void Quicksort(int[] values, int l1, int l2, int t, ref int total)
        {
            var index = QuicksortSub(values, l1, l2, t, ref total);
            if (l1 < index)
            {
                Quicksort(values, l1, index - 1, values[index - 1], ref total);
            }
            if (index < l2)
            {
                Quicksort(values, index, l2, values[l2], ref total);
            }
        }

        static int QuicksortSub(int[] values, int l1, int l2, int t, ref int total)
        {
            for (; l1 < l2; l1++)
            {
                total++;
                if (t < values[l1])
                {
                    total--;
                    for (; l1 <= l2; l2--)
                    {
                        total++;
                        if (l1 == l2)
                        {
                            return l2;
                        }
                        if (values[l2] <= t)
                        {
                            values[l1] = values[l1] ^ values[l2];
                            values[l2] = values[l1] ^ values[l2];
                            values[l1] = values[l1] ^ values[l2];
                            break;
                        }
                    }
                }
            }
            return l2;
        }

Проверим реальное количество итераций:

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка: 11 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка: 14 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка: 1520 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка: 500499 итераций

Попробуем поразмышлять вот над чем. В массиве { 0, 4, 1, 2, 3 } нет недостающих элементов, а его длина равна 5. Т.е. получается, массив в котором нет отсутствующих элементов равен длине массива — 1. Т.е. m = { 0, 4, 1, 2, 3 }, Length(m) == Max(m) + 1. И самое главное в этом моменте, что это условие справедливо, если значения в массиве переставлены местами. И важно то, что это условие можно распространить на части массива. А именно вот так:
{ 0, 4, 1, 2, 3, 12, 10, 11, 14 } зная, что в левой части массива все числа меньше некого опорного числа, например 5, а в правой всё что больше, то нет смысла искать минимальное число слева.

Т.е. если мы точно знаем, что в одной из частей нет элементов больше определённого значения, то само это отсутствующие число нужно искать во второй части массива. В целом так работает алгоритм бинарного поиска.

В итоге у меня родилась мысль упростить quicksort для поиска MEX объединив его с бинарным поиском. Сразу скажу нам не нужно будет полностью отсортировывать весь массив только те части, в которых мы будем осуществлять поиск.

В итоге получаем код

static int GetMEX(int[] values, ref int total)
        {
            return QuicksortMEX(values, 0, values.Length - 1, values[values.Length - 1], ref total);
        }

        static int QuicksortMEX(int[] values, int l1, int l2, int t, ref int total)
        {
            if (l1 == l2)
            {
                return l1;
            }
            int max = -1;
            var index = QuicksortMEXSub(values, l1, l2, t, ref max, ref total);
            if (index < max + 1)
            {
                return QuicksortMEX(values, l1, index - 1, values[index - 1], ref total);
            }
            if (index == values.Length - 1)
            {
                return index + 1;
            }
            return QuicksortMEX(values, index, l2, values[l2], ref total);
        }

        static int QuicksortMEXSub(int[] values, int l1, int l2, int t, ref int max, ref int total)
        {
            for (; l1 < l2; l1++)
            {
                total++;
                if (values[l1] < t && max < values[l1])
                {
                    max = values[l1];
                }
                if (t < values[l1])
                {
                    total--;
                    for (; l1 <= l2; l2--)
                    {
                        total++;
                        if (values[l2] == t && max < values[l2])
                        {
                            max = values[l2];
                        }
                        if (l1 == l2)
                        {
                            return l2;
                        }
                        if (values[l2] <= t)
                        {
                            values[l1] = values[l1] ^ values[l2];
                            values[l2] = values[l1] ^ values[l2];
                            values[l1] = values[l1] ^ values[l2];
                            break;
                        }
                    }
                }
            }
            return l2;
        }

Проверим количество итераций

1. Для случая { 0, 12, 4, 7, 1 }: просеивание с оптимизацией: 8, сортировка MEX: 8 итераций
2. Для случая { 0, 1, 2, 3, 4 }: просеивание с оптимизацией: 11 итераций, сортировка MEX: 4 итераций
3. Для случая { 11,…}: просеивание с оптимизацией: 108 итерации, сортировка MEX: 1353 итераций
4. Для случая { 0,…,999}: просеивание с оптимизацией: 1056 итераций, сортировка MEX: 999 итераций

Итого

Мы получили разные варианты поиска MEX. Какой из них лучше — решать вам.

В целом. Мне больше всех нравится просеивание, и вот по каким причинам:
У него очень предсказуемое время выполнения. Более того, этот алгоритм можно легко использовать в многопоточном режиме. Т.е. разделить массив на части и каждую часть пробегать в отдельном потоке:

for (int i = minIndexThread; i < maxIndexThread; i++)
sieve[values[i] / size] |= (one << (values[i] % size));

Единственное, нужен lock при записи sieve[values[i] / size]. И еще — алгоритм идеален при выгрузке данных из базы данных. Можно грузить пачками по 1000 штук например, в каждом потоке и всё равно он будет работать.

Но если у нас строгая нехватка памяти, то сортировка MEX – явно выглядит лучше.

P.S.

Я начал рассказ с конкурса на OZON в котором я пробовал участвовать, сделав «предварительный вариант» алгоритма просеиванья, приз за него я так и не получил, OZON счел его неудовлетворительным… По каким именно причинам — он так и не сознался… Да и кода победителя я тоже не видел. Может у кого-то есть идеи как можно решить задачу поиска MEX лучше?