Компания SpaceX, основанная небезызвестным Илоном Маском, выпустила симулятор ручной стыковки корабля Crew Dragon с МКС. Если все пойдет по плану, стыковку проведут 27 мая 2020 года. Она будет проходить в полностью автоматическом режиме, но экипаж корабля сможет переключиться на ручное управление. Собственно, именно ручной режим и воспроизведен в симуляторе.

Сам симулятор расположен на сайте и представляет собой, довольно проблематичную, на первый взгряд игрушку…

Космический челнок так и норовит улететь не туда… А точность с которой нужно попасть в шлюз составляет 20 см… по трем осям, а также по угловой скорости, скорости смещения и т.д.

Во мне заиграли патриотичные чувства и как-то стало обидно, за бывшую космическую державу, и я принял этот симулятор как вызов. Раз Маск решил показать сложность стыковки, и какие сложности их инженеры проходили, чтобы сделать программу автоматической стыковки, я решил написать, в свободное от работы время, программу на JavaScript, которая с легкостью состыкует Dragon и МКС в этом симуляторе.

Как тебе такое, Илон Маск?


Курение вредит вашему здоровью

Внимание! Данный алгоритм является «стебным», и не предназначал для использования его в реальных условиях. Автор не несет ответственности за любые прямые или косвенные убытки, нанесенные вашему космическому кораблю или иным объектам при использовании данного алгоритма.

---

Для начала немного истории.

Широко известный факт, что наш многоразовый космический корабль «Буран» был очень похож на американский челнок. А так же известно, что он летал всего только один раз, в отличии от американских «аналогов». Но мало кто знает, что его единственный полет был беспилотным. Он сам взлетел, сам приземлился и все это он сделал в очень плохие погодные условия.

Американские Шатлы всегда приземлялись только в ручном режиме. Это было удивительно, принимая во внимание тот факт, что компьютеры раньше были не мощнее калькулятора. То, в теории, это не должно быть сложно, — подумал вчера вечером.

---

Но дайте перейдем к сути. Что представляет собой симулятор на сайте SpaceX.

На старте мы видим общую информацию, что отклонение по всем параметрам должно быть в пределах 0.2 метра (20 см). Учитывая размеры станции и корабля, это довольно серьезное ограничение.

Запускаем симулятор и видим.



Сверху, справа и снизу центральной окружности — угловое отклонение корабля по трем осям.
Зеленым — текущее значение.

Синие — скорость в секунду с которым оно изменяется.

Слева смещение относительно, шлюза в метрах. Скорости смещения нет…

Контролёры управления внизу экрана представляют собой кнопки с дублированием их на клавиатуре.

Вот с них и начнем разбор программы, как наименее интересных.

Схема клавиатурных кнопок.



Левый блок отвечает за смещение относительно шлюза, а вот правый за смещение относительно осей.

Пишем, или находим в сети, код который умеет эмулировать клавиатруные нажатие на document. В моем случае код выглядел так.

function simulateKey(keyCode, type, modifiers) {
    var evtName = (typeof (type) === "string") ? "key" + type : "keydown";
    var modifier = (typeof (modifiers) === "object") ? modifier : {};

    var event = document.createEvent("HTMLEvents");
    event.initEvent(evtName, true, false);
    event.keyCode = keyCode;

    for (var i in modifiers) {
        event[i] = modifiers[i];
    }
    document.dispatchEvent(event);
}

function keyPress(keyCode) {
    simulateKey(keyCode)
    setTimeout(() => simulateKey(keyCode, "up"), 15);
}

Запишем коды кнопок:

let _accelerator = 69;
let _brake = 81;
let _translateLeft = 65;
let _translateRigth = 68;
let _translateUp = 87;
let _translateDown = 83;

let _left = 37;
let _rigth = 39;
let _up = 38;
let _down = 40;

let _rollRigth = 105;
let _rollLeft = 103;

Любая система управления подразумевает работу в цикле. Сделаем его наиболее простым, с шагом в 200 миллисекунд. За одно организуем счетчик, он нам еще понадобится.

let index = 0;
function A() {

    index++;
    setTimeout(A, 200);
}

A();

Вернемся к структуре сайта.

Его интересной особенностью является, что МКС рисуется на канвасе, а вот информация о состоянии нашего космического корабля нарисованы обычной разметкой. Такое чувство, что разработчики сайта предполагали, что найдутся подобные энтузиасты, кто захочет «автоматизировать» игру и дали им такую возможность… А может разметкой, было сделать, тупо, проще.



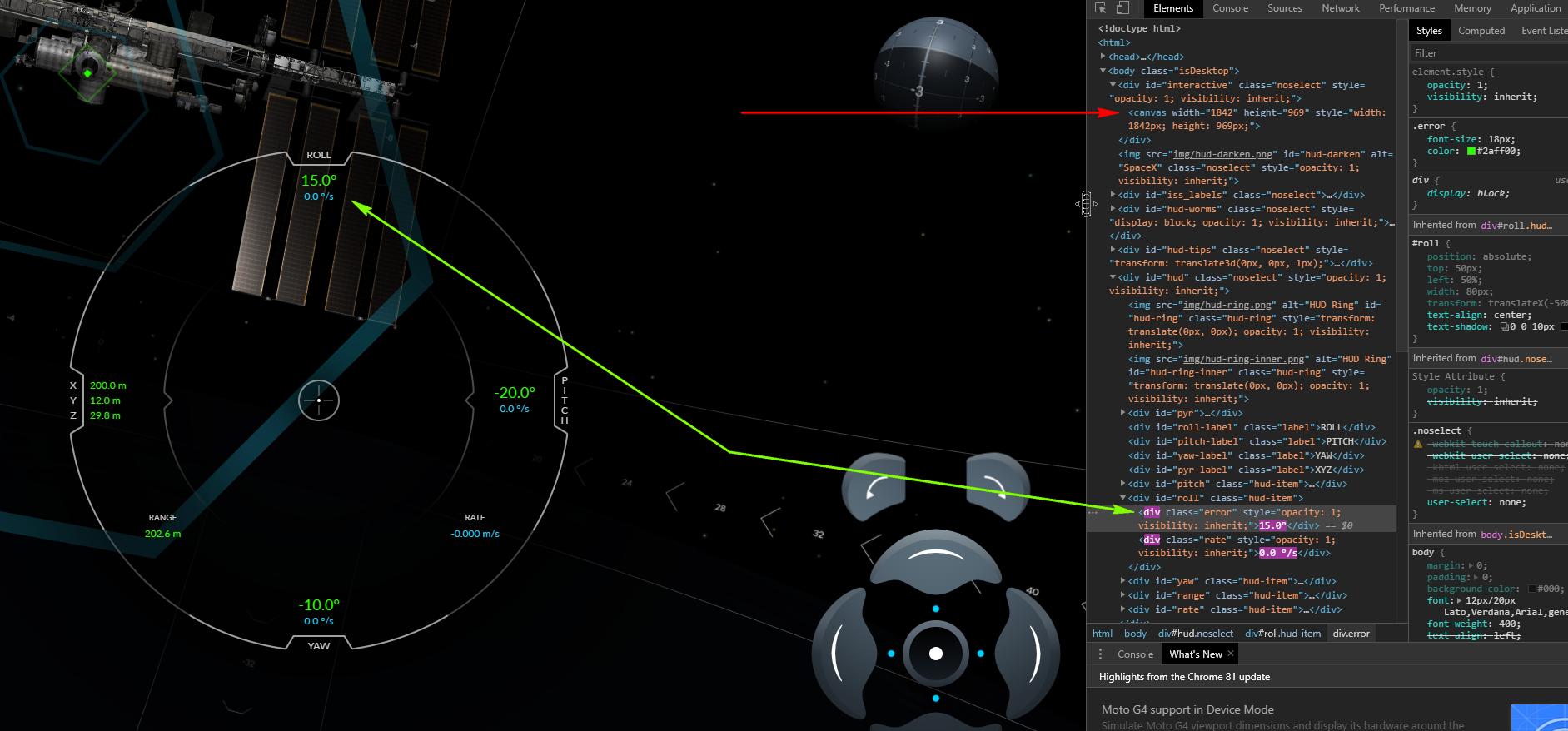
И так, допишем еще пару легких строк, дабы вытащить информацию о состоянии нашего космического аппарата.

    let range = parseFloat($("#range .rate").outerText.split(' '));

    let yDistance = parseFloat($("#y-range .distance").outerText.split(' ')[0]);
    let zDistance = parseFloat($("#z-range .distance").outerText.split(' ')[0]);

    let rollError = parseFloat($("#roll .error").outerText);
    let pitchError = parseFloat($("#pitch .error").outerText);
    let yawError = parseFloat($("#yaw .error").outerText);

    let rate = parseFloat($("#rate .rate").outerText.split(' ')[0]);

Как можно заметить я вытащил далеко не всё. Я вытащил только значения смещения, но скорость изменения значений брать не стал и вот почему…

На самом деле, это уже третья итерация алгоритма. Сначала он представляя собой простой вариант, который каждый 200 миллисекунд берет информацию о состоянии корабля и подгоняет его под 0.

Выглядело это так.

if (rollError !== -rollSpeed) {
        const rollLimit = (Math.abs(rollError) / 10);
        if (0 < rollError && rollSpeed < rollLimit) {
            keyPress(_rollRigth);
        } else if (rollError < -0 && -rollLimit < rollSpeed) {
            keyPress(_rollLeft);
        }
    }

И на самом деле он вполне был рабочий. Особенно для угловых смещений. А для смещения по осям я использовал такой вариант.

   const zLimit = (Math.abs(yawError) / 10);
        if (0 < zDistance && zSpeed < zLimit) {
            keyPress(_translateDown);
        } else if (zDistance < 0 && -1 < zSpeed) {
            keyPress(_translateUp);
        }

Скорость смещения корабля относительно каждой из осей на экран не выводится, но её не сложно подсчитать.

function carculateSpeed() {
    let yDistance = parseFloat($("#y-range .distance").outerText.split(' ')[0]);
    let zDistance = parseFloat($("#z-range .distance").outerText.split(' ')[0]);

    ySpeed = yPrev - yDistance;
    yPrev = yDistance;

    zSpeed = zPrev - zDistance;
    zPrev = zDistance;
    setTimeout(carculateSpeed, 1000);
}
carculateSpeed();

И получалось довольно сносно. Классическая схема управления с обратной связью. И пока корабль был на удалении от МКС мы летели себе вполне ровненько [так мне тогда казалось]. Но проблемы начинались возле самого корабля. На самом деле корабль сильно колбасило и попасть с точностью 0.2 метра было физически невозможно. Дело в том, что смешение нашего корабля происходило… скажем так в непрерывном пространстве (с большой точностью), а вот мы видели лишь десятые доли от этого. И естественно, пытаясь реагировать на них каждые 200 миллисекунд, у нас получалось очень сильные действия по регулированию. Мы слишком много раз «тыкали на кнопки» при малейшем отклонении. А чем ближе к кораблю, тем сильнее значения смещения начинали скакать и мы фактически еще больше раскачивали корабль… Увеличивая амплитуду его движения…

Нужно было где-то взять недостающую точность. Во второй итерации в решении данной задачи, я сам постарался посчитать уже только на основе смещения скорости. И да, так вроде тоже получалось неплохо, но это не решило проблему с движением…

А в чем суть проблемы движения? Ну смотрите, мы находим в космическом пространстве и нажимая на кнопки управление придаём ускорение кораблю в той или иной плоскости. Но как только мы отпускаем кнопку движение не прекращается. В космическом пространстве, в связи с вакуумом, нет никакого сопротивления. И как только мы придали импульс (нажатием кнопки) корабль начал движение с этой скоростью… И его нужно как-то остановить. Остановить в симуляторе довольно легко – нужно дать обратный импульс.

Но на второй итерации решения, увеличенная точность ошибки не давала мне ответа о том, как мне корректировать скорость…

И вот здесь нам и потребовался «циркуль». Капитан любого корабля/судна должен рассчитывать маршрут заранее. Если он даст команду сбросить скорость после того как войдет в порт, то вряд ли он ювелирно пришвартуется. А нам, как раз, это и нужно.

Нам нужно рассчитать маршрут, капитаны обычно это делают с помощью циркуля с дискретным состоянием его наконечников. И сделаем тоже самое. Будем рассчитывать маршрут на секунду вперед, которая будет включать в себя пять итераций нажатий на кнопки ну или не будет.

    if (index % 5 === 0) {
        calculatePath(roll, rollError);
        calculatePath(pitch, pitchError);
        calculatePath(yaw, yawError);
        calculatePath(y, yDistance);
        calculatePath(z, zDistance);
    }

Функция carculatePath, исходя их текущего значения отклонении, рассчитывает 5 шагов которые по идее должны это уклонение свести к 0. Необязательно на этой итерации, но каждый раз мы должны приближаться к заветному нулю в свой собственной более детальной сетке.

function calculatePath(data, value) {
    data.path = [];
    if (data.prev === value) {
        data.speed = 0;
    }
    for (let i = 0; i < 5; i++) {
        if (0 < value + data.speed * (i + 1)) {
            data.speed -= 0.1;
            data.path.push(-1);
        } else if (value + data.speed * (i + 1) < -0) {
            data.speed += 0.1;
            data.path.push(1);
        } else if (i > 0) {
            if (0 < data.speed) {
                data.speed -= 0.1;
                data.path.push(-1);
            } else if (data.speed < 0) {
                data.speed += 0.1;
                data.path.push(1);
            } else {
                data.path.push(0);
            }
        } else {
            data.path.push(0);
        }
    }
    data.prev = value;
}

Собственно всё, мы рассчитываем маршрут каждую «равную» секунду (index % 5 === 0) и теперь нужно просто идти этим курсом.

 let rollStep = roll.path[index % 5];
    if (0 < rollStep) {
        keyPress(_rollLeft);
    } else if (rollStep < 0) {
        keyPress(_rollRigth);
    }

    let pitchStep = pitch.path[index % 5];
    if (0 < pitchStep) {
        keyPress(_up);
    } else if (pitchStep < 0) {
        keyPress(_down);
    }

    let yawStep = yaw.path[index % 5];
    if (0 < yawStep) {
        keyPress(_left);
    } else if (yawStep < 0) {
        keyPress(_rigth);
    }

    let yStep = y.path[index % 5];
    if (0 < yStep) {
        keyPress(_translateRigth);
    } else if (yStep < 0) {
        keyPress(_translateLeft);
    }

    let zStep = z.path[index % 5];
    if (0 < zStep) {
        keyPress(_translateUp);
    } else if (zStep < 0) {
        keyPress(_translateDown);
    }

Единственный расчет, который уцелел еще с первой итерации, это сближение с кораблем.

Тут довольно всё, хорошо, мы, на относительно малом ходу, движемся вперед

    const rangeLimit = Math.min(Math.max((Math.abs(range) / 100), 0.05), 2);
    if (-rate < rangeLimit) {
        keyPress(_accelerator);
    } else if (-rangeLimit < -rate) {
        keyPress(_brake);
    }

Под спойлером полный код. Вы можете сами проверить его работоспособность на сайте iss-sim.spacex.com


Собственно всё. Всем спасибо за прочтение :)

P.S.

Да, я немного хайпанул и поприкалывался. Не воспринимайте статью всерьез, я просто хотел почувствовать себя космонавтом [или летуном космическим], как Гагарин Юрий Алексеевич… Хотя это скорее инженерная работа Королёва Сергея Павловича, который к сожалению, так и не побывал в космосе, о котором мечтал…