Всем привет! На Хабр есть несколько статей, в которых рассказывается об использовании модельно-ориентированного проектирования (МОП) при разработке различных систем, в том числе и системы управления электродвигателем.
Мне тоже захотелось попробовать этот подход в деле при том, что в лаборатории давно пылился отладочный комплект на базе микроконтроллера серии C2000 от Texas Instuments, да еще и с синхронным двигателем с постоянными магнитами (СДПМ) в придачу.
В этой и последующей статьях я хотел рассказать, как с помощью МОП я создал адекватную модель объекта управления (трехфазного двигателя), промоделировал алгоритм векторного управления, настроил регуляторы и автоматически сгенерировал код для микроконтроллера из модели.
Создание модели системы управления
В первую очередь я отправился в документацию MATLAB, чтобы найти уже работающие демонстрационные примеры, на которые можно опираться. Действительно такие имеются. Специально под задачи управления электродвигателями и для оптимизированной автоматической генерации кода была создана библиотека Motor Control Blockset. В описании к этой библиотеке также имеется теоретический минимум по способам управления трехфазными двигателями. Отлично – есть с чего начать.
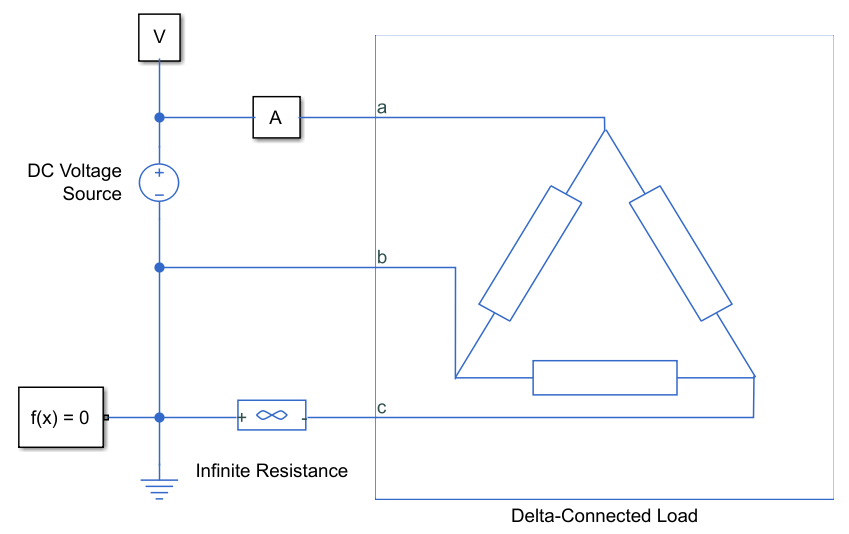
Оказалось, что даже есть готовый пример с реализацией векторного управления. Но обратив внимание на то, как моделируется сам двигатель, возникла проблема: в имеющимся у нас в распоряжении двигателе фазные обмотки соединены по схеме «треугольник», а рассматриваемой библиотеке не оказалось блока, описывающего поведение подобного двигателя. Пришлось задействовать блоки из библиотеки Simscape Electrical.
Также субъективно мне не понравилось, как выглядит модель, поэтому я решил создать новую модель, используя этот пример.
Я не хочу останавливаться на принципе работы векторного управления, из каких функциональных блоков он состоит и т.д. На Хабре есть хорошая статья, объясняющая эту тему «на пальцах».
Давайте сразу перейдем к модели.

Модель состоит из нескольких блоков:
PMSM with Encoder – модель СДПМ с инкрементальным энкодером.
Inverter with Current Sensors – модель инвертора с датчиками тока.
Phase Currents Computation – преобразование цифровых сигналов от датчиков тока в физические сигналы тока.
Position and Speed Computation – обработка сигналов от инкрементального энкодера.
Current Loop – токовый (внутренний) контур управления.
Speed Loop – скоростной (внешний) контур управления.
Кратко пройдемся по этим блокам.
Подсистема PMSM with Encoder включает уже упомянутый блок самого двигателя с учетом влияния трения и примитивная модель энкодера, представленная просто коэффициентом усиления (количество меток на диске * количество сформированных импульсов на метку). Сигнал полного оборота энкодера моделируется просто источником единичного сигнала ChangeFlag, время перехода из нулевого на единичный (т.е. выдачу энкодером импульса полного оборота) уровень можно выставлять самому. Также в сигнал обратной связи включена задержка Delay, которая составляет 10 тактов работы микроконтроллера.

В подсистеме Inverter with Current Sensors находятся блок Average-Value Inverter, на выходе которого получается усредненное значение выходного напряжения трехстоечного инвертора; блок М, в котором расположены идеальные датчики тока и подсистема Convert Currents, в которой сигналы с датчиков тока преобразуются в уровни АЦП с учетом его смещения. Здесь также учитывается задержка на преобразование сигналов АЦП.

В подсистеме Phase Currents Computation выполняются обратные преобразования: уровни АЦП преобразовываются в физические сигналы тока.

В подсистеме Position and Speed Computation на основе сигналов от энкодера вычисляются скорость и положение ротора двигателя. А также из механического положения ротора вычисляется электрическое. В блоке Quadrature Decoder находится алгоритм расчета положения ротора на основе счетчика положения, в него вводятся количество меток на диске энкодера, количество импульсов на метку и разрядность счетчика положения. Измерение скорости реализовано как разница между двумя положениями за определенный период времени.

Все тригонометрические преобразования, регуляторы токового контура и генератор ШИМ расположены с подсистеме Current Loop. Как в токовом контуре (контуры d- и q-компонент тока), так и в скоростном, я использовал ПИ-регуляторы с функцией борьбы с интегральным насыщением.

Стоит отметить, что вычисления синуса и косинуса угла между d-осью и вектором потокосцепления ротора вычисляется таблично, и в блоке Sine-Cosine Lookup можно задать количество элементов таблицы в зависимости от требуемой точности. Такой алгоритм вычисления тригонометрических функций является более оптимальным для реализации на микроконтроллере.
Для генерации ШИМ я выбрал схему SVPWM, хотя можно было поставить и обычную синусоидальную схему формирования, но после прочтения этой статьи мне захотелось посмотреть, что такое SVPWM и попробовать его в действии.
Регулятор скоростного контура находится в подсистеме Speed Loop.

Коэффициент усиления интегральной части в выбранных блоках ПИ-регуляторов из библиотеки Motor Control Blockset необходимо умножать на период дискретизации того контура, в котором он работает.
Модель учитывает частоты дискретизации контуров: контур тока работает на 20 кГц, а контур скорости на 2 кГц. Часть модели с объектом управления и инвертором может рассчитываться с каким угодно шагом интегрирования, главное, что наш алгоритм всегда будет работать на выбранных частотах дискретизации.
Что касается двигателя, то пока я взял параметры из документации, чтобы просто проверить работоспособность всей модели. Я использую двигатель BLY171D-24V-4000 компании Anaheim Automation. Документацию на него можно посмотреть здесь.
Еще важный момент, надо хоть как-то настроить регуляторы. На данном этапе подойдет просто ручной подбор.
Отключаю контур скорости и подаю на вход контура тока ступенчатый сигнал. Для d-компоненты уставка равна нулю, а для q-компоненты – 0.1 А. Вот что получилось для контура тока.

Далее подбираем параметры регулятора контура скорости, чтобы нас удовлетворял переходный процесс.

Мы убедились, что созданная модель работает. Следующий шаг – ввести в нее достоверные параметры двигателя.
Определение параметров двигателя
В примерах библиотеки Motor Control Blockset есть специальная модель, в которой реализованы алгоритмы определения параметров двигателя. Но она работает только на конкретных высокопроизводительных микроконтроллерах. Мой микроконтроллер оказался не таким производительным, и предложенная программа на нем не заработала. Поэтому пришлось выкручиваться и воспроизвести все эксперименты по параметризации двигателя самому. Благо в том же MATLAB и в предоставляемых им ресурсах оказались все необходимые материалы.
Лично я использовал эти статью и лекцию, чтобы вспомнить некоторые моменты про то, как ставить эксперименты для определения различных параметров, про которые нам когда-то рассказывали в институте, и даже узнать что-то новое. Лектор (он же и автор статьи) рассказывает очень доступно, правда на английском языке, и раскладывает все по полочкам, так что я только вкратце расскажу про эти эксперименты.
Также хорошим подспорьем может стать вот этот пример из документации, где на маленьких моделях показывается, как провести тот или иной эксперимент.
Сопротивление и индуктивность фазных обмоток
При определении сопротивления и индуктивности фазных обмоток нам поможет тот факт, что изменение тока в обмотке при подаче напряжения можно описать апериодическим звеном. Нам нужно подать напряжение на одну фазу, отключив от источника питания остальные две фазы. Используя мостовой трехстоечный инвертор, это просто реализовать.
Мы формируем контур протекания тока так, чтобы ток втекал в точку А и вытекал из точки В. При этом в точку С не должен поступать ток. Таким образом, на всем периоде работы должны быть включены ключи АН (верхний ключ стойки, подключенной к точке А) и BL (нижний ключ стойки, подключенной к точке В). И измеряем ток фазы А и постоянное напряжение питания.
Вот, что получилось на осциллографе (когда я перенес и обработал результаты в MATLAB).

На рисунке явно проглядывается линия, соответствующая апериодическому переходному процессу. Зашумленность результатов связана с тем, что я управлял ключами с помощью ШИМ, и мне не хотелось подавать все напряжение питания на фазу, поэтому я ограничился коэффициентом заполнения 10%.
Теперь предстояло отфильтровать сигналы, чтобы получить четкие значения, которые можно было бы использовать для численных расчетов. Я использовал медианный фильтр большого порядка.

Теперь мы знаем установившееся значение тока фазы и точное значение напряжения питания – можем найти сопротивление обмотки. Оно вычисляется по формуле: R = 1.5*0.1*Uпит/ia. Коэффициент 1.5 учитывает схему соединения фазных обмоток (напомню, у нас «треугольник»), поскольку в соединении «треугольник» при подобной коммутации ключей ток будет протекать по двум параллельным цепям, образованным из фазной обмотки А и двух фазных обмоток В и С, включенных последовательно. Коэффициент 0.1 – это коэффициент заполнения ШИМ.
Далее находим значение тока, которое равно 0.632*Iуст и определяем момент времени, в который ток принимает данное значение. Этот момент есть электромагнитная постоянная времени Та. Зная ее, определяем индуктивность L.
Теперь проверим с помощью модели эксперимента, правильно ли мы нашли все параметры. Модель выглядит вот так.
В результате моделирования получим

Результаты моделирования хорошо ложатся на экспериментальные данные.
Коэффициент противо-ЭДС
Для определения коэффициента противо-ЭДС нам потребуется еще один двигатель, который смог бы разогнать наш двигатель до нужной скорости. Я использовал для этой цели хороший шуруповёрт, который может держать постоянную скорость в течение всей продолжительности эксперимента.
Разогнав двигатель, я снимаю с него фазное напряжение и фильтрую его. Коэффициент вычисляется по формуле: Ce = Epeak/Vref. И наконец проверяю получившееся значение на модели эксперимента.

И получаю совпадение экспериментальных данных и моделирования.

Коэффициенты трения
Самый сложный эксперимент – это эксперимент по определению коэффициентов вязкого и сухого трения, поскольку он требует применения векторного управления для определения развиваемого двигателем момента на основе вычисленных значений q-компоненты тока. Напомню, что для СДПМ с неявнополюсным ротором компоненты индуктивностей по осям d и q равны (Lq = Lq), и поэтому сложная формула механического момента для этого двигателя
Mдв = (3/2)*P*[λpm*iq + (Ld − Lq)*id*iq]
превращается в простую линейную:
Mдв = (3/2)*P*λpm*iq = Се*iq.
Суть эксперимента в следующем. Мы определяем значения q-компоненты тока при различных скоростях вращения ротора. В результате мы имеем несколько точек, которые аппроксимируем линейной функцией y = B*x + J0, где J0 – коэффициент сухого трения (момент, требуемый для страгивания ротора) и B – коэффициент вязкого трения. В скобках указано расхождение в процентах аппроксимированных функций при моделировании и эксперименте, оно составляет менее 1%.

Момент инерции ротора
Момент инерции определяется «на выбеге» ротора, когда мы разгоняем ненагруженный двигатель, в определенный момент времени отключаем все фазы и ротор останавливается. Мы должны изучить именно процесс изменения скорости ротора от времени в течение процесса остановки. Оказывается, что он описывается экспоненциальной функцией:
ωr = (ωr0 + J0/В)*e−(В/J)*t − (J0/В).
Она получается из второго закона Ньютона, записанного для вращения ротора, при нулевых электромагнитном моменте и моменте нагрузки.
Определив скорость в этом процессе и зная коэффициенты трения и уравнение, которым мы будем аппроксимировать процесс, можно подобрать момент инерции. Для этого в MATLAB есть специализированный инструмент с графическим интерфейсом пользователя Curve Fitting, но я решил проделать все операции с помощью команд MATLAB.
Аппроксимация с помощью команд
% Задаем вид аппроксимационной функции (экспоненциальная функция)
myfittype = fittype(...
'(a+c)*exp(-b*x)-c',
'independent', 'x',
'dependent', 'y', ...
'coefficients',{'a','b','c'});
% Аппроксимирую экспериментальную кривую с начальными приближениями:
% a = RefSpeed = 400 рад/с - начальная скорость в эксперименте
% b = motor.B/J (B - коэффициент вязкого трения)
% c = motor.J0/motor.B (J0 - коэффициент сухого трения)
% J = 2.4e-6 кг*м^2 - момент инерции, взятый из документации
myfit = fit(...
double(timeLinearPart)',
double(speedLinearPart)',
myfittype,
'StartPoint', [RefSpeed motor.B/J motor.J0/motor.B]);
% Вывожу коэффициенты аппроксимационной функции
fitCoeffs = coeffvalues(myfit);
% Определяю истинный момент инерции
estimatedInertia = motor.B/fitCoeffs(2);После оценки этого параметра я подставил его в эту модель.

И получил отличный результат.

Заключение
Мы посмотрели, как создать модель векторного управления СДПМ с подсистемами обработки датчиков обратной связи, учитывающую работу контуров управления на разных частотах дискретизации.
Также экспериментально определили параметры нашего двигателя и помощью возможностей программы MATLAB/Simulink подтвердили на моделях эксперимента правильность найденных значений.
В следующей статье мы рассмотрим, как можно настроить регуляторы контуров, и перейдем к самому интересному: заработают ли программа, сгенерированная из модели, для микроконтроллера, и будет ли она работать так же, как и модель.

