Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Наивный алгоритм
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
static BigInteger FactNaive(int n)
{
BigInteger r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
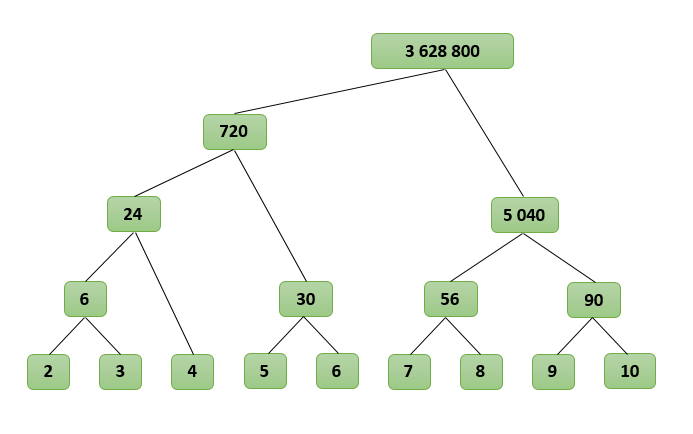
Реализуем описанный алгоритм:
static BigInteger ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (BigInteger)l * r;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
static BigInteger FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K2-ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K2. Аналогично для K3, K4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K2 + N / K3 + N / K4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (22), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (23), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (24) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 28 * 34 * 52 * 71 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
static BigInteger FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
bool[] u = new bool[n + 1]; // маркеры для решета Эратосфена
List<Tuple<int, int>> p = new List<Tuple<int, int>>(); // множители и их показатели степеней
for (int i = 2; i <= n; ++i)
if (!u[i]) // если i - очередное простое число
{
// считаем показатель степени в разложении
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
// запоминаем множитель и его показатель степени
p.Add(new Tuple<int, int>(i, c));
// просеиваем составные числа через решето
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
// вычисляем факториал
BigInteger r = 1;
for (int i = p.Count() - 1; i >= 0; --i)
r *= BigInteger.Pow(p[i].Item1, p[i].Item2);
return r;
}
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Библиотека GMP
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Сравнение производительности
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
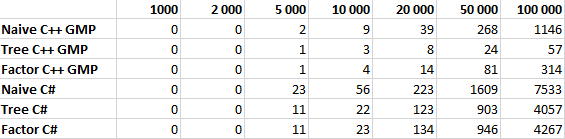
График с линейной шкалой
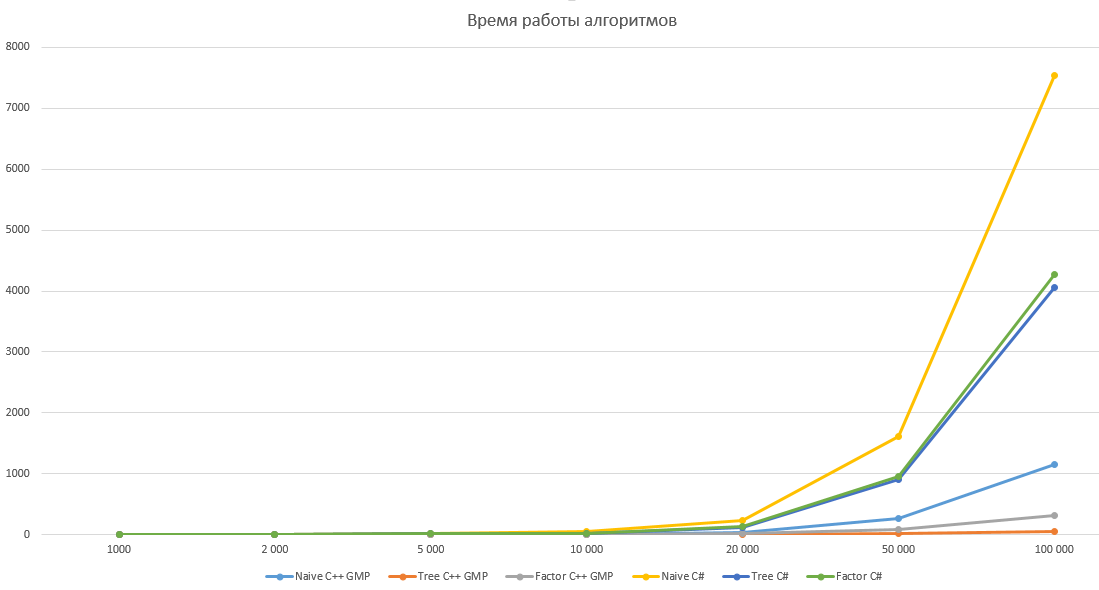
График с логарифмической шкалой
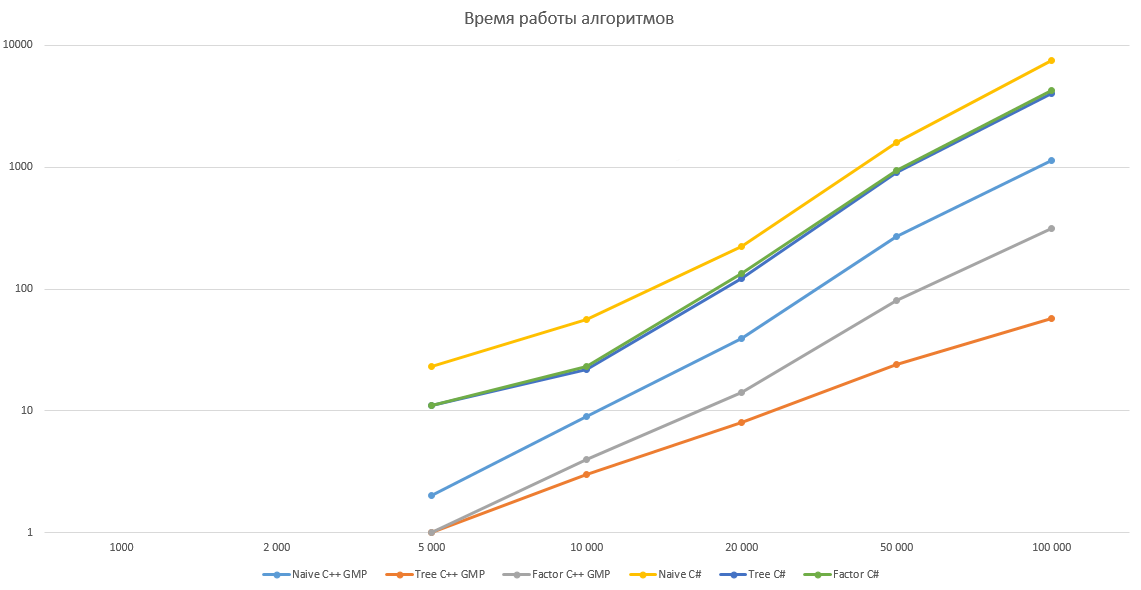
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
lany распараллелил дерево на Java с помощью Stream API и получил ускорение в 18 раз
Mrrl предложил оптимизацию факторизации на 15-20%
PsyHaSTe предложил улучшение наивной реализации
Krypt предложил распараллеленную версию на C#
SemenovVV предложил реализацию на Go
pomme предложил использовать GMP
ShashkovS предложил быстрый алгоритм на Python
Исходные коды
Исходные коды реализованных алгоритмов приведены под спойлерами
using System;
using System.Linq;
using System.Text;
using System.Numerics;
using System.Collections.Generic;
using System.Collections.Specialized;
namespace BigInt
{
class Program
{
static BigInteger FactNaive(int n)
{
BigInteger r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
static BigInteger ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (BigInteger)l * r;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
static BigInteger FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
static BigInteger FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
bool[] u = new bool[n + 1];
List<Tuple<int, int>> p = new List<Tuple<int, int>>();
for (int i = 2; i <= n; ++i)
if (!u[i])
{
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
p.Add(new Tuple<int, int>(i, c));
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
BigInteger r = 1;
for (int i = p.Count() - 1; i >= 0; --i)
r *= BigInteger.Pow(p[i].Item1, p[i].Item2);
return r;
}
static void Main(string[] args)
{
int n;
int t;
Console.Write("n = ");
n = Convert.ToInt32(Console.ReadLine());
t = Environment.TickCount;
BigInteger fn = FactNaive(n);
Console.WriteLine("Naive time: {0} ms", Environment.TickCount - t);
t = Environment.TickCount;
BigInteger ft = FactTree(n);
Console.WriteLine("Tree time: {0} ms", Environment.TickCount - t);
t = Environment.TickCount;
BigInteger ff = FactFactor(n);
Console.WriteLine("Factor time: {0} ms", Environment.TickCount - t);
Console.WriteLine("Check: {0}", fn == ft && ft == ff ? "ok" : "fail");
}
}
}
#include <iostream>
#include <ctime>
#include <vector>
#include <utility>
#include <gmpxx.h>
using namespace std;
mpz_class FactNaive(int n)
{
mpz_class r = 1;
for (int i = 2; i <= n; ++i)
r *= i;
return r;
}
mpz_class ProdTree(int l, int r)
{
if (l > r)
return 1;
if (l == r)
return l;
if (r - l == 1)
return (mpz_class)r * l;
int m = (l + r) / 2;
return ProdTree(l, m) * ProdTree(m + 1, r);
}
mpz_class FactTree(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
return ProdTree(2, n);
}
mpz_class FactFactor(int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
vector<bool> u(n + 1, false);
vector<pair<int, int> > p;
for (int i = 2; i <= n; ++i)
if (!u[i])
{
int k = n / i;
int c = 0;
while (k > 0)
{
c += k;
k /= i;
}
p.push_back(make_pair(i, c));
int j = 2;
while (i * j <= n)
{
u[i * j] = true;
++j;
}
}
mpz_class r = 1;
for (int i = p.size() - 1; i >= 0; --i)
{
mpz_class w;
mpz_pow_ui(w.get_mpz_t(), mpz_class(p[i].first).get_mpz_t(), p[i].second);
r *= w;
}
return r;
}
mpz_class FactNative(int n)
{
mpz_class r;
mpz_fac_ui(r.get_mpz_t(), n);
return r;
}
int main()
{
int n;
unsigned int t;
cout << "n = ";
cin >> n;
t = clock();
mpz_class fn = FactNaive(n);
cout << "Naive: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class ft = FactTree(n);
cout << "Tree: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class ff = FactFactor(n);
cout << "Factor: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
t = clock();
mpz_class fz = FactNative(n);
cout << "Native: " << (clock() - t) * 1000 / CLOCKS_PER_SEC << " ms" << endl;
cout << "Check: " << (fn == ft && ft == ff && ff == fz ? "ok" : "fail") << endl;
return 0;
}
Комментарии (38)

Mrrl
14.04.2015 21:21+6Интересная задача. Как-то так можно выиграть ещё 15-20%:
static BigInteger FactFast(int n) { int p=0,c=0; while((n >> p) > 1) { p++; c += n >> p; } BigInteger r=1; int k=1; for(;p>=0;p--){ int n1=n >> p; BigInteger x=1; int a=1; for(;k<=n1;k+=2){ if((long)a*k < int.MaxValue) a*=k; else{ x*=a; a=k; } } r*=BigInteger.Pow(x*a,p+1); } return r << c; }
Там для каждого нечётного k считается наибольшее p, для которого k*2^p <= n, перемножаются все k, для которых p одинаковы, и произведение возводится в степень p+1. Потом всё это перемножается, и в конце умножается на нужную степень двойки (показатель равен n/2+n/4+n/8+....)
5nw Автор
16.04.2015 16:34Ценное замечание, спасибо
У меня еще была мысль вычислять n! как n! = ((n / 2)!)2 * d, где d — множители, потерянные при целочисленном делении, но до алгоритма дело не дошло
Mrrl
16.04.2015 17:08Самым быстрым способом без перехода к быстрым алгоритмам умножения мне кажется такой:
— Берётся FactFactor
— перемножаются все простые числа, которые надо возводить в одну и ту же степень
— каждое из этих произведений возводится в нужную степень
— и результаты перемножаются.
При этом получается меньше всего повторных умножений, дающих длинные результаты (если A и B — числа длины N, то на подсчёт (A*B)^4 мы затратим 21*N^2 операций, а на A^4*B^4 — 26*N^2)
Правда, на 50000! я выигрыша не увидел, но на 100000! он составил уже около 2%.

iroln
14.04.2015 22:34+3Кстати в Python 3.x из коробки используется быстрый алгоритм, тогда как в Python 2.x был наивный. Прирост производительности примерно в 14 раз.
stackoverflow.com/questions/9815252/why-is-math-factorial-much-slower-in-python-2-x-than-3-x
В абсолютных значениях в Python3 факториал от 50000 на стареньком Q6600 считается за ~97 мс.

PsyHaSTe
14.04.2015 22:36+4Слегка оттюнинговал наивную реализацию, она чуть медленнее на х86, чем ваше решение с деревом, зато на х64 немного быстрее его
static BigInteger FactNaiveTuned(int n) { if (n <= 1) return 1; BigInteger r1 = 1, r2 = 1, r3 = 1, r4 = 1; int i; for (i = n; i > 4; i -= 4) { r1 *= i; r2 *= i - 1; r3 *= i - 2; r4 *= i - 3; } int mult = i == 4 ? 24 : i == 3 ? 6 : i == 2 ? 2 : 1; return (r1*r2)*(r3*r4)*mult; }

Sqwony
14.04.2015 22:48+3С деревом множителей хорошо придумано, я бы добавил к нему использование многопоточности. Учитывая архитектуру — он это все будет последовательно умножать используя одно ядро. Исходя из количества ядер на машине, можно ускорить этот процесс путем раскидывания дерева умножения на разные ядра процессора.

Krypt
15.04.2015 00:51Поэкспериментировал с многопоточностью:
const int threadCount = 2; static Task<BigInteger> AsyncProdTree(int l, int r) { return Task<BigInteger>.Run(() => ProdTree(l, r)); } static BigInteger FactThreadingTree(int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; if (n < threadCount+1) return ProdTree(2, n); Task<BigInteger>[] tasks = new Task<BigInteger>[threadCount]; tasks[0] = AsyncProdTree(2, n / threadCount); for (int i = 1; i < threadCount; i++) { tasks[i] = AsyncProdTree(((n / threadCount) * i) + 1, (n / threadCount) * (i + 1)); } Task<BigInteger>.WaitAll(tasks); BigInteger result = 1; for (int i = 0; i < threadCount; i++) { result *= tasks[i].Result; } return result; }
FactNaive: 2.2
FactTree: 1.1
FactFactor: 1.1
FactThreadingTree: 0.9
Krypt
15.04.2015 00:57+1Почему-то подсветка синтаксиса не работает.
_https://gist.github.com/krypt-lynx/4326359b748c5f4b9cc8

Krypt
15.04.2015 01:52Насколько я вижу, всё опирается в последнюю операцию умножения:
2-25000: 00:00:00.2458574
25001-50000: 00:00:00.3246583
finalizing: 00:00:00.5395141
total: 00:00:00.8882113
И быстрее 0.54 получить не получится ну никак.

u_story
14.04.2015 23:56+1Возможно, мое решение покажется немного странным, но мы делали так:
1. Считаешь факториал до предельного числа и записываешь данные в файл.
2. Из файла переносишь данные в массив в коде программы, и по когда нужно значение факториала, просто выводить значение массива, на нужно позиции.
Скорость не засекал.
ivlis
15.04.2015 04:00+2Так обычно делают, когда надо считать нетривиальные функции на слабом железе. Пишут таблицы синусов, логарифмов и прочего.

toxicdream
15.04.2015 08:40+10Вспомнились «трудное детство без калькулятора» и потрепанная книжка «4-значные таблицы Брадиса» :(

Sykoku
15.04.2015 13:05+1Сначала они были таблицами Хренова (как их называли можете сами догадаться). И талмуд сей был толще и тяжелее.

lany
15.04.2015 12:27+1Факториал 50000 содержит больше 200000 десятичных цифр. Если нужны любые точные значения факториалов от 1 до 50000, то вам потребуется не меньше гигабайта памяти. Вычитка в массив тоже может занять существенное время.

asArtem
15.04.2015 18:08вычитка из одномерного массива занимает время О(1) при обращении по индексу. Даже когда у вас закончатся разрядность double и придётся читать цифры из строк спец. массива, то все равно там будет использоваться индекс и время доступа будет О(1).
Подобный пример, кажется у кнута был с поиском номеров телефонов за очень быстрое время. Где номер ячейки памяти был равен номеру телефона. Создавая по такому принципу все будет ок.
lany
16.04.2015 04:52Я про вычитку из файла в массив. Ну и не забывайте про своп. Это теоретикам программирования кажется, что обращение к любой ячейке памяти занимает одинаковое время, а тут page fault и приплыли.

Dima_Amigo
15.04.2015 11:30+1

REZ1DENT3
15.04.2015 14:14хоть на паскале… На втором курсе нам нужно было вычислить 15000! на ассемблере, это была моя первая программа на TASM

SemenovVV
15.04.2015 15:08+1у меня получилось примерно в 2 раза снизить время вычисления факториала, по сравнению с базовым вариантом.
Идея проста, в цикле с шагом 2 считаем произведения i * (i+1) в обычной арифметике, а потом в длинной арифметике добавляем произведение к результату.Пример факториалов на golang// factorial project main.go
package main
import (
«fmt»
«math/big»
«os»
«strconv»
«time»
)
func main() {
fmt.Print(«введите N >»)
bufer := make([]byte, 80)
length, err := os.Stdin.Read(bufer)
if err != nil {
os.Exit(1)
}
razmern, err := strconv.Atoi(string(bufer[:length-2]))
if err != nil {
os.Exit(2)
}
MMM := int32(razmern)
factor1(MMM)
factor2(MMM)
}
func factor1(NN int32) {
var ii int32
rez := big.NewInt(1)
START := time.Now()
for ii = 2; ii <= NN; ii++ {
temp := new(big.Int)
temp.Mul(rez, big.NewInt(int64(ii)))
rez = temp
}
fmt.Printf(«время расчета %v сек\n», time.Since(START).Seconds())
//fmt.Println(«N=», NN, " N!=", rez)
return
}
func factor2(NN int32) {
// только для четных NN
var ii int64
var wsp int64
rez := big.NewInt(2)
START := time.Now()
for ii = 3; ii <= int64(NN); ii = ii + 2 {
wsp = ii * (ii + 1)
temp := new(big.Int)
temp.Mul(rez, big.NewInt(int64(wsp)))
rez = temp
}
fmt.Printf(«время расчета %v сек\n», time.Since(START).Seconds())
//fmt.Println(«N=», NN, " N!=", rez)
return
}
pomme
15.04.2015 15:12+2www.cs.berkeley.edu/~fateman/papers/factorial.pdf — статья 2006 года, имейте это в виду, сравнивая время работы.
The time to compute 20,000! using gmaxfact or gkg and pentium-4 (Пентиум-4, Карл!) GMP arithmetic is about 0.021 seconds.
А если применить разложение на простые множители, получится 15 мс: By intertwining a prime-number sieve with the computation, we can beat the split-recursive idea as embodied in programs kg and gkg also using GMP, by about 25 percent, for numbers of the size of 20,000!..
Основной вывод — используйте GMP. И вот почему: A simple profiling of factorial of 20,000 shows that most of these algorithms use 98 percent or more of their time in bignumber multiplication.
5nw Автор
16.04.2015 16:19Ценное замечание, спасибо.
Сейчас попробовал C++ и GMP, получил такие результаты:
n = 50000
Naive: 271 ms
Tree: 23 ms
Factor: 81 ms
Check: ok
Получается, у Майкрософта квадратичное умножение, но довольно странно оптимизированное для умножения на «короткое число» (которое помещается в одну «ячейку» длинного). Наверное добавлю этот момент в статью.

Idot
15.04.2015 18:11Удивительно, что никто не вспомнил, что современный процессор обычно имеет четыре ядра. Что означает то, что желающим посчитать максимально быстро, стоит разбить вычисления на четыре параллельных потока.

denismaster
15.04.2015 18:59Разбить последовательность от 1 до N на четыре подпоследовательности, в каждом потоке вычислить произведение множителей в подпоследовательности, а потом просто умножить 4 числа?

Sqwony
15.04.2015 21:37Я об этом уже писал выше, про то что можно использовать несколько ядер процессора

5nw Автор
16.04.2015 16:07Меня в первую очередь интересовала именно алгоритмическая оптимизация, а распараллеливание это все таки больше оптимизация техническая, ориентированная на конкретное устройство — многоядерный процессор. Хотя, конечно, дерево само напрашивается на распараллеливание :)

ShashkovS
16.04.2015 20:07+1Реализация на Python версии, объединяющей обе идеи, работает у меня всего 0.45с, итоговое ускорение по сравнению с наивной версией в 8 раз. Всего в 5-6 раз медленнее C++ и GMP. Круто.
Код на Pythonfrom timeit import timeit def naive_factorial(n): res = 1 for i in range(2, n + 1): res *= i return res def bin_pow_factorial(n): def eratosthenes(N): simp = [2] nonsimp = set() for i in range(3, N + 1, 2): if i not in nonsimp: nonsimp |= {j for j in range(i * i, N + 1, 2 * i)} simp.append(i) return simp def calc_pow_in_factorial(a, b): res = 0 while a: a //= b res += a return res fact_pows = [(x, calc_pow_in_factorial(n, x)) for x in reversed(eratosthenes(n+1))] if len(fact_pows) % 2 == 1: fact_pows.append((1, 1)) mul = [fact_pows[i][0] ** fact_pows[i][1] * fact_pows[-i-1][0] ** fact_pows[-i-1][1] for i in range(len(fact_pows)//2)] while len(mul) > 1: if len(mul) % 2 == 1: mul.append(1) mul = [mul[i] * mul[-i-1] for i in range(len(mul)//2)] return mul[0] N = 50000 REPEATS = 10 setup = 'from __main__ import N, naive_factorial, bin_pow_factorial' print(timeit(stmt = 'naive_factorial(N)', setup=setup, number=REPEATS)/REPEATS) print(timeit(stmt = 'bin_pow_factorial(N)', setup=setup, number=REPEATS)/REPEATS) >>> 3.6880629397247233 0.45309165938008744
OsipovRoman
19.04.2015 16:37+1В Wolfram Language для вычисления n! используется, скажем, алгоритм на основе метода умножения Шёнхаге—Штрассена, основанный на динамической декомпозиции на простые множители и их степени.
Результат тестирования функции Factorial:

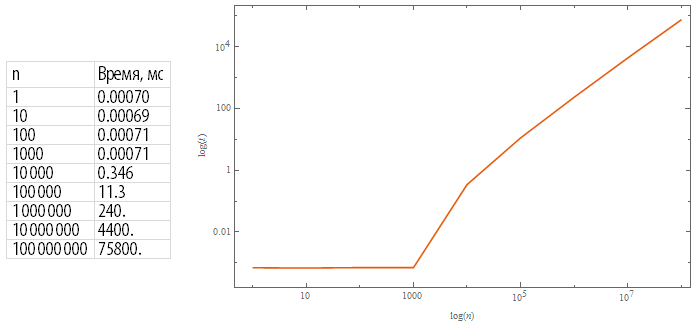
Код для копированияtimes=Table[{10^n,1000RepeatedTiming[(10^n)!;,5][[1]]},{n,0,8}]; Row@{Grid[{{n,"Время, мс"}}~Join~({#[[1]],NumberForm[#[[2]],5]}&/@times),ItemStyle->Directive[FontSize -> 20,FontFamily->"Myriad Pro Cond"],Alignment->{Left,Center},Frame->All,FrameStyle->LightGray]," ",ListLogLogPlot[times,Joined->True,PlotRange->All,FrameLabel->{Log[n],Log[t]},ImageSize->500,PlotTheme->"Scientific"]}
SemenovVV
19.04.2015 17:05+1Предложенный автором Алгоритм вычисления факторизацией можно немного улучшить, если учесть, что у всех простых чисел больших N/2 степень в разложении = 1.
Например сделать два цикла:
первый от 2 до N/2 — как есть,
второй от N/2 + 1 до N — оставить только решето Эратосфена




MichaelBorisov
Спасибо. Разумеется, эти ухищрения нужны только в случае, если нам нужно точное значение факториала. В остальных случаях для больших N подойдет формула Стирлинга.
Также во многих формулах, где встречаются факториалы, они встречаются в виде частного. Если имеем N!/M!, при близких M и N, частное может быть не очень большим по абсолютной величине и содержать мало множителей, даже если m и n по отдельности большие и требуют длинной арифметики для их вычисления.
5nw Автор
n!/m! можно вычислять деревом как P(n — m + 1, n) :)
Либо из показателей факторизации n вычесть показатели факторизации m