Для всех ответственных конструкций необходимо проводить расчеты по предельным состояниям. В этой статье я представлю процесс создания расчетной конечно-элементной модели конструкции крупногабаритной вакуумной камеры с последующим анализом прочности и устойчивости. Проведение расчетов на прочность и устойчивость – один из важнейших этапов итерационного процесса проектирования сложных конструкций.

Далеко не все расчетные комплексы позволяют смоделировать конструкцию сложной формы поверхностными конечными элементами, а тем более использовать в одной расчетной модели несколько типов конечных элементов. Для анализа конструкции крупногабаритной вакуумной камеры я буду использовать расчетный комплекс Femap с NX Nastran. В ходе работ определю напряженно-деформированное состояние (НДС) крупногабаритной вакуумной камеры (рис. 1) и критическую силу потери устойчивости, представлю вариант улучшенной конструкции, а также расскажу о нелинейном анализе потери устойчивости.


Рис. 1. Геометрическая модель крупногабаритной вакуумной камеры

Введение

Испытания на герметичность в вакуумной камере проводят с целью проверки способности летательных или подводных аппаратов, корпусов изделий либо отдельных блоков и частей не допускать проникновения воздуха или воды в корпус отсека или аппарата. При этом в процессе испытаний сами вакуумные камеры подвергаются значительным нагрузкам от разницы давления внутри и снаружи камеры.

Цикл пневмовакуумных испытаний крупногабаритной техники является наиболее объективным методом, позволяющим в наземных условиях контролировать соблюдение жестких требований к герметичности отсеков и бортовых систем. Значительные нагрузки, с которыми связаны испытания, требуют изготавливать крупногабаритные вакуумные камеры из стали большой толщины и с ребрами жесткости, а предварительно проводить расчеты камер на прочность и устойчивость.

Описание конструкции вакуумной камеры

Исследуемая вакуумная камера состоит из цилиндрической обечайки, собранной из сегментов, и двух полигональных крышек, усиленных ребрами жесткости. Одна из крышек жестко прикреплена к цилиндрической части, другая является откидной. Камера крепится к основанию с помощью шести опор.

Вакуумная камера выполнена из стали с модулем упругости 2∙10^11 Па, коэффициентом Пуассона 0,3, плотностью 7850 кг/м3, пределом текучести 270 МПа. Расчетная нагрузка составляет 10^5 Па. Согласно рекомендациям из книги А.С. Вольмира «Устойчивость упругих систем» примем коэффициент запаса по устойчивости равным 0,5 (то есть критическая сила потери устойчивости – не менее 2). Применение данного коэффициента обусловлено наличием начальных неправильностей формы и другими факторами.

Потеря устойчивости оболочек, как правило, происходит внезапно, с образованием глубоких вмятин, обращенных к центру кривизны.

Габариты вакуумной камеры 18,5 на 13,5 м.

Разработка модели. Создание геометрической модели вакуумной камеры

Исходные данные для вакуумной камеры были представлены в виде эскизов (по информации из свободных источников), после чего создана трехмерная модель камеры. Затем трехмерная модель в формате STEP импортирована в Femap с NX Nastran, встроенными инструментами которого были построены серединные поверхности.

Такая модель пригодна для дискретизации на конечные элементы (КЭ) типа «плоская оболочка» («plate»). Этот подход позволяет создать достаточно точную расчетную модель конструкции при меньшей, чем в случае использования трехмерных конечных элементов, размерности матрицы жесткости.

На рис. 2-4 представлена поверхностная геометрическая модель вакуумной камеры.


Рис. 2. Геометрическая модель вакуумной камеры


Рис. 3. Геометрическая модель вакуумной камеры. Крышка


Рис. 4. Геометрическая модель вакуумной камеры. Опоры

Для удобства задания и последующей корректировки толщин части модели бы объединены в группы (рис. 5).


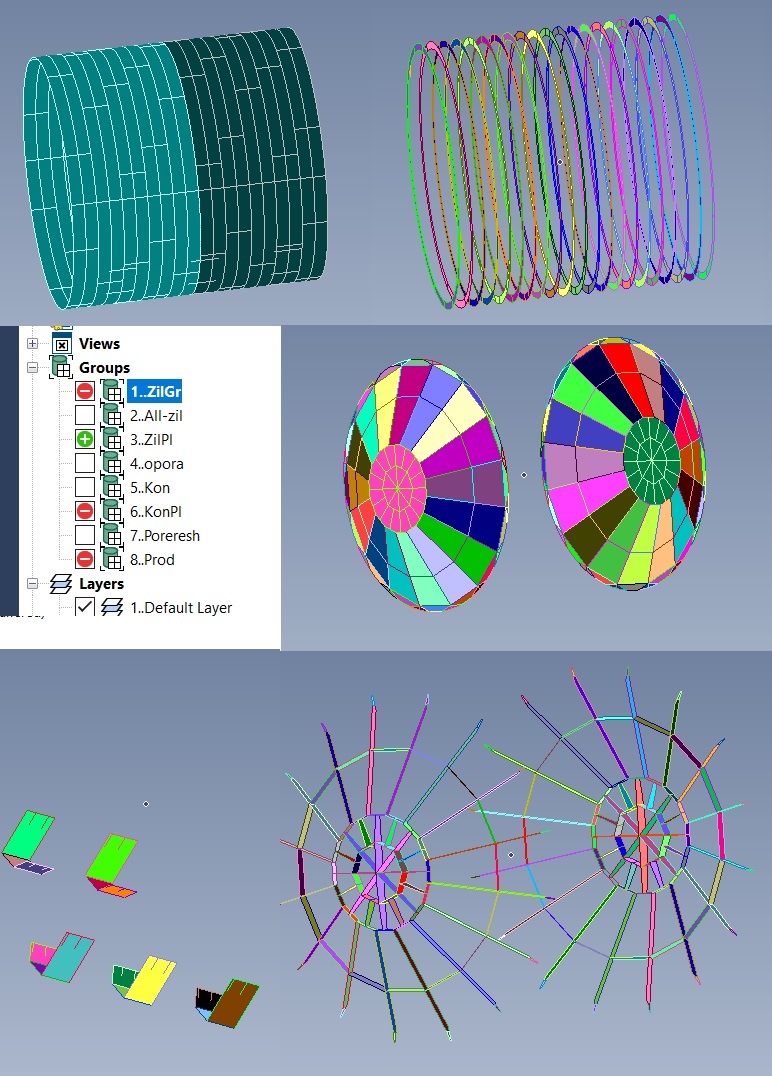
Рис. 5. Геометрическая модель вакуумной камеры. Группы

Создание конечно-элементной модели

На основе геометрической модели была создана КЭ-модель вакуумной камеры. Большая часть конструкции разбита четырехугольными пластинчатыми конечными элементами. Число треугольных пластинчатых элементов невелико, они использовались для построения сетки в переходных областях (рис. 6).


Рис. 6. Конечно-элементная геометрическая модель вакуумной камеры

В исходном первом варианте конструкции толщина цилиндрической части и пластин днища составляет 0,02 м, толщина ребер 0,025 м.

Расчет НДС и устойчивости вакуумной камеры

Результаты линейного статического анализа таковы, что после приложения нагрузки в 10^5 Па максимальные перемещения составляют 0,027 м от прогиба крышки, максимальные напряжения – 26 МПа в цилиндрической части, 87 МПа на крышке. То есть напряжения в целом значительно ниже предела текучести (рис. 7).


Рис. 7. НДС вакуумной камеры

Результаты анализа устойчивости вакуумной камеры показывают, что первые 24 формы потери устойчивости реализованы на крышках камеры. Это означает, что цилиндрическая часть камеры обладает большей жесткостью по сравнению с крышками. При этом критическая сила потери устойчивости составляет 1,34, что меньше допустимых 2 (рис. 8).


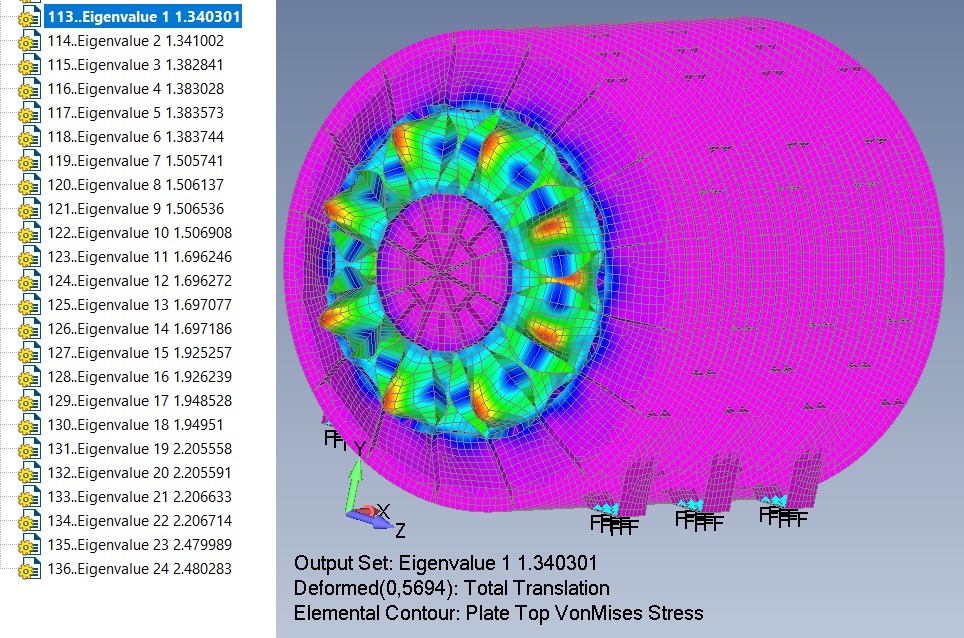
Рис. 8. Формы потери устойчивости вакуумной камеры

При переходе к анализу следующего варианта конструкции усилим крышку: увеличим толщину ее пластин, добавим на обе крышки третье кольцо ребер жесткости.

Второй вариант конструкции: толщина цилиндрической части 0,02 м, толщина пластин днища составляет 0,025 м, ребра 0,025 м; на обе крышки добавлено третье кольцо ребер жесткости (рис. 9).


Рис. 9. Конструкция вакуумной камеры с дополнительным кольцом ребер жесткости на крышках

Результаты линейного статического анализа таковы, что после приложения нагрузки в 10^5 Па максимальные перемещения составляют 0,018 м от прогиба крышки, максимальные напряжения – 25 МПа в цилиндрической части и 70 МПа на крышке (рис. 10-12).


Рис. 10. НДС вакуумной камеры


Рис. 11. Напряжения в элементах крышки


Рис. 12. НДС вакуумной камеры

На рис. 13 видно, что в месте стыковки крышки и цилиндрической части напряжения в локальных областях превышают предел текучести. В этих местах необходимо предусмотреть локальные усиления конструкции.

Появление дополнительных колец ребер жесткости на крышках значительно увеличило жесткость крышек – это хорошо видно при сравнении форм потери устойчивости.

Первые 32 формы потери устойчивости реализуются на ребрах жесткости крышки, 33-я (рис. 14) и следующие – на плоских сегментах между ребрами жесткости. Это означает, что цилиндрическая часть камеры обладает большей жесткостью. При этом критическая сила потери устойчивости для первой формы составляет 6,35.


Рис. 13. 1-я форма потери устойчивости крышки вакуумной камеры


Рис. 14. 33-я форма потери устойчивости крышки вакуумной камеры

Формы потери устойчивости из линейного анализа можно использовать при создании «дефектов» в нелинейном анализе. Как следует из названия, линейный анализ потери устойчивости не учитывает нелинейности. Соответственно все контакты и свойства материалов считаются линейными, не учитываются эффекты больших перемещений. Эти факторы делают полученную критическую нагрузку неконсервативной.

Нелинейный анализ как инструмент для оценки потери устойчивости

При проведении нелинейного анализа вакуумной камеры была учтена только нелинейность, связанная с большими перемещениями, потому результаты анализа для данного конкретного расчета являются адекватными только в диапазоне нагрузок до достижения предела текучести. Однако на примере этого расчета мы расскажем о теоретических и практических основах применения нелинейного анализа для оценки потери устойчивости.

По результатам линейного анализа критическая сила потери устойчивости для первой формы составляет 6,35. С целью исследования устойчивости вакуумной камеры зададим нагрузку, в 10 раз превышающую эксплуатационную нагрузку: 10^5 Па, количество шагов приращения нагрузки – 20.

При решении нелинейной задачи заданные нагрузки будут приложены к телу не сразу. В нелинейном анализе нагрузки прикладываются постепенно и фактически решатель последовательно решает множество задач. При линейном статическом анализе всегда делается лишь один шаг: от начального состояния к конечному.

После запуска нелинейного анализа в Femap отображается график (рис. 15), иллюстрирующий в реальном времени количество выполненных итераций и (в случае нашего нелинейного статического анализа) Load Factor, то есть фактор нагрузки от 0 до 1. В правом верхнем углу мы видим информацию о номере текущей итерации (именно так, а не номер шага приращения нагрузки). Каждый шаг приращения нагрузки может содержать в себе несколько итераций – это необходимо для выполнения алгоритмов, реализующих сходимость решения. Если приращение не сходится, это означает, что изменение в нагрузке слишком велико, чтобы перейти к следующему шагу; нагрузка снижается – выполняются дополнительные итерации внутри одного шага.

Вблизи точки геометрической нестабильности Nastran будет делить шаг пополам до достижения максимального количества итераций. При проведении нелинейного анализа вакуумной камеры сообщение с пояснением, что решение не сходится, появилось при уровне нагрузки 0,8 (128-я итерация) – потеря сходимости обусловлена геометрической нестабильностью. Геометрическая нестабильность является причиной потери устойчивости: наклон на графике «сила – перемещение» почти нулевой (чем больше номер решения, тем больше уровень нагрузки), что делает невозможным получение решения. Таким образом, потеря сходимости решения сигнализирует о потере устойчивости конструкции. Более подробно о нелинейном анализе и сходимости рассказано в моей статье «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна».


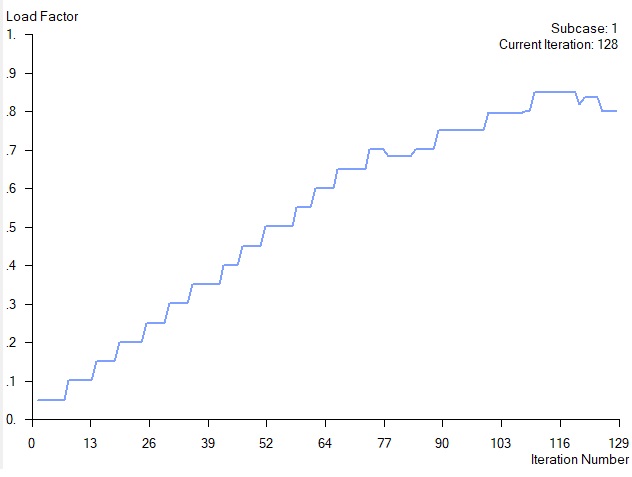
Рис. 15. График сходимости решения при нелинейном анализе вакуумной камеры

Напряжения на крышке достигают предела текучести при нагрузке 350 000 Па (в 3,5 раза больше рабочей). То есть пластические деформации в элементах конструкции вакуумной камеры начнутся задолго до потери устойчивости.

Важно отметить, что потеря устойчивости может происходить и в области пластических деформаций, потому в некоторых случаях нелинейный анализ является незаменимым инструментом.

Заключение

В процессе анализа вакуумной камеры методом конечных элементов рассмотрены два варианта конструкции. При переходе от первого ко второму варианту была усилена крышка. Второй вариант конструкции в целом удовлетворяет условиям прочности и устойчивости. В местах концентрации напряжений необходимо выполнить местное усиление.

Femap с NX Nastran обладает инструментами, позволяющими производить нелинейный анализ потери устойчивости конструкций с учетом всех видов нелинейностей.

Эта работа выполнена мною в соавторстве (акт приема-передачи документации, авторского права, интеллектуальной собственности, информации от 27 июня 2021 года) с Денисом Александровичем Мироновым, предоставившим описание и эскизы типовой крупногабаритной вакуумной камеры, подготовленные им с помощью материалов из открытых источников информации.

Уважаемые читатели, приглашаю вас на онлайн-конференцию по инженерному анализу Simcenter Femap Симпозиум 2021 (15, 16 сентября в 11:00). Специалисты российских промышленных компаний и разработчики Femap из компании Siemens поделятся инженерным опытом и навыками в сфере конечно-элементного моделирования. Чтобы подробнее узнать о симпозиуме, пройдите по ссылке.



Бесплатную пробную версию Femap с NX Nastran можно скачать здесь.

Литература
1. Вольмир А.С. Устойчивость деформируемых систем. М.: Наука, 1967
2. Basic Nonlinear Analysis User’s Guide. Siemens.

Филипп Титаренко, специалист по расчётам на прочность,
продакт-менеджер по направлению Femap АО «Нанософт»
E-mail: titarenko@nanosoft.pro