Всем привет, меня зовут Максим Шаланкин, в Ситимобил я занимаюсь машинным обучением. Мы используем множество крутых алгоритмов для оптимизации наших сервисов и улучшения бизнес-процессов. В этой публикации я расскажу, как использовать в геоаналитике алгоритм ядерной оценки плотности (Kernel Density Estimation) и строить полигоны на карте, основываясь на распределении географических данных.

Про данные, проблему и алгоритм

Когда возникает задача создания полигона?

Все, кто работают с географическими данными, сталкиваются с такими структурами, как точка, линия и область, имеющими координаты. Когда у вас много точек на карте (дома клиентов, магазины, курьеры), возникает желание объединить точки в несколько групп. Можно воспользоваться любым алгоритмом кластеризации, но иногда это излишне. Мы можем применить алгоритм KDE, когда у нас уже есть признак, по которому точки на карте условно линейно разделимы (с некоторой погрешностью). По этому признаку мы будем строить полигоны, в которые войдут топ n% рассматриваемых данных.

Прикладная проблема, которую мы будем решать

Мы в Ситимобил используем KDE в задачах определения гео районов, для отрисовки статистики на картах, для реализации бизнес логик. Но для того, чтобы вы сами могли воспроизвести этот алгоритм на реальных данных, давайте решим задачу определения центра Санкт-Петербурга, а также построим карту этажности домов.

Открытые данные для решения задач

В открытом доступе на сайте реформы ЖКХ можно найти информацию о жилых домах для многих городов России. Для Санкт-Петербурга данные разделены на Ленинградскую область и сам город. Скачиваем файл в формате .csv и смотрим, что мы можем использовать для решения нашей задачи.

• address — адрес в формате строки;

• floor_count_max — наибольшее количество этажей;

• exploitation_start_year — год ввода в эксплуатацию.

Помимо этого в файле есть еще 60 столбцов самых разных признаков, от энергоэффективности дома до общей площади парковочной зоны.

Для дальнейшей работы нам нужно получить из строкового представления адреса его координаты. Сделать это можно через любой доступный геокодер. Для начала посмотрим, на что способен алгоритм KDE, какие у него есть параметры и как они влияют на отрисовку полигонов. Делать это будем на примере задачи нахождения центра Санкт-Петербурга.

Как работает алгоритм

По сути алгоритм работает как 2D-гистограмма, на основе которой мы можем получать линии уровня — желаемые полигоны. Форма финальных линий напрямую зависит от нескольких параметров:

• метрика расстояния (euclidean, haversine и другие);

• тип усредняющего ядра (gaussian, epanechnikov, exponential, inear, cosine);

• размер окна для выбранного ядра.

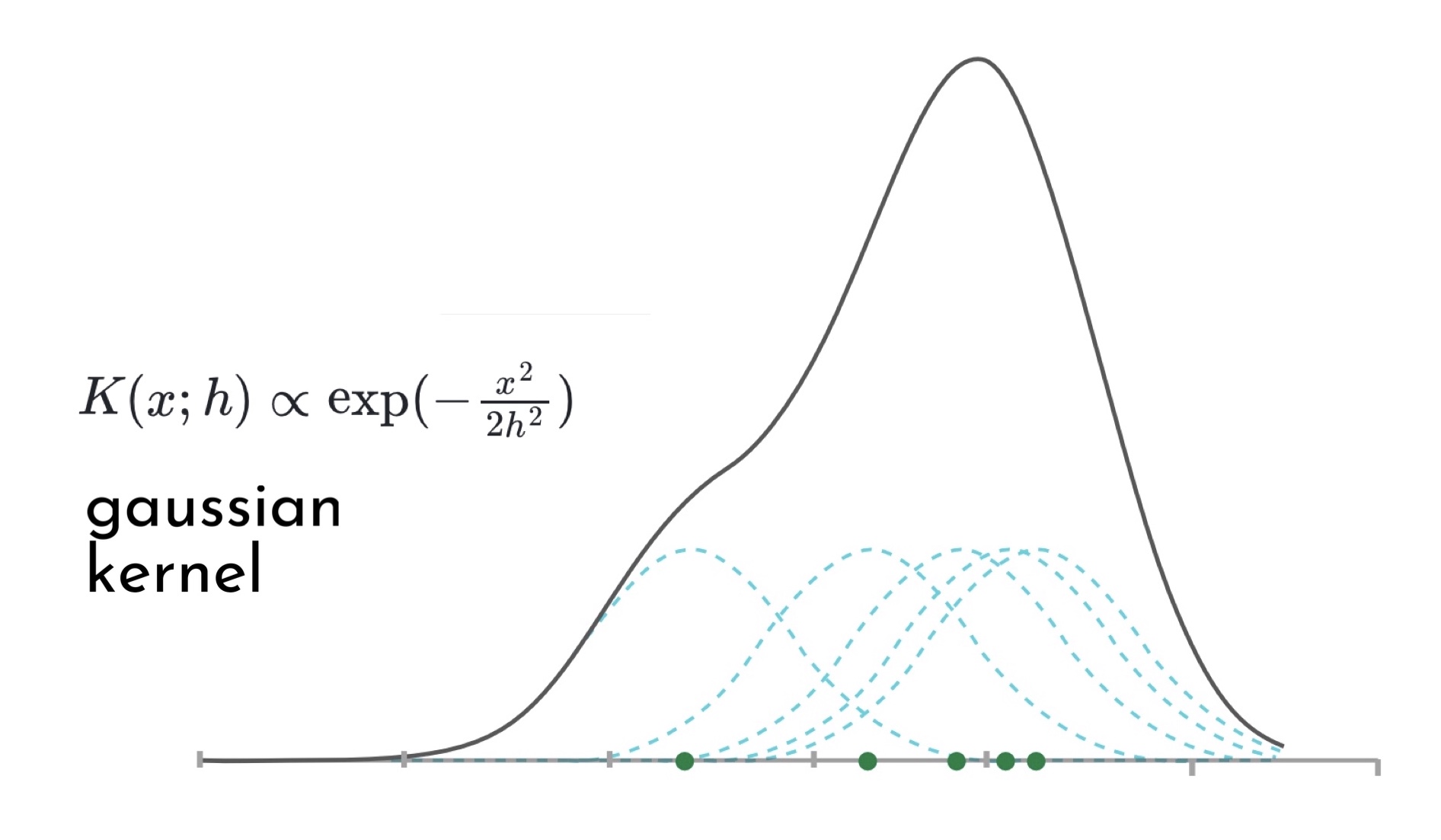
Для каждой точки данных нам нужно посчитать значение по формуле выбранного нами ядра, а затем просуммировать все ядра. Значение в каждой точке может меняться в зависимости от параметра h (или ширины окна ядра).

Сравним между собой работу двух метрик расстояния: euclidean и haversine. А в рамках каждой метрики посмотрим, какие полигоны будут на выходе для каждого из описанных выше ядер.

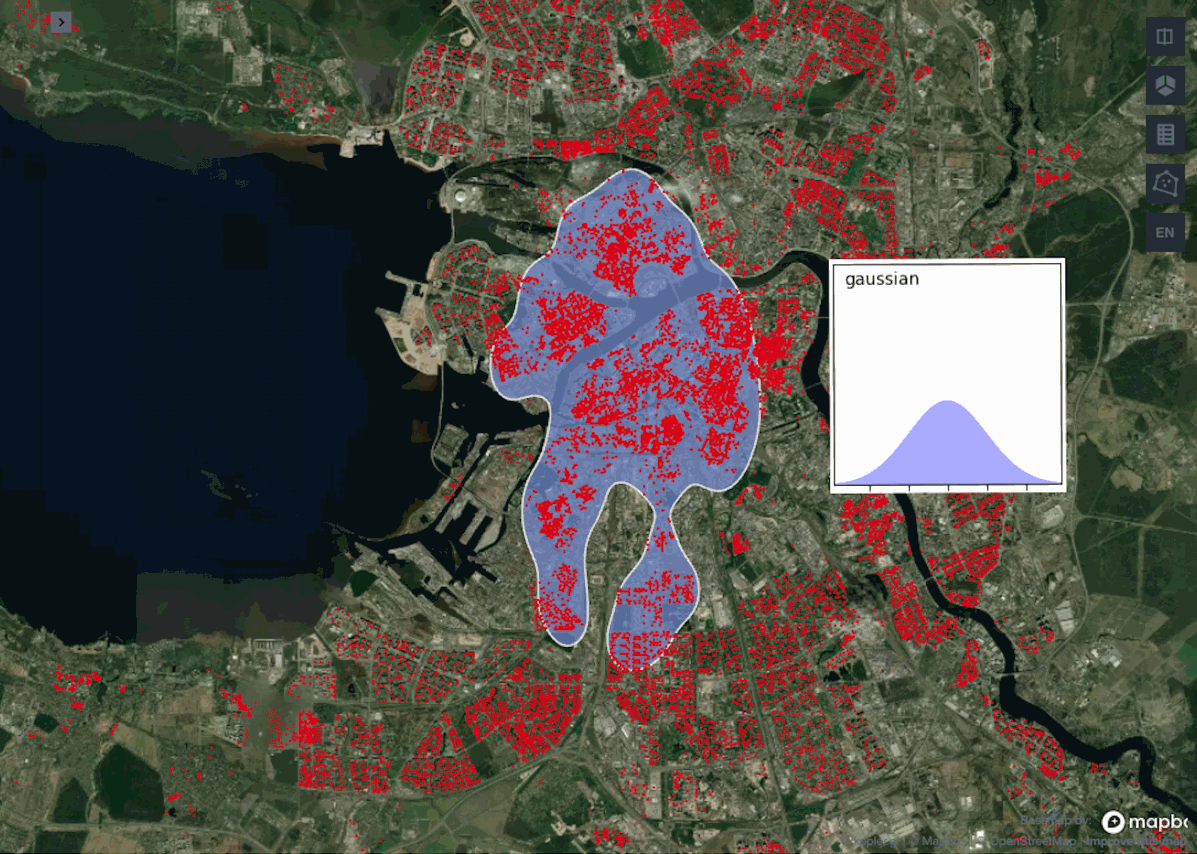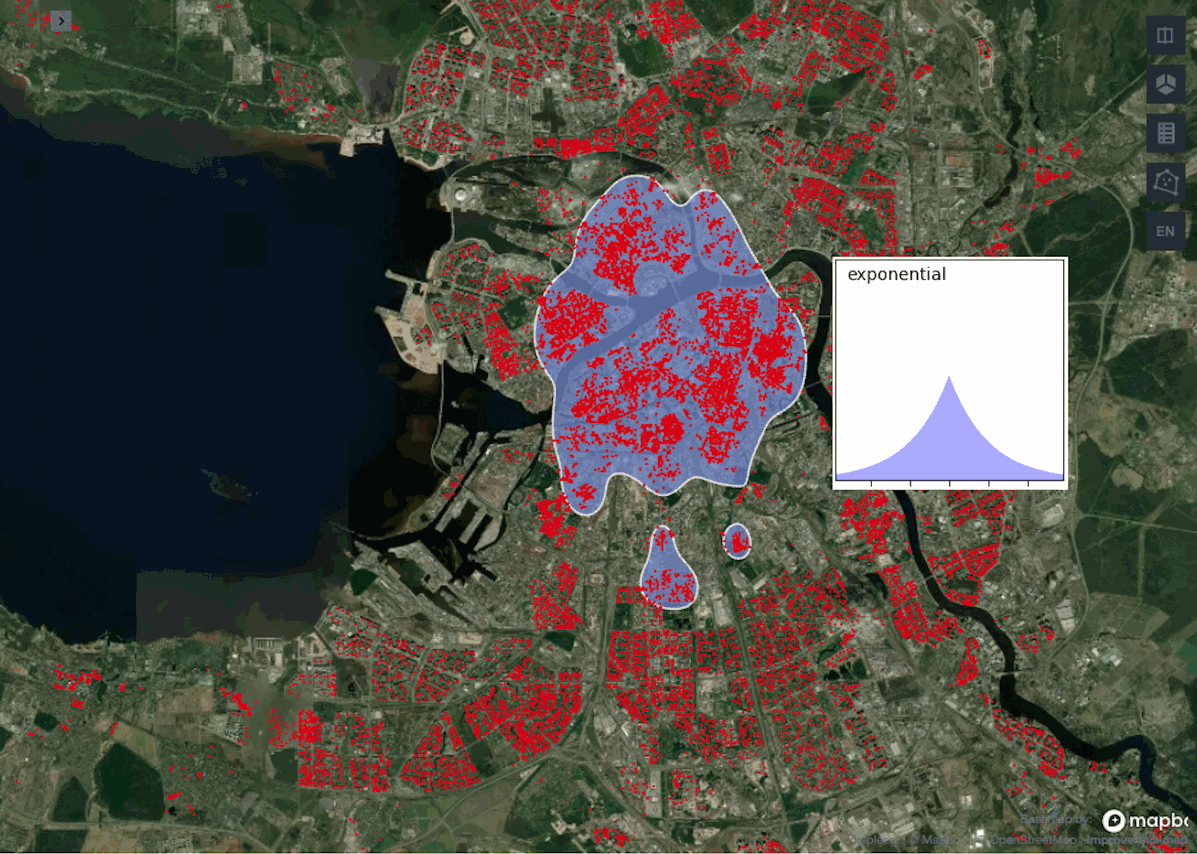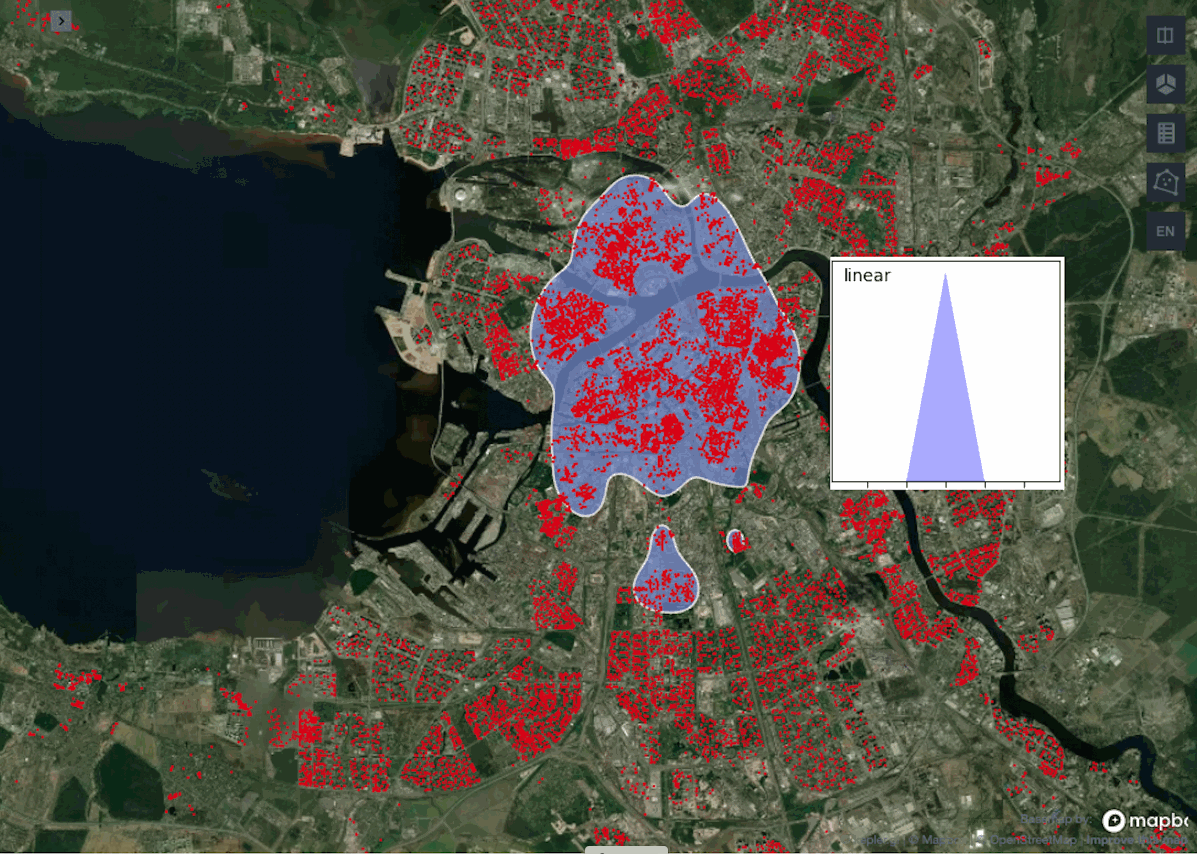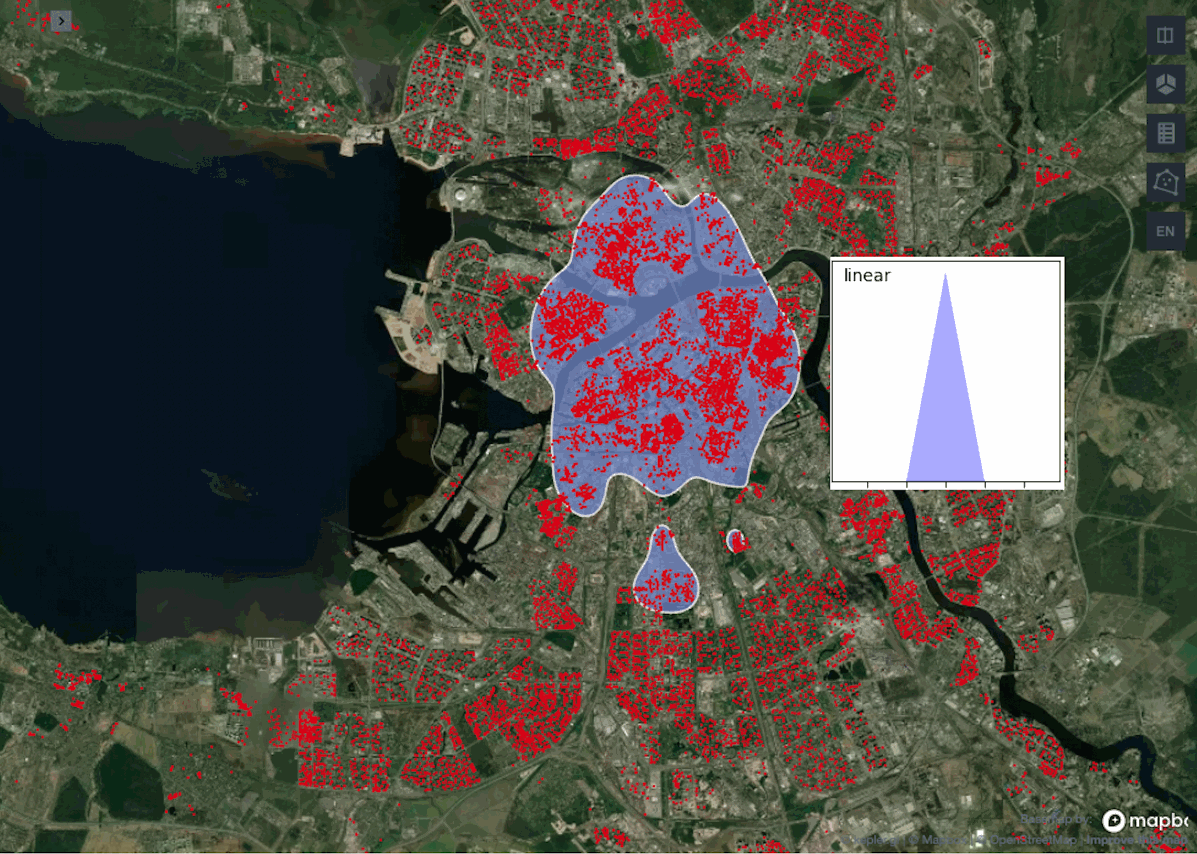
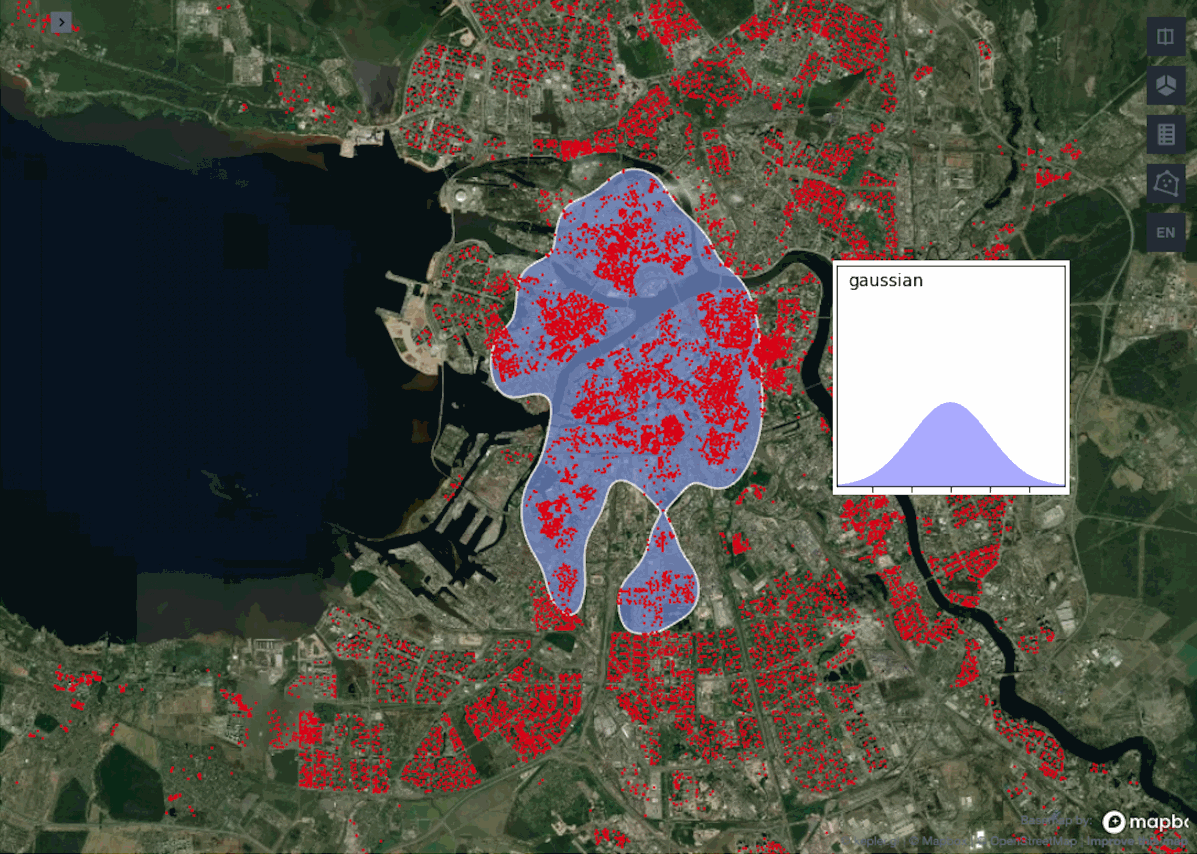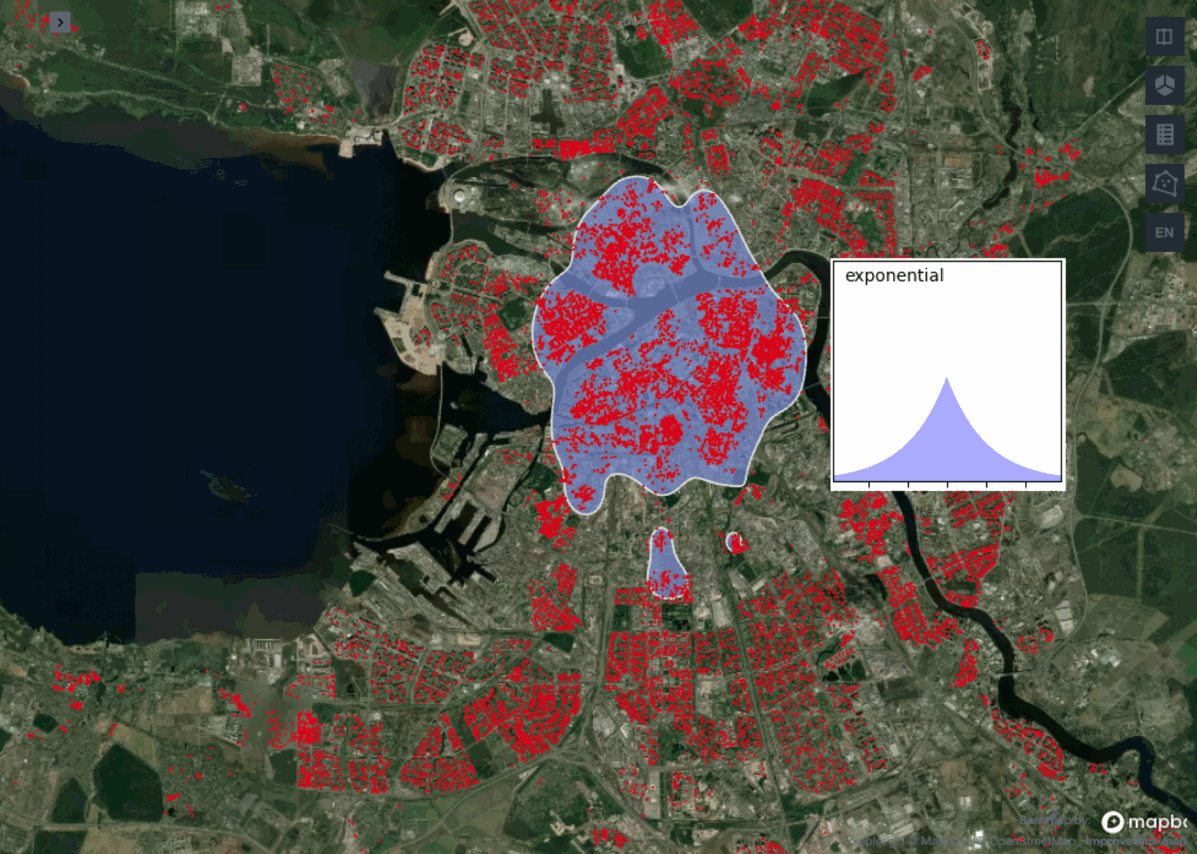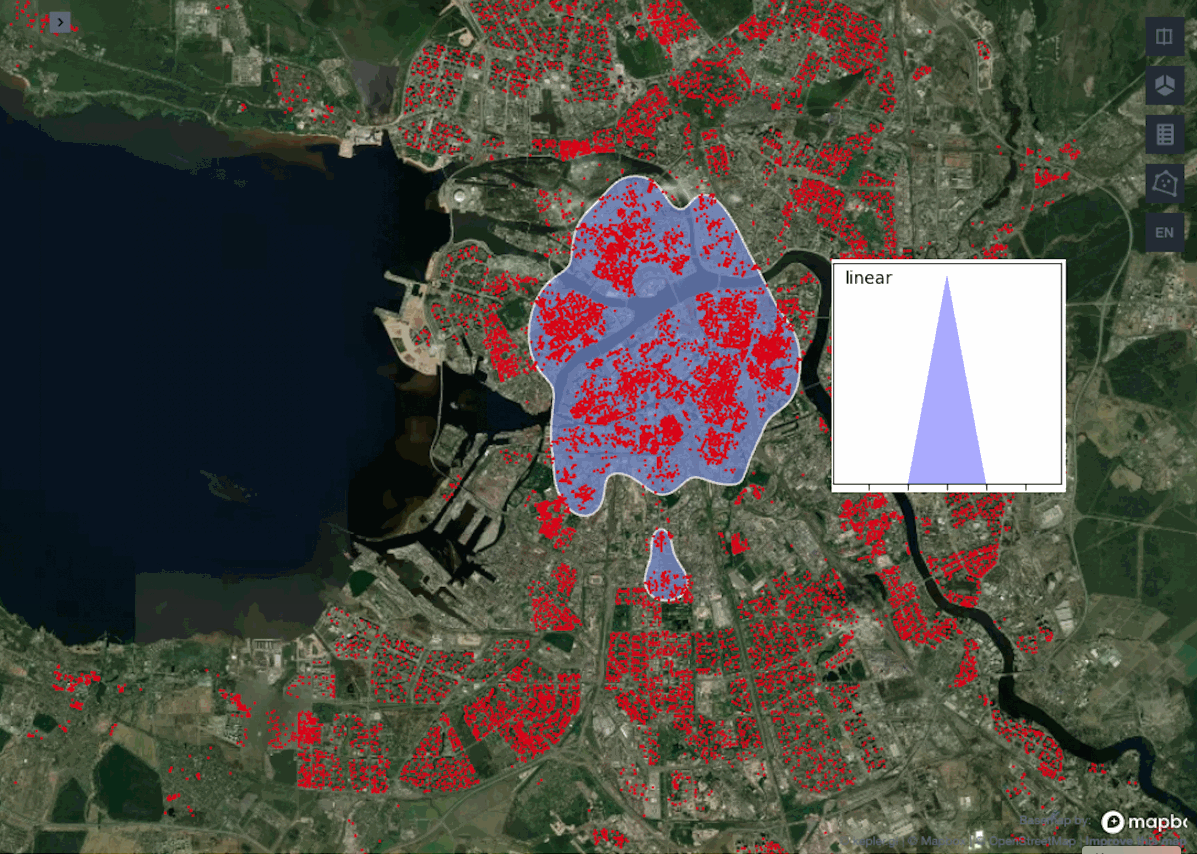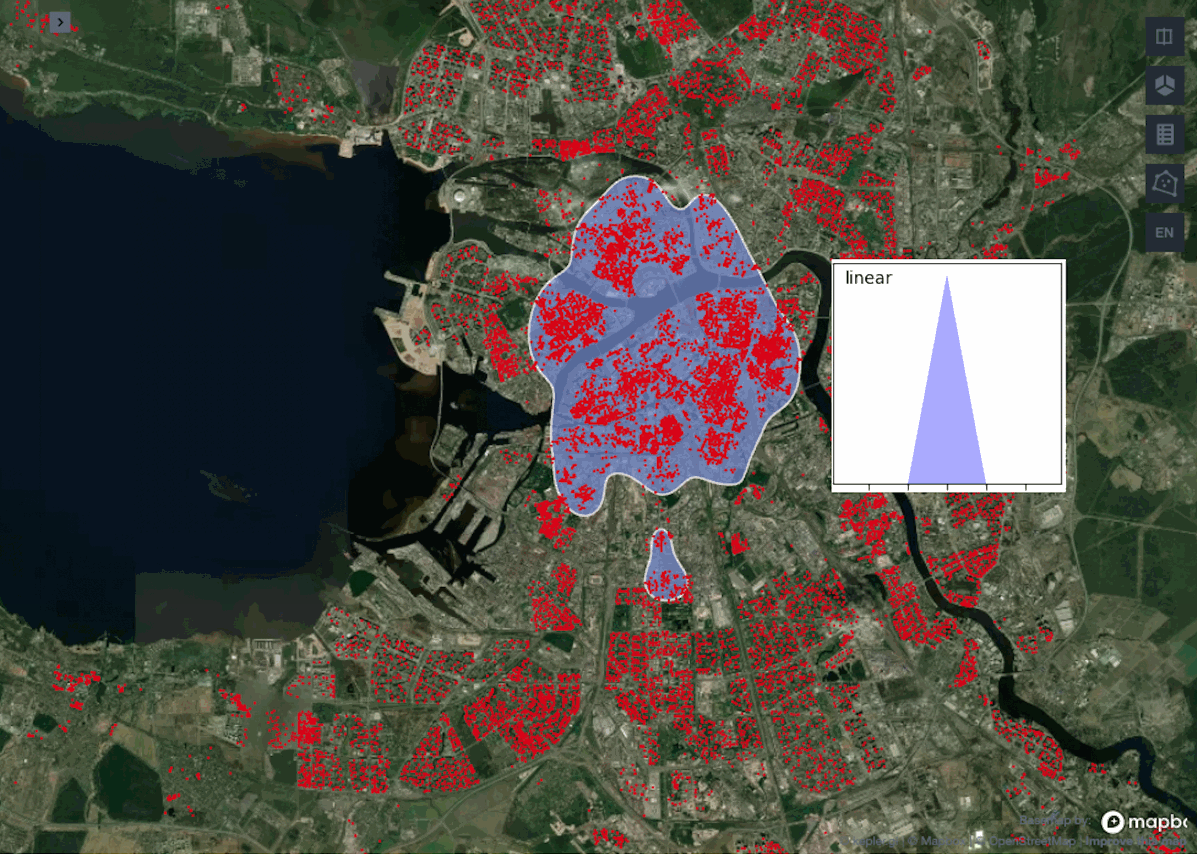
Наглядно видно, что между нашими функциями расстояния почти нет разницы. Это ожидаемо, потому что разница проявится только с увеличением масштабов географии, так как haversine учитывает кривизну Земли, а на небольших расстояниях ею можно пренебречь. К тому же с метрикой euclidean алгоритм работает ощутимо быстрее.

Сравнивая работу ядер можно заметить, что схожие результаты выдают gaussian, epanechnikov и cosine против exponential и linear. Обычно используют ядро gaussian, так как считается, что оно выдает самые точные результаты, но в нашем примере лучше взять exponential или linear, поскольку они не вытягивают наш центр города с севера на юг, а сохраняют полигон более округлой формы.

Посмотрим расширенную версию различных линий уровня для gaussian- и exponential- ядер.

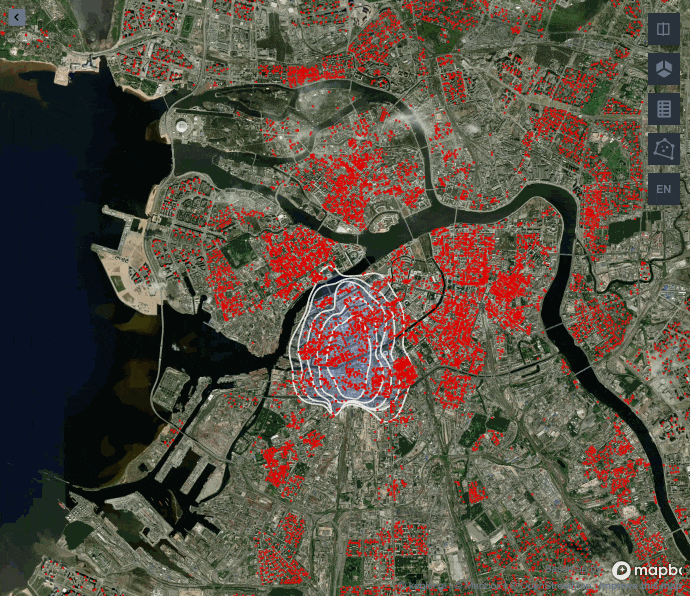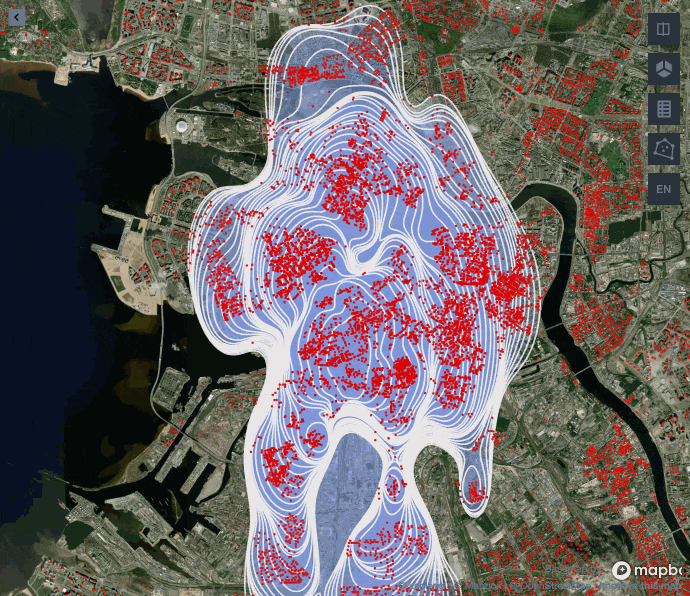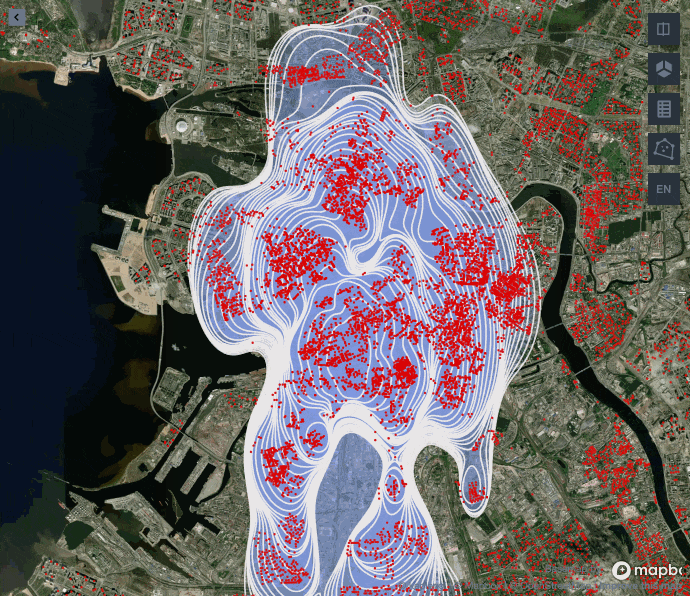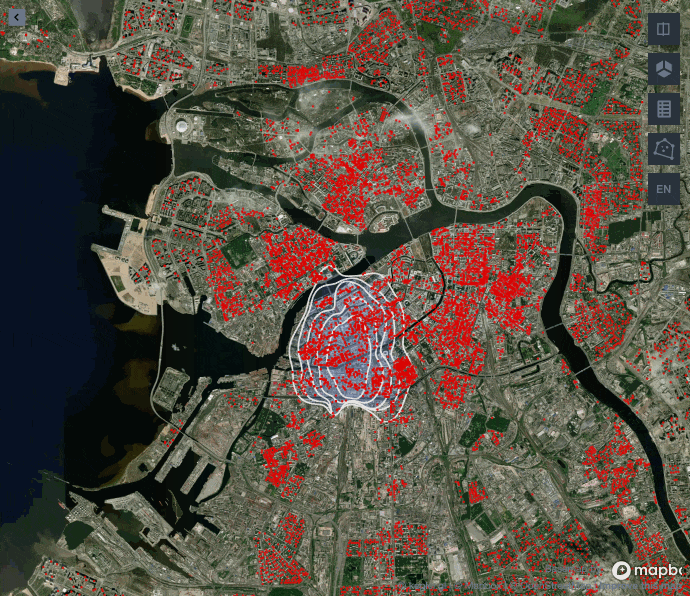
Как видите, до определенной доли обводимых точек полигон с экспоненциальным ядром лучше улавливает центрированную застройку Санкт-Петербурга, а гауссово ядро начинает сильно вытягиваться, игнорируя застройку на западе и востоке. Поэтому для нашей задачи лучше подойдет экспоненциальное ядро.

Остался последний не решенный вопрос: какой размер окна взять для выбранного нами ядра? Обычно от этого зависит то, какая граница будет у нашего полигона: гладкая и ровная или резкая и прерывистая. Попробуем изменить параметр bandwidth и посмотрим, как изменится финальная картинка центра города на уровне 25 %.

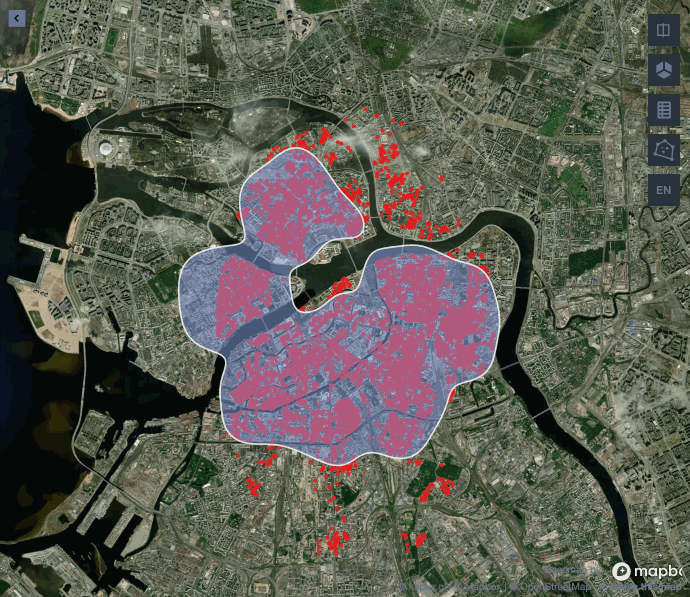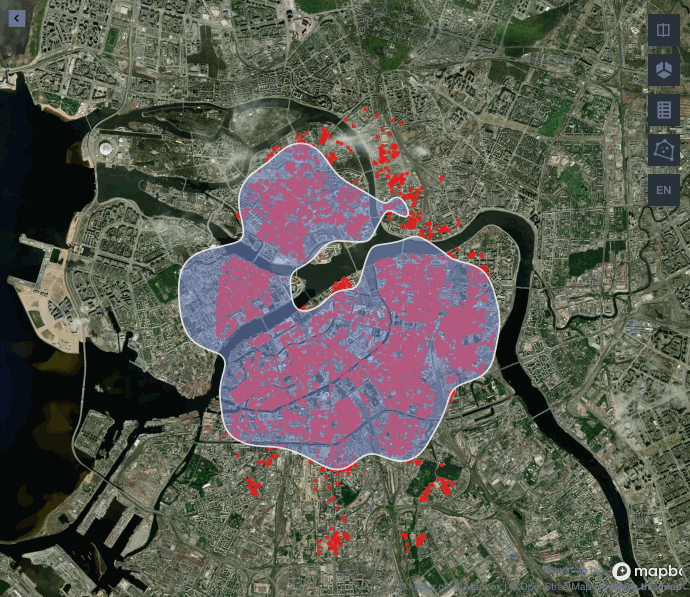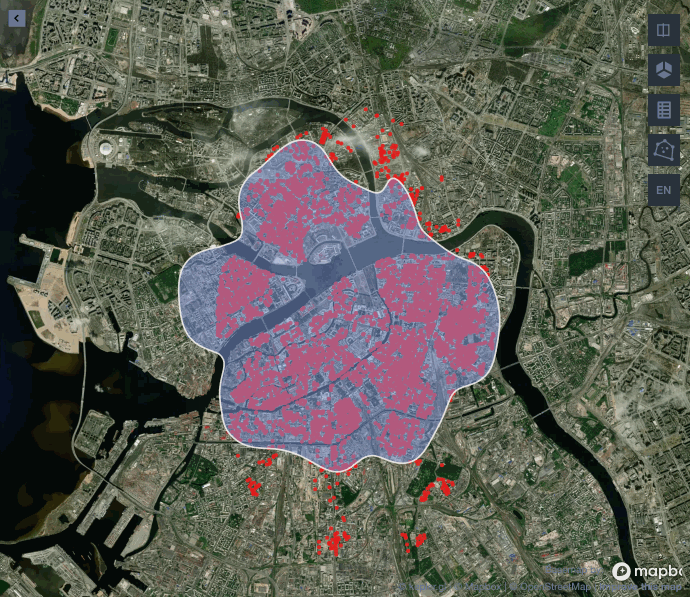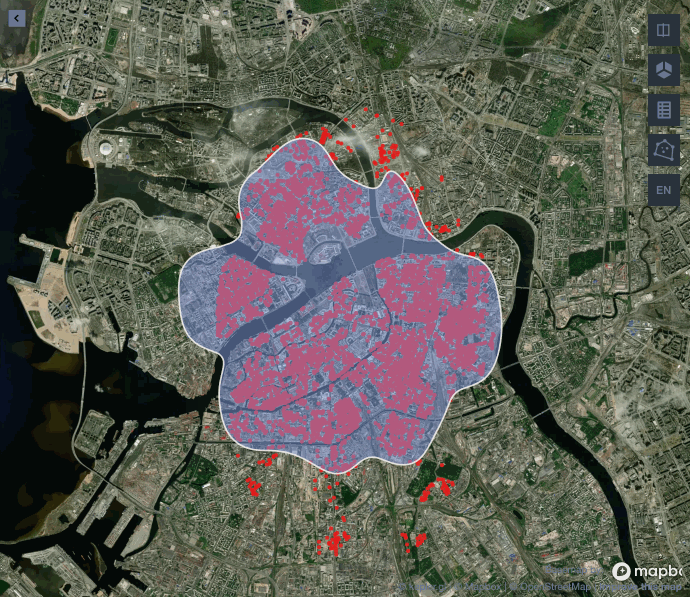
При значении близком к 0,01 алгоритм не включает в полигон часть реки, где нет домов, а с увеличением окна река становится частью полигона. Можно достаточно гибко подойти к выбору значения bandwidth, но для нашей задачи наличие части реки в полигоне не проблема. Поэтому остановимся на стандартном значении 1 для получения более гладкой границы.

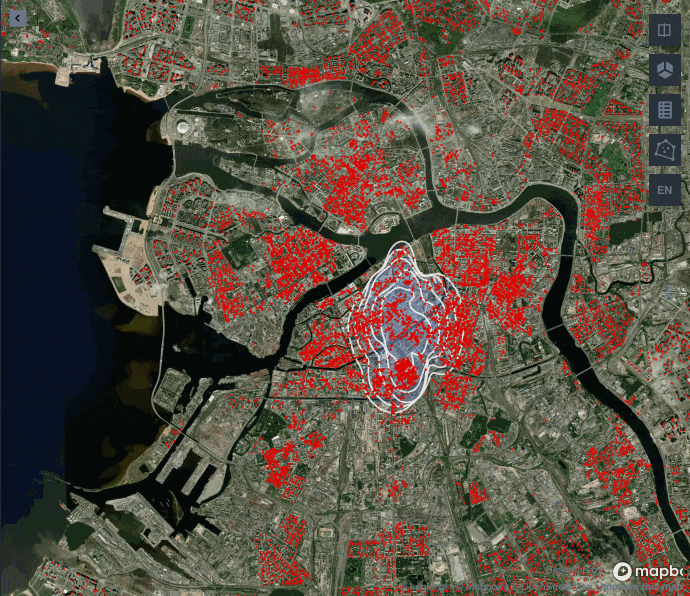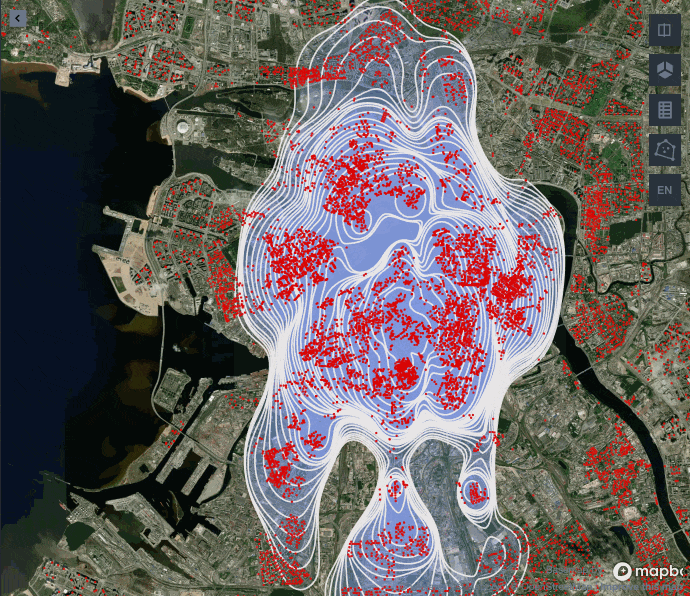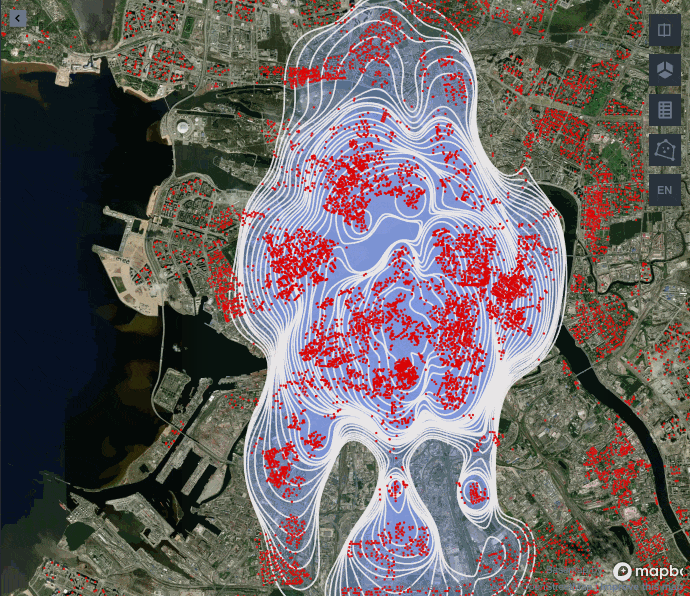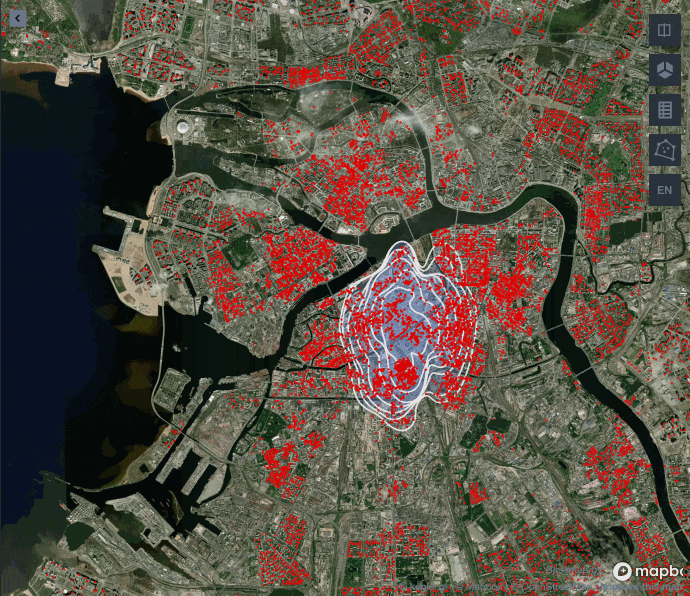
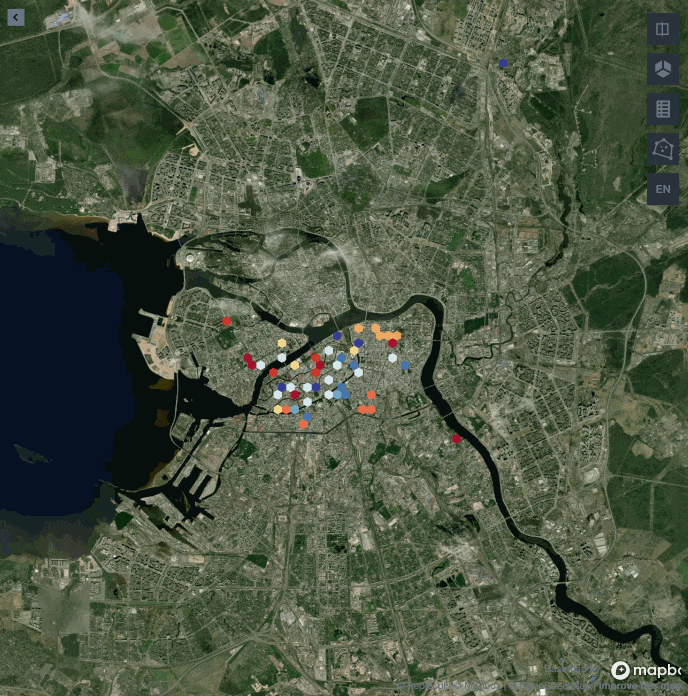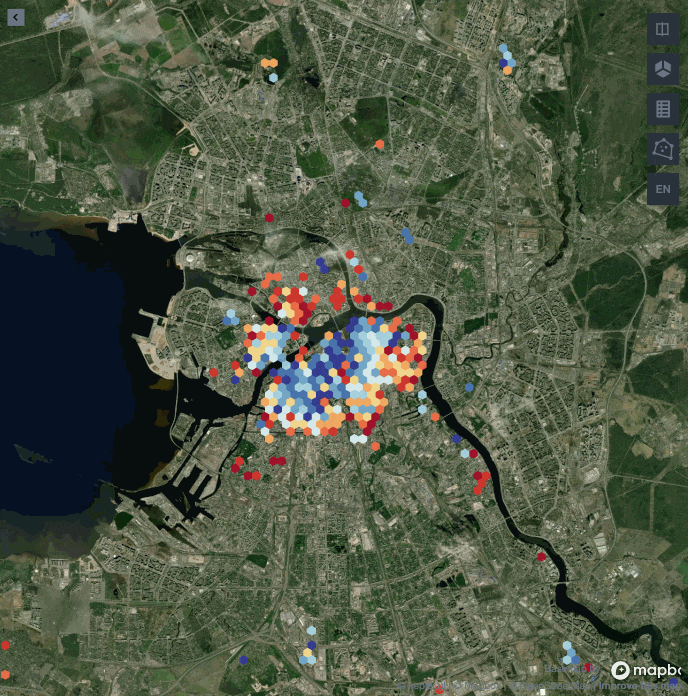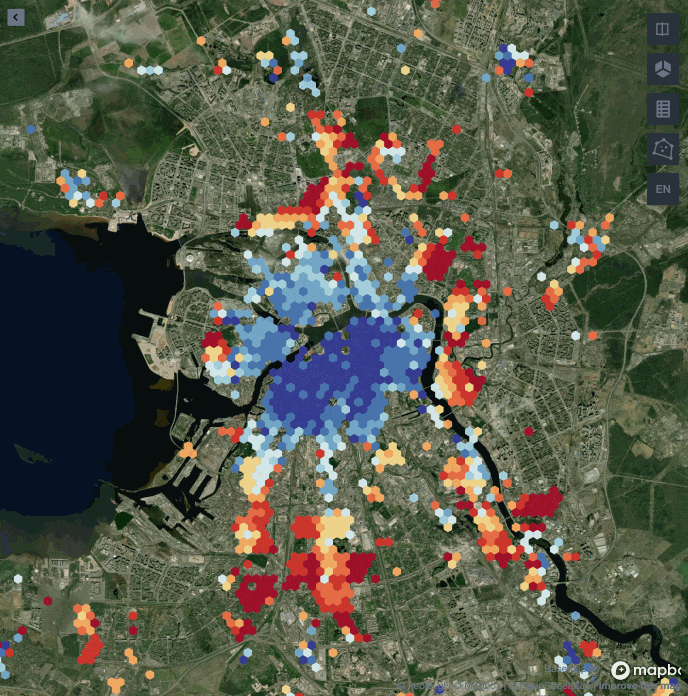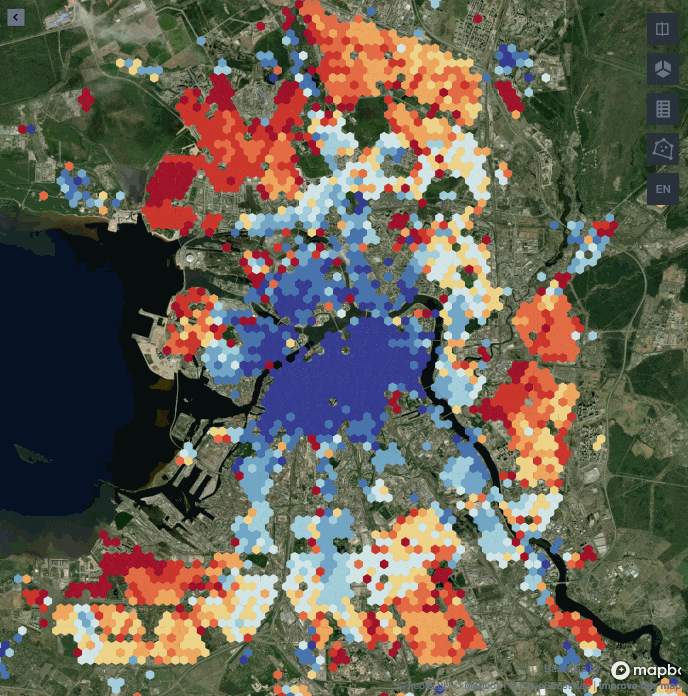
Как же выглядит центр Питера согласно алгоритму?

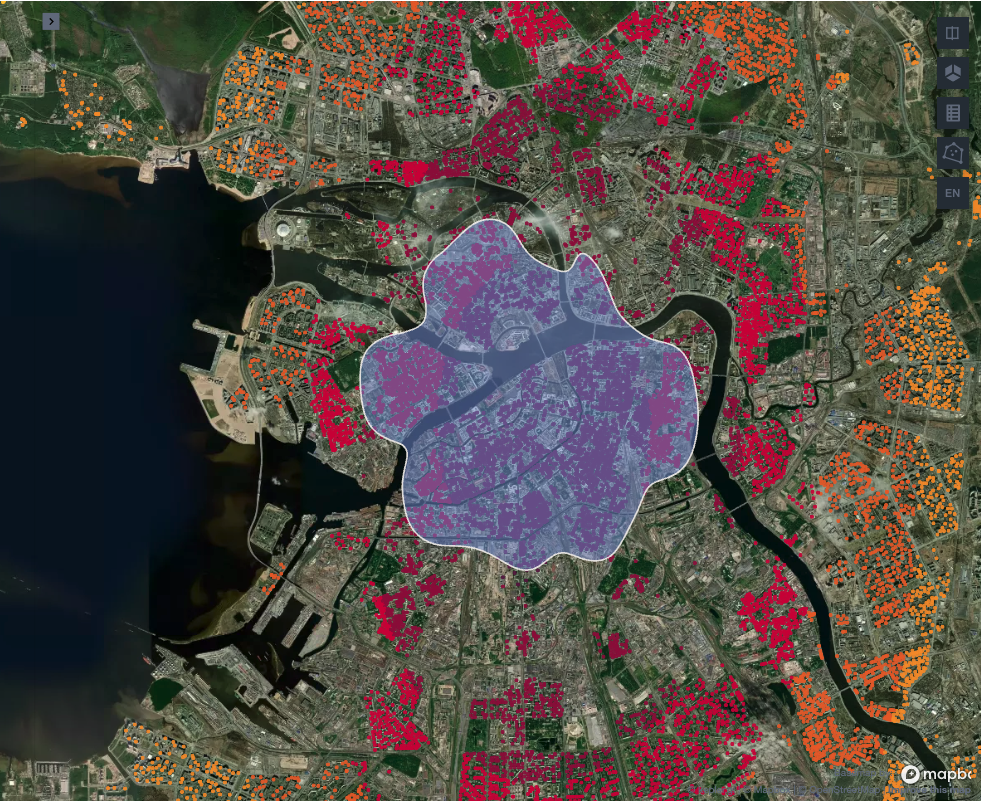
Здесь отрисован полигон в 25 %, а цветом обозначены значения для каждого дома, которые мы получили благодаря алгоритму KDE. Если вы потом заглянете в бонусную панель, то увидите, что центр мы определили достаточно точно, так как первые дома в Санкт-Петербурге появились именно внутри нашего полигона.

Карта этажности Санкт-Петербурга

Используя те же принципы, по которым мы нашли центр города, попробуем построить карту этажности, обводя полигонами распределение домов с одинаковым значением этажей. Чем ближе к красному, тем выше средняя этажность.

Мы видим три крупные зоны высокой этажности на севере, юге и востоке. Причем на севере сконцентрированы самые высокие дома. Центр Санкт-Петербурга канонично застроен пятиэтажными домами.

Как это использовать

Зная полигоны для каждой конкретной группы точек, мы можем:

• проверять вхождение новой точки в одну из групп;

• смотреть на пересечения построенных нами полигонов и искать в этих местах инсайты;

• создавать геозоны для реализации определенной бизнес-логики;

• сравнивать площади одних и тех же полигонов во времени и следить за их изменением.

Бонусная панель

Ниже представлена визуализация застройки Санкт-Петербурга с 1800 по 2020 год. В каждый момент времени на карте одним цветом обозначена группа домов, построенных в одно время.

Чем ближе к красному, тем позже был построен дом.

В работе использовались следующие python библиотеки:

• sklearn - для получения числовых значений KDE для каждого дома

• shapely - для работы с объектами полигонов

• keplergl - для отрисовки объектов на карте