
Дано: Есть игрушечная кольцевая железная дорога, состоящая из 13 одинаковых элементов.
Вопрос: какое минимальное количество таких элементов надо докупить, чтобы построить более длинную замкнутую, без пересечений, дорогу?
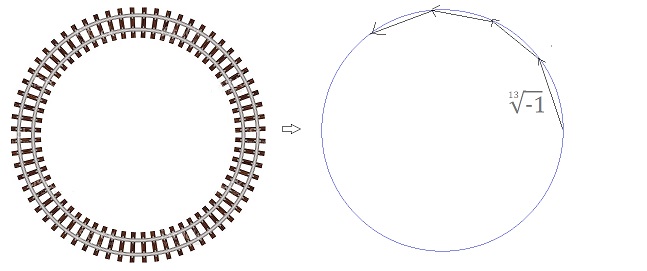
Корень 13 степени.
Решение и ответ под катом.
w = e^( 2π·i / 13)
Замкнутый контур выглядит так:
a0+a1w+a2w2+a3w3+a4w4+ a5w5+a6w6+a7w7+a8w8+a9w9+a10w10+a11w11+a12w12=0
Нам надо решить данное уравнение на уровне коэффициентов.
Здесь пахнет основной теоремой Гаусса:
Многочлен 1+x+x2+x3+x4+ x5+x6+x7+x8+x9+x10+x11+x12=0 — неприводим.
Следовательно, все «а» должны быть одинаковы.
Напрашивается ответ а=2, но если мы посчитаем суммарный угол, на который повернулся наш вектор, то он должен быть нечетным, поэтому а=3. Надо еще докупить 26 деталек.
Как же тогда будет выглядеть железная дорога?

Получится «волнистая окружность».

А какая ваша любимая задача по математике?
Оригинал:

Комментарии (72)

nerudo
08.10.2021 15:52+1А меня всегда занимало сделать генератор возможных конфигураций икейских ж/д (см. выше) из предопределенного количества деталей. Естественно, с учетом возможного некоторого люфта. Уже и дети подросли. Может с внуками потренируюсь.

nochkin
08.10.2021 16:58Кстати, по поводу внуков. Этот набор из IKEA на самом деле полностью совместим с его оригинальной (?) идеей от BRIO. Там есть много других интересных вариантов и наборов, которые можно добавить.
И, конечно, IKEA -- не единственные, кто делает совместимые наборы. Даже на Aliexpress есть свои варианты.

furtaev
08.10.2021 16:46+6Школьная задача...решение надо искать на комплексной плоскости.
А что, такие школы ещё где-то остались?

MagisterLudi Автор
08.10.2021 16:48+1Парочка есть
+ЗФТШ
+ ютюб
GospodinKolhoznik
08.10.2021 18:29+3ЗФТШ насколь я помню всегда оставалась в рамках школьной программы. Задачи там были повышенной сложности, но без заходов в ТФКП и общую алгебру.
Допустим в школе могут вскользь упомянуть формулу Эйлера. Но откуда школьник даже из крепкого физмат класса может знать критерии неприводимости многочленов и вообще что это такое? Савватеев преувеличивает по поводу того, что задача школьная.

MagisterLudi Автор
08.10.2021 18:32+1у меня во Вдадивостоке были в школе задачи из ТФКП
а в ЗФТШ каждая вторая в 10-11 классе
MagisterLudi Автор
08.10.2021 19:13+1и на выпускном экзамене в 11 классе была задача про геометрическое место точек на комплексной плоскости, ее правда даже учительница по математике на осилила, а мы с друганами сели втроем за одну парту и затащили, потом всем дали списать

DaneSoul
08.10.2021 18:03+1Если понимать под школьной задачей задачу для олимпиад школьников, то там на Всероссийском туре задачи такого уровня могут быть, что и университетских знаний не всегда хватает, по крайней мере по естественным наукам.

dmlogv
08.10.2021 16:56+4Делать (со стороны производителя) кольцо из 13 секторов — это какая-то содомия.
Зато есть реальный пример: железка из Lego Duplo, у которой кольцо собираются из (вчера посчитал) 12 элементов.

janatem
08.10.2021 17:03+2В подсказке ошибка на рисунке: должен быть корень тринадцатой степени из единицы (оно же $e^{2\pi/13}$), а не из минус единицы.

MagisterLudi Автор
08.10.2021 17:12точно, это я ошибся на 90 градусов
(с точностью до поворота) — задача обладает радиальной осевой симмертией\инвариантностью в нашем случае
WQS100
08.10.2021 19:14+1Тогда и в ответе лучше написать 2*pi*i/13, или пояснить, что такое "p", если такое обозначение было введено специально

tangro
08.10.2021 17:25+3Измените условие на "сколько минимально еще таких элементов надо докупить".
А то вот решение для 39 доп.элементов я придумал просто в уме, без всяких комплексных плоскостей.

GennPen
08.10.2021 17:56+8Решил не математическим, а логическим способом.
Раз у нас нечетное кол-во, то просто разъединить две половинки дороги и удлинить не получится. Тогда нужно удлинять сектора. Если взять два одинаковых сектора и соединить их наоборот (волнистой линией), то начало и конец будут параллельны. Подсоединяем эту часть к еще одному сектору и получается более длинная часть дороги с тем же углом. Соединяем эти длинные части воедино и получаем 3*13=39 частей (26 докупить). Можно еще удлинить и получим 5*13=65 (52 докупить), и т.д.

Celahir
08.10.2021 18:13+3Когда у вас есть кольцо из 39 частей, далее достаточно добавлять по 6 сегментов, по 2 сегмента в каждую из трех равных частей. Да, дорога будет меньше походить на кольцо, но будет собираться.

MagisterLudi Автор
08.10.2021 19:18да, это самый логичный ход решения, вот только в нем нет строгого доказательства невозможности построить более минимальный вариант, а через комплексную плоскость и формализацию — есть

Celahir
08.10.2021 17:57+4Для решения текущей задачи достаточно логики и базовой геометрии. Решать через комплексные числа интересно, но это уже универсальное решение для задачи с n-числом сегментов.
Тут достаточно сообразить, что кол-во дополнительных сегментов всегда чётно, т.к. сумма углов должна остаться неизменной. Минимальное количество изменяемых сегментов также является наименьшим делителем, так как дорога кольцевая. Вот только 13 - это простое число, соответственно изменять нужно все 13 сегментов. Поправьте, если я не прав.

DaneSoul
08.10.2021 18:06+2w= e^(2p/13)
Тут для не математиков явно требуется пояснение, что это такое и откуда взялось.
Tyusha
08.10.2021 19:36Тут у автора ошибка, должно быть w = e^( 2π·i / 13).
Каждый сегмент дороги представляется в виде вектора единичной длины (комплексного числа с модулем 1), повёрнутого на угол 360°/13. Последующие сегменты — это произведение комплексных w всех предыдущих сегментов, т.к. текущий прицеплен к их концу.
А вся цепочка дороги — есть сумма всех сегментов. Её замыкание означает равенство данной суммы нулю. Коэффициенты 'a' зависят от того, в какую сторону мы завернули каждый последующий сегмент, вправо или влево — "в плюс" или в "минус",

Anna-13
08.10.2021 18:33а нам с сыном вот этот способ помог в решении логических задач https://nauka.club/informatika/krugi-eylera.html

wataru
08.10.2021 18:36+2А можно помедленнее и поподробнее, пожалуйста? Теорема Гаусса — это про основную теоремму алгебры? Как из нее получается неприводимость многочлена 1+...+x^12? И особенно, как из этой неприводимости получается, что все a должны быть равны?
Далее тоже ничего непонятно.если мы посчитаем суммарный угол, на который повернулся наш вектор, то он должен быть нечетным
Что за суммарней угол тут считается? Если это про поворот вектора вдоль контура, то он, при всех a_i равных будет a, будет 2*pi*a. Чем тут a=2 не подходит — я тоже непонимаю.

MagisterLudi Автор
08.10.2021 19:20+1
MagisterLudi Автор
08.10.2021 19:22Обычно в учебниках пишут так:
«Очевидно, что многочлен ХХХ неприводим, поэтому...»

wataru
08.10.2021 19:56+2Спасибо. Остаются еще два вопроса — почему из-за неприводимости следует, что все a равны (Нет многочлена с корнем равным w, не делящегося на 1+...+x^12)? И почему a=2 не подходит — что там за аргумент с углами?

Alexandroppolus
10.10.2021 02:05+2Что за суммарней угол тут считается? Если это про поворот вектора вдоль контура, то он, при всех a_i равных будет a, будет 2pia. Чем тут a=2 не подходит — я тоже непонимаю.
Там подразумевалось, что поезд, полностью объехав дорогу, должен повернуться на 360 градусов - т.е. на полный круг. Повернуться на N кругов (N > 1) он не может, тогда будут самопересечения пути. Потому добавленные детали должны дать в сумме нулевой поворот. Каждая деталь может дать либо 1/13 круга, либо -1/13 круга, то есть их должно быть четное количество - поровну плюсов и минусов.

vak0
08.10.2021 19:04+8Извиняюсь, если тут это не совсем уместно, но хочу поделиться старой (школьной) задачей, которую я считаю для себя лучшей, благодаря невероятно красивой постановке (минимум данных и при этом однозначное решение):
У некоторого султана было два мудреца: Али-ибн-Вали и Вали-ибн-Али. Желая убедиться в их мудрости, султан призвал мудрецов к себе и сказал: «Я задумал два числа. Оба они целые, каждое больше единицы, но меньше ста. Я перемножил эти числа и результат сообщу Али и при этом Вали я скажу сумму этих чисел. Если вы и вправду так мудры, как о вас говорят, то сможете узнать исходные числа».
Мудрецы задумались. Первым нарушил молчание Али.
— Я не знаю этих чисел, — сказал он, опуская голову.
— Я это знал, — подал голос Вали.
— Тогда я знаю эти числа, — обрадовался Али.
— Тогда и я знаю! — воскликнул Вали.
И мудрецы сообщили пораженному царю задуманные им числа.
Назовите эти числа.
MagisterLudi Автор
08.10.2021 19:10+3Класс!
Обожаю такие задачи, где еще и фигурирует «полнота информации» как переменная. Это наполовину арифметика, наполовину теория информации, наполовину что-то еще :)

GospodinKolhoznik
08.10.2021 19:39+2Ещё в чем то похожая на эту задача про кофе с молоком:
Вся семья выпила по полной чашке кофе с молоком, причём Катя выпила четверть всего молока и шестую часть всего кофе. Сколько человек в семье?
Тоже сначала кажется, что недостаточно информации для решения задачки.

vak0
08.10.2021 20:01+3У меня вот такое решение родилосьПусть объем кружки — 1, а объем кофе в Катиной кружке — х. Тогда молока у нее в кружке 1-х. Тогда общее количество кофе — 6х, а молока — 4(1-х). Общий объем жидкости — 6х+4(1-х)=2х+4. Поскольку х строго больше 0 и строго меньше 1, то 2х+4 приобретает целое значение только при х=1/2, а всего у нас получается 5 полных кружек. Но это все при условии, что кружки в семье одинаковые :)
Я думаю, эта задача существенно легче, чем про мудрецов, ту, я помню, в институте на протяжении целой пары решал.

dbalabanov
09.10.2021 10:16
mn3m0n1c_3n3m1
11.10.2021 11:49-4Что-то сложное решение у них получилось, мне кажется, что так быстро мудрецы могли бы только к такому прийти, но возможно я чего-то не учитываю. И так у нас два уравнения:
a + b = c a * b = dИ 4-ре неизвестных. Первый мудрец отметил, что не знает чисел, и второй сказал, что знал это. Конечно, пар чисел очень много, значит нужно упрощать:
a + a = c a * a = dТеперь у нас 3 неизвестных, два уравнения, и допущение, что султан загадал одинаковые числа. Дальше первый мудрец сказал, что теперь он знает, эти числа, то есть допустил, что c и d равны, тогда:
Решение
a + a = a * a;
2 = a*a/a
a = 2
К такому решению очень легко прийти, и это то что вполне могут выдать в процессе разговора мудрецы.
Читая существующие ответы возникает вопрос: для чего все эти усложнения, если мудрость в простоте.

BigBeaver
11.10.2021 12:43Но тогда бы они оба сразу знали ответ, тк 2 + 2 = 2 * 2 = 4 не допускает каких-либо толкований.

mn3m0n1c_3n3m1
11.10.2021 15:25-2Так они пришли к одному ответу обменявшись парой фраз, вряд ли они усложняли все с каждой фразой, скорее к общему знаменателю шли, понятному и очевидному, Keep it simply stupid.

valergrad
13.10.2021 12:15Ваше "решение" можно использовать как иллюстрацию к синдрому Даннинга-Крюгера.
Ошибка здесь:
"Дальше первый мудрец сказал, что теперь он знает, эти числа, то есть допустил, что c и d равны,"
"Знать" и "допустить" - совсем не одно и тоже. Мудрец сказал что знает эти числа только когда он смог однозначно их вычислить по имеющимся данным, безо всяких предположений.

Maxim_Q
08.10.2021 19:42Если можно будет использовать молоток и напильник то только 1 детальку нужно докупить.

vvmtutby
09.10.2021 16:30+1} молоток и напильник
Как проходивший "допуски и посадки", примерно за год до начертательной геометрии на 3-ем или 4-ом курсе ( код специальности - 22.04 ) и обладатель ГДР-овской железной дороги, возьму на себя смелость утверждать, что это излишне: паровозик повезёт три пассажирских вагончика даже "при расширенном диапазоне качества" строительных работ.
Отчасти, напоминает задачу из статьи Э.Дейкстры, любезно опубликованной в книге "Простое и сложное в программировании". И реакцию на ход её решения представителей разных профессий, в том числе "чистых математиков".

Tyusha
08.10.2021 19:42+1Негодная халтура!
Савватеев всё красочно рассказал. Если уж вы взялись подготовить текстовый вариант, то хотя бы разъясните решение, сделайте поясняющие рисунки в комплексной плоскости. Да хотя бы без ошибок перепишите из Ютуба решение! w = e^( 2π·i / 13). А вы даже не потрудились нормальную букву пи вставить!
Я в шоке, вроде @MagisterLudiнормальным автором всегда был.

iboltaev
08.10.2021 20:23о блин, я угадал решение, но на доказательство минимальности меня не хватило

edo1h
08.10.2021 21:34+1Напрашивается ответ а=2, но если мы посчитаем суммарный угол, на который повернулся наш вектор, то он должен быть нечетным, поэтому а=3
честно говоря, не понял

Arris
08.10.2021 21:34+3a0+a1w+a2w2+a3w3+a4w4+ a5w5+a6w6+a7w7+a8w8+a9w9+a10w10+a11w11+a12w12=0
А почему он так выглядит, автор материала может объяснить?
И что такое
w = e^( 2π·i / 13)
?
И почему?
P.S. Пост ради поста, да?

Galanit
08.10.2021 22:40Скажу честно, я бы эту задачу и сейчас с ходу не решил бы... тем более, школьником.

Megakazbek
09.10.2021 12:23А кто говорит про "сходу"? Хорошие задачи обычно решаются несколько месяцев. Для школьника это нормальный такой проект, в котором нужно заниматься исследованиями, прочитать несколько книжек и т.д.

agat000
09.10.2021 17:48Мне понравилась задачка про озеро. Мозг сломал, но решить смог только графически, логики не хватило. Как всегда, зная ответ кажется примитивной.

Alexandroppolus
09.10.2021 19:08Она интересна, если вместо 4 взять 4.6.
А вообще, полно таких задачек есть на braingames.ru

Alexandroppolus
12.10.2021 11:23+1Посмотрел видос, глянул комменты, нашел там ссылку , после этого стало понятно что к чему. В частности, откуда берется требование на одинаковые "а". Они могут быть разными, но тогда хотя бы одно из них будет иррациональное, а вот чтобы все были целыми - никак. Ну и всё прочее.

frobeniusfg
17.10.2021 16:02Насколько я понимаю, можно составить замкнутую "волнистую" кривую как в решении, взяв 3,5,7,9,11,13... сегментов и расположив из по принципу "один вверх, один вниз, один вверх...".
Для случая 13 у меня есть другая замкнутая конфигурация.
То есть элементов столько же, но расположены по-другому.



GospodinKolhoznik
4 детальки:
farafonoff
у вас дорога из четного числа сегментов, а в задании - из нечетного.
GospodinKolhoznik
Не прокатило (с)
mikhailian
Ндя, а было бы красиво
farafonoff
Круг из 13 сегментов нельзя разбить пополам как на фото. А круг из 8 - можно. Вопрос можно ли меньше чем 26 деталей интересен, но это фото совершенно точно не прокатило.
Alexandroppolus
Дело не в нечетности, а в том что 13 простое число. Если составное, берём максимальный делитель (пусть он равен Х), и к каждой Х-й детальке добавляем по две новые.
Будет ли это минимум - строго доказать пока не могу. Понятно только, что в любом случае добавить можно лишь четное количество деталей, половина из которых будут "минусы", т.е. перевёрнутые.
edo1h
почему максимальный? минимальный больший 1.
почему 1 не подходит надо подумать )
Alexandroppolus
Нет, именно максимальный. На картинке в первом комменте было 8 деталей, макс. делитель равен 4, каждую четвертую деталь (коих всего две штуки) утроили. А в задаче 13 деталей, там макс. делитель равен 1, и потому устраиваем каждую первую, то есть все.
MinimumLaw
Да, задачи надо четко формулировать. Особенно математикам. Стоило в вопросе пропустить "кольцевую" и... Решение в корне меняется. Браво.
dmlogv
Задачка в стиле ТРИЗ, когда у автора изобретения немного побольше информации, чем у читающего книгу :)
WASD1
спасибо за хорошую формулировку.
Меня как-то убидили почитать ТРИЗ - и всё время чтения чувствовал, что
меня неё...что-то не так, но сформулировать кроме как "фигня какая-то" не мог.Aleksandr-JS-Developer
Этот как читаешь книгу про детектива и думаешь, кто убийца. А потом, в самом конце всплывает какой-нибудь факт, который знал только сыщик и этот факт ставит всё на свои места. Очень раздражает...
nochkin
Если чётко формулировать, то надо бы уточнить, что речь про минимальное дополнительное количество. Иначе ответов много.
extempl
Почему тогда не 8?
4 - ответ для "сколько еще, минимум, таких элементов надо докупить". Я вот сразу подумал про бесконечное, потому что "более длинную" прочитал как "максимально длинную".
Но да, как уже указали, пропущено ещё одно слово - "кольцевую".
MagisterLudi Автор
замкнутую = «кольцевую», только более корректно