Краткий рассказ про пакет MVN
Минутка теории
Допустим, у нас есть некоторое совместное распределение n переменных – и нам необходимо проверить, является ли оно нормальным. Решить эту задачу просто нам мешает один маленький факт – из нормальности многомерного распределения следует нормальность распределения каждой переменной в отдельности, но в обратную сторону это работает только при случае независимости компонентов распределения, что на практике не выполняется почти никогда. Поэтому приходится что-то изобретать.
Схема проверки статистической гипотезы о нормальности многомерного распределения идентична соответствующей для одномерного случая, только в ней используются другие тесты.
Тест Мардиа (оригинальная работа: K. V. Mardia. Measures of multivariate skewness and kurtosis with applications. Biometrika, 57(3): 519–530, 1970) основан на вычислении эксцесса и асимметрии многомерного распределения по формулам

При этом m – это расстояние Маланхобиса между i-м и j-м наблюдениями
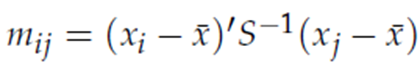
В такой трактовке рассчитанная величина асимметрии, умноженная на n/6, распределена по закону Хи-квадрат с p(p+1)(p+2)/6 степенями свободы, а величина эксцесса распределена по закону нормального распределения со средним p(p+2) и отклонением 8p(p+2)/n
Тест Хенце-Циклера (базовая работа: N. Henze and B. Zirkler. A class of invariant consistent tests for multivariate normality. Communications in Statistics - Theory and Methods, 19(10):3595–3617, 1990.) основан на следующей формуле расчета статистического критерия:

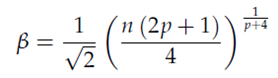
Значения критерия распределены по логнормальному закону с параметрами
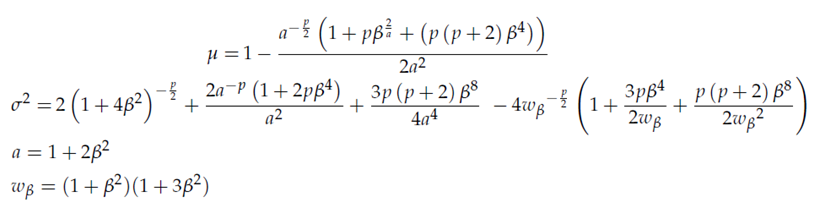
Тест Ройстона основан на идее теста Шапиро-Уилкса. Значение статистического критерия рассчитывается по формуле
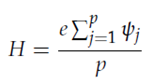
Его величина распределяется по закону Хи-квадрат с количеством степеней свободы, равным е. Цепочка расчетов следующая:

Тест Дорника-Хансена (оригинальная работа: Doornik, J. A., and H. Hansen. 2008. An omnibus test for univariate and multivariate normality. Oxford Bulletin of Economics and Statistics 70: 927–939.) основан на преобразовании многомерных наблюдений и вычислении эксцесса и асимметрии для одномерной переменной.
Преобразование проводиться по формуле
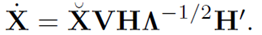
Далее рассчитывается эксцесс и асимметрия для каждой переменной в новой матрице.
Значения асимметрии (b1) и эксцесса (b2) распределены не по нормальному закону. Для их трансформации применяются следующие преобразования:
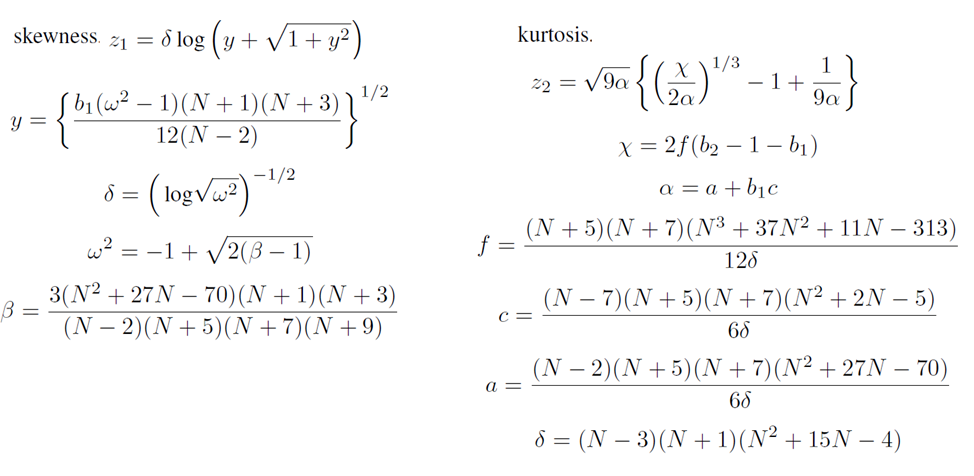
Полученные значения z1 и z2 объединяются в вектора Z1 и Z2, а рассчитанная величина статистики распределена по закону Хи-квадрат с числом степеней свободы, равном 2k

Тест Е-статистики (тест Шекели-Риццо, базовая работа: G.J. Szekely, M.L. Rizzo. A new test for multivariate normality / Journal of Multivariate Analysis 93 (2005) 58–80) подразумевает вычисление тестовой статистики с помощью разложения в ряд Тейлора:
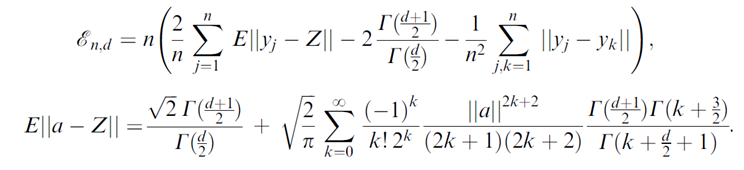
y – центрированная матрица наблюдений, получаемая путем постолбцовых пребразований как
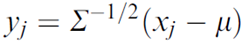
Методология
Для примера выберем базу данных “Crime” из пакета plm, и возьмем оттуда три переменных:
prbpris – вероятность тюремного заключения
avgsen – средний срок заключения, дней
pctymle – доля в населении мужчин в возрасте 15-24 лет
Из этих трех переменных соберем две базы данных – с двумя и тремя переменными:
library(MVN)
library(tidyverse)
library(plm)
data("Crime")
glimpse(Crime)
ggplot(Crime, aes(x=Crime$avgsen)) + geom_density()
# Crime$prbpris - точно, avgsen - 70/30, pctymle - 50/50
Data_1 <- Crime[,c(6,7)]
Data_2 <- Crime[,c(6,7,24)]Расчеты и описание
Базовая функция расчетов – функция mvn со следующими параметрами:
data - База данных (в виде матрицы или датафрейма)
subset - Факторная группировочная переменная
mvnTest - Определяет статистический тест, которым проводится проверка
desc - Логическая переменная. Если она равна истине, выводятся описательные статистики
univariateTest - Определяет статистический тест, которым проводится проверка на нормальность отдельных переменных
univariatePlot - Определяет вид выводимого одномерного графика нормальности
multivariatePlot - Определяет вид графика ошибок
multivariateOutlierMethod - Выбирает метод определения выбросов
Проверим наши данные на нормальность с помощью классического теста Мардиа
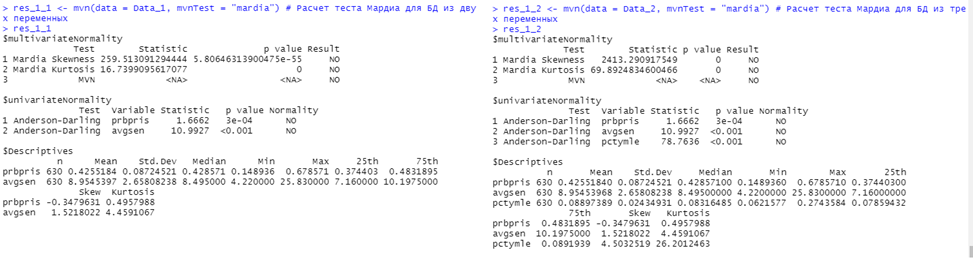
Можно глазами посмотреть на Q-Q график
mvn(data = Data_1, mvnTest = "mardia", multivariatePlot = "qq")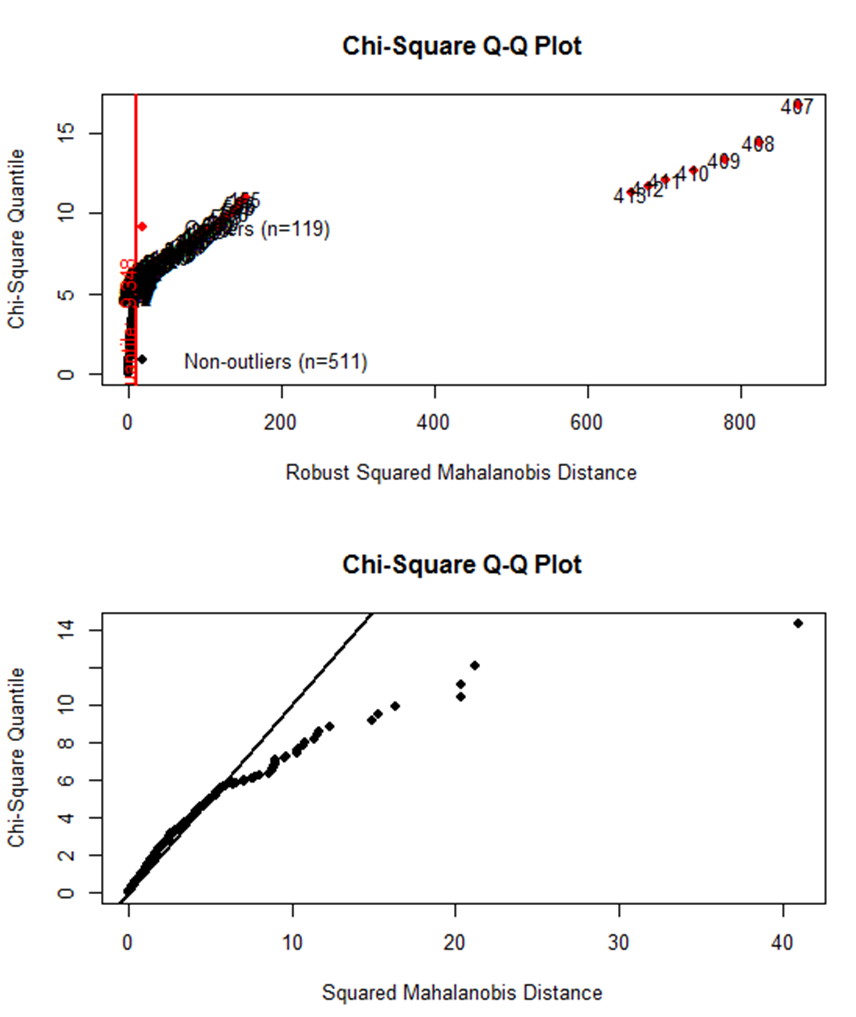
А также на двумерный график распределения
mvn(data = Data_1, mvnTest = "mardia", multivariatePlot = "qq")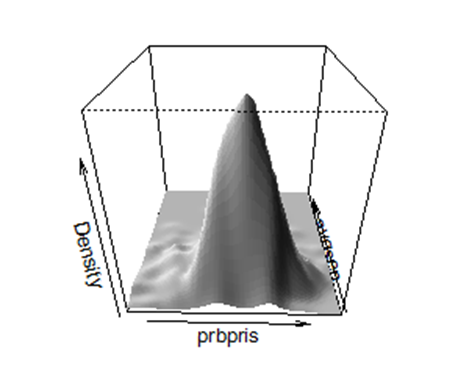
И на двумерный контурный график
mvn(data = Data_1, mvnTest = "energy", multivariatePlot = "contour")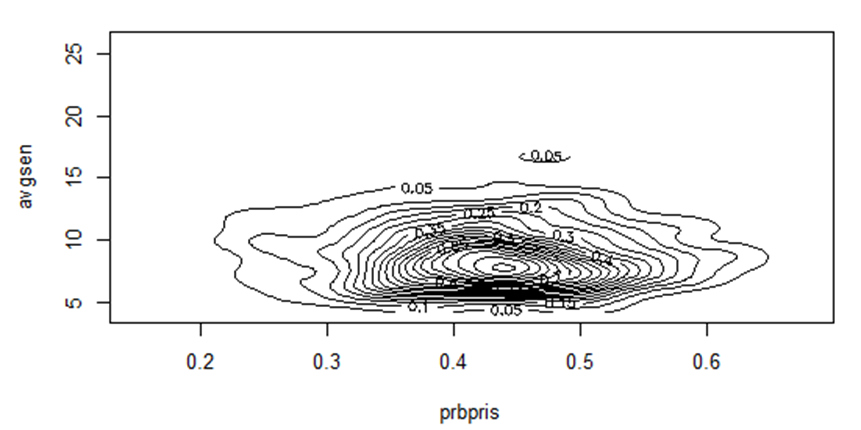
Можно также вывести, например, Q-Q график по каждой переменной в отдельности
mvn(data = Data_1, mvnTest = "mardia", univariatePlot = "qqplot")Особенно интересна возможность, предоставляемая переменной subset. Если есть группировочная переменная, есть возможность проверить многомерные / одномерные нормальности в зависимости от разных ее значений:

Это основы функционала пакета MVN. Все материалы доступны на https://github.com/acheremuhin/Multivariate_normal


victor_1212
Привет Артем, что у вас за терминал или принтер стоит (ностальгию почувствовал увидев последнюю картинку) ?
И для каких (функциональных) применений пакет предназначен ?
acheremuhin Автор
Добрый день, Виктор. Что касается ностальгии по последней картинке - это результат симбиоза PrintScreen и Point. Насчет же функционального применения - любая область, в которой вам нужно проверить наличие многомерного нормального распределения. Как правило, в предобработке данных, поскольку некоторые методы анализа в качестве условия требуют именно это условие.
victor_1212
> любая область, в которой ...
Спасибо Артем, насколько полезным этот пакет покажет себя именно на конкретных проблемах вот вопрос, достаточно знаю теорию вероятностей чтобы понимать вас с полуслова, но правильная интерпретация результатов это своего рода искусство, и это для меня самое интересное :)