Лабиринты на сегодняшний день всё ещё важны в развлекательной сфере. И это не только зеркальный лабиринт в парках аттракционов, но и видеоигры, ведь если посмотреть на карты и уровни в различных играх, то это всё один большой и сложный лабиринт, построенный по некоторым правилам.

А что если мы хотим тоже сделать свой интересный и уникальный лабиринт? Очевидно, нужно создать эти самые правила. Далее я постараюсь кратко, понятно и без лишних непонятных букв рассказать о разработке своего подхода к генерации различного рода лабиринтов. Объясню, почему я этим занялся, с чего начинал и как всё развилось до вполне приличного алгоритма на основе подхода и почему каждый из вас может взять этот подход за основу и адаптировать его под свои желания.

▍ Небольшое лирическое предисловие

Предыстория: почему же так получилось, и как же я дошёл до того, что буду описывать далее. Когда-то давно, во времена старших классов в школе, я разрабатывал модификацию на движке Source, которая, увы, релиза своего не увидела (но возможно у меня хватит желания и смелости продолжить всё уже на UE). Но дала небольшой опыт в игровой индустрии, а также тему для дипломных работ и научных статей.


Изначально при проектировании одного из уровней возникла задачка из разряда комбинаторики: есть определённый уровень, построенный из большого числа коридоров, есть различные препятствия в виде силовых полей и турелей, есть разные кабинеты (открытые и закрытые), вентиляция между ними и прочие моменты. Задача была на словах предельно ясна — расположить все эти компоненты так, чтобы получить хорошую вариативность прохождения уровня и исключить возможность появления «читерного» сокращения. Задача максимум — сделать так, чтобы на уровне при каждой загрузке генерировался уникальный набор вышеперечисленных юнитов (на самом деле даже древний source, если сильно напрячься с реализацией, мог делать подобие процедурной генерации).

Каким образом такая задача переросла в проект с генератором лабиринта — сказать сложно. Но то, что всё разрослось в хороший такой комплекс — это факт. Оговорюсь заранее, что на протяжении всей разработки не рассматривался довольно современный и эффективный вариант в лице нейронок, и это было сделано намеренно, дабы постараться выжать хорошие результаты из вполне классических методов и алгоритмов.

▍ Задача генерации лабиринта

Если быть кратким, то первоначальная задача была такова: разработать алгоритм, генерирующий лабиринт с (обязательно!) несколькими проходами (их число желательно бы тоже задавать до генерации), которые были бы примерно равны по своей длине и не создавали какие-либо слишком короткие варианты прохождения. При этом вход и выход из лабиринта имеются в количестве только одной штуки.

Если вы начнёте погружаться в тему генерации лабиринтов, то, в общем и целом, найдёте там интересные вещи. Типизация лабиринтов с кучей категорий, клеточные автоматы, рандомные комнаты, алгоритмы генерации и прохождения лабиринтов, подробности об их положительных и отрицательных сторонах. Но если проанализировать всю информацию, то можно заметить, что почти вся она посвящена лабиринтам с одним проходом. Те немногие рассуждения, касающиеся лабиринтов с несколькими проходами, обычно довольно просты и не рассматривают какие-то сложные конструкции алгоритма.

Вся разработка поделилась на два этапа, и самый интересный — второй. Но про первый всё равно придётся вкратце рассказать. Для полноты картины, так сказать.

▍ Первый (и неинтересный) вариант генерации лабиринта

Первые шаги в построении нового алгоритма были довольно примитивными. Для начала, исходя из материалов данного сайта, был выбран базовый алгоритм построения лабиринта — алгоритм Уилсона. Он довольно прост в реализации и понимании, но главное — довольно быстрый, не имеет тенденций делать похожие лабиринты, а также гибок в настройке. То есть даже если ограничить область лабиринта не прямоугольным полем, а в виде буквы «Г», то алгоритм прекрасно сработает.

Как работает алгоритм Уилсона наглядно:



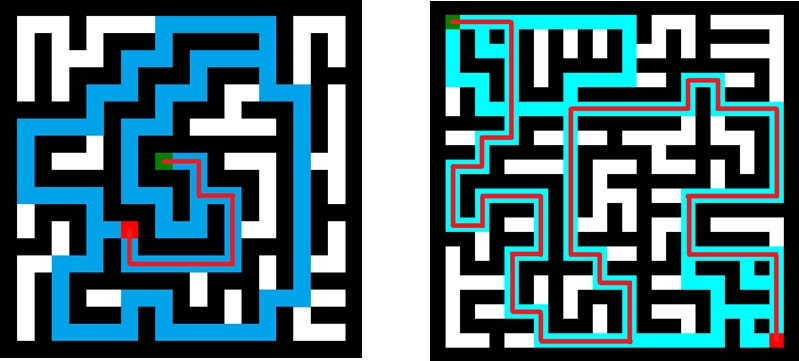
Именно такое свойство было базой для первого варианта алгоритма. Прямоугольное поле для лабиринта разделяется на три области: среднюю (1), внутреннюю (2) и внешнюю (3). В каждой из них генерируется лабиринт алгоритмом Уилсона (в средней части со своими особенностями) отдельно. А после этого достаточно сделать два и более прохода между внешней и средней областью. Картинка ниже наглядно показывает весь процесс.

Та генерация, которая «неинтересная»:



Формально мы получаем лабиринт с двумя и более проходами, а количество проходов зависит только от того, сколько точек доступа мы сделаем между средней и внешней областью. Более того, даже по длинам путей всё получалось более-менее прилично. Но всё же, есть существенные недостатки. Например, очевидно то, что все пути обязательно будут проходить через центральную его часть, или же то, что вход и выход из лабиринта обязаны быть на крайних точках, причём в противоположных сторонах. Вдобавок, алгоритм не рассчитан на построение маленьких лабиринтов, то есть сгенерировать мини-лабиринт 10x10 «толстых» клеток у нас не получится. В конце концов, слабо контролируется число пересечений путей, а также визуально выделяются длинные стенки между внешней и средней областью.

Если интересно что такое тонкие и толстые клетки:



Несмотря на не самый красивый результат, алгоритм всё же есть в наличии. Теперь было бы неплохо прикрутить к нему поиск получаемых путей. И здесь тоже встал вопрос эффективного их нахождения. Ведь если почитать про все алгоритмы нахождения путей в лабиринте, то ни один из них не даёт гарантий в нахождении абсолютно всех путей. Какие-то рассчитаны только на один, какие-то могут пропустить «пару-тройку». Поэтому и здесь пришлось разрабатывать новое.

По итогу за основу был взят самый обыкновенный муравьиный алгоритм, но с некоторыми изменениями в «концепции». Один за другим, муравьи ищут новые пути. Один муравей равен одному возможному пути. «Возможному» означает, что по достижении выхода путь текущего муравья будет сравниваться с уже имеющимся на предмет повторения. Каждый муравей рассматривает до четырёх возможных направлений (все 4 могут быть, например, в точке старта).

Куда может ходить муравей:



Следующее и основное изменение заключается в использовании феромонов. Во-первых, они будут использоваться только на развилках. Во-вторых, было убрано испарение феромонов. В-третьих, сам расчёт феромонов, представляющий из себя вероятность выбрать то или иное направление, преследует цель увеличения вероятности для нового муравья выбирать менее популярный путь, дабы быстрее находить новые вариации прохождения. В дополнение к этому, тупиковые ветки автоматически обнуляли вероятность такового направления, а также был проработан случай зацикливания муравья на своём же пути. Далее был проведён эксперимент с целью найти оптимальное количество муравьёв для любого варианта лабиринта. Как уже было упомянуто, зависит оно от числа тех вырезов, которые мы сделали в конце алгоритма. Конечно, оптимальные цифры не самые приятные, муравьёв требуется немало, но зато это гарантированное нахождение всех путей (ну почти, при 8 вырезах уже есть небольшой шанс потерять пару путей, поэтому было рекомендовано использовать цифры 2, 4 и 6).

Много цифр! Результаты эксперимента (к первому столбцу прибавляем 2):



И уж чтобы закончить первую часть, пару слов о том, что к алгоритму были добавлены небольшие утилиты, которые пробовали удалять, например, слишком длинные или короткие пути, а также пути, совпадающие на некоторую часть. Их эффективность была около 50%, потому что редактировать уже построенный лабиринт непросто, поэтому сильными средствами редактирования лабиринта их точно не назовёшь.

Итого, первая часть закончена, решение получено, пусть оно громоздкое и неказистое.

▍ Второй вариант генерации лабиринта

Теперь часть вторая, более увлекательная. Естественно, у текущего алгоритма полно недостатков, которые надо исправлять. И нужно это делать либо продолжая модифицировать текущий вариант, либо придумывая новую концепцию. Первый вариант быстро отпал, потому как требовал много изменений кода. Да и добавляя новое, необходимо отлаживать и проверять, чтобы ничего уже работающее не сломалось. А второй, естественно, требовал придумать более выгодный алгоритм.

И идея для него родилась непосредственно из алгоритма поиска путей: а что если использовать именно алгоритм на базе муравьиного? Более того, следом за этой мыслью пришла другая — а может строить лабиринт наоборот? Сначала пути, а потом тупиковые ветви. Во-первых, это избавит от дальнейшего поиска путей, а во-вторых, можно вносить коррективы в лабиринт по мере его генерации. Более подробную информацию о подходе, выведенных формулах и тестировании можно прочитать в моей статье, которая, (возможно) к сожалению, только на английском языке. Здесь же я хочу рассказать на более простом и понятном языке основные моменты, без разбора громоздких формул (а финальная вероятностная формула получилась довольно большой).

Теперь вся идея, описанная для нахождения путей через модифицированный муравьиный алгоритм, будет работать в обратную сторону. Оттого и назван метод обратным. Всё так же у нас выбирается вероятность выбрать ту или иную клетку лабиринта. Всё так же мы уменьшаем вероятность выбрать клетку, по которой уже до этого проходили другие муравьи. Более того, добавим ещё и подслой лабиринта, в котором содержится количество посещений каждой клетки всеми муравьями. Соответственно, чем больше прошло до нас муравьёв по возможной следующей клетке, тем охотнее текущий муравей от неё откажется. Таким образом, мы убьём двух зайцев — и путь построим более уникальный, и минимизируем число пересечений путей.

С таким подходом у нас появляются дополнительные возможности. Мы можем в любой момент отследить количество пройденных клеток, то есть строить пути определённой длины (или близкой к некоторому числу). Число данное мы можем либо вводить, что не совсем корректно, так как пользователь не может без дополнительных расчётов понимать каким оно может быть и каким быть не должно. Либо же автоматически высчитывать эту длину исходя из размеров лабиринта. Добавим к вычисленному значению некоторую дельту, допустим, длина пути минус 2 клетки. И теперь мы знаем сразу и количество пройденных клеток, и необходимую длину пути, что даст нам возможность влиять на его дальнейшее построение.

Вариант влияния довольно прост — мы будем стараться «отводить» муравья подальше от выхода, если он ещё не «нашагал» нужное число клеток и, наоборот, быстрее подводить муравья к нему, если муравей уже близок к нужной длине пути. На деле же мы столкнёмся с тем, что путь муравья может быть очень извилистым в начале и слишком прямым в конце или же наоборот (чуть позже будет картинка, иллюстрирующая это). К счастью, эксперименты показали, что этот момент можно отрегулировать и получить сбалансированную извилистость пути.

Несмотря на минимизацию количества пересечений, сами по себе пересечения никуда не исчезают. Они могут быть случайными (рандом так решил) или вынужденными (когда другие направления не приводят к нужному результату). Поэтому при каждом пересечении нового пути с уже существующим, необходимо проверять, не образует ли такое пересечение новый очень короткий путь. Делаем это просто суммируя пройденный текущий путь со всеми новыми вариантами, которые он образует, и сравнивая с нашей необходимой длиной.

Может возникнуть и такая ситуация, что все варианты направлений не подойдут. Например, все ведут к тупиковой ситуации или же дают недопустимое пересечение. Тогда необходимо выполнить откат до предыдущей точки, временно запретить выбирать ту, из которой мы откатились, и начать процедуру выбора направления заново.

▍ Про то, как сделать уникальный тип лабиринтов

Все эти действия натолкнули на создание некоторого рода «правил правильного лабиринта». То есть, предположим, мы хотим, чтобы:

1. Пути нашего лабиринта были достаточно «извилистыми».
2. У лабиринта было как можно меньше пересечений.
3. Не было нечестного короткого пути.
4. Построенные пути максимально эффективно использовали поле лабиринта.

Немного пояснений. Под извилистостью путей понимается то, насколько часто меняется направление при построении пути. Если алгоритм выбрал одно и то же направление, к примеру, десять раз подряд — такой путь станет проще для прохождения. Однако не забываем, что мы привязаны к желаемой длине пути, поэтому делать длинную «змейку» тоже не получится.

Например, на рисунке ниже представлены различные варианты лабиринтов разных размеров. И довольно отчётливо можно заметить, что «витиеватость» лабиринтов из верхней строки ниже, чем из второй, особенно на больших размерах.

Пример:



По количеству пересечений необходимо упомянуть только то, что мы стараемся всего лишь сократить их количество. Совсем избавиться от пересечений не получится. Пример ниже как раз показывает тот факт, что в некоторые моменты без пересечений не получится построить дальнейшие пути.

Почему без пересечений нельзя:



Также при обработке пересечений учитываем возможное появление нечестных коротких путей. Однако, что касается получаемых от пересечений очень длинных путей, их мы не трогаем. Такие пути, очевидно, будут появляться.

Про читерство (осуждаем):



Последний пункт тоже проиллюстрируем. Необходимо стараться использовать всю данную площадь. Объясняя на примерах — только в правом нижнем варианте максимально эффективно используется поле лабиринта.

Про эффективность поля:



Бонусом всего этого является, наконец, возможность свободного выбора входа и выхода в лабиринт. То есть, даже расположив вход и выход на соседних клетках, мы получим правильный лабиринт с необходимой минимальной длиной путей.

▍ Чем подход интересен и какие у него подводные камни

В теории — уникальный интересный алгоритм, который может много чего учитывать. На практике же — требуются небольшие уточнения и доработки. Например, правила правилами, но всемогущий рандом может от них отклониться. При большом количестве генераций подряд действительно правильными (в пределах принятых правил) выходили далеко не все. В основном дело касалось пересечений (большое их количество и появление «зала с колоннами») и использованию пространства (все же оставались неиспользованные и, наоборот, нагромождённые путями, области).

Примеры изъянов:



В целом, можно по-разному попытаться всё решить. Например, довольно интересно было бы посмотреть, какова была бы ситуация, будь у нас аппаратный генератор случайных чисел вместо псевдослучайных. Или же попробовать добавить дополнительных регуляторов, завязанных на каких-то данных.

Метод, использованный мною, оказался достаточно эффективным по получаемым результатам, но, к сожалению, не самый эффективный по времени работы. Были введены колонии. То есть, после получения первого пути, для дальнейших итераций алгоритма генерировалось некоторое количество вариантов путей, после чего из всех выбирался один наилучший. Экспериментально было выявлено, что 20 вариантов достаточно, чтобы один из них был наилучшим. В качестве критериев оценки — наши «правила правильного лабиринта», переведенные в цифры. Количество смен направлений и пересечений считать не надо даже. А вот эффективное использование поля — это, так сказать, поле для размышлений. Я остановился на следующем варианте: Для каждого i-го пути из колонии возможных новых путей считаем сумму расстояний j-й клетки этого пути и j-й клетки остальных уже построенных путей. Остатки более длинного пути можно просто не трогать. Пожалуй, здесь было бы понятнее объяснить процесс формулой:

где — множество уже построенных путей,
— минимум из длин i-го пути колонии и t-го пути из уже построенных,
— j-я клетка i-го пути из колонии,
— j-я клетка t-го пути из множества

Но уверен, что есть и более эффективный вариант просчитать, насколько один путь проходит далеко от другого. Далее критерии суммируются, и путь с наилучшим критерием добавляется.

Из других компонентов, которые возможно улучшить. Пока что нет эффективного контроля результирующего числа проходов. То есть в программе мы указываем лишь количество итераций алгоритма построения пути. А дальше, накладываем пересечения (которые минимизируются, не забываем) и получаем + несколько путей. С другой стороны, здесь возникают некоторые вопросы, которые могут иметь несколько ответов. Допустим, возьмём лабиринты из картинки выше. В них есть совсем небольшие разветвления. Считать ли их однозначно проблемой, из-за которых появляется много новых путей? Сложно сказать. Технически да, психологически для игрока не сильно.

Изрядную часть времени съедают колонии, поэтому более эффективная по времени генерация качественных лабиринтов тоже необходима.

После того как мы построили все пути, у нас остаётся неиспользованное место на поле под тупиковые ветви. И здесь нам снова помогает наш друг — алгоритм Уилсона. Помечаем клетки, через которые проходят пути, как помеченные, остальные как непомеченные. Запускаем алгоритм — и вуаля, тупики построены. Ну а примеры построенных лабиринтов вы могли наблюдать на картинках во время чтения этой статьи.

▍ Выводы

Итого, всё вышеописанное представляет собой целую модульную конструкцию. У нас есть модификация муравьиного алгоритма, способная строить путь от входа к выходу. А далее мы просто добавляем к нашей основе различные модули, представляющие из себя некоторые правила. Представленные в данной статье правила — лишь один из возможных вариантов. Такой подход более гибкий, нежели первый, и позволяет сочетать различные желаемые правила и получать уникальные типы лабиринтов. Естественно, метод не доведён до идеала. Например, можно ещё улучшить использование незанятого пространства, добавив проверку некоторой небольшой области перед муравьём на наличие большого количества других путей в ней. А также можно уточнить работу с пересечениями, добавив остановку алгоритма по достижении некоторого количества путей, чтобы получать конкретное общее количество путей вместо некоторого «интервала возможных путей».

Для более подробного ознакомления со всей разработкой есть три моих статьи:


К слову о программе. Я долго размышлял, стоит ли её показать, очень не хотелось, потому что до релиза ей далеко, у неё много багов, недоработок, хотя с генерацией небольших лабиринтов она справляется хорошо (лично у меня после разных проверок нашлись странные моменты, которые раньше работали, а сейчас почему-то нет, возможно, из-за Win11). Но я всё же выложу её здесь и буду стараться потихоньку исправлять баги и дорабатывать её.

Если же скачивать и пробовать чужую кривую прогу не хочется, то есть короткий ролик, демонстрирующий основные функции программы: генерация лабиринта с разными характеристиками, рисование лабиринта на поле «своими руками» и прохождение 2D/3D лабиринта.

Видео-демонстрация: