Мы продолжаем нашу серию статей, связанных с байесовскими методами, один из которых — Байесовские Сети Доверия (БСД). Теоретическую основу БСД вы можете найти в этой статье.

В этой статье мы сначала вкратце вспомним теорию. Дальше будет, что называется, только хардкор: на примере данных “Титаника” мы будем строить БСД.

Теория

Методы по теореме Байеса

Существует множество методов, основанных на теореме Байеса, но в конечном итоге все они сводятся к одной простой формуле (рис.1)

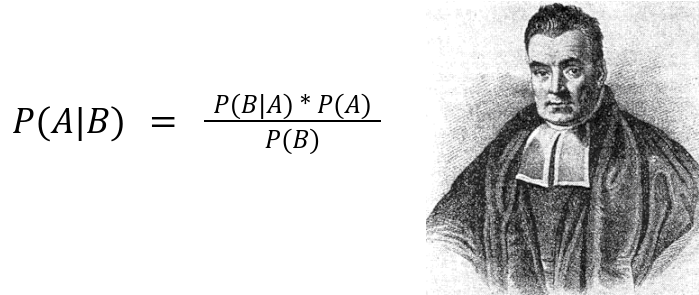
[Вероятность возникновения события A, если есть событие B] равна [вероятности возникновения события A] умноженной на [вероятность возникновения события B при условии существования события A], деленную на [вероятность события B]

Иначе говоря, у нас есть некая гипотеза (А), но в ней появилось некоторое новое условие (В). Нам нужно узнать вероятность А при условии В (P (B | А) / Р (В)). Для этого мы берем статистические данные в процентах (по событию А и по событию В) и подставляем их в эту формулу.

Использование байесовского анализа: пример с погодой

Это изображение может помочь понять, как работает простая байесовская модель.

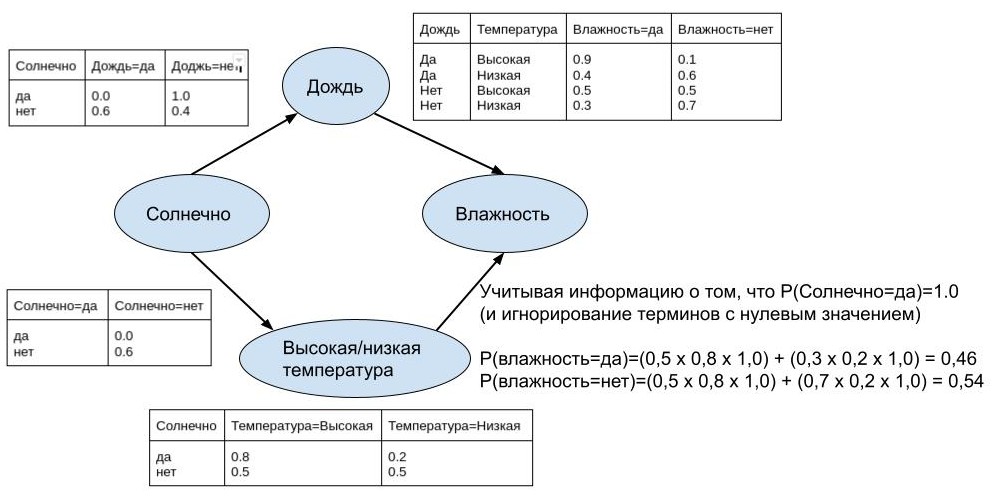
• Учитывая, что у нас есть события солнца, дождя и высокой/низкой температуры, и мы хотим предсказать, будет влажно или нет, вероятность наличия влажности будет рассчитываться на основе других заданных событий и их вероятностей.

• В полях у нас есть «солнечно» как независимое событие, «дождь» и «высокая/низкая температура» как события, зависящие от «солнечно», и, наконец, «влажность», зависящая от всех остальных.

• В тексте, расположенном в правом нижнем углу схемы, задана вероятность влажности, при этом учитывается, что если солнечность равна 100%, вероятность исхода “влажно=да” = 46%, а исхода “влажно=нет” = 54%.

Основываясь на предыдущем примере, мы попробуем смоделировать ситуацию с предсказанием прогноза погоды, чтобы закрепить наши теоретические знания на практике.

1. Предположим, что синоптики оценили вероятность дождя на завтра в 30%.

2. Вероятность облачности в этот день они оценили в 50%.

3. Мы также знаем, что вероятность облачности в случае дождя составляет 100% (облака всегда есть во время дождя).

У нас есть следующие данные:

• P (A) = вероятность дождя = 30%

• P (B) = вероятность облаков = 50%

• P (B | A) = вероятность облачности в дождь = 100%

Вы просыпаетесь утром и получаете новую информацию — на небе сейчас облака. Теперь вы можете применить теорему Байеса, чтобы повторно проанализировать вероятность дождя в данный день.

Вспоминаем уравнение: P (A | B) = P (A) * P (B | A) / P (B) = [вероятность дождя] * [вероятность облаков во время дождя] / [вероятность облаков в целом] = 30% * 100% / 50% = 60%.

Теперь с учетом новых данных мы пересмотрели свой прогноз вероятности дождя – он увеличился с 30% до 60%.

Теперь определим, что такое БСД.

БСД представляют собой основу для рассуждений в условиях неопределенности с использованием вероятностей. Более формально БСД определяются как направленный ациклический граф (именно так на практике моделируется проблемная область) и набор таблиц условной вероятности.

Практика

Для того, чтобы применить полученные знания, построим БСД на наборе данных “Титаника”.

Для этого загрузим необходимые библиотеки

import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats.stats import pearsonr
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score

%matplotlib inline
# Скрыть предупреждения
warnings.filterwarnings("ignore")

Определим функцию для кросс-валидации. С использованием кросс-валидации мы улучшим обобщающие способности алгоритмов.

def cross_validate(estimator, train, validation):
    X_train = train[0]
    Y_train = train[1]
    X_val = validation[0]
    Y_val = validation[1]
    train_predictions = classifier.predict(X_train)
    train_accuracy = accuracy_score(train_predictions, Y_train)
    train_recall = recall_score(train_predictions, Y_train)
    train_precision = precision_score(train_predictions, Y_train)

    val_predictions = classifier.predict(X_val)
    val_accuracy = accuracy_score(val_predictions, Y_val)
    val_recall = recall_score(val_predictions, Y_val)
    val_precision = precision_score(val_predictions, Y_val)

    print('Model metrics')
    print('Accuracy  Train: %.2f, Validation: %.2f' % (train_accuracy, val_accuracy))
    print('Recall    Train: %.2f, Validation: %.2f' % (train_recall, val_recall))
    print('Precision Train: %.2f, Validation: %.2f' % (train_precision, val_precision))

Загрузим данные с условием, что они уже разделены на тренировочные и тестовые и выложены в указанный путь в коде.

train_raw = pd.read_csv('../input/train.csv')
test_raw = pd.read_csv('../input/test.csv')
test_ids = test_raw['PassengerId'].values

#  Соединим данные, чтобы проанализировать и обработать набор как единое целое.
train_raw['train'] = 1
test_raw['train'] = 0
data = train_raw.append(test_raw, sort=False)

Одно из преимуществ БСД заключается в том, что они достаточно хорошо работают с небольшим количеством данных, а увеличение их количества даст вам более точные результаты. Но БСД не нуждаются в многочисленных данных, в отличие от глубокого обучения (англ. deep learning).

Предварительная обработка данных

Выполним нижеперечисленные манипуляции:

• Очистку данных. Она выполняется над определенными выборками в базах данных или файлах. Необходимость в очистке чаще всего возникает при интеграции различных информационных систем.

• Отбор признаков, также известный как отбор переменных, отбор атрибутов или отбор предикторов. В редких случаях генерализация — это разновидность абстрагирования, процесс отбора подмножества значимых признаков (как зависимых, так и независимых переменных) для построения модели.

• Feature engineering. Предусматривает превращение данных, специфических для предметной области, в понятные для модели векторы.

• Импутацию данных. Работа с отсутствующими значениями –  одна из самых сложных и вместе с тем самых распространенных проблем очистки. Большинство моделей не предполагает пропусков.

features = ['Age', 'Embarked', 'Fare', 'Parch', 'Pclass', 'Sex', 'SibSp']
target = 'Survived'

data = data[features + [target] + ['train']]
# Категориальные значения преобразуем в числовые.
data['Sex'] = data['Sex'].replace(["female", "male"], [0, 1])
data['Embarked'] = data['Embarked'].replace(['S', 'C', 'Q'], [1, 2, 3])
data['Age'] = pd.qcut(data['Age'], 10, labels=False)

# Разделим данные на обучающие и тестовые выборки.
train = data.query('train == 1')
test = data.query('train == 0')

# Удалим null значения из тренеровочных набора данных.
train.dropna(axis=0, inplace=True)
labels = train[target].values

Нижеприведённая таблица представляет собой часть обработанных данных.

train.head()

Корреляционное исследование

БСД предполагают, что features (так называемые признаки переменных) будут независимыми, поэтому применим к ним коэффициент корреляции Пирсона. Это даст нам подсказку о том, насколько эти признаки независимы друг от друга.

columns = train[features + [target]].columns.tolist()
nColumns = len(columns)
result = pd.DataFrame(np.zeros((nColumns, nColumns)), columns=columns)

# Применим корреляцию Пирсона к каждой паре признаков.
for col_a in range(nColumns):
    for col_b in range(nColumns):
        result.iloc[[col_a], [col_b]] = pearsonr(train.loc[:, columns[col_a]], train.loc[:,  columns[col_b]])[0]
        
fig, ax = plt.subplots(figsize=(10,10))
ax = sns.heatmap(result, yticklabels=columns, vmin=-1, vmax=1, annot=True, fmt='.2f', linewidths=.2)
ax.set_title('PCC - Pearson correlation coefficient')
plt.show()

Что касается корреляции между функциями, мы видим, что «Fare» и «Pclass» кажутся тесно связанными, поэтому уберем «Pclass». Также хорошими предикторами должны быть такие функции, как «Sex», «Pclass» и «Fare».

Исследование распространения

Модель ожидает, что функции будут распределяться в соответствии с теоремой Гаусса, однако распределение данных может быть ненормальным. По этой причине будет целесообразным проверить метод функционального распределения.

continuous_numeric_features = ['Age', 'Fare', 'Parch', 'SibSp']
for feature in continuous_numeric_features:
    sns.distplot(train[feature])
    plt.show()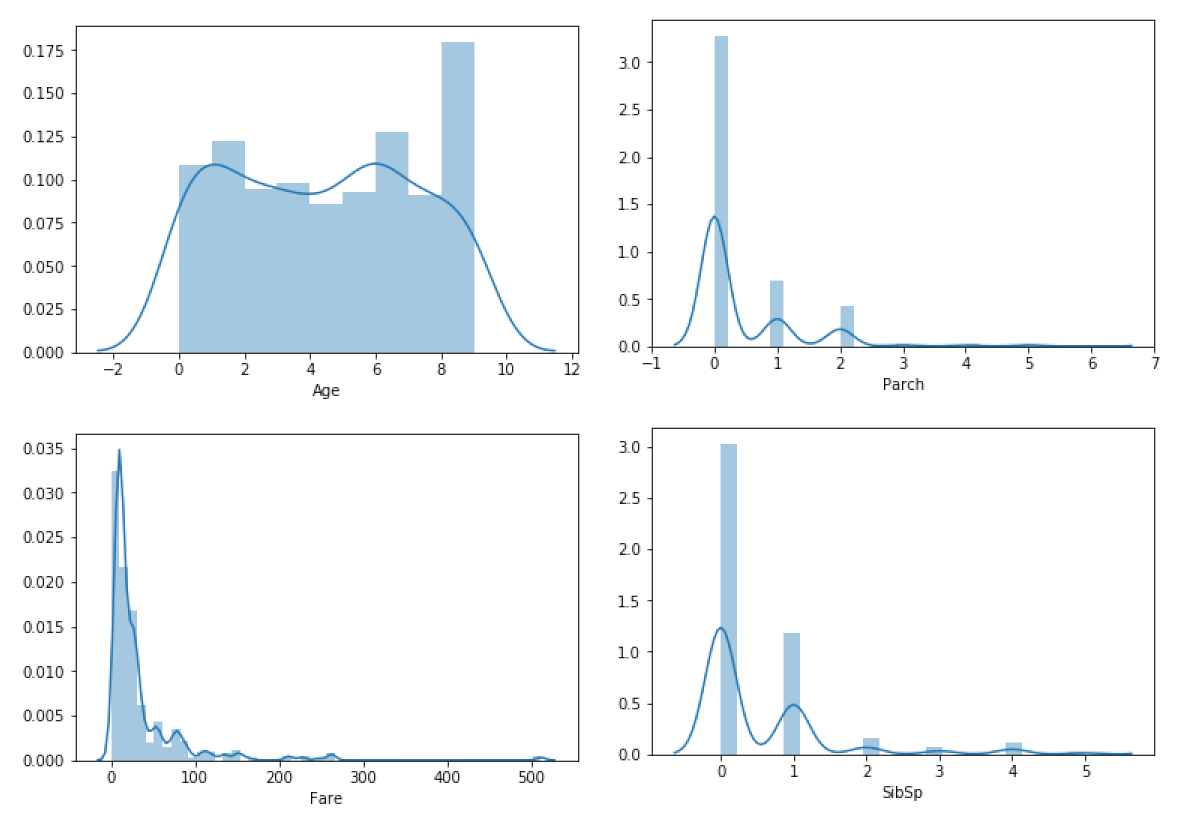

Глядя на непрерывные числовые признаки, можно увидеть, что распределение "Fare", "Parch" и "SibSp" близко к нормальному, но с асимметрией влево; распределение "Age" немного отлично от нормального, но это отклонение незначительно.

train.drop(['train', target, 'Pclass'], axis=1, inplace=True)
test.drop(['train', target, 'Pclass'], axis=1, inplace=True)

Разделим наши данные на тренировочные (80%) и валидационные (20%)

X_train, X_val, Y_train, Y_val = train_test_split(train, labels, test_size=0.2, random_state=1)

X_train.head()

Далее разделим тренировочные данные ещё на две части (в соотношении 70% на 30%)

Пошаговая реализация алгоритма БСД:

• Преобразование набора данных в частотную таблицу;

• Создание таблицы вероятностей, с нахождением этих вероятностей;

• Использование уравнения Байеса для расчета апостериорной вероятности для каждого класса, где класс с наибольшей апостериорной вероятностью является результатом предсказания.

В результате вся модель построена на вероятностях событий, которые и будут особенностями.

classifier = GaussianNB()

Обучим вторую часть данных. Обучение производится достаточно быстро.

classifier.fit(X_train2, Y_train2)
print('Metrics with only 30% of train data')
cross_validate(classifier, (X_train, Y_train), (X_val, Y_val))

Metrics with only 30% of train data
Model metrics
Accuracy  Train: 0.79, Validation: 0.76
Recall    Train: 0.75, Validation: 0.71
Precision Train: 0.71, Validation: 0.71

Обновим модель с первой частью тренировочных данных. Преимуществом БСД является возможность дообучения модели, причём до активации этого процесса модель можно наполнять новыми данными.

classifier.partial_fit(X_train1, Y_train1)

print('Metrics with the remaining 70% of train data')
cross_validate(classifier, (X_train, Y_train), (X_val, Y_val))

Metrics with the remaining 70% of train data
Model metrics
Accuracy  Train: 0.80, Validation: 0.76
Recall    Train: 0.78, Validation: 0.70
Precision Train: 0.69, Validation: 0.69

Как видите, метрические показатели модели улучшаются по мере того, как она обновляется оставшимися данными.

print('Probability of each class')
print('Survive = 0: %.2f' % classifier.class_prior_[0])
print('Survive = 1: %.2f' % classifier.class_prior_[1])

Probability of each class
Survive = 0: 0.60
Survive = 1: 0.40

print('Mean of each feature per class')
print('               Age         Embarked   Fare         Parch       Sex         SibSp')
print('Survive = 0: %s' % classifier.theta_[0])
print('Survive = 1: %s' % classifier.theta_[1])

Mean of each feature per class
               Age         Embarked   Fare         Parch       Sex         SibSp
Survive = 0: [ 4.5339233   1.23893805 22.97357316  0.37463127  0.86135693  0.5280236 ]
Survive = 1: [ 4.27391304  1.33478261 53.52155957  0.52608696  0.33043478  0.49130435]

print('Variance of each feature per class')
print('Survive = 0: %s' % classifier.sigma_[0])
print('Survive = 1: %s' % classifier.sigma_[1])

Variance of each feature per class
Survive = 0: [8.32554825e+00 2.88044224e-01 8.60096730e+02 8.36055467e-01
 1.19424042e-01 1.11647419e+00]
Survive = 1: [8.45106148e+00 2.74880003e-01 5.28959488e+03 6.75409304e-01
 2.21250514e-01 4.41231610e-01]

Проверим показатели модели с помощью тестовых данных

# К сожалению, наивный алгоритм Байеса sklearn в настоящее время не делает выводов, если какие-то данные упущены, поэтому необходимо заполнить все пропуски..
test.fillna(test.mean(), inplace=True)
test_predictions = classifier.predict(test)
submission = pd.DataFrame({'PassengerId': test_ids})
submission['Survived'] = test_predictions.astype('int')
submission.to_csv('submission.csv', index=False)
submission.head(10)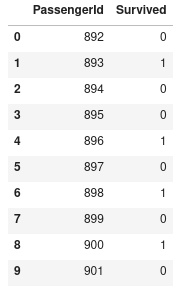

Плюсы и минусы БСД

Плюсы:

• Облегченное управление системами с ограниченной или противоречивой информацией. Людям несвойственно логически рассуждать о них.

• Легкое и быстрое предсказание новых данных. БСД также хорошо работает в прогнозировании мультиклассовых задач.

• Когда предположение о независимости выполняется, классификатор БСД работает лучше по сравнению с другими моделями (например, логистической регрессией), и требует меньше обучающих данных.

• БСД хорошо работает в случае категориальных входных переменных по сравнению с числовыми, так как для них предполагается нормальное распределение (колоколообразная кривая, что является сильным предположением).

Минусы:

• Методология проектирования. Не существует стандартного способа построения БСД.

• Если категориальная переменная имеет категорию (в тестовом наборе данных), которая не наблюдалась в обучающем наборе данных, то модель присвоит нулевую вероятность и не сможет сделать прогноз. Это часто называют «нулевой частотой». Чтобы решить эту проблему, мы можем использовать технику сглаживания. Один из простейших методов сглаживания называется оценкой Лапласа.

• БСД даёт вероятность, а не результат. По этой причине к выходным данным по вероятности, полученным с помощью predict_proba, не следует относиться слишком серьезно.

• Допущение независимых предикторов. В реальной жизни почти невозможно получить набор полностью независимых предикторов.

Проектирование БСД требует значительных усилий в сложных системах, и оно основано на знаниях экспертов, разработавших его. С другой стороны, эта черта может быть положительной, поскольку БСД могут быть легко проверены разработчиками и имеют гарантию, что используется информация, специфичная для предметной области.

Советы по улучшению возможностей байесовской модели:

• Если распределение непрерывных данных не нормальное, вы должны преобразовать эти данные.

• Если у набора тестовых данных проблема с нулевой частотой, примените методы сглаживания, или «преобразование Лапласа», чтобы предсказать класс набора тестовых данных.

• Удалите коррелированные функции, так как сильно коррелированные данные учитываются в модели дважды, и это может привести к завышению важности.

• Байесовские классификаторы имеют ограниченные возможности настройки параметров, такие как alpha=1 для сглаживания, fit_prior=[True|False] для изучения априорных вероятностей класса, а также некоторые другие параметры. Есть общие рекомендации по настройке этих параметров: одна из них — сосредоточиться на предварительной обработке данных и выборе способа распределения.

• Вы можете подумать о применении некоторых методов комбинирования классификаторов, таких как ансамбль, бэггинг и повышение, но эти методы не помогут, поскольку их цель — уменьшить дисперсию. У БСД нет дисперсии, которую нужно минимизировать.

Использованная литература

• Introduction to Bayesian Networks with Jhonatan de Souza Oliveira

• 6 Easy Steps to Learn Naive Bayes Algorithm with codes in Python and R

• Better Naive Bayes: 12 Tips To Get The Most From The Naive Bayes Algorithm

Всех желающих приглашаем принять участие в открытом уроке «Алгоритм Дейкстры для поиска кратчайшего пути во взвешенном графе». Регистрация доступна по ссылке.