
Астрологи объявили на хабре неделю профанных доказательств великих теорем.
- Теорема о четырёх красках.
- Теорема Ферма.
- Перед вами «доказательство гипотезы Римана».
Сначала я хотел тоже, оформить статью по приколу, что типа автор полностью уверен, что всё доказал, где мои деньги, но у меня, похоже, нет такого запаса самоиронии. Так что, обманываться вам придётся сознательно. А ещё, статья же для плюсов пишется, а не для минусов. Так что, вспоминаем о существовании юмора и продолжаем читать.
Итак, сначала по-быстрому (и не по-настоящему) докажем потрясающее очень хорошо сбалансированное равенство
С детского сада всем известно, что сумма геометрической прогрессии равна
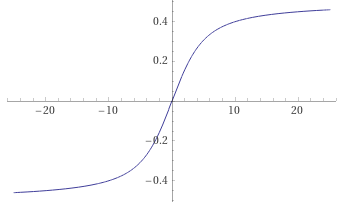
Значит
Если
Вот так забудешь поставить где надо различный знак и всё — сумма уже не нулевая, всё доказательство насмарку. Такое чувство, что при
Ладно, при нуле, может, и нет. Но при остальных значениях точно ноль. Поэтому даже верен интеграл
На этом, кстати, работает преобразование Фурье — интеграл имеет не нулевое значение только если частотная составляющая и колебательный множитель в показателе экспоненты под интегралом гасят друг друга в ноль.
Теперь надо вспомнить про дзета-функцию.
После замены переменных наша дзета-функция выглядит как приготовленная для разделки жареная курочка:
Ах да, надо ещё с тривиальными нулями что-то порешать. А то они внаглую идут только по чётным целым отрицательным числам, а у нас дробь
Но сам Риман сразу при открытии этой функции сказал: да [разве нужны нам]ер эти нули, вместе с полюсом. Берём, умножаем на всё что под руку попадётся.
Так что, составим соответствующее равенство, верное при таких нулях.
«Новые» нули функции именно это и обязаны делать. Конечно, если интеграл ноль, без разницы, что там за конечный множитель перед ним. Но и убирать этот множитель не надо, он должен помочь найти такое место, ведь прежде чем обнулиться функция должна потихонечку симметричненько уронить логарифм своего значения.
Смотря на это равенство, можно начать сомневаться, что и осевые нули бывают. Но нет — доказано, на оси нулей столько, что забирай — не закончатся. А вот то что не при любом
А ещё, может ли выполняться это равенство при не нулевых значениях интеграла? Мнимая часть точно должна быть нулевой, ведь она меняет знак. А реальная? Ну вот, даже прямое уравнение и то с подвохом. При нулевом
Будет, конечно прикол, если «новый» ноль окажется не на этой линии. Он, конечно, может быть на линии, но я же не проверял, что только на ней. У кси-функции линии нулевой реальной части и линии нулевой мнимой части чередуются, но ещё по оси идёт линия нулевой мнимой части. Так что, если пересечения линий не будет, новых нулей не ожидается.
Немного объясню прикол с нулевой суммой из начала статьи, а то может быть не понятно. Дело в том, что сумма всех натуральных степеней одного числа сходится только если число меньше единицы. Для комплексных чисел сравнение превращается из больше/меньше в направление изменения фазы — меня до сих пор удивляет, почему для математиков было открытием, что кроме вперёд/назад можно ходить и вправо/влево, и ещё разворачиваться в любом направлении. А больше/меньше определять можно отдельно для реальных или мнимых частей, или модуля. Для схождения модуль числа должен быть меньше единицы. Если число равно единице, то для суммы слагаемые аналогичны нулевой степени натурального основания, и сходиться такая сумма из бесконечности единиц точно не будет. А если модуль больше единицы, то тем более.
Если модуль равен единице, но фаза отличается, то сумма превращается в постоянное кружение вокруг одной точки, и вопрос спорный — эта точка как-то относится к тому, что должно получиться, или нет? А если добавить такое кружение с противоположной фазой, и значит, в другую сторону? Общее значение будет реальным и равным единице — за счёт того, что первый шаг — в котором фаза ещё не проявлена — дублируется. Но имеет ли такая сумма отношение к понятию суммы, и можно ли расширить нулевое значения сложения этих сумм для всех комплексных степеней? Условно, очень условно. Если говорить точно, то нет. Но если в аналитическом смысле, то совсем же другое дело.
Аналитика тоже может быть неожиданной. Например. Преобразование Фурье можно было бы считать суммой из двух различных преобразований Лапласа. Преобразование Лапласа — это интеграл, в котором множитель состоит из натурального основания в степени минус параметра — как преобразование Фурье, только без мнимого множителя, и с уменьшенным вдвое диапазоном интегрирования. Для комплексной функции колебания с одной частотой преобразование будет давать
Кроме того, ограничение на преобразование Лапласа определяют только одно из этих двух слагаемых — это максимум, другое при тех же параметрах не сходится. Так что, это тоже условно. Но условность интересная. Преобразование Фурье-то здесь равно дельта-функции не условно.
Второе слагаемое в особенной функции, конечно, подозрительное. С другой стороны, именно это слагаемое балансирует интеграл при определении нетривиальных нулей дзета-функции. И здесь, похоже, тоже балансирует.
Так что же за этим всем стоит? Если порассуждать: первое слагаемое понятное, второе слагаемое подозрительное, третье слагаемое не участвует в интеграле. И возникает по этому поводу такая мысль. А что, если существует и четвёртое слагаемое, только оно на столько странное, что даже не проявляется? Или, наоборот, всё доказательство сводится к тому, что такого слагаемого нет? Как доказать, что чего-то нет, если его нет? А, ну да, у нас тут гипотеза Римана, был бы наглядный пример.
Рассмотрим подробнее преобразование Фурье. Если задать функцию затухающего колебания
Если ограничить диапазон интегрирования, точнее, обнулить функцию для
Если сложить то что получится при изменение знака у
Эта статья ничем не заканчивается. Пойду чай попью.
Комментарии (20)

omxela
03.07.2022 21:38+1Другими словами, нечётная.
А почему она нечётная, наивно спрошу я. Если это прикол, то не смешной.

yurixi Автор
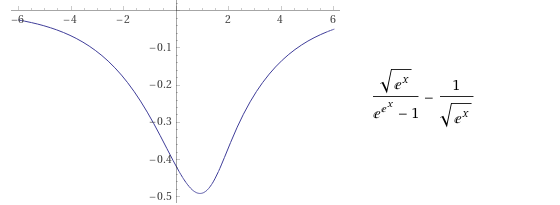
03.07.2022 22:51Конкретно тут ничего смешного — то что функция нечётная можно не только на графике посмотреть, но и проверить:
f(x)=-f(-x)
f(x)+f(-x)=0
1/(e^x-1)-1/x+1/2+1/(e^-x-1)-1/-x+1/2=1/(e^x-1)-e^x/(e^x-1)+1=(1-e^x)/(e^x-1)+1=-1+1=0
mayorovp
04.07.2022 01:25-1Кажется, доказывая что функция нечётная, вы только что воспользовались формулой (и доказали её!), для доказательства которой вам ранее была нужна нечётность функции...

Refridgerator
04.07.2022 10:17Автор вообще на корректности доказательств не заморачивается, о чём заранее честно и предупредил. А так
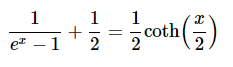 , нечётность котангенса известна по определению.
, нечётность котангенса известна по определению.

Pochemuk
03.07.2022 22:50+2… докажем потрясающее очень хорошо сбалансированное равенство… Для любого x.
Гы-ы-ы…Лемма 1. Крокодил более широкий, чем зеленый.
Доказательство: крокодил широкий как сверху, так и снизу, а зеленый только сверху.
Лемма 2. Крокодил более зеленый, чем длинный.
Доказательство: крокодил зеленый как в длину, так и в ширину, а длинный только в длину.
Опять же, из леммы 1 и леммы 2 следует: крокодил более широкий, чем длинный.

vics001
04.07.2022 00:41Почему все верят, что верна гипотеза Римана? Потому что если она верна, то верна знаменитая формула Римана про количество простых чисел, а она зависит от нулей на 1/2. Поэтому так как формулу уже очень хорошо посчитали никаких тривиальных нулей точно уже не найдут , только очень большие

Refridgerator
04.07.2022 08:43+2В самом начале пропущен интересный момент. Если построить график полученной геометрической прогрессии
спойлер, то хорошо видно, что в нуле она имеет разрыв, а по форме похожа на гиперболу. Если взять и вычесть из неё гиперболу — то эти разрывы взаимокомпенсируются, и особая точка в нуле получившейся функции становится устранимой. По-хорошему, доказательство этого и должно было быть далее приведено, потому что подобный фокус прокатывает далеко не во всех случаях.

yurixi Автор
04.07.2022 11:11В одной из предыдущих статей, Скучные числа, с этим обходится так: функция представляется как набор производных в нуле, по сути коэффициенты для ряда тейлора, и если от функции отнять значение в нуле, то можно поделить на x, все коэффициенты при этом сдвинутся в сторону уменьшения индекса, с делением на индекс своей позиции — вторую производную нужно будет поделить на два, третью на три. Это естественно для расскладывающихся в ряд тейлора функций.
Тогда с одной стороны, при таких шагах у функции с единицей в нуле добавится -1/x, который представляет собой разрывную функцию, с другой стороны, вместе с тем что останется, разрыв не появляется.
Для функции x/(e^x-1), содержащей в разложении числа бернулли, отнимаем 1, делим на x, прибавляем 1/2, получается нечётная функция, потому что все нечётные по индексу числа бернулли, кроме первого, равны нулю.

Hlad
04.07.2022 08:52+2Изначально у меня статья загрузилась вообще без формул. Получилось «если <пустое место>, то применяя формулу <пустое место> получаем <пустое место>, из чего следует вывод: <пустое место>» ну и так далее. Я прямо обрадовался, что такая концептуальная статья вышла на хабре. Но потом обновил страницу, увидел формулы, и даже расстроился…

Refridgerator
05.07.2022 06:18Если ограничить диапазон интегрирования, точнее, обнулить функцию для x>0,
точнее, умножить на функцию Хэвисайда (у вас в формуле) — то можно обнаружить, что значение функции Хэвисайда в нуле не определено (совпадение? не думаю).
yurixi Автор
05.07.2022 07:08Какое вы видите здесь совпадение? Для интеграла, думаю, точное значение в одной точке не так важно, особенно если оно в пределах [0;1]. При любом определённом значении результат был бы тот же.

Refridgerator
05.07.2022 07:30Ну что в нуле у вас всякое подозрительное происходит. А так, конечно, Лаплас через Фурье выражается вполне однозначно.


 , нечётность котангенса известна по определению.
, нечётность котангенса известна по определению.
Medeyko
Ну, “everybody knows, 1 + 1 + 1 + · · · = −1/2”! :)
yurixi Автор
Чтобы комментарий был доступен всем, я выделили и перевёл соответствующий фрагмент: