Многие удобные нам вещи — результат чьих-то расчётов. Благодаря людям, которые заняты этими расчётами, большинство может спокойно забыть о том, что многие важные аспекты нашей жизни зависят от чисел и их свойств. К старту нашего флагманского курса по Data Science напоминаем о математической красоте формата бумаги A4.
Если вы не из США и не прогуливали большую часть учёбы и работы, вы наверняка имели дело с форматом A4. Вы не задавались вопросом, почему формат этот имеет именно такой размер? Давайте смахнём пыль со школьного учебника по математике и разберёмся во всём.
Сообщу вам формат бумаги на случай, если вы его всё-таки не знаете. Это ровно 210 на 297 мм. Можете не верить мне на слово. Проверьте. Я подожду. Если у вас в доме не завалялось ни одного листа А4, вы гораздо тщательнее делаете уборку в доме, чем я… Мерить такой лист удобно обычной 30-сантиметровой линейкой, которая наверняка найдётся в ящике вашего стола или неподалёку от него. Теперь остаётся только один вопрос:
Почему?
И вслед за этим зачастую мы спрашиваем: «Вы это серьёзно? 297 миллиметров? А почему не 300?» Я знаю, что это искреннее недоумение. Эти слова до сих пор звучат у меня в ушах с того школьного урока черчения, на котором один из моих товарищей именно в такой форме сетовал об извращённости нашего мира. Не помню, получил ли он ответ, но боюсь, что его боль по этому поводу так никто и не разделил. Давайте потратим остаток статьи на утешение страданий этого мальчика.
Поможем прокачать ваши навыки или освоить самые востребованные IT-профессии:
- Полный курс по Data Science. Получите одну из самых перспективных профессий за 24 месяца.
- «Fullstack-разработчик на Python». Станьте незаменимым специалистом и универсалом за 15 месяцев.
- «Уверенный старт в IT». Пройдите лучший курс для новичков: попробуйте 9 профессий и освойте подходящую именно вам.
Воистину — каждый, кто когда-либо хотел отмерить половину листа бумаги, испытал лёгкое негодование. Немудрено: отмерить нужно 148,5 мм, а на линейке нет полумиллиметровых делений.
Предлагаю вам взять прямоугольный лист бумаги, отличный от листа формата А4. Ведь никто не мешает вам оторвать немного бумаги формата А4, а затем аккуратно сложить ее в прямоугольник. Взяв прямоугольник, отличный от А4, попробуйте сложить его ровно пополам [сверху вниз]. Вы увидите, что теперь лист бумаги вдвое меньше по размерам и совсем другой формы. Возможно, вы начали с «почти квадратного» прямоугольника, а теперь он стал «длинным и тонким», или наоборот.
Теперь проделайте это с листом A4. Кажется, вы уже поняли, что произойдёт. Вы получите формат A5. Он составляет половину формата А4 (ещё бы: вы же пополам складывали). Более того, форма осталась той же. Строго говоря, форма осталась аналогичной, соотношение сторон сохранено. Если вы хоть немного задумаетесь об этом, вы будете поражены. Ведь обычно прямоугольники так себя не ведут.
Возможно, эта «случайность» была одной из лучших идей XVIII века. Но пример приведу из наших дней: учителя уже много лет пользуются этим, чтобы буквально ополовинить свои затраты на ксерокопирование материалов. Хотите две копии на листе? Запросто — они отлично там уместятся! Но стоит взять любой другой формат (хотя бы, 8,5 х 11 дюймов, который североамериканцы величают «letter size») — и вы увидите, как куча бумаги уйдёт на совершенно ненужный зазор между двумя страницами.
Первая известная дискуссия по этой теме датируется 1786 годом — как и письмо от немецкого академика Георга Кристофа Лихтенберга его не менее известному соотечественнику Иоганну Бекману[1].
Однако есть предположения, что соответствующая задача давалась на экзаменах студентам задолго до этого[2].
Тем не менее только в ХХ веке Германия — а вслед за ней и большая часть мира — отразила эту идею в стандарте. Международный стандарт для формата бумаги получил номер ISO 216[3]
На самом деле существует лишь одно соотношение сторон прямоугольника, которое даёт аналогичную форму при складывании вдвое. Как вы думаете, какое? Нет, это не «золотое сечение», но тоже весьма интересное соотношение. Дальше я напишу, как его рассчитали.
Построим обычный прямоугольник с соотношением сторон (длинная к короткой) :
Теперь проведём линию половинного сгиба, чтобы получить прямоугольник с соотношением сторон (длинная к короткой) .
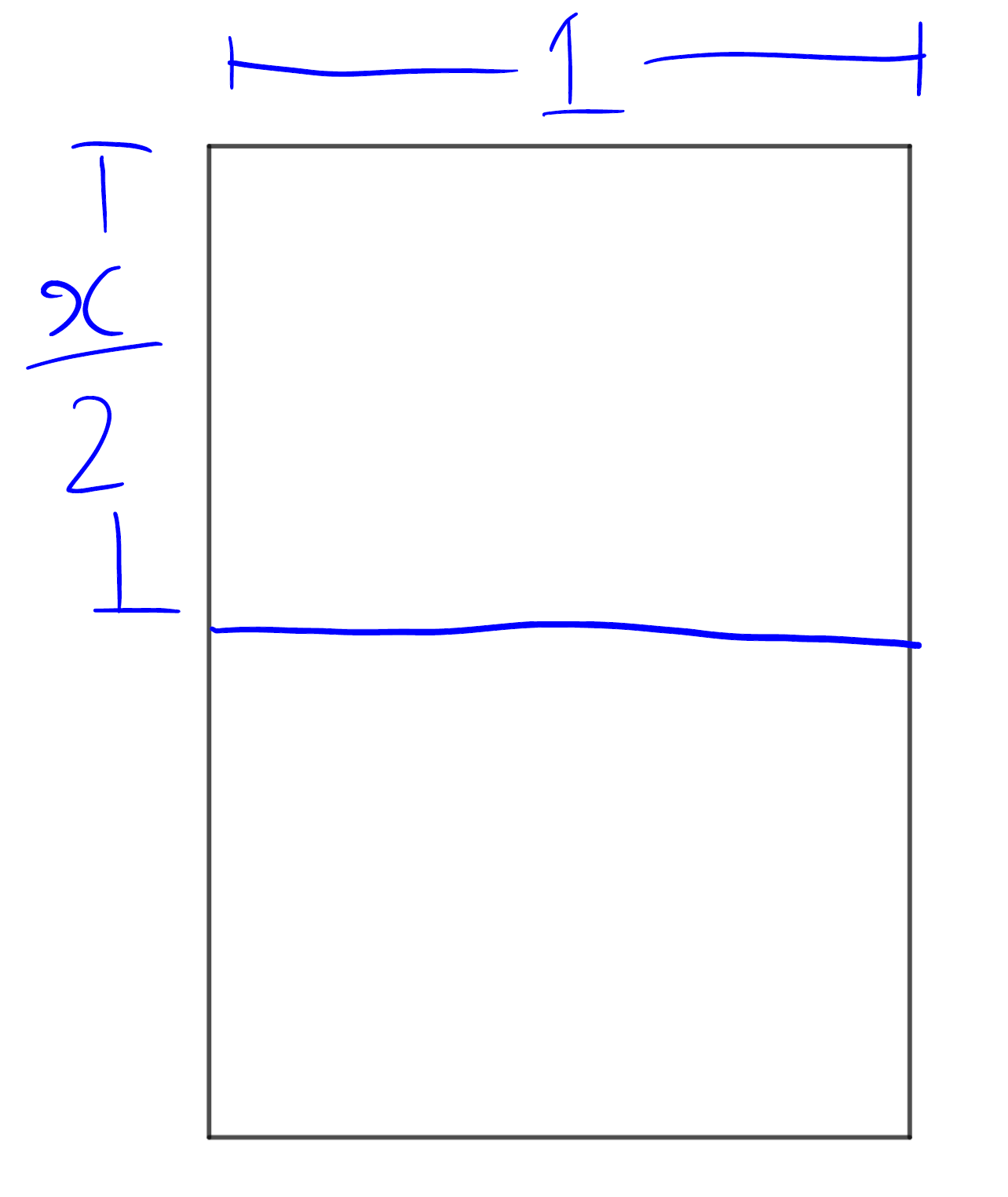
Если мы, во имя всех упомянутых благ, хотим, чтобы два соотношения были одинаковыми, мы должны получить равные дроби
(или , об отрицательных соотношениях поговорим в другой раз).
Этим важным свойством обладает только одно соотношение. Это квадратный корень из 2, который, как известно (а в данном случае — по иронии судьбы), дробью не является. Поэтому размеры бумаги, в каких бы величинах вы их ни измеряли, не будут целочисленными и, с точки зрения многих людей, «красивыми». Поскольку ни одна пара чисел не даст отношения , приходится прибегать к приближённым значениям.
Поэтому мы должны (и смогли) отказаться от мечты о «красивой» длине сторон, что не мешает нам получать «красивые» площади. На самом деле, современная международная система форматов «А» начинается с бумаги формата А0, со сторонами в правильном соотношении , но с площадью ровно 1 м2, или настолько близкой к ней, насколько это возможно при длине сторон в целых миллиметрах (1189 х 841 мм, если быть точным). Теперь складывайте этот лист вдвое и режьте его, пока он не уместится в папку и не станет удобным для работы. Вы получите формат A4, отсюда и «4» в названии.
Кстати, если вам всё это в новинку, но помнится кое-что из школьного курса математики, вам может понравиться другой способ понять это. Помните «коэффициенты масштаба площади» и «коэффициенты масштаба длины»? Коэффициент масштаба площади тождественно равен квадрату коэффициента масштаба длины. Так вот, если вы хотите, чтобы коэффициент масштаба площади был (или
), коэффициент масштаба длины должен быть
(или
). Конечно же, вы помните.
Нравится вам это или нет, но иррациональные числа полезны. Звучит отрезвляюще. А для некоторых — удручающе. Вспомним хотя бы миф о том, что сделали пифагорейцы с Гиппасом, который назвал выражение иррациональным). Но, как только мы преодолеем страх перед иррациональными величинами, мы сможем пожинать плоды. Теперь вес бумаги легко рассчитать, потому что он пропорционален площади: бумага плотностью 80 грамм на (квадратный) метр формата А0 весит ровно 80 г. Бумага формата А4 такой плотности весит 5 г, так как её сложили пополам 4 раза [уменьшили в 24, то есть в 16 раз].
Ширина стержня линера увеличивается на коэффициент . Таким образом, следующий линер в наборе подойдёт для следующего формата бумаги. Вот так красиво всё устроено.
Чертёжные ручки с маркировкой размера (с увеличением на коэффициент 1,4). Wikimedia Commons
Какой из этого можно сделать вывод? Многие удобные нам вещи — результат чьих-то расчётов. Благодаря им мы теперь можем спокойно забыть, что многие важные аспекты нашей жизни зависят от чисел и их свойств. Благодаря тому, что кто-то об этом не забыл.
Да, обо всем этом мы можем спокойно забыть. Но прошу вас: вспомните об этом, когда кто-то снова решит отмерить пол-листа, и вы снова услышите глас вопиющего в пустыне: "Ну почему 297?" Теперь вы знаете, что ответить.
[1] Тот самый Лихтенберг, который дал своё имя фигурам Лихтенберга, рисункам искровых разрядов высокого напряжения. И тот самый Бекман, который ввёл в науку термин «технология». Теперь вы это знаете.
[2] https://www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html.
Стать востребованным профессионалом в IT с самого начала или прокачаться помогут наши курсы. Скидка 45% по промокоду HABR:
Комментарии (72)

gchebanov
10.09.2022 02:15+1297−210√2≈0.015
Весьма неплохо, ошибка в 1/66 миллиметра.

Bender_Rodrigez
11.09.2022 02:321189-841√2 ≈0.3536
В больших форматах (которые, на минуточку, исходные) ошибка больше, математическая красота теряется, на мой взгляд.

v1000
10.09.2022 08:11+2Но стоит взять любой другой формат (хотя бы, 8,5 х 11 дюймов, который североамериканцы величают «letter size»)
Почему-то всё время был уверен, что пресловутое 210/297 это его метрическая версия. Поэтому не удивлялся такой странной размерности.

Iwanowsky
12.09.2022 01:02В советские времена, насколько я помню, наиболее популярная обычная писчая бумага (использовалась в т.ч. для печатных машинок, как правило, желтоватого оттенка) была немногим меньше размера А4, скорее всего как раз формата Letter (ANSI A, 8,5х11" или 216×280мм).

nimishin
10.09.2022 09:15+3Потрясающе, тоже задавался этим вопросом в школе и в институте, спасибо, отличный урок!

VladRepin73
10.09.2022 10:20-5По мне так Letter гораздо комфортнее. И писать на нём и читать с него. А4 как-той "цифровой". А Letter - тёплый, ламповый.

chnav
10.09.2022 10:48+6Даже без плашки "перевод", уже только по названию понятно, что статья рассчитана на иностранного читателя. Очень странно, что очевидные со школы факты удивили кого-то на Хабре.
Мне как-то ютуб подкинул ролик, в котором иностранец сравнивает английскую и метрическую системы мер и на полном серьёзе рассказывает всю прелесть метрики, демонстрируя что в одном метре 1000 миллиметров, а в одном километре 1000 метров...
freecoder_xx
10.09.2022 11:05+30Мне о форматах A в школе не рассказывали. И моим знакомым - тоже.

AlchemistDark
12.09.2022 09:04А в какие годы это было? Просто это рассказывали на уроках черчения (школьная версия начертательной геометрии), которые из школьной программы убрали в 00-е.

freecoder_xx
12.09.2022 18:38У меня было черчение. Более того, я занимал первое место в городской школьной олимпиаде по черчению.

13werwolf13
10.09.2022 12:35+15я много лет назад, в школе, задал вопрос почему размеры старон у листа A4 именно такие.. ответ узнал вот только что.
очевидные для одних школьные факты другим в других школах не преподаются, я учился в школе с такими учителями что слава богу что хотя бы 2+2=4 меня не удивляет..

nikolas78
10.09.2022 16:34+1Вот если бы в школе больше преподавали вот таких простых и одновременно интересных вещей, то насколько бы больше было желающих учиться лучше!

13werwolf13
10.09.2022 16:48+1Полностью согласен
Я учился в двух школах, колледже и умирающем вузе. За это время я встретил только одного преподавателя с большой буквы, он и знал свой предмет, и умел донести, и что очень важно умел заинтересовать. Его слушали даже гопники с "комчатки", и один из таких рас3.14здяев сейчас неплохо зарабатывает занимаясь тем что преподавал этот препод. Остальные же зачастую свой предмет особо и не знали, верх фиерии была преподша по базам данных которая пыталась нас учить mysql по книжке mssql и была удивлена отсутствию гуя и sa/sa уже на первой же лабороторной.
Но справедливости ради преподавать сложно, а перегореть на такой работе просто..

Willy64
10.09.2022 14:34+4Аналогично открываются глаза при переходе с МОА (minute of angle) на миллирадианы в определении расстояния с использованием меток оптического прицела. Расчеты, оказываются, могут быть несложными, без дюймов и ярдов, без длинных дробей!

Daddy_Cool
10.09.2022 12:42+1Читал про это давно, но... подзабыл ) А что площадь A0 равна 1 кв. метру - не знал.

kambala
10.09.2022 12:57+2есть полностью «наша» статья, которая, как мне кажется, на порядок лучше: https://book.etudes.ru/articles/a4/

Mingun
10.09.2022 13:27Статья действительно хорошая, правда, я там так и не увидел, что это за серия форматов «C» (хотя она там и упоминается). Логически я могу предположить, что у этой серии длина большей стороны равна 1 м (в противоположность серии «B», где одному метру равна длина меньшей стороны), но хочется всё же «железобетонного» подтверждения :).

ZyXI
10.09.2022 19:38+2В wikipedia всё есть. И это, оказывается, конверты для серии A. Правда, в английском варианте написано немного не так: Cx это геометрическое среднее между Bx и Ax, в основном используемое для конвертов.

baldr
10.09.2022 13:46+1Есть статья в википедии, которая объясняет все то же самое, вдобавок про форматы B и C тоже пишет.
Однако, за статью спасибо, привлекла внимание к этим интересным фактам.

Didimus
10.09.2022 19:52Если формат letter такой нерациональный, почему в Америке им пользуются?

Timoffey
10.09.2022 20:03+9А зачем они фунтами и футами и дюймами и галлонами пользуются, которые вообще слабоконвертируемы между собой? И фаренгейтами?

Otard
11.09.2022 13:36Фаренгейты в поседневной жизне могут быть удобнее цельсия.
А в американском строительстве дюймы и футы гораздо удобнее метричесой системы.

Samid777
10.09.2022 21:40И не только листиками такими пользуются, но и системой мер. Если уже чтото одно приняли, и все этим пользуются, то поменять потом на более удобное не так быстро и просто, перейти на метрическую систему так же не удобно, как и нам будет перейти на любую альтернативную.

romancelover
10.09.2022 20:51+4Формулу расчёта так и не написали (почему именно 297 мм). Если соотношение сторон листа A0 равно sqrt(2), а площадь 1, значит его длинная сторона равна sqrt(sqrt(2)). Каждый следующий лист в серии меньше в sqrt(2) раз, значит, А4 меньше в 4 раза ( pow(sqrt(2),4) ). Длина стороны листа А4 в метрах равна корню четвёртой степени из двух, делённому на 4, или 0,297301778751 м. Округление до 1 мм даёт 297 мм.

Samid777
10.09.2022 21:38+1Однажды вдруг задумался, какое соотношение может обеспечить возможность делить лист на 2 части так, чтобы соотношение сторон не менялось. Сразу догадался что это корень из двух, правда математически не понял почему. Тут же проверил. Так и оказалось. А вот про деленный квадратный метр я долго не знал. Все хорошо продумано.

BubaVV
11.09.2022 12:54Еще слышал формулировку "11 формат" про А4

qyix7z
12.09.2022 14:18В вики все написано
Чертёжные форматы в СССР в 1960-1968 гг.В советской чертёжной терминологии[1] по ГОСТ 3450-60 (то есть 1960-го года) формат А4 являлся исходным для всех остальных и назывался «формат 11», Форматы обозначались двумя цифрами, первая из которых указывает кратность одной стороны формата размеру 297 мм, а вторая — кратность другой стороны формата размеру 210 мм. Формату А3 соответствует формат 12, А2 — 22, А1 — 24. Произведение двух цифр в обозначении формата определяет количество форматов 11, которое содержится в данном формате. Например, формат 44 с размерами сторон листа 1189×841 мм содержит 4×4, то есть 16 форматов 11. Кроме этого, таким образом обозначены форматы бумаги, отсутствующие в серии А, например, формат 14 для чертежей длинных объектов. По ГОСТ 2.301-68 обозначение форматов для чертежей принято в соответствии с ISO 216.

ViktorZ
12.09.2022 12:10Удивительно, но я только пару дней назад закончил перевод этой статьи. Перевод вольный, я убрал часть текста, так как посчитал это водой. И я даже изменил название, так как, мне кажется, "Красота математики в формате бумаги A4" звучит коряво. Я не придумал ничего лучше, кроме как назвать статью "Почему бумага формата А4 имеет размер 297 мм на 210 мм?".

vinodimus
12.09.2022 16:54Странно, что в Советском Союзе не было формата A4, хотя после революции Россия перешла на метрическую систему. Вспомните писчую бумагу для печатных машин или листы ватмана для черчения или альбомы для рисования. Там длинная сторона была длиннее чем в A4






nickolaym
Не раскрыта тема "ну почему 210?!!! почему не 200?"
А вообще, такое количество воды налили, что возникает вопрос-продолжение: а в ваших курсах, которые рекламируете, тоже так же разливанно?
sbw
Потому что берём меньшую сторону формата А0 и делим её на 4:
841/4=210.25 ≈ 210
Bender_Rodrigez
Почему 841?
geher
Потому, что А0 - это 1 квадратный метр ровно. При нужном соотношении сторон красивые длины в миллиметрах не вытанцовываются.
Следующий очевидный вопрос: почему в основу стандарта положили красивую площадь, а не красивую длину одной стороны? Вот на него хотелось бы таки получить ответ.
Есть, правда, предположение, что это упрощает оценку стоимости бумаги, которая идет за количество квадратных метров. Но как оно было на самом деле?
domix32
да не ровно же, а приблизительно равно. Ну не делит корень из двух метр ровно.
geher
Так "ровно" же в этом случае даже на уровне длины стороны в целых миллиметрах - плюс-минус небольшой лапоть. Потому этой погрешностью можно пренебречь.
Может быть и так, но это только гипотезы. Интересно мнение именно авторов стандарта, если оно вообще сохранилось в истории.
И где эта серия В? :Живьем она встречается, мягко говоря, существенно реже, чем А.
Хотя, опять же, в порядке гипотезы, могли предложить два варианта стандарта сразу (играющий от площади и играющий от длины стороны), а потом посмотреть, какой "взлетит".
В школьной программе этого вроде никогда не было. В мое время это знание доводили только до тех, кто на УПК попал на техчерчение. От попавших туда я и узнал. Даже не в каждом вузе это до студентов доводят. Только там, где чертежи на бумаге рисуют, да и то не везде.
geher
И, кстати, еще момент. Конверты под серию А (стандарты серии С) предусмотрены. А под серию В?
Moskus
Утверждается, что первый раз размеры бумаги ряда А были предложены во время Французской революции, а самый большой из описанных соответствовал формату А2 (четверть квадратного метра по площади). Размер мог быть выбран из каких угодно соображений, включая "красивую" площадь, учитывая, что метрическая система только (буквально в те же годы, чуть раньше) начала внедряться.
Solozhenitsyn
В 1798 году был принят закон о гербовом сборе в зависимости от площади листа бумаги, соответственно и размеры выбирали исходя из простоты финансовых расчетов. Вот текст закона: https://legilux.public.lu/eli/etat/leg/loi/1798/11/03/n1/jo
Radisto
В школьной программе вероятно не было, но мне учительница в школе это сказала. Наверное по собственной инициативе
AlchemistDark
У нас в школе это было совершенно точно. Правда я не в самой обычной школе учился.
hollycon
В свое время попался мне учебник черчения для 7 класса, в нём все эти знания были втиснуты в первый урок. Хороший учебник, простое его чтение позволило понимать требования инженерной графики в институте.
Учебник был начала 80-х. В конце пресловутых 80-х черчения уже небыло.
HiTechSpoon
Может быть так проще было посчитать количество листов в большой пачке - просто взвесив её? Ведь плотность бумаги измеряется в г/м^2, отсюда удобнее посчитать вес, если размер бумаги будет кратен квадратному метру. Например, 1 лист A0 плотностью 80 г/м^2 весит примерно 80 г, тогда 1 лист A3 будет весить
0.125 * 80 = 10 г.Moskus
Вы уверены, что во времена Французской революции плотность была та же?
HiTechSpoon
Плотность бумаги вы имеете в виду? Так она и сейчас разная есть. Я неверно выразился. Я предположил, что используя квадратный метр проще считать и вес бумаги из плотности, и её плотность из веса.
sanalex76
Вес еще и от влажности зависит. И довольно сильно - бумага очень гигроскопична.
Bender_Rodrigez
Какой толщины?
Solozhenitsyn
Длина стороны лежит в основе форматов серии B. B0 имеет ширину 1 метр: https://ru.wikipedia.org/wiki/ISO_216#/media/Файл:B_size_illustration2.svg
ShaVas
В статье же про это написано: потому что 841мм * sqrt(2) = 1189мм (длинная сторона). А 841мм*1189мм ≈ 1000000 мм кв. = 1 м кв.
select26
Статью прочтите целиком.
В ней именно об этом говорится.
Bender_Rodrigez
Я прочитал, и там говорится о некоторых хардкодед-значениях типа 841, 297, 1 м2, 80 г/м2.
Но вы хотите сказать, что лист плотного картона формата A0 и калька формата А0 весят одинаково?
В статье и комментариях многие аргументы красоты чисел основываются именно на этих значениях, игнорируя, например, тот факт, что существует бумага другой плотности: https://abc-paper.ru/weight-sheet/
Например, 1 лист A3 плотностью 110г/м2 будет весить
0.125 * 110 = 13,75 гТаким образом, под площадь в 1м2 подгоняют толщину, а о ней ни слова. И при всей красоте 1 м2 вся суть в этом.
Банальная манипуляция баландой из воды с цифрами.
Scootaloo
Да господи. Не вес, ПЛОЩАДЬ. Всë пошло от площади А0 = 1 метр квадратный, потому что так удобнее считать. Так как надо было получить уменьшенные форматы такого же соотношения - пришли к корню из двух. Сложили корень из двух и нужную площадь - получили длины и всю систему форматов.
Bender_Rodrigez
Вы прочитали комментарий полностью и поняли смысл сказанного? Обратного в нем не говорится, позволю заметить, ваш краткий пересказ статьи, как и сама статья, не даёт ответа на второстепенные вопросы, связанные с красотой чисел формата на основе константной площади. Прочитайте ещё раз заголовок статьи.
Суть в том, что все величины пытаются увязать в одно, в данном случае, исходя из того, что исходный формат А0 имеет фиксированную площадь и какбэ из-за этого получается, что и вес считается в целых цислах для удобства. Но, только для плотности 80 г/м2, т.е. для вполне определённо подобранной толщины листа, которая не регулируется и исключена из рассмотрения (почему именно такая?). Для другой плотности расчёты не столь удобны.
Так вот, в продолжении темы - Почему 1 м2 - это удобно, а целое значение одной из сторон листа - нет?
Формат В0 имеет размеры 1000х1414, В1 707х1000 - тот же корень из 2. Удобно? Да. Но общепринятым стандартом считается А0. И толщину листа тоже можно подобрать таким образом, чтобы в дефолтной плотности расчёты веса были удобны.
Всё зависит от того, какую величину вы зафиксируете в качестве стандартной - площадь, длину или вес.
inkelyad
Я подозреваю, что линейка B не стала популярной просто потому, что B4 слишком большой и в существующие пишущие машинки не всегда влазил, а B5 - уже слишком маленький.
AlchemistDark
297/√2≈210
Bender_Rodrigez
Да, а 1189/√2≈841, но вопрос в другом.
AlchemistDark
Если вас интересует плотность бумаги, то это не тоже самое, что плотность материала в физике. Конечно, она зависит от толщины, только обычно у бумаги определённой плотности всегда одна и таже толщина. Они намертво связаны стандартами. Это видно если сравнить обозначение плотности бумаги и обозначение плотности других материалов.
А статья не об этом.
AVPro
потому что площадь = 1м2, а соотношение сторон единица и корень из двух
imater
Когда меня раздражает всё что требует подумать или длиннее 15 минут или надо долго задумываться – я делаю вывод, что мой потолок – Тикток
Format-X22
Это хорошо, меньше конкуренции для думающих.
Erop22
Для думающих меньше конкуренции — плохо.
Format-X22
Это был сарказм, хотя в чём-то и не совсем.
HiTechSpoon
Видимо, потому что для стороны 200 исходный формат А0 должен быть 800x800√2 т.е. 800x1131.371 - не удобная для измерения цифра.