
Мир криптографии постепенно готовится к приходу квантовых вычислений, где вместо двоичной логики используются кубиты. Предполагается, что именно криптография станет одним из первых применений квантовых компьютеров.
Проблема в том, что современные алгоритмы вроде RSA и Диффи-Хеллмана (в том числе на эллиптических кривых) не способны противостоять квантовым атакам. Поэтому в июле 2022 года Национальный институт стандартов и технологий США (NIST) опубликовал набор алгоритмов шифрования, потенциально способных противостоять взлому на квантовых компьютерах — так называемые «постквантовые шифры».
Один из «постквантовых» шифров сразу взломали. Но самое интересное — метод, который применили исследователи.
Алгоритм SIKE
В июле 2022 года после многоступенчатого отбора NIST определил оптимальный универсальный алгоритм CRYSTALS-Kyber и ещё четыре алгоритма общего назначения BIKE, Classic McEliece, HQC и SIKE, которые требуют доработки.
NIST предложил исследователям проверить опубликованные алгоритмы на наличие уязвимостей с вознаграждением $50 тыс. за удачный взлом.
Алгоритм SIKE базируется на суперсингулярной изогении, то есть кружении в суперсингулярном изогенном графе. Основу SIKE составляет протокол под названием SIDH (Supersingular Isogeny Diffie-Hellman).
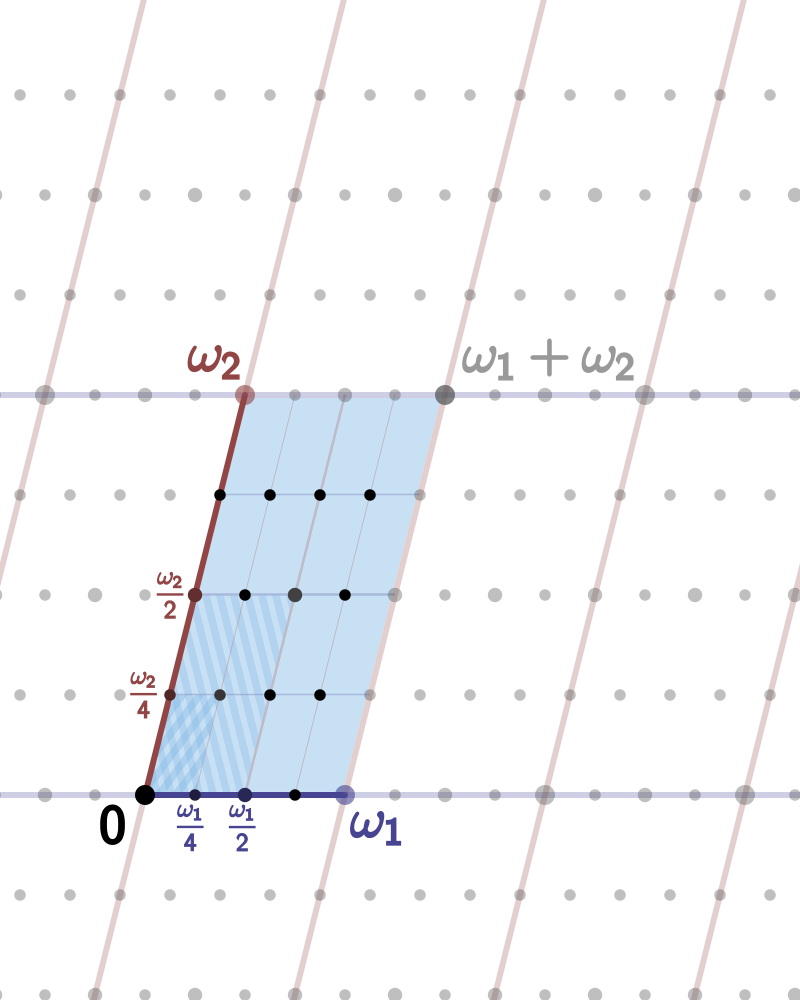
Изогенные эллиптические кривые к многообразию E можно получить факторизцией E по конечным подгруппам, которые представлены как подгруппы 4-кручения, источник
Исследователи из Католического университета в Лёвене (Бельгия) довольно быстро взломали алгоритм SIKE, за что получили заслуженную награду (об этом упоминали на Хабре в августе 2022 года).
Для нахождения секретного ключа понадобилось задействовать всего одно ядро старенького процессора Xeon E5-2630v2 на тактовой частоте 2,60 ГГц. Вычисление заняло менее часа.
Но более интересны подробности этого взлома, которые можно почитать в кратком комментарии профессора математики Стивена Гэлбрейта, пресс-релизе Королевского университета Канады и научной статье самих криптографов Воутера Кастрика (Wouter Castryck) и Томаса Декру (Thomas Decru).
Теорема 1997 года
Уязвимым местом шифра SIKE оказалась математическая теорема, вероятно, не знакомая авторам шифра и составителям конкурса NIST. Это научная статья д-ра Эрнста Кани от 1997 года. Данная теорема связана с абстрактным манипулированием математическими объектами для исследования их различных свойств.
В теореме Кани обсуждается процесс «склеивания» двух эллиптических кривых — и при каких условиях эта процедура может дать сбой. Собственно, один из описанных в статье вариантов сбоя использовался в реализации SIKE, что дало естественный путь к взлому этого алгоритма с помощью «адаптивной атаки GPST», описанной в статье «О безопасности криптосистем с суперсингулярной изогенией» (2016), которая разработана на основе вышеупомянутой работы 1997 года.
В августе 2022 года соавтор статьи о GPST профессор Гэлбрейт пояснил: ключевая уязвимость SIKE состоит в том, что SIDH вычисляет изогению не напрямую, а через вспомогательные точки, причём степень изогении известна. Таким образом, для атаки можно применять готовый математический аппарат, разработанный в 1997 году.
Как и GPST, атака на SIKE просто определяет промежуточные кривые
«Один из соавторов алгоритма SIKE выразил удивление по поводу того, что кривые второго порядка можно использовать для получения информации об эллиптических кривых. Но именно такой была наша первоначальная стратегия в 1980-х и 1990-х годах (и после)», — сказал доктор Кани в комментарии для пресс-службы университета.
Успешный взлом SIKE доказывает, что он не может быть надёжным средством шифрования, сужая поле возможных кандидатов для технологий постквантового шифрования. Эта история ещё раз демонстрирует силу и мощь глобального научного сообщества, которое действует как единое целое и движет вперёд технический прогресс с неизбежным постоянством.
Важность теоретической науки
Математическая теорема Кани 1997 года — чисто теоретическая работа, при написании которой автор вряд ли предвидел возможные практические применения. В этом нет ничего удивительного. И сейчас учёные в области теоретической, фундаментальной физики и математики не могут представить, для каких реальных приборов будут использоваться их формулы через 100, 1000 или 10 000 лет.
Например, французский математик Пьер Ферма в 1637 году во время факторизации больших чисел сформулировал некоторую любопытную теорему. И только в 1978 было найдено её применение в криптографии.
Все методы шифрования данных — это математика. Поэтому и новейшие системы постквантового шифрования тоже основаны на научных достижениях прошлых веков.
Управляемая инфраструктура PKI GlobalSign – это защищенная SaaS-платформа, которая позволит вам полностью контролировать работу с сертификатами на базе единой централизованной учетной записи. API-интерфейсы, интеграция с Active Directory и инструменты учета упростят автоматизацию и отслеживание развертываемых сертификатов.
Более подробную информацию вы можете найти на нашем сайте: www.globalsign.com/ru-ru/managed-pki

Комментарии (43)

izogfif
29.01.2023 18:04+22Прям напомнило случай, произошедщий с ребятами из нашего класса на городской олимпиаде по математике. По средам мы (несколько человек из нашего и параллельных классов той же школы) оставались в школе после уроков и ходили на кружок математики, где решали и разбирали интересные задачи олимпиадного уровня. Иногда его вел сам автор учебника, по которому мы занимались, а иногда наша учительница по математике.
И вот мы собрались, порешали несколько задач с нашей учительницей, пару по геометрии посмотрели, разобрали доказательство одной теоремы (названной в честь какого-то математика N-ского) про соотношение частей сторон треугольника, в который как-то по-хитрому вписана окружность, ну и собственно формулу соотношений. Все все поняли, и разошлись по домам.
А назавтра, в четверг, была олимпиада. И на ней самая-самая сложная задача с наибольшим количеством баллов была та, в которой нужно было рассчитать отношение частей сторон. В треугольнике. В который вписана окружность. Ровно так, как вчера разбирали. Ну, я ничтоже сумняшеся, написал: "По теореме N-ского соотношение будет вот таким". И выписал ту самую формулу из головы. Это было все, что я написал в решении к этой задаче. Мне за нее дали только половину баллов.
Мой одноклассник написал то же самое, но в качестве пояснения еще привел и доказательство той самой теоремы, которую разбирали вчера. Ему дали полные баллы.
Потом наша учительница, у которой, по-видимому, были знакомые в жюри: какой-то преподаватель из жюри, собственно и придумал эту самую задачу. Он вывел соотношение каким-то хитрым способом, гораздо более сложным, чем тот, что описан в теореме N-ского. И, по своему опыту убедившись в том, что она ну очень сложная, добился того, что ее включили в состав олимпиадных задач и присудили наибольшее число баллов.
То, что описано в данной статье, очень напоминает тот случай: придумали сложную конструкцию, не изучив недостатки частей, притом, что сами части и их недостатки давно уже задокументированы. А как на них указали, то вместо:
Ой, сорри, нужно было лучше документацию изучать.
написали:
Эта история ещё раз демонстрирует силу и мощь глобального научного сообщества, которое действует как единое целое и движет вперёд технический прогресс с неизбежным постоянством.
Прям так и вижу: двоечник стоит у доски, учительница спрашивает у класса "кто-нибудь заметил ошибку?" Весь класс поднимает руки и указывает на ошибку. И тут учительница вместо "садись, два; дома учить надо было" закатывает: "это демонстрирует силу и мощь..."

thevlad
29.01.2023 18:27+29Современная математика, огромна и узко специализирована. Всегда есть шанс, что обнаружится какая-то магия связывающая что-то из кажущихся на первый взгляд не взаимосвязанных областей.

Mingun
29.01.2023 20:19+3Да что там олимпиада, в части 3 на ЕГЭ по математике была задача, элементарно решаемая по теореме, которой в школьной программе не было, однако, её доказательство было одной из задач со звёздочкой, предлагаемых в задачах ЗФТШ при МФТИ за 11 класс, где я учился. К сожалению, не помню название теоремы, но связывала она стороны двух хитро построенных треугольников с общей стороной и углом. Без этой теоремы на ЕГЭ пришлось бы попотеть, отвечая на заданный вопрос, а при использовании теоремы ответ элементарно вычислялся по формуле соотношения сторон.

Arqwer
30.01.2023 15:45+1Теорема Минилая?

izogfif
30.01.2023 16:30Ух ты, так это ж она вроде как и есть. Я про окружность ошибся, зря про нее в комментарии написал. Но дело было давно, так что шансы вспомнить были крайне малы.

Mingun
30.01.2023 17:17Точно, вроде как она. Хотя, помнится, в задачнике ЗФТШ её условие по-другому звучало, что-то не помню в нём ничего про произведение отношений направленных отрезков, равное минус единице (хотя, может, и ошибаюсь, дело давно было). А ещё моё доказательство было значительно обширнее того, что приведено по ссылке в Википедии.

GospodinKolhoznik
30.01.2023 10:20+6Если учительница вместо "это демонстрирует силу и мощь..." говорит "садись, два; дома учить надо было", то ей самой самое место вахтершей работать, а не учительницей. Их в пед ВУЗе 5 лет учат тому, как замотивировать детей на изучение предмета, как добиться того, чтобы дети делали домашка не из страха получить двойку, а из интереса узнать что то новое. И все, на что она способна после 5 лет обучения это "садись два"? Абсолютная непрофпригодность, вон из профессии!

Manwe_SandS
31.01.2023 08:50+1Да, аналогия с учительницей без эмпатии не очень удачная. Но и пафос про «единое целое», шагающее в ногу и связанное одной цепью-целью – нонсенс.

Manwe_SandS
31.01.2023 08:47Да, меня тоже покоробила фраза «действует как единое целое». Наоборот, благодаря тому, что каждый действует независимо, и удаётся находить новые решения, исправлять старые ошибки и тому подобное.

pda0
29.01.2023 18:16+24Вот будет весело, если в итоге окажется, что шифр может быть стойким либо классически либо квантово...

p07a1330
29.01.2023 20:50+9Не может быть такого
Потому что есть шифры с теоретической абсолютной криптографической стойкостью.
Ярчайший пример - шифр Вернама (aka шифр одноразового блокнота)
Простой как дверь, но его нельзя сломать. В принципе
georgevp
29.01.2023 21:08Математически - да, однако, нематематически ...

Wesha
29.01.2023 22:54+9

Arqwer
30.01.2023 18:15+1Комикс этот уже поднадоел. По сути это шутеечка, и не более того. Есть масса приложений криптографии, где в голове не хранится ключ от явно зашифрованных данных. Гаечный ключ никак не поможет взломать TLS соединение. Не поможет деанонимизировать пользователей TOR и I2P. Не поможет списать деньги с multisig кошелька группы из нескольких человек, находящихся в разных странах. Не говоря уже про прямые средства противодействия гаечным ключам, такие как стеганография, облака, удалённый отзыв прав доступа, итд. Слышал, что в АНБ учат смело сообщать все пароли и ключи в случае пыток, потому что при поимке АНБшника все его доступы сразу аннулируются. А этот комикс, вместо того, чтобы научить чему-то хорошему, выставляет ситуацию так, будто бы единственный разумный выбор - это сложить лапки и капитулировать.

DmitryKoterov
29.01.2023 21:13+3В нем разве длина ключа - это O(1) от длины потенциального сообщения?

Boilerplate
29.01.2023 21:23+6Абсолютно стойкий шифр подразумевает ключ сравнимый с информацией. И тогда встает вопрос о безопасной передаче такого ключа. Понятно, что никакие вычислительные мощности не сломают банальный XOR с одноразовым блокнотом.

HappyGroundhog
29.01.2023 23:27На одном из CTF была именно такая задача. Всё никак не доберусь статью про неё написать) Но в конкретных случаях задача очень даже решаема...

alhimik45
30.01.2023 00:42+2Решалась как в Криптономиконе?)

HappyGroundhog
30.01.2023 09:10Было бы красиво) Но банальная атака по известному открытому тексту, а дальше использование этого знания.

Komrus
30.01.2023 11:13+1А как поможет атака по известному тексту против ОДНОРАЗОВЫХ шифроблокнотов?

HappyGroundhog
30.01.2023 11:20Это CTF. Там не нужно ломать все сообщения, достаточно сломать только одно.
В теории такое шифрование неуязвимо. На практике могут дважды использовать один блокнот/плохо вынимать шары и т.д. CTF на то и CTF, чтобы иметь неочевидное решение вроде бы нерешаемой задачи

p07a1330
30.01.2023 19:47+1На практике могут дважды использовать один блокнот
Тогда это не шифр одноразового блокнота
В том и фишка

thevlad
29.01.2023 21:28+1А есть такие с доказанной теоретической стойкостью для ассиметричной крипты? Потому что к примеру даже для факторизации чисел не доказано, что это np-complete задача.

lrrr11
30.01.2023 08:28нет. Больше того, не доказано даже, есть ли в принципе такие задачи.

thevlad
30.01.2023 11:27Поискал для интереса, нашел к примеру https://en.wikipedia.org/wiki/Multivariate_cryptography там утверждается, что задача лежащая в основе NP-complete.

lrrr11
30.01.2023 11:32верно. Но никто не доказал, что P != NP. Вот статья по теме. Например все думали, что дискретное логарифмирование является такой функцией. Но потом оказалось, что при наличии квантового компьютера таки нет - что и послужило причиной появления всех этих SIKE и т.п.

thevlad
30.01.2023 11:46Квантовые компьютеры это отдельная тема, хотя бы гарантии для классических. Ссылаться на P != NP с практической точки зрения не серьезно.

lrrr11
30.01.2023 12:56А есть такие с доказанной теоретической стойкостью для ассиметричной крипты?
Ссылаться на P != NP с практической точки зрения не серьезно
раз вы такой серьезный, то для начала определитесь, какая точка зрения нужна, теоретическая или практическая. И кстати, даже с практической точки зрения NP-полнота задачи не гарантирует отсутствие успешных атак на алгоритм на ее основе.

thevlad
30.01.2023 13:04Не дает, но это хотя бы какие-то относительно твердые гарантии. P not NP не доказана, но все разумные люди понимают, что эта гипотеза верна. Возможно еще пройдет несколько столетий прежде чем она будет доказана, как было с Великой Теоремой Ферма.

pda0
30.01.2023 11:43Даже если ограничить шифрованием с открытым ключом, всё равно веселья полная охапка останется.

vassabi
29.01.2023 21:09это еще не самое страшное,
бывало так что предлагали использовать шифры, которые специально ослабляли\вставляли бекдор.

AlexeyK77
30.01.2023 12:06а что, кватновын компьютеры на практике уже ломают RSA? Часто это декларируется как "аксиома", но практических подтверждений не видел.

knstqq
30.01.2023 21:23сегодня — нет. А завтра — может быть да. И будет не очень здорово если N лет с момента появления доступных (пусть даже за 100 мильонов) квантовых компьютеров никакой криптографии с открытым ключом доверять нельзя будет.
Так что когда «на практике уже ломают RSA» будет уже поздно, притом изрядно

fryday
31.01.2023 12:09И это следствие ошибки при проектирование алгоритма. А ведь возможно спецслужбы мира уже тоже наставили бэкдоров в алгоритмах постквантового мира...



yaguarundi
50 тысяч-то дали?
Jury_78