Валерий Голованёв, Юрий Бабий

Требования к повышенной прочности, долговечности, износостойкости и плавности работы зубчатых передач были, есть и будут приоритетными при их проектировании. Примерно 80% от общего числа зубчатых передач в мировом машиностроении приходится на эвольвентные цилиндрические передачи.

В настоящее время существует несколько стандартов на исходные контуры. Каждый из них хорош по‑своему, однако получить передачу, оптимальную для заданных условий эксплуатации, при использовании стандартных подходов и методов не всегда возможно. А ведь наверняка любопытному и грамотному конструктору захочется выйти за границы стандартов, отойти от стандартного исходного контура и посмотреть — а что там? Вдруг в неведомом пока многомерном поле переменных, которыми являются исходные геометрические данные передачи, и окажется то самое решение, которое позволит в тех же габаритах создать передачу лучше и надежнее?!

Но реальность такова, что без применения современных методов оптимизации и построения корректной математической модели, описывающей работу передачи, быстро получить результат невозможно.

Для достижения цели «сделать лучше и надежнее» в программном комплексе, состоящем из расчетного модуля «Валы и механические передачи 3D» и приложения «Оптимизация IOSO‑K», реализованы IOSO‑алгоритмы оптимизации, в которых стратегия решения задач оптимизации принципиально отличается от известных подходов нелинейного программирования и базируется на новой эволюционной технологии построения поверхности отклика. Как следствие, данная технология обладает большей эффективностью, обеспечивает большие возможности.

Заложенная стратегия поиска позволяет существенно сократить количество прямых обращений к математической модели, что приводит к значимому сокращению времени, необходимого для поиска значений экстремумов.

Проведенные широкомасштабные исследования позволяют утверждать, что алгоритмы технологии оптимизации IOSO инвариантны к различным классам задач оптимизации и могут использоваться при решении проблем условной и безусловной нелинейной оптимизации в однокритериальной и многокритериальной постановках с целевыми функциями различных типов: гладкие, недифференцируемые, стохастические, с наличием областей невычисляемости, многоэкстремальные. Алгоритмы имеют высокую скорость сходимости, обладают хорошими глобальными свойствами и позволяют найти глобальный экстремум с большой степенью вероятности. В то же время алгоритмы чрезвычайно просты в использовании при постановке и решении сложных практических проблем нелинейной оптимизации и не требуют от пользователя знаний теории и методов оптимизации.

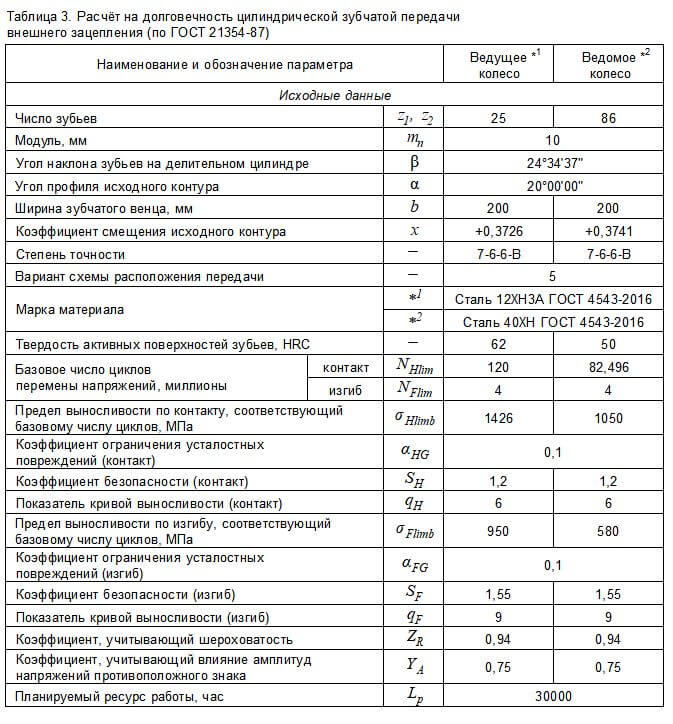
Что же в данном случае представляет собой математическая модель зубчатой передачи? По сути, это геометрический расчет, выполненный по ГОСТ 16 532–70, и расчеты на прочность и долговечность, выполненные по ГОСТ 21 354–87, с целевыми функциями, выстраиваемыми по одному или двум критериям, и системой ограничений, которая гарантирует качественные показатели зацепления. Варьируемыми параметрами в заданных диапазонах мы приняли:

1. Параметры исходного контура:

   • угол профиля;

   • коэффициент высоты головки зуба;

   • коэффициент радиального зазора;

   • коэффициент радиуса кривизны переходной кривой в граничной точке профиля зуба.

2. Коэффициенты смещения исходного контура;

3. Угол наклона зубьев на делительном цилиндре (при расчете передачи с заданным межосевым расстоянием). Он может быть как фиксированным, так и варьируемым;

4. Модуль передачи (так же может быть как фиксированным, так и вычисляемым).

Рис. 1. Варьируемые параметры

Основой системы ограничений является динамический блокирующий контур, «перестраиваемый» приложением в зависимости от варьируемых параметров передачи. Наглядным способом отображения зависимости геометрических параметров и качественных показателей передачи от коэффициентов смещения являются кривые, построенные для каждого сочетания чисел зубьев передачи z₁ и z₂ в плоской системе координат x₁ и x₂. Эта система координат была предложена М. Б. Громаном [1] еще в 1955 году, а в дальнейшем получила развитие в работах В. А. Гавриленко и коллектива, возглавляемого И. А. Болотовским. Именно В. А. Гавриленко предложил термин «блокирующий контур зубчатой передачи» — БК.

Суть блокирующего контура (рис. 1) [2] состоит в том, чтобы на плоскости координат x₁, x₂ в виде набора линий показать основные ограничения, в пределах которых будет обеспечена кинематически правильная работа зубчатой передачи.

Таковыми ограничениями (изолиниями) являются:

• Предельно допустимое минимальное значение коэффициента торцового перекрытия ε_α = 1 (при ε_α < 1 будет нарушена непрерывность зацепления зубьев в передаче). По сути, данный коэффициент можно считать критерием плавности работы;

• Интерференция в рабочем зацеплении (ситуация, когда в процессе работы передачи вершина зуба одного колеса внедряется в зуб другого колеса, т. е. происходит заклинивание зацепления);

• Границы допустимого подрезания;

• Предельно допустимое минимальное значение нормальной толщины зуба на поверхности вершин зубьев s_na = 0;

• Срезание зуба зубчатого колеса зуборезным долбяком при обработке колеса данным инструментом.

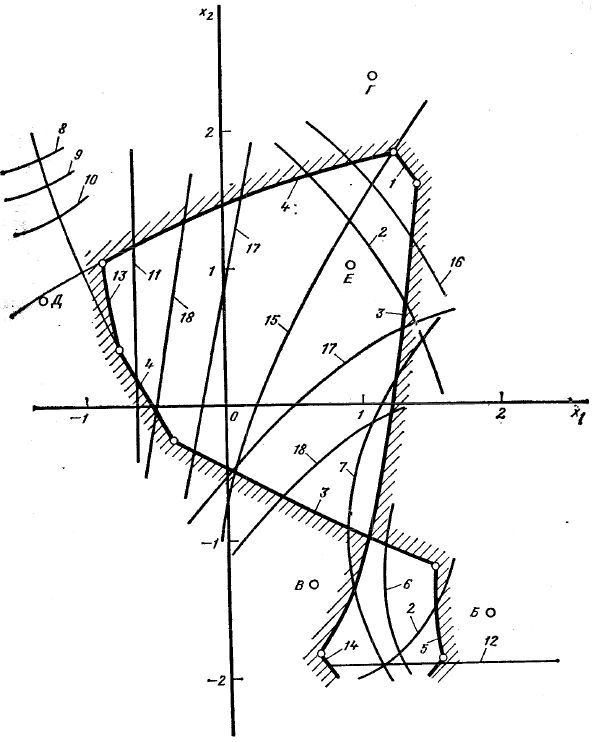
Рис. 2. Блокирующий контур передачи внешнего зацепления, составленной из колес, нарезанных реечным инструментом

Внутри блокирующего контура (БК) могут быть проведены линии условных границ, за которые переходить не рекомендуется: ε_α = 1,2, s_na = 0,4m_n, и линии x₁ = x_min1, x₂ = x_min2, ограничивающие начало подрезания, а также линия x₁ + x₂ = 0 (при расчете передачи по коэффициентам смещения) или линия x₁ + x₂ = x_Σ (при расчете передачи с фиксированным межосевым расстоянием).

Кроме того, представляет интерес линия выравнивания удельных скольжений в нижних точках активных профилей зубьев θ_p1 = θ_p2 (ЛВУС). По сути, эта линия является критерием износостойкости передачи. Применение ЛВУС в БК было сделано И. А. Болотовским [3] на основании работ Я. И. Дикера [4].

Более подробно тема использования блокирующих контуров в приложении «Валы и механические передачи» освещена в статьях [5,6,7].

В качестве критериев оптимизации могут быть использованы один или два параметра:

Рис. 3. Критерии оптимизации

Рассмотрим реальный пример. Имеем шевронную передачу редуктора колёсной пары электровоза 2ЭС5К. Цель оптимизации — повысить износостойкость передачи без изменения угла наклона зубьев и габаритных размеров.

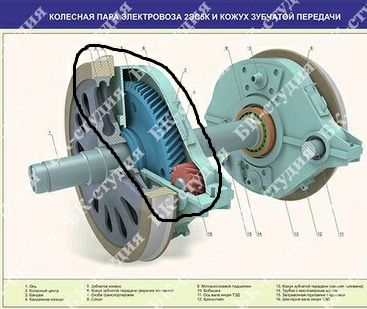
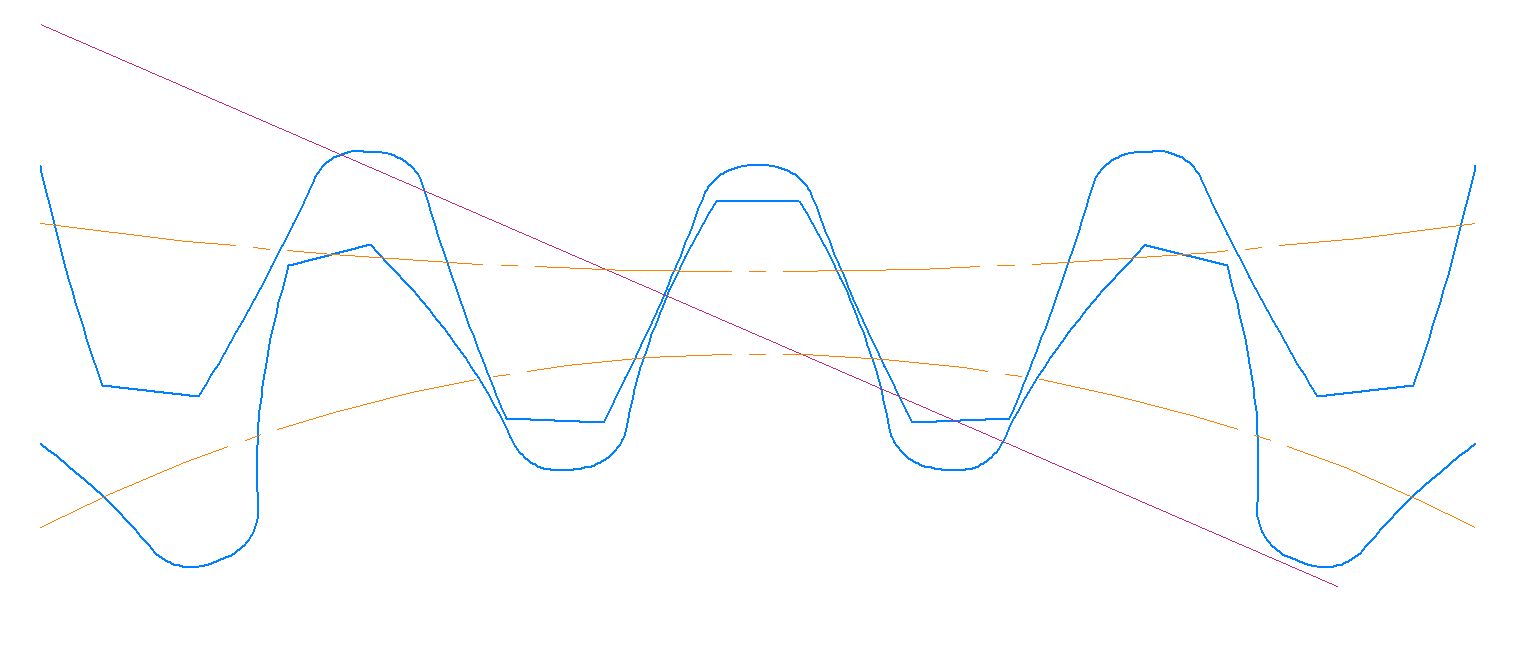
Рис. 4. Исходная передача

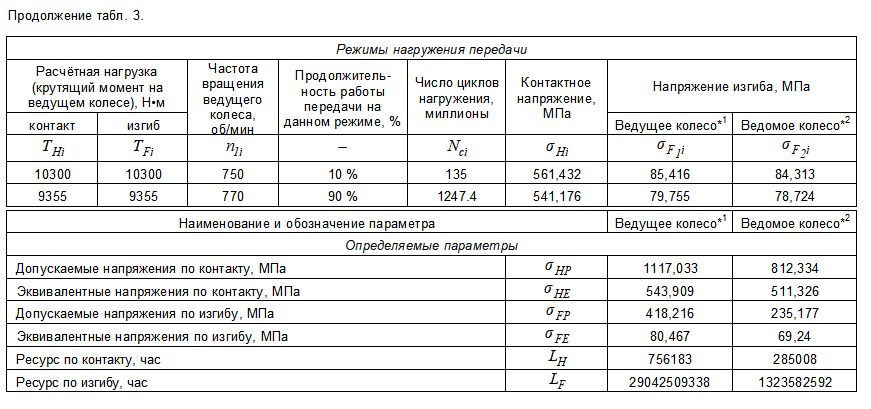
В качестве критериев оптимизации выберем износостойкость и плавность работы.

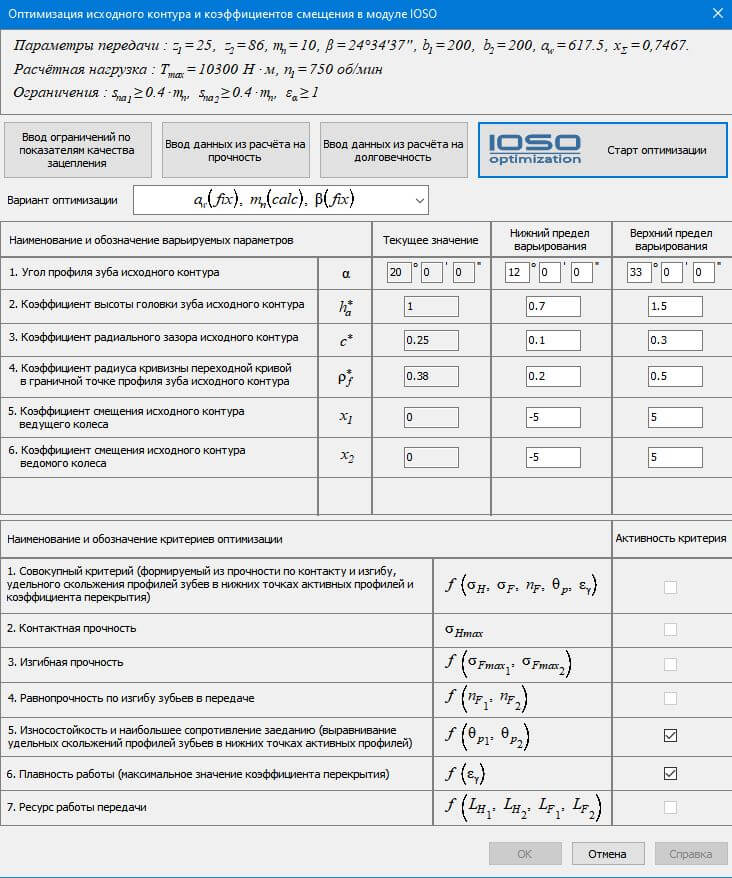
Рис. 5. Диалог приложения перед стартом оптимизации

Запускаем расчет и через некоторое время получаем его результаты в IOSO.

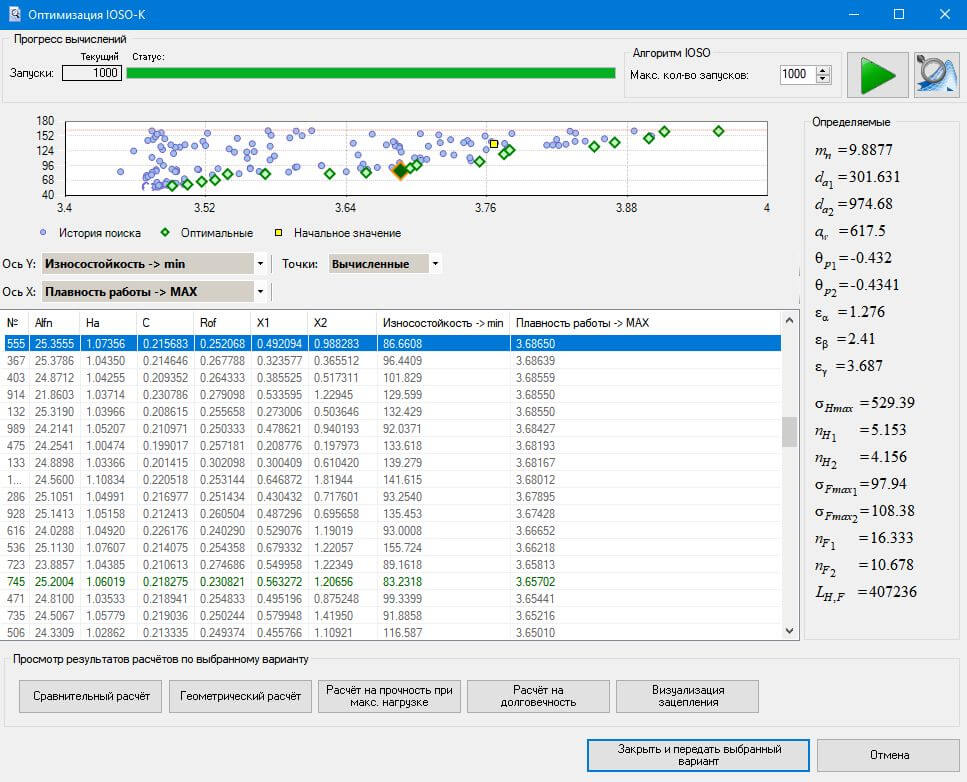
Рис. 6. Результаты расчетов в IOSO

В ходе решения задачи оптимизации получено множество Парето‑оптимальных решений (зеленые ромбы на графике), особенностью которых является то, что ни один критерий не может быть улучшен без ухудшения какого‑либо другого.

На графике по оси Y показан критерий «износ», который необходимо минимизировать, а по оси X — критерий «плавность работы», который необходимо максимизировать. Желтый квадрат на графике соответствует значениям этих критериев для исходной передачи. Анализ полученного Парето‑множества показал, что в результате решения оптимизационной задачи найдены решения, позволяющие значительно сократить износ передачи и повысить ее плавность хода по сравнению с исходным вариантом.

Мы выбрали один из вариантов. Критерием выбора в данном случае было желание выбрать нечто среднее из Парето‑множества результатов.

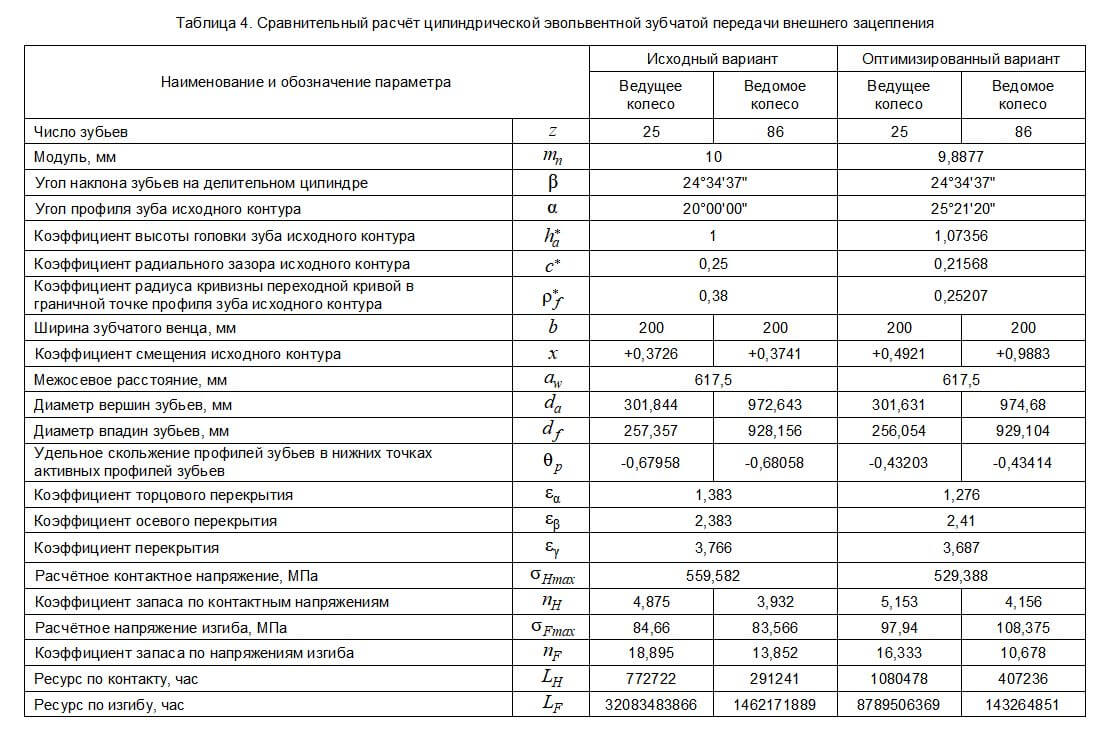
Рис. 7. Оптимизированная передача

Что мы видим... Удельное скольжение ниже, контактные напряжения ниже, ресурс передачи выше. Изгибные напряжения в данном случае нас никак не ограничивали.

Исследования можно продолжить и дальше, например, разрешить варьирование угла наклона и (или) изменить набор критериев. Но преимущества оптимизированной передачи уже очевидны.

Таким образом, применение расчетного комплекса «Валы и механические передачи 3D» в сочетании с приложением «Оптимизация IOSO‑К» в среде КОМПАС-3D открывает новые возможности в проектировании высокоэффективных зубчатых передач, обладающих наилучшими характеристиками прочности, долговечности, износостойкости и плавности.

Список ссылочной литературы

1. Гроссман М. Б., Подбор коррекции зубчатых передач. «Вестник машиностроения», № 2, 1955.

2. Болотовский И. А., Безруков В. И., Васильева О. Ф. и др., Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач. / Под ред. И. А. Болотовского. — 2-е изд. — Машиностроение, 1986. — 448 с.

3. Болотовский И. А., К вопросу о рациональном выборе коэффициентов смещения зубчатых передач. — Тр. Уфимского авиационного института. Уфа, 1957, вып. 3, с. 75–102.

4. Дикер Я. И., Таблица расчёта зацеплений зубчатых передач, Оргаметалл, 1937.

5. Голованёв В. А., Применение оптимизационных методов и интерактивного блокирующего контура при выборе коэффициентов смещения (корригировании) цилиндрических эвольвентных зубчатых передач внешнего зацепления., 23 с., http://machinery.ascon.ru/source/info_materials/2014_‑_Golovanev.pdf.

6. Голованёв В. А., Бабичев Д. Т., Использование блокирующих контуров при проектировании эвольвентных цилиндрических передач: состояние, проблемы, перспективы., 21 с., http://test.ascon.ru/source/info_materials/2014/V.%20Golovanev_and_D.Babichev.pdf.

7. Голованёв В. А., История одного зубчатого зацепления... Или как ему было без корригирования. А также небольшой экскурс к бортовой передаче танка Т-34, 15 с., https://kompas.ru/source/info_materials/2014–12_‑_toothing‑story.pdf.