Нормально разбираемся в Нормальном распределении / forpes.ru

Главная
Нормально разбираемся в Нормальном распределении

Нормально разбираемся в Нормальном распределении +41

22.04.2023 15:18

btseytlin 14 8300 Источник

Всем привет. Это пост про интуитивное понимание Нормального распределения.

Обычный курс теории вероятностей проходит следующим образом. Сначала вам даются понятные и относительно простые концепции. Все легко объясняется "на пальцах": подбрасывание монеток, красные и белые шары в урнах, кролики в клетках и так далее.

Но в следующей теме вас бросают в яму к этому монстру:

$\begin{aligned} f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp \left( -\frac{(x-\mu)^2}{2\sigma^2} \right) \end{aligned}$

Внезапно больше нет ни монет, ни урн, ни шаров. Вам только говорят запомнить эту функцию плотности вероятности Нормального распределения, что это очень важно и что график похож на колокол. В остальном вы предоставлены сами себе.

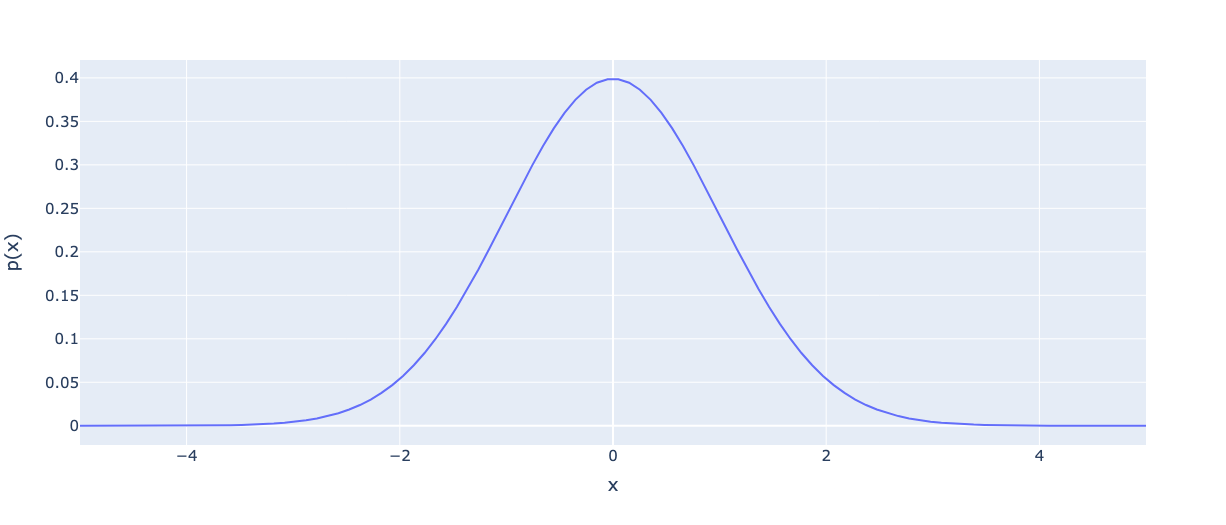
Но что это такое? Почему там экспонента? Почему минус? Зачем делить на 2 сигма-квадрат? Откуда взялось число Пи? Куда делись монеты, шары, урны и кролики? Почему мы от интуитивных объяснений перешли к тупому запоминанию?

Каждая формула несет некоторую идею. В этом посте мы будем препарировать нормальное распределение, пока не поймем, что оно в себе несет. В конце мы выведем функцию плотности вероятности, чтобы понять, откуда она берется.

Я покажу, что, несмотря на пугающий вид, Нормальное распределение это не конь в вакууме. Это все еще про броски монеток, урны и другие вещи из реального мира.

Самореклама

Эта статья является переводом моей статьи из Substack Understanding the Normal Distribution for Real. Переходите туда если вам удобнее читать на английском или хочется получать такой контент по почте.

Так же у меня есть телеграм канал @boris_again

Препарируем монстра

Начнем изнутри. Разберемся в идеях, стоящих за этим куском:

$y = -\frac{(x-\mu)^2}{2 \sigma^2}$

Режем монстра на части.

$y = (x - \mu)^2$

Где $\mu$ это среднее, один из параметров распределения.

Посмотрим на график функции $y = (x - \mu)^2$ при $\mu = 0$ :

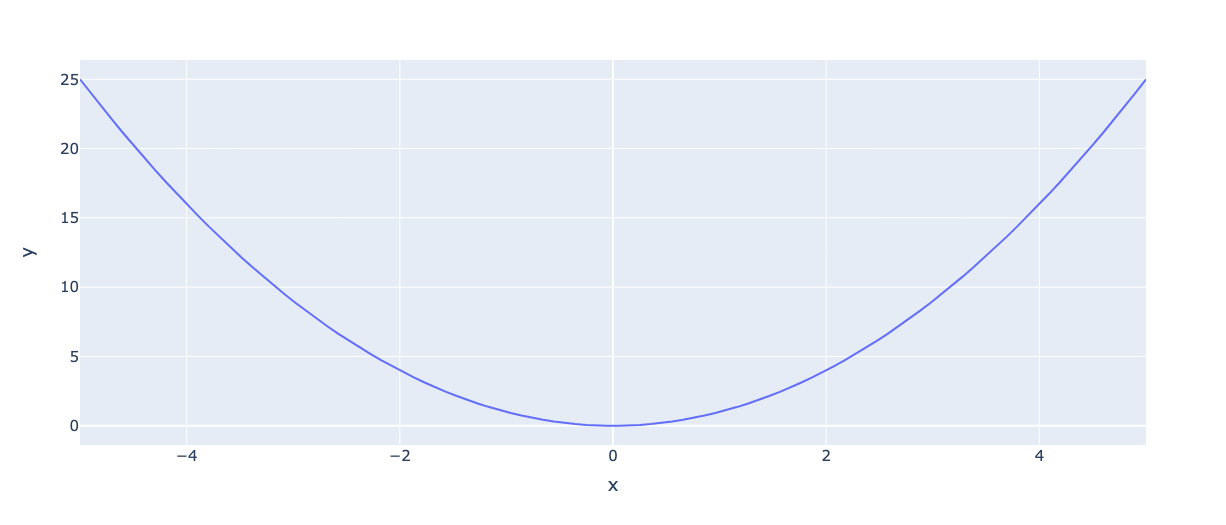
Мы видим параболу. Она похожа на форму колокола, но перевернутую. Также заметьте, что ось произвольна, а не находится в диапазоне , так что это пока не распределение.

Обратите внимание, что чем дальше от среднего значения, тем больше значение функции. Во-вторых, квадрат позволяет нам одинаково относиться к отрицательным и положительным значениям. Он делает форму колокола симметричной.

Идея: $\mu$ определяет местоположение вершины колокола, и распределение становится симметричным.

$y = -(x-\mu)^2$

Наконец-то, форма колокола! Но значения y отрицательны. Естественно у нас не может быть отрицательных вероятностей.

Что будет если менять $\mu$ ?

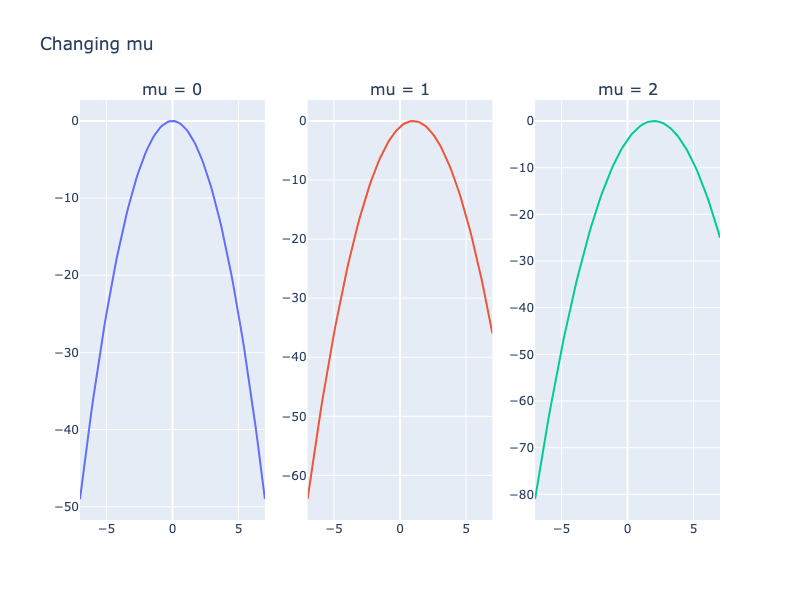
Вывод: Изменение $\mu$ перемещает пик колокола в другое место.

Добавим следующий кусок, деление на сигма квадрат:

$y = -\frac{(x-\mu)^2}{2 \sigma^2}$

Здесь сигма — это второй параметр распределения: стандартное отклонение. Квадрат сигмы — это дисперсия. Что это дает нашему распределению?

Попробуем поменять ее:

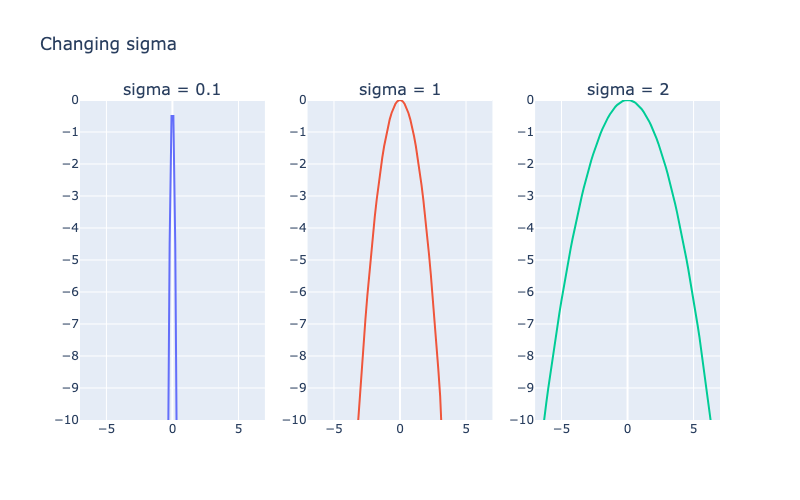
Идея: знаменатель с сигмой задает скорость изменения значения функции по мере удаления от среднего. Меньшие сигмы создают более узкие колоколообразные формы.

Мы можем рассматривать сигму как меру неопределенности. Малые сигмы указывают на то, что среднее значение более вероятно. Большие сигмы распределяют вероятность по более широкому диапазону.

Сигма возводится в квадрат, чтобы показать: неопределенность возрастает квадратично (быстро), а не линейно (медленно). Другими словами, небольшая вариация данных сильно меняет колоколообразную кривую.

Отлично, у нас есть колоколообразная кривая. Но она не похожа на распределение вероятностей. Чтобы это было распределение, выходы должны находиться в пределах и в сумме равняться 1. Вот здесь и появляется экспонента.

Давайте построим на график около нуля:

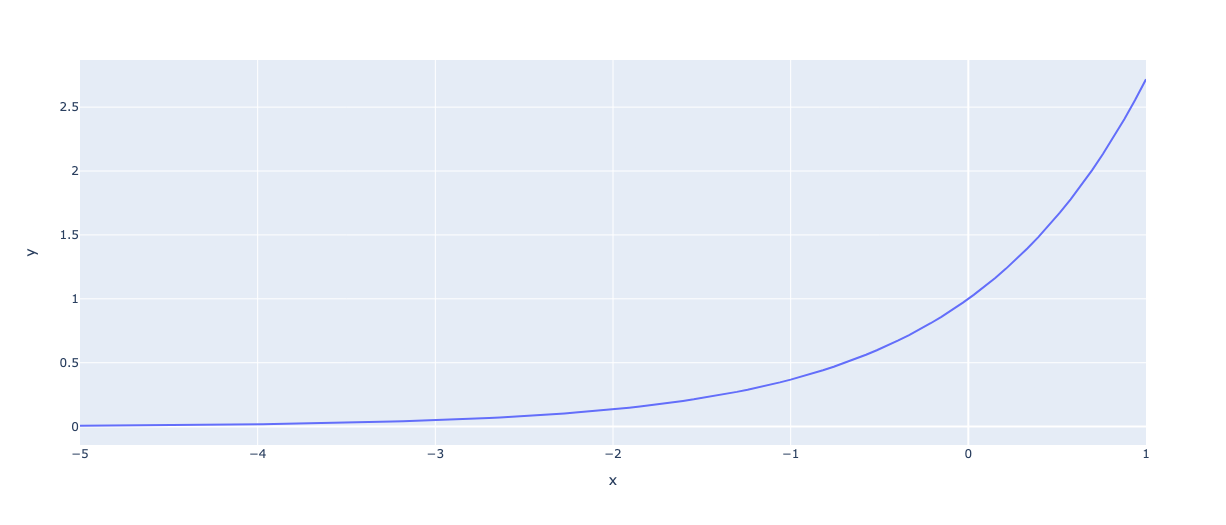
Обратите внимание: экспонента отображает любой отрицательный вход в значение между 0 и 1. В нашем случае аргумент всегда отрицательный.

$y = \exp{(-\frac{(x-\mu)^2}{2 \sigma^2})}$

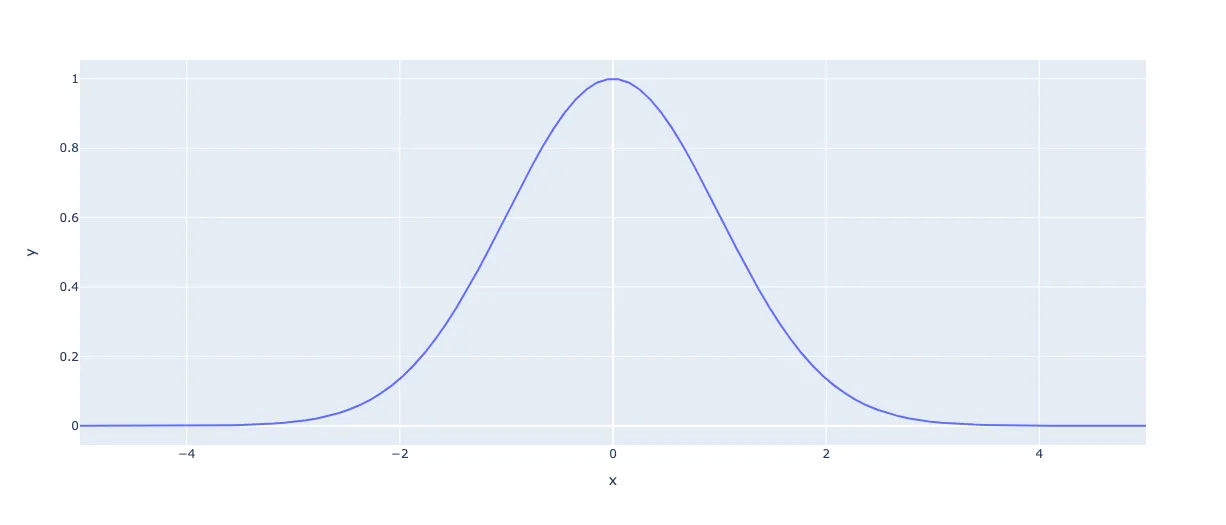
Отлично! Теперь все значения находятся между , и у нас получилась нужная нам колоколообразная кривая. Мы закончили.

На самом деле нет. Это прекрасная колоколообразная кривая, но в сумме значения не равны 1. Один только пик почти равен 1.

Как сделать так, чтобы сумма была равна 1? Нормализовать!

Как бы вы нормализовали такую последовательность чисел, как: ? Легко: разделить на сумму.

В нашем случае функция — это не просто последовательность чисел. Она непрерывна. Тем не менее, идея та же. Чтобы получить сумму давайте проинтегрируем:

$\begin{aligned} y = \int \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx = \sqrt{2\pi}\sigma \end{aligned}$

Теперь, когда у нас есть сумма, давайте разделим функцию на нее:

$y = \frac{1}{\sqrt{2 \pi}\sigma} \exp{(-\frac{(x-\mu)^2}{2 \sigma^2})}$

Наконец, мы собрали все части, чтобы получить нормальное распределение.

Если вм нужны подробности вычисления интеграла, то я рекомендую это видео:

Связь с Биномиальным распределением

Нормальное распределение тесно связано с биномиальным. Давайте отвлечемся и рассмотрим биномиальное распределение поближе. Это поможет нам получить полное представление о нормальном распределении.

Представьте, что у вас есть Substack рассылка, и вы собираетесь запустить рекламную кампанию, нацеленную на 100 человек. Вы знаете свою конверсию в подписку: 10%. Какова вероятность того, что подпишутся ровно 5 человек?

Давайте представим каждого пользователя в виде броска монеты. Он либо регистрируются с вероятностью , либо нет. Это может быть описано распределением Bernoulli(n, p), которое имеет следующую функцию массы вероятности:

$P(X=k) = \begin{cases} p & \text{if } k=1 \\ 1-p & \text{if } k=0 \\ \end{cases}$

Идея: это бросок монеты, есть два возможных исхода, и с вероятностью выпадает орел.

Это распределение позволяет отвечать на вопросы типа "Какова вероятность выпадения орла для этой монеты?" или, более практично, "Какова вероятность того, что пользователь подпишется?".

Мы можем сложить несколько случайных величин Бернулли и получить Биномиальное распределение . Оно говорит нам о вероятности получения успехов из независимых испытаний Бернулли с вероятностью .

Биномиальное распределение объединяет все независимые испытания, чтобы ответить на новые вопросы: "Какова вероятность выпадения 3 орлов из 3 бросков?" или "Сколько пользователей мы можем ожидать при регистрации?"

Вот PMF Биномиального распределения:

$\begin{aligned} f(k, n) = {n\choose k} p^k (1-p)^{n-k} \end{aligned}$

Где ${n\choose k} = \frac{n!}{k!(n-k)!}$ это Биномиальный коэффициент.

Биномиальный коэффициент используется для того, чтобы учесть множество способов регистрации человек. Например, при наличии четырех посетителей существует шесть способов зарегистрироваться двум из них.

Давайте подставим наши значения, чтобы найти вероятность того, что зарегистрируются ровно пять человек:

$\begin{aligned} f(k, n) = {100\choose 5} 0.1^5 (1-0.1)^{100-5} = 0.03387 \end{aligned}$

Ожидаемое количество подписчиков среди 5 пользователей равно просто умноженное на , то есть 3.387. Мы также можем получить вероятность регистрации хотя бы 5 подписчиков, просуммировав по $k \geq 5,$ и получим 0.94242.

Теперь давайте посмотрим, что происходит по мере роста числа испытаний.

Обратите внимание: с ростом результирующая PMF приближается к знакомой колоколообразной форме Нормального распределения.

Оказывается, что Нормальное распределение является предельным случаем биномиального распределения. Биномиальное распределение отвечает на вопрос: "Насколько вероятно получить k орлов из n бросков монеты?" Нормальное распределение имеет ту же идею, но дает приблизительный результат.

Нас интересует это приближение, потому что вычисление коэффициентов биномиального распределения для больших значений требует огромных вычислительных затрат. Факториалы в формуле являются самой большой проблемой. Например, для биномиальный коэффициент равен 75287520. Это очень дорогое вычисление, особенно если вам нужно суммировать по многим .

Вместо вычисления биномиальной PMF мы можем аппроксимировать его вычислением PDF нормального распределения. Это гораздо быстрее: нужно только подставить несколько чисел в формулу. Этот подход часто используется в опросах.

Основная идея нормального распределения: число успехов в большом количестве независимых испытаний типа "да или нет" распределено симметрично вокруг среднего значения, а форма распределения описывается функцией Гаусса.

Надеюсь, теперь PMF нормального распределения больше не является просто страшной формулой в вакууме. Она по-прежнему связана с подбрасыванием монет и реальной жизнью, как и Биномиальное распределение

Выводим Нормальное распределение

Почему именно такая функция позволяет нам аппроксимировать Биномиальное распределение? Чтобы ответить на этот вопрос, нам нужно будет вывести PMF нормального распределения. Есть несколько способов сделать это, но мы будем использовать наши знания о том, что нормальное распределение является предельным случаем биномиального распределения. Я опишу только основные шаги, так как детали вывода довольно длинные, но вы можете найти полный вывод в этой статье.

Нормальное распределение является предельным случаем Биномиального, если не очень мало, и выполняется условие:

$np \to \infty \ \text{as} \ n \to \infty$

Если это не так, мы получаем распределение Пуассона, что тоже круто, но выходит за рамки этого поста.

Помните биномиальный PMF? Предположим, у нас есть последовательность испытаний Бернулли, каждое с вероятностью успеха , и мы повторяем этот эксперимент раз. Пусть — количество успехов в n испытаниях. Тогда имеет биномиальное распределение с параметрами . Функция массы вероятности определяется как:

$\begin{equation} P(X=k) = \binom{n}{k}p^k(1-p)^{n-k} \end{equation}$

Самая тяжелая часть — факториал. Давайте воспользуемся приближением Cтирлинга, чтобы вычислить факториалы быстрее:

$\begin{equation} n! \approx n^n e^{-n} \sqrt{2\pi n}= \sqrt{2\pi n}(\frac{n}{e})^n \end{equation}$

Подставив это в Биномиальный коэффициент мы получаем:

$\begin{align} \frac{n!}{k!(n-k)!} \approx \frac{\sqrt{2\pi n}(\frac{n}{e})^n}{\sqrt{2\pi k}(\frac{k}{e})^k \sqrt{2\pi (n-k)}(\frac{n-k}{e})^{n-k}} \end{align}$

Это может выглядеть пугающе, но на самом деле это просто замена и некоторая перестановка терминов.

Подставляя это приближение в PMF Биномиального распределения, мы получаем:

$\begin{align} P(X=k) = \binom{n}{k}p^k(1-p)^{n-k} \approx \frac{1}{\sqrt{2\pi n p (1-p)}} \cdot \exp\left(-\frac{(k-np)^2}{2np(1-p)}\right) \end{align}$

Это функция плотности вероятности нормального распределения при $\mu = np$ , и квадратом $\sigma^2 = np(1-p)$ :

$\begin{equation} f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \end{equation}$

Вывод: гауссиана появляется, когда мы заменяем вычисления факториалов в биномиальном приближении.

Завершение

Мы разобрали нормальное распределение на его компоненты, исследовали связь между биномиальным и нормальным распределением и, наконец, получили нормальную PDF. Надеюсь, теперь для вас это не столько таинственный монстр, сколько прекрасный способ описания явлений реального мира.

Код для графиков вы можете найти в этом коллабе.

Спасибо за внимание! Если вам нравится такой контент, то подписывайтесь на мой телеграм канал @boris_again и substack.

Комментарии (14)

Travisw
22.04.2023 17:22
#25475788
+2
Вы как бы объяснили нормальное распределение в первой части до биноминального. Но не привели пример хотя бы и как его интерпретировать уже в готовом виде всю формулу в части монеток и шаров - связь какая?
1. 631052
  22.04.2023 17:22
  #25475902
  что 95% результатов лежат в промежутке от -2*сигма до 2*сигма
  
  а если от -3*сигма до 3*сигма уже 99.7%
  
  вы об этом?
  
  **
  
  https://www.wolframalpha.com/input?i2d=true&i=Integrate[Divide[1%2CσSqrt%5B2%CF%80%5D%5DPower%5Be%2C-Divide%5BPower%5Bx%2C2%5D%2C2Power%5B%CF%83%2C2%5D%5D%5D%2C%7Bx%2C-%CF%833%2C%CF%833%7D%5D
  1. Travisw
    22.04.2023 17:22
    #25476196
    +1
    я не пойму связь сигмы и шаров с монетками давай по проще,
    
    Это все еще про броски монеток, урны и другие вещи из реального мира.
    
    Где?
    
    Хотя бы на примере гипермонетки, то бишь игральных костей
    
    petropavel
    22.04.2023 17:22
    #25476392
    Про монетки там было. Ну если проще, подбрасываем 100 монеток, сколько будет орлов (то есть, какая вероятность получить сколько орлов)? А 1000? А 10000?
    
    Или с костями. Какая будет сумма выпавших значений (в смысле, какая вероятность у какой суммы) если бросить 100 кубиков? А 1000? А 10000?
    
    https://ru.wikipedia.org/wiki/Центральная_предельная_теорема
    
    Travisw
    22.04.2023 17:22
    #25476410
    при чем здесь сумма? у нас есть либо {0,1}, либо {1,6} или же в общем случае {a,b,...z} и тут каждая буква находится на оси абсцисс, значение по оси ординат это его вероятность и уже пляшем от этого
    
    3vi1_0n3
    22.04.2023 17:22
    #25476606
    Насколько я понял (может я не прав, конечно), тут говорится о сумме "значение на одной кости плюс значение на другой кости", что само по себе можно рассматривать как независимое событие (как и бросание монетки). При увеличении количества опытов до 100, 1000, 10000, бесконечности мы получим пределы вероятности выпадения каждой возможной суммы, которые стремятся к значению в районе 1/36. В том смысле, что стремятся стать равновероятными. Принципиально это не отличается от подбрасывания монетки. @petropavel, или вы не об этом?
    
    Travisw
    22.04.2023 17:22
    #25478440
    вопрос не о сумме был, а о шарах и монетках, а ты уплыл не туда
    
    3vi1_0n3
    22.04.2023 17:22
    #25478586
    Я конкретно про ответ petropavel и твой вопрос "при чем здесь сумма?", в котором буквально есть слово "сумма". А не про то, о чем ты раньше спросил.
    
    petropavel
    22.04.2023 17:22
    #25479574
    Ну, во первых, я говорил не о том, чтоб бросить два кубика сто раз, а сто кубиков. Или тысячу.
    
    А если бросать два, то 1/36 в пределе ну уж никак не будет. Хотя бы потому, что возможных значений всего 11 (сумма у двух кубиков — это число от 2 до 12). Но и 1/11 не будет, так как значения не равновероятные, например 7 может выпасть шестью способами, а 2 только одним.
    
    3vi1_0n3
    22.04.2023 17:22
    #25479826
    Спасибо, что объяснили, не очень понятно было. Извините, с суммами с недосыпа это я тупанул конечно.
    
    petropavel
    22.04.2023 17:22
    #25481004
    +3
    сумма — это способ объяснить попроще.
    
    подбросим монетку — есть два исхода, орёл и решка, с одинаковой вероятностью в 1/2
    
    подбросим две монетки — есть три исхода: две решки (вероятность 1/4), два орла (1/4) и один орёл + одна решка (1/2)
    
    подбросим четыре монетки — 5 вариантов. все решки (1/16), один орёл (1/4), два орла (3/8), три орла (1/4), все орлы (1/16)
    
    шесть монеток — 7 вариантов. все решки (1/64), один орёл (6/64), два орла (15/64), три орла (20/64), четыре орла (15/64), пять орлов (6/64), все орлы (1/64)
    
    вот уже вырисовывается знакомая форма. Чем больше монеток — тем ближе будет распределение к гауссиане. Это если на пальцах.
    
    thevlad
    22.04.2023 17:22
    #25476852
    +2
    Центральная предельная теорема(ЦПТ), для достаточно большой суммы независимо распределенных случайных величин(с конечной дисперсией), со средним U и дисперсией D(sigma^2), результирующее распределение будет нормальным с со средним U*n, и дисперсией D*n. Биномиальное распределение можно представить как сумму бернулливских (выпадение 0 или 1 c вероятностью p и 1-p) и применив ЦПТ получить нормальное.
    
    Вообще рассказывать про нормальное распределение и забыть про ЦПТ, как по мне довольно странно.

mentin
22.04.2023 17:22
#25476548
+2
Понятно, что большая часть вывода пропущена, но если обещаете скетч вывода, стоит хотя бы переменные объявлять. А то

Подставляя это приближение в PMF Биномиального распределения, мы получаем:

И тут в формуле всплывает q, которой раньше вообще не было. Ну то есть понятно что q это наверное 1-p, но раньше в формулах оставалось 1-p, а тут необъявленная q.
1. btseytlin Автор
  22.04.2023 17:22
  #25477022
  Вы правы, поправил, спасибо