В сегодняшнем мире доминирует индийско-арабская десятичная система. И эта система, принятая почти в каждом обществе, представляет собой то, что большинство людей считают «числами». Десятичная система оперирует числами, выраженными цифровой базой от 0 до 9. Но существуют значимые альтернативы, и они столь же разнообразны, как и культуры, к которым принадлежат. В 1994 году группа инуитских учащихся под руководством преподавателя изобрели новую систему счисления.
«Кактовикские цифры», названные в честь населённого пункта на Аляске, где они были созданы, выглядят совершенно иначе, чем цифры десятичной системы, и функционируют совсем по-другому. Они как нельзя лучше подходят для скоростной визуальной арифметики с использованием традиционной двадцатеричной системы устного счета инуитов. Особенность счёта в инупиатском языке выражается в том, что она основана на человеческом теле (с пятеричной базой). На самом деле во многих традиционных системах счёта и измерений тело человека служит математическим инструментом.
Вообще, двадцатеричная система — вторая по распространённости после десятичной. Узнать о том, в каких языках используется двадцатеричная система, можно прочитав в статье на Вики.
До определённого времени американские школы подавляли инупиатский язык, как в принципе любая система стандартизации пытается подогнать всё к своим собственным стандартам. Поэтому к 1990-м годам инупиатская система счёта была на грани забвения. Разработка кактовикских цифр начиналась как школьный проект по адаптации системы счёта к письменной форме. Система была разработана школьниками под руководством Уильяма Бартли. Числительные, основанные на счётных метках, «похожи» на инупиатские слова, которые они представляют.
Например, «таллимат» (tallimat) — слово, означающее 5, происходит от слова «рука» (талик, taliq). «Инуиньняк» (inuinnaq) — 20, представляет человека в целом.
Изначально в инупиатском языке не было слова, обозначающего 0, — тогда один из учеников предложил в качестве символа нуля использовать скрещенные над головой руки. В итоге это предложение привело к обозначению нуля в виде крестообразной метки. Набор уникальных цифр от 0 до 19 показан на рисунке и представляют собой позиционную систему счисления с основанием 20.
Вот так выглядят числа, записанные кактовикскими цифрами.
Благодаря разработанному дизайну, арифметика с использованием этих цифр поразительно наглядна. Сложение, вычитание и даже деление — почти геометрические операции, которые сводятся к добавлению или удалению символов. По сравнению с этим, арабская десятичная система выглядит очень неуклюжей. Вот так выглядят простейшие арифметические действия в кактовикской системе счисления:
Инупиатский язык часто использует визуальные знаки, а визуализация арифметики серьёзно упрощает понимание и скорость вычислений. В начале учащиеся преобразовывали математические задачи в кактовикские цифры, чтобы выполнять вычисления, но уже в 1997 году на уроках математики в Кактовике начали преподавать кактовикский счёт в равной мере с арабской десятичной системой.
После года обучения учеников в обеих системах счисления значительно вырос общий уровень подготовки школьников и стал выше среднего показателя по всем США. Такие результаты показал Калифорнийский тест успеваемости по математике. Постепенно система была одобрена советом инуитов — коллегиальным органом, представляющим интересы этого автохтонного народа, проживающего на территории Аляски, Канады, Гренландии и России.
Тем не менее в соответствии с американским федеральным законом «Ни одного отстающего ребенка» (No Child Left Behind Act) с 2002 по 2015 годы школы, преподающие эту систему счёта, столкнулись с суровыми санкциями за несоблюдение государственных стандартов, несмотря на продемонстрированное образовательное воздействие системы. Однако благодаря усилиям лингвистов из Калифорнийского университета в Беркли кактовикские цифры были введены в обновление Unicode 2022 года. До этого для обучения приходилось писать цифры от руки, либо использовать их фотографии. После текущей цифровизации системы счисления инуитов вполне возможен значительный рост интереса к этой системе, а, следовательно, и общий рост уровня подготовки учащихся.
В некотором очень уж относительном приближении визуальная арифметика с использованием кактовикских цифр схожа с одной из форм синестезии или даже савантизма. Самый известный современный пример подобной синестезии наблюдается у знаменитого саванта Дэниела Таммета. 14 марта 2004 года он воспроизвёл 22514 знаков после запятой числа Пи за 5 часов и 9 минут. Он легко и непринуждённо производит в уме сложнейшие вычисления.
«Когда я работаю с числами, я вижу две формы. Изображение начинает изменяться и развиваться, так возникает третья форма. Это и есть решение. Это похоже на математику, в которой нет необходимости думать».
Одна из самых древних и интересных систем принадлежит цивилизации майя. Эта система счисления основана на экспоненциальной двоичной последовательности чисел с основанием степени 20.
Вся последовательность записывается с использованием трёх условных обозначений: точки (единица); черты (пять); и стилизованной раковины, означающей нуль, позиционный разряд и завершенность. Эта последовательность двоичная. Именно оттого, что это двадцатеричная система, математика майя имеет сходство с двоичным кодом. Таким образом, число, стоящее в первом разряде, имеет множитель 1, во втором разряде — 20, в третьем — 400 и так далее.
Последовательность первых тринадцати членов ряда степеней 20 выглядит таким образом:
Однако в системе счета древних майя есть одно исключение. Суть его в том, что начальным числом третьего порядка является 360. Связано это исключение с астрономией и календарными вычислениями этой цивилизации, восемнадцать двадцатидневных месяцев составляли календарный год. При образовании следующих разрядов двадцатеричность снова восстанавливается.
Примеры счёта с помощью системы майя.
Одним из фактов в пользу самодостаточности майянской системы служит то, что нуль использовался в системе задолго до его широкого распространения в западноцентричной математике. Отчасти это связано с тем, что во многих культурах негативно относились к концепции «ничего». Западная философия страдала от серьёзных заблуждений о небытии. Ещё греческие мыслители говорили о том, что ничто не может существовать, поскольку говорить о чём-то — значит говорить о чем-то существующем. После появления христианства религиозные догмы утверждали, что, поскольку Бог есть во всём, что существует, всё, что ничего не представляет, должно быть сатанинским. Пытаясь спасти человечество от дьявола, они быстро изгнали «нуль», хотя торговцы продолжали тайно использовать его. Напротив, в буддизме концепция небытия не только лишена какой-либо демонической одержимости, но на самом деле является центральной идеей.
Что интересно, казалось бы, что эта система канула в историю, но это не совсем так. При подготовке этой статьи я пытался найти практические примеры применения системы майя и нашёл как минимум один похожий там, где искать специально, даже не подумал бы. Он, конечно, совсем не идентичен и вполне может быть, что я занимаюсь подгонкой фактов. Только мне кажется, что этот пример и система записи чисел майя суть явления одного корня. И разработчики этого практического применения вдохновлялись майянской системой.
Так или иначе, обратимся к наличному денежному обращению России. А именно к тактильным меткам для людей с ослабленным зрением. Впервые подобные метки появились на банкнотах 1995 года. Правда, условных обозначений было всего два: точка — единица, черта — нуль. Учитывая весь набор банкнот, было введено обозначение пятёрки в виде двух вертикально расположенных точек. После деноминации появились банкноты с сокращённым количеством нулей и метки изменились соответственно.
Мне не удалось найти документальных свидетельств влияния чисел древних майя на дизайн банкнот России, но мне нравится думать, что такая связь существовала.
При написании этого материала я множество раз отвлекался на самые разные темы, и пытался прошить какой-то красной нитью всё написанное. И главной идеей этого топика мне видится красота и многообразие математики и чисел в частности.
С нашей современной цифровой колокольни кажется, что всё тут уже давно сказано и написано. Господствующее положение не такой уж и древней десятичной системы пошатнулось с появлением машин, оперирующих другими системами счисления, хотя для рядового пользователя это и незаметно.
Существует специальный раздел математической науки, изучающий совокупность математических идей, понятий, навыков, созданных в рамках не академической математики, а национальной культуры. Этот раздел назвали этноматематикой. Она изучает отношения между математикой и культурой. Основной целью этноматематики является понимание связи между культурой и математикой. Термин «этноматематика» был введен бразильским педагогом и математиком Убиратаном Д’Амброзио в 1977 году.
Этноматематиков интересуют пути возникновения систем счисления, а также их сходства и различия. Также изучаются способы образования числовых слов. Например, в английском языке есть четыре разные системы. Немецкий и голландский языки похожи на английский, но единица ставится перед десятками в числах свыше 20. Например, «27» — это siebenundzwanzig, буквально «семь и двадцать». Во французском языке, используемом во Франции, можно увидеть некоторые различия. Soixante-dix (буквально «шестьдесят десять») — семьдесят. Слова quatre-vingt (буквально «четыре-двадцать» или 80) и quatre-vingt-dix (буквально «четыре-двадцать десять» — 90) базируются на 20 вместо 10.
Многие западноафриканские языки как и системы инуитов и майя основывают свои числовые слова на комбинации 5 и 20, полученной из представления о полной руке или полном наборе цифр, включающем пальцы рук и ног. На самом деле в некоторых языках слова для 5 и 20 относятся к этим частям тела (например, слово для 20 означает «полный человек»). В отличие от типичного счёта на пальцах, народ юки (коренные американцы из Северной Калифорнии) ведёт счёт, используя четыре промежутка между пальцами, а не сами пальцы, т. е. это уже восьмеричная, а не десятичная система счёта. Нельзя не отметить, что у этноматематики есть и противники, критика которых, в основном сводится к этичности разделения математики по национальному признаку, откуда совсем недалеко до расистских принципов. Однако на мой взгляд эти мысли мне кажутся притянутыми за уши, хотя не стоит недооценивать иногда доходящий до абсурда уровень толерантности.
Как бы то ни было не стоит забывать, что мир чисел многогранен и мышление в одной западно-эпистемологической плоскости обедняет восприятие и понимание места, в котором мы живём.
НЛО прилетело и оставило здесь промокод для читателей нашего блога:
- 15% на заказ любого VDS (кроме тарифа Прогрев) — HABRFIRSTVDS
Комментарии (25)

domix32
06.06.2023 08:36+1Есть ещё аналогичные визуальные цифры - Цистерианские. Работают по принципу обычных счёт.

Wizard_of_light
06.06.2023 08:36+7Это всё любопытно, только таблицы умножения и сложения растут как квадрат основания системы счисления. На практике в таблице умножения вместо 36 примеров (если выкинуть тривиальные умножения на 0, 1 и 10 и перестановки) для 10-ричной таблицы умножения надо будет запоминать 171 пример для 20-ричной. Ради удобства записи в отдельных примерах - так себе.

artyouhow
06.06.2023 08:36+2Так вы запоминайте умножения до 100, только в 20-ричной системе, если вам так уж угодно ????
Статья про то, что операции визуально упрощаются (в том числе и для умножения) и эффективность этого "доказана" (не проверял источники)
Кто в наше время умножает что-то сложное в уме?)

Sau
06.06.2023 08:36+2Для обучения нужно чтобы не осталось никакой магии - никакого "отсюда очевидно". Чтобы ученики могли умножать числа в двадцатеричной системе им необходимо запомнить (или просматривать) всю таблицу умножения, а не только до 100. И потом переходить к калькуляторам: не как к машинкам, которые выдают магический правильный ответ, а как у стройствам которые просто быстрее считают то же, что бы ученик мог посчитать и сам.

Wizard_of_light
06.06.2023 08:36+1По первому пункту - это так не работает, вы либо знаете таблицу умножения целиком, либо однажды внезапно понимаете, что не знаете результата умножения У на Е, и теряете время, переходя к другой системе счисления или раскладывая и считая камешки/палочки/точки в поле со сторонами У и Е элементов. И либо мы считаем что-то сложное в уме/на бумажке, либо нам визуальная простота операций не важна, а компьютер её тем более не оценит. Кстати, ради визуальной простоты я бы лучше детей двоичной системе учил - две цифры, таблица умножения и сложения из четырёх примеров, умножение и деление последовательностью простых сдвигов...

RumataEstora
06.06.2023 08:36+2Вот так выглядят простейшие арифметические действия
Это на простейших примерах. А вот V + W = Г (2 + 4 = 6, записанное с помощью более-менее похожих символов). И здесь надо учитывать "внутренний перенос разряда" при переходе между 4 и 5.
Наверно, при сложении 5 вертикальных преобразовать в 1 горизонтальную. Как в подобных случаях с другими операциями еще не сообразил.
А вот, например, как 3 + 18 = 21? Наверно, дело привычки. 6 вертикальных это 1 горизонтальная и 1 вертикальная, получается 4 горизонтальных и 1 вертикальная. А 4 горизонтальных это 1 вертикальная рядом (новый разряд).
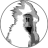
Leopotam
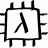
06.06.2023 08:36+3Точно так же, как и 12 разделить не на 2, а на 3 - никакой рациональной логики уже не остается как на картинке-примере. Автор выдает желаемое за действительное на удобных примерах.
leshabirukov
06.06.2023 08:36+2Это можно представить, как позиционную систему счисления, с осциллирующим основанием, - цифры с чётными номерами по основанию `5`, с нечётными - `4`. Пара таких цифр образует суперцифру с основанием `20`, в предложенной системе начертания, младшая полуцифра (по основанию `5`) это нижняя гармошка, а старшая полуцифра - верхняя.
12:2 = 6 (12 = 2*5 + 2) --> 22/2 = 11 (6 = 1*5 +1)

acsent1
06.06.2023 08:36+2Есть еще цистерианская система там можно одним знаком до 9999 числа записывать
https://facts.museum/img/facts/3821.jpg

Vytian
06.06.2023 08:36+3Лучше б они комплексные числа так кодировали: снизу вещественная, сверху боком -- мнимая часть. Сразу вся тригонометрия автоматом, а с ней и изрядный кусок классической механики и оптики. А там и до спиноров и прочих квантовых (и не очень) операторов недалеко.
Тогда, глядишь, и к "Гадким лебедям" будет шанс подобраться.


Alex500IS
白痴 - логика
MaxxONE
А что не так?
Nikeware
20-тиричная система же! Карл!
bozman
Так это двадцатеричная позиционная система счисления, 20 в десятичной будет записываться как 10.
jasiejames Автор
Совершенно верно)))
QDeathNick
Совсем запутали. 20 в десятичной будет записываться как 20, почему 10 то?
Это в двадцатеричной 20 будет записываться как 10.
jasiejames Автор
1 разряд - 1
2 разряд - множим на 20
3 разряд - на 400 и так далее.
QDeathNick
Я так и не понял к чему ваш скрин. Поясните пожалуйста, что не так по вашему?
jasiejames Автор
Человек просто невнимательно прочёл и не разобрался, а следом решил проявить чудеса логического мышления ¯\_(ツ)_/¯
pust0ta
И, замечу, начал своё сообщение со слова "идиотизм", пусть и написанного по-китайски, а как оказалось выставил идиотом себя.
jasiejames Автор
Да бог с ним. Таких персонажей достаточно, если перед каждым метать бисер времени на что-то более продуктивное и интересное не останется.