Нигерийский математик заявил о решении одной из математических «проблем тысячелетия» / forpes.ru

Главная
Нигерийский математик заявил о решении одной из математических «проблем тысячелетия»

Нигерийский математик заявил о решении одной из математических «проблем тысячелетия» +37

18.11.2015 17:52

marks 49 22000 Источник

Бернхард Риман

Профессор математики Опиеми Энох (Opeyemi Enoch) из Нигерии заявил о том, что он смог решить одну из семи математических «проблем тысячелетия». Речь идет о так называемой гипотезе Римана, над доказательством которой математики со всего мира работают вот уже 150 лет. Как говорит нам Википедия, гипотеза Римана о распределении нулей дзета-функции Римана была сформулирована Бернхардом Риманом в 1859 году. В то время как не найдено какой-либо закономерности, описывающей распределение простых чисел среди натуральных, Риман обнаружил, что количество простых чисел, не превосходящих

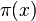, — функция распределения простых чисел, обозначаемая $\pi(x)$ — выражается через распределение так называемых «нетривиальных нулей» дзета-функции. Многие утверждения о распределении простых чисел, в том числе о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности гипотезы Римана.

Гипотеза Римана входит в список семи математических «проблем тысячелетия». За решение каждой из них Математический институт Клэя (Clay Mathematics Institute, Кембридж, Массачусетс) обещает выплатить награду в один миллион долларов США. Институт заявляет, что это делается для популяризации математики как науки, и для привлечения новых адептов этой науки из числа молодежи. В случае публикации контрпримера к гипотезе Римана, учёный совет института Клэя вправе решить, можно ли считать данный контрпример окончательным решением проблемы, или же проблема может быть переформулирована в более узкой форме и оставлена открытой (в последнем случае автору контрпримера может быть выплачена небольшая часть награды).

Формулировка гипотезы

Дзета-функция Римана $\zeta(s)$ определена для всех комплексных $s\ne 1$ и имеет нули в отрицательных чётных $s=-2,-4,-6\dots$ .
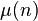из функционального уравнения $\zeta(s) = 2^s \pi^{s} \sin{\pi s \over 2} \frac1{\sin\pi s\Gamma(s)}\zeta(1-s)$ и явного выражения $\frac1{\zeta(s)}=\sum_{n=1}^\infty\frac{\mu(n)}{n^s}$ при $\operatorname{Re}\,s>1$ , где $\mu(n)$ — функция Мёбиуса, следует, что все остальные нули, называемые «нетривиальными», расположены в полосе 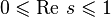$0\leqslant\operatorname{Re}\,s\leqslant1$ симметрично относительно так называемой «критической линии» ${1\over2}+i t,\; t\in\mathbb{R}$ .

Свое доказательство гипотезы нигерийский математик представил коллегам в Федеральном университете в городе Ойе-Экити. Пресс-служба этого университета уже подтвердила корректность доказательства. Ранее математик, как сообщает пресс-служба учебного заведения, работал над моделированием систем, позволяющих получать энергию звука, урагана и прибоя.

Nigerian academic solves 150-year old math problem https://t.co/6KYj4wtc2i pic.twitter.com/ZrIOaiQ40F
— This Is Africa (@ThisIsAfricaTIA) 17 ноября 2015

В Математическом институте Клэя пока что считают гипотезу Римана недоказанной. По словам представителей института, для того, чтобы достижение было зафиксировано, его необходимо опубликовать в авторитетном международном журнале, с последующим подтверждением доказательства научным сообществом.

Ранее одну из проблем тысячелетия, гипотезу Пуанкаре, доказал российский математик Григорий Яковлевич Перельман. От награды в миллион долларов он отказался.

Комментарии (49)

alltiptop
18.11.2015 21:15
#8880414
-27
По словам представителей института, для того, чтобы достижение было зафиксировано, его необходимо опубликовать в авторитетном международном журнале
У меня одного вызывает вопросы эта формулировка по поводу адекватности «института»?
1. norlin
  18.11.2015 21:26
  #8880420
  +11
  Вообще, насколько я понимаю, это единственный настоящий способ публикации научных работ. Другой вопрос, что сам институт мог бы помочь в оформлении всего этого (понятия не имею, есть ли в такой помощи смысл, или и так учёный спокойно может опубликоваться). Как минимум, есть arxiv.org, например.
  1. Sychuan
    18.11.2015 22:42
    #8880516
    +2
    Насколько я знаю, никакой особой помощи здесь не нужно. Другое дело, что статья от никому неизвестного человека может застрять в столе редакции. Но вот Чжан Итан — до этого никому неизвестный, достаточно быстро получил признание после публикации решения ослабленного варианта задачи о простых числах-близнецах
1. Coffin
  18.11.2015 21:50
  #8880444
  -26
  В реальном мире «доказано — это когда в твое доказательство верят больше, чем тех, кто не верит в него» :)
  1. forgotten
    19.11.2015 09:11
    #8880762
    +19
    Вы что-то путаете, мы здесь про математику, а не психоанализ.
    
    salas
    19.11.2015 13:11
    #8880982
    -7
    А «доказательство» — математическое понятие? Приведёте определение?
    
    BiTHacK
    19.11.2015 14:12
    #8881042
    +2
    Да, доказательство это математическое понятие из области математической логики. Вот, например, в вики по этому вопросу: ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%B4%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D1%81%D1%82%D0%B2%D0%BE
    
    ikashnitsky
    19.11.2015 15:13
    #8881114
    На сайтах ТМ есть замечательная кнопочка, чтобы прятать длинные ссылки.
    
    salas
    19.11.2015 16:15
    #8881188
    -1
    Да, любопытен проявляемый в этой статье оптимизм — «текст на естественном языке, по которому при необходимости можно восстановить формальное доказательство». Видимо, минусаторы, как и Вы, склонны отождествлять эти два понятия (доказательство и формальное доказательство) в том же духе. Но, кстати, и в этой фразе можно заметить, приглядевшись, что она задаёт психологическое понятие (что могут восстановить люди по тексту на естественном языке), а не математическое. В английской версии статьи это выражено более явно: «As practiced, a proof is expressed in natural language and is a rigorous argument intended to convince the audience of the truth of a statement.»
    
    Вообще, это в математике стандартная практика — берём общеупотребительные слова и придаём им «строгое» значение, после чего вполне себе употребляем одно и то же слово в обоих значениях. Вот, кстати, «слово» — тоже вполне себе понятие математической логики: скажем, формальное доказательство по определению является словом (одним!). Удачи в применении и этого термина при обсуждении математических статей! Но, да, это простой случай — математическое значение слова достаточно далеко от общеупотребительного, чтобы не путаться. Наоборот, «доказательство» — один из самых сложных случаев, на нём все ловятся.
    
    BiTHacK
    19.11.2015 16:41
    #8881222
    Доказательство и формальное доказательство в идеале лишь разные записи одного и того же. Отождествлять ли эти понятия? Зависит от контекста и корректности записи доказательства, но ничего страшного в таком отождествлении не вижу, если всё сделано качественно.
    
    Если вернуться к вашему высказыванию:
    
    доказано — это когда в твое доказательство верят больше, чем тех, кто не верит в него
    
    то оно значительно некорректно. Не верить в доказательство откуда-то из области религии. Если кто-то не согласен в доказательством, то, как и положено в классике, указывают либо на ошибку в рассуждениях, либо приводят контрпример. Вера тут может появиться только в том случае, если не хватает знаний для понимания доказательства.
    
    salas
    19.11.2015 17:20
    #8881240
    Это не моё высказывание. И тем, что Вы этого не заметили — хотя, полагаю, у Вас хватало для этого знаний — Вы только что лишний раз продемонстрировали, что к знаниям проверка (или вера — эти слова не просто так однокоренные, а потому что отражают разные стороны одного и того же явления) доказательств на естественном языке не сводится.
    
    BiTHacK
    19.11.2015 17:42
    #8881258
    -2
    То, что я «не заметил» в данном случае лишь невнимательность, человеческий фактор. Этот фактор как раз исключается многократной проверкой квалифицированных людей. С каждой проверкой увеличивается шанс найти несоответствие между формальным доказательством и доказательством. В данном конкретном случае хватило лишь одной проверки.
    
    salas
    19.11.2015 18:02
    #8881270
    +3
    О! Многократная проверка, именно. Осталось найти качественные отличия между многократной проверкой, которая, можно предположить, должна быть тем более многократной, чем больше сомнений, и «в твое доказательство верят больше, чем тех, кто не верит в него».
    
    И, с другой стороны, возвращаясь к вопросу о том, является ли понятие доказательства (то, которое применимо к математическим статьям) математическим: да, если таковым является понятие «квалифицированный человек».
    
    BiTHacK
    19.11.2015 18:14
    #8881288
    -1
    Качественное отличие в том, что достаточного одного того, кто не верит и аргументирует свою «неверу» контрпримером либо указанием на некорректность док-ва.
    
    salas
    19.11.2015 18:43
    #8881320
    +1
    «Аргументирует», в данном случае — точно такое же внешнее по отношению к математике понятие. Иногда ещё говорят «убедительно аргументирует» — т.е. так, чтобы это кого-то убеждало. Бывает же такое, что аргументируют неубедительно?
    
    salas
    19.11.2015 18:09
    #8881282
    +1
    И ещё деталь: несоответствие — не совсем точное слово. Квалифицированные люди в количестве тогда и нужны, когда нет готового формального доказательства, а есть только неконструктивные человеческие суждения о его существовании.
    
    MiXaiL27
    20.11.2015 04:47
    #8881674
    Пожалуйста, прекратите и дальше дискредитировать психологию и психологов! Каждый психолог с первого курса изучает высшую математику (разумеется не в том объеме, как на технических специальностях), затем переходит к мат. методам в психологии и наконец к экспериментальной психологии. Любой психолог, получивший образование в ВУЗ'е прекрасно знает что такое математическое доказательство и принципы научного метода.
    
    salas
    20.11.2015 15:35
    #8882254
    Хм, я верно понял, что Вы учились на психфаке и там говорят, что доказательство (ещё раз повторяю: то, которое обычно находится в книгах или в статьях, а не то формальное, которому оно в идеале соответствует) является объектом математики? А нас на мехмате учили, что это ваш объект. Вот прямо перед введением в ту самую науку о формальных доказательствах профессор специально это подчёркивал. Кому верить?
    
    MiXaiL27
    21.11.2015 09:24
    #8882942
    -1
    Вообще это скорее область формальной логики. Кажется это гуманитарная наука и мне очень жаль, что ей пренебрегают, как технари так и гуманитарии.
    
    Browning
    19.11.2015 14:46
    #8881088
    +5
    В каком-то смысле вы правы: доказательство и доказанность в современной математике стали довольно хитрыми понятиями, с тех пор как доказательства стали с трудом помещаться в голову одного человека (классификация простых конечных групп, ABC-гипотеза) или вообще требовать компьютер (теорема о четырёх красках).
    
    Тем не менее, если заданы набор формальных символов для записи утверждений, аксиомы и правила вывода одних утверждений из других (в виде, грубо говоря, регулярных выражений), то формально можно сказать, что доказательство — это сетка утверждений, протянутая от аксиом до нужного нам доказательства согласно правилам вывода. Другое дело, что в такой форме доказательства оказываются невозможно громоздкими, и на практике всегда «срезаются углы». Обычно — контролируемо (на основании теорем, доказанных по всем правилам), но иногда случаются и ошибки.
    
    khdavid
    19.11.2015 17:17
    #8881238
    +1
    Если быть еще более точным, то надо еще и везде добавлять «это доказательство верно, если арифметика непротиворечива». А как мы с вами знаем, еще неизвестно противоречива арифметика или нет:)
    
    forgotten
    20.11.2015 11:52
    #8881868
    Тогда уж надо ещё добавлять «и если принимать/не принимать аксиому Цермело»
1. Sychuan
  18.11.2015 22:36
  #8880504
  +29
  Наличие статьи в авторитетном международном журнале означает а) статья была проверена специалистами в данной области и они не нашли к ней существенных претензий б) с ней могут ознакомится все кто в этом заинтересован, в том числе и другие специалисты.
  Без этого мы имеем всего лишь чье-то голословное утверждение о доказательстве и подтверждение людей, о компетентности которых в данном вопросе нам ничего не известно.
  1. alltiptop
    20.11.2015 03:13
    #8881656
    Я о том что специалисты отказываются верить в доказательство потому что оно не опубликовано в журнале, а в журнале не опубликовано потому что отказываются проверять специалисты.
    
    MacIn
    20.11.2015 03:39
    #8881662
    +2
    а в журнале не опубликовано потому что отказываются проверять специалисты.
    
    Не поэтому. Если проблема сложная, проверка займет много времени.
    
    Требование публикации в мат журнале — рядовое. Так обычно и делают.
    
    alltiptop
    20.11.2015 21:11
    #8882674
    Для непосвящённого, как я, эта формулировка действительно звучит диковато.
1. Amikko
  19.11.2015 15:19
  #8881116
  -6
  Не у вас одного. Меня тоже эта фраза покоробила. Свинство.
  1. BiTHacK
    19.11.2015 16:46
    #8881224
    +5
    Вы хоть в курсе, как защищаются диссертации в РФ? Про список ВАКовских журналов в курсе? Или там свинство, тут свинство и вообще традиции в науке свинство?

ComodoHacker
18.11.2015 21:58
#8880468
+92
«Здравствуйте, %username%! Я Опиеми Энох, профессор математики из Нигерии. Недавно институт Клэя присудил мне миллион долларов, но я не могу ими воспользоваться. Помогите мне, пожалуйста, перевести их в швейцарский банк...»
1. ooprizrakoo
  19.11.2015 17:05
  #8881234
  Скроллил в ожидании такого коммента )))

ripatti
18.11.2015 22:03
#8880476
+6
Я как-раз сейчас читаю книжку Джона Дербишира "Простая Одержимость" про гипотезу Римана. Интересное совпадение.
1. nerudo
  18.11.2015 22:31
  #8880500
  +3
  Опоздали!
1. jaguard
  19.11.2015 00:34
  #8880592
  +3
  Не такое уж и совпадение, если вы примете во внимание количество посетителей ~~хабра~~, их в общем неплохой образовательный уровень и любовь к чтению. Распределение Пуассона.
1. urticazoku
  19.11.2015 07:47
  #8880730
  Тоже вспомнила эту книгу, очень интересная.
  Небольшой спойлер
  И, если не путаю, там как раз говорится, что гипотеза, возможно, никогда не будет подтверждена или опровергнута.
1. oshibka404
  19.11.2015 20:55
  #8881420
  +1
  Отличная книга. Рекомендую.

Browning
19.11.2015 02:11
#8880652
+14
Не хватает самой формулировки гипотезы: она предполагает, что все нетривиальные нули дзета-функции Римана не просто раскиданы вблизи критической линии симметрично относительно неё, а в точности все на ней лежат.

Я вот чего думаю. Другой проблемы тысячелетия, P = NP, тоже представляет собой гипотезу; и для неё существует обширный и прекраснейший список её решений, в котором (якобы доказанные) утверждения об истинности гипотезы перемежаются (якобы доказанными) утверждениями о её ложности, изредка встречаются и более экзотические варианты. Вот не пора ли для гипотезы Римана завести подобное? :)

Написал комментарий и подумал — а может, уже есть? И таки да! А самое интересное, что первая же ссылка на той странице — опровержение этой новости о нигерийском математике.
1. urticazoku
  19.11.2015 08:01
  #8880732
  +4
  Еще и плагиат (правда источник — какой-то форум):
  If, indeed, this is Opeyemi Enoch that uploaded this paper, then he is guilty of very sloppy, very blatant plagiarism. To start with, the paper doesn't even have his name on it! It has the name of Werner Raab, who (I checked) published a paper online in 2013 that is almost line for line identical to the one on Academia.edu.

forgotten
19.11.2015 09:15
#8880764
+16
Профессор Геттингенского университета Э. М. Ландау, в обязанности которого входил разбор присланных доказательств теоремы Ферма, напечатал вот такие карточки:

Уважаемый(ая)........

Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр.… в строке…. Из-за неё всё доказательство утрачивает силу.
Профессор Э. М. Ландау
1. bonext
  19.11.2015 12:45
  #8880950
  +6
  … а искать ошибки и заполнять карточки поручал своим аспирантам :)
1. urticazoku
  19.11.2015 14:36
  #8881078
  Ландау подобные сокращения видимо любил, чего стоит его «откуда очевидно» (доказательство с легкостью может занять пару страниц). Не тот.
  1. forgotten
    20.11.2015 11:47
    #8881864
    +1
    Вы путаете Льва Ландау и Эдмунда Ландау.

DanmerZ
19.11.2015 12:14
#8880922
+2
Ранее математик, как сообщает пресс-служба учебного заведения, работал над моделированием систем, позволяющих получать энергию звука, урагана и прибоя.

Энергию звука…
1. norlin
  19.11.2015 12:34
  #8880936
  +6
  Звук – это механические колебания, так что почему бы и нет…
  1. DanmerZ
    19.11.2015 12:47
    #8880954
    тогда уж энергию звука урагана и прибоя извлекать нужно, в природе мощнее звуков нет, кроме взрывов супервулканов
    
    norlin
    19.11.2015 12:48
    #8880956
    Возможно это и имелось в виду? Не смотрел оригинал… Хотя из ураганов и прибоев, ИМХО, эффективнее будет извлекать энергию как-то иначе, а не через звук.
    
    masai
    19.11.2015 20:12
    #8881402
    Смотря для чего. Не всегда требуется извлекать энергию в промышленных масштабах. Для питания какого-нибудь датчика с контроллером, возможно, хватит и пьезоэлемента.
    
    norlin
    20.11.2015 11:59
    #8881886
    А что, отличная идея для проекта на Кикстартер: пляжная зарядка для девайсов – солнечная + звуковая.
1. iUser
  20.11.2015 05:20
  #8881678
  микрофон

sev
21.11.2015 21:15
#8883228
-1
Не, ничего не доказано. К сожалению, этот профессор приписал себе чужое, но тоже неверное доказательство: aperiodical.com/2015/11/riemann-hypothesis-not-proved