Всем привет. Открываю серию статей, посвященную агрегации разметки. Этим вопросом я активно занимался, пока работал в нашем центре компетенций по работе с данными: нам нужен был механизм агрегации разметки из разных задач. По пути накопил материалов и, причесав, делюсь с вами. 

В этой части я расскажу про модель Дэвида-Скина, которая заложила основы для многих методов агрегации разметки и является второй по значимости после голосования большинством. Многие создатели проектов следуют этому методу для повышения качества данных. Изначально он был разработан в 1970-х для вероятностного моделирования медицинских обследований. Именно поэтому разберем этот метод на примере с докторами. 

Теоретические описание

Представьте ситуацию. Вы руководите командой врачей и хотите понять, кто из вашей команды самый крутой: кто точнее всех может определить симптомы со слов пациента. Сбор симптомов — вещь сложная: пациенты могут одному сказать чего-то, что не сказали другому врачу, не знают, где точно болит, и вообще когда начало болеть. Каждый врач в меру своих компетенций и интуиции определяет какой-то симптом, который он считает наиболее вероятным. Мы имеем два варианта: либо врач определит симптом правильно, либо ошибётся. 

Для оценки компетенций (крутости) врача мы можем использовать матрицу , где по одной стороне обозначим симптомы, выявленные врачом, а по другой —  истинные симптомы. Всего симптомов штук. Каждая ячейка такой матрицы показывает, насколько вероятно, что врач поставит симптом при условии, что истинным является . В оригинале, эта матрица называется individual error-rate. Обозначим такую матрицу как . Кстати, идеально крутой врач имел бы единички по диагонали.

Кто-то спросит, а откуда мне взять истинные симптомы-то для оценки? Некоторые симптомы становятся очевидными с течением времени, а какие-то можно подтвердить с помощью разных диагностик. Вот если представить, что мы набрали такие истинные симптомы и записи врачей, то рассчитать такие таблицы проще простого по формуле

Это, конечно, хорошо, но в реальности собирать все это муторно и долго, а что делать с симптомами, которые нельзя подтвердить так просто?

В поисках подходящего способа, вам приходит в голову такой мысленный эксперимент. Пусть несколько врачей спрашивают один вопрос нескольких пациентов. Необязательно, чтобы все врачи опросили всех пациентов, и один врач может задать вопрос больше одного раза. За это пусть отвечает , т. е. сколько ответов получил -ый врач от пациента . Предполагается, что ответы пациента независимы при условии истинного симптома, а также никакой врач не получает дополнительной информации.

Для начала допустим, что нам известны истинные симптомы, опять. Заимеем с потолка взявшийся теоретический индикатор , который принимает значение 1, когда врач записал истинный симптом для пациента . Да, а вероятность принципе появления пациента, у которого симптом истинен пусть будет . Зная истинные ответы, мы можем легко оценить эти вероятности, если они не известны по формуле

Тогда, прыгая сразу в карьер, для того, чтобы оценить таблицу, мы можем воспользоваться следующей оценкой правдоподобия для нашего эксперимента

Разберем по цветам:

• Красная часть — это пробег по всем пациентам,

• Синяя часть —  это пробег по всем индикаторам для каждого пациента. Из логики видим, что внутрь скобочек попадаем только если индикатор равен 1, т.е. симптом истинен.

• Не забываем также учесть вероятность этого симптома в принципе —  коричневый цвет.

• Зеленая часть —  это пробег по всем врачам.

• Желтая часть —  это оценка правдоподобия для полиномиального распределения, коим являются записанные врачами симптомы - ядро всей оценки.

Напомню, что, по определению, полиномиальное распределение —  совместное распределение вероятностей случайных величин, каждая из которых есть число появлений одного из нескольких взаимно исключающих событий при повторных независимых испытаниях. В нашем случае, записанные врачами симптомы как раз взаимоисключающие события, которые имеют совместное распределение, завязанное на враче - , когда - истинный симптом. Это нормально, если чувствуется необходимость еще раз провернуть эту мысль.

Наконец, из формулы выше, мы можем аналитически найти формулу для подсчета таблицы. Выглядеть она будет вот так

Вы описываете ваш эксперимент несколько раз своему коллеге, прежде чем до него дойдет. Осознав, он спрашивает: зачем это всё, если мы все еще должны знать истинные симптомы? Зачем нужно было городить такой огород? И вы отвечаете, что иногда, чтобы найти ответ, надо построить этот самый огород. Математики вообще очень любят так делать. И метод этот очень полезен: прежде чем копаться в том, что мы не знаем, давайте сначала сделаем для случая, когда у нас все известно. Так получается движение от простого к сложному.

Еще из этой модели мы можем узнать, как нам посчитать индикатор , имея таблицу и априорные вероятности. Сделать мы это можем по теореме Байеса

Правая часть пропорции —  это в точности часть формулы правдоподобия: коричневая - это , а зелено-желтая - остальное. Для экономии места напишу, что полная формула подсчета этой вероятности, с нормирующим знаменателем вы можете найти в статье - формула 2.5.

Теперь вы представляете, что про истинные симптомы ничего не известно, что же изменится? Если мы не знаем истинные симптомы, тогда и индикатора мы не знаем, а ведь он так удобно делал единицей все неистинные симптомы. В таком случае, мы должны учесть это незнание смесью распределений: теперь синяя часть станет суммой по всем симптомам с вероятностями этих симптом , которые мы, кстати, тоже не знаем из-за незнания индикаторов, в виде весов

Если сравнивать с предыдущей формулой, то синяя часть из произведения превратилась в сумму. И что с этим делать, непонятно, потому что для такой формы нет аналитического решения в общем виде. На помощь приходит "недавно открытый" EM-алгоритм. Вы накидываете вариант решения, и у вас получается алгоритм из следующих шагов:

1. Получить некоторые начальные значения для неизвестных параметров. В нашем случае, это индикаторы T, точнее, вероятность того, что у пациента истинный симптом при условии имеющихся у нас данных.

2. Посчитать максимальное правдоподобие интересующих значений, используя эти значения. В нашем случае, это формулы для и .

3. Провести переоценку неизвестных параметров. В нашем случае, по формуле 2.5 оцениваем вероятность для .

4. Повторить, начиная с шага 2 до сходимости.

Возвращаемся в бытие датасаентиста. Чтобы переложить модель на разметку данных, просто стоит сказать, что пациенты —  это отдельные примеры данных, врачи —  это разметчики, а симптомы —  метки классов. Как вы, возможно, уже догадались, хоть изначальный посыл подхода был в получении именно таблиц компетентности, в процессе работы мы получили вероятностные оценки истинных значений классов (симптомов). Эти значения и являются нашими агрегированными метками, хотя матрица компетентности тоже имеет ценность. Мы по ней можем оценивать работу разметчиков и выяснять, почему кто-то делает хуже или выделять группы людей, которые хороши для разметки определенных классов.

Посмотрим на код

Есть пакет Crowd-kit от Яндекс.Толоки, в котором собраны разные модели и способы агрегации, включая модель Дэвида-Скина (пост на хабре). Она реализована в классе, повторяющий интерфейс sklearn. Давайте взглянем на главную процедуру:

def fit(self, data: pd.DataFrame) -> 'DawidSkene':
    """Fits the model to the training data with the EM algorithm.
    Args:
        data (DataFrame): The training dataset of workers' labeling results
            which is represented as the `pandas.DataFrame` data containing `task`, `worker`, and `label` columns.
    Returns:
        DawidSkene: self.
    """

    data = data[['task', 'worker', 'label']]

    # Early exit
    if not data.size:
        self.probas_ = pd.DataFrame()
        self.priors_ = pd.Series(dtype=float)
        self.errors_ = pd.DataFrame()
        self.labels_ = pd.Series(dtype=float)
        return self

    # Initialization
    probas = MajorityVote().fit_predict_proba(data)
    priors = probas.mean()
    errors = self._m_step(data, probas)
    loss = -np.inf
    self.loss_history_ = []

    # Updating proba and errors n_iter times
    for _ in range(self.n_iter):
        probas = self._e_step(data, priors, errors)
        priors = probas.mean()
        errors = self._m_step(data, probas)
        new_loss = self._evidence_lower_bound(data, probas, priors, errors) / len(data)
        self.loss_history_.append(new_loss)

        if new_loss - loss < self.tol:
            break
        loss = new_loss

    probas.columns = pd.Index(probas.columns, name='label', dtype=probas.columns.dtype)
    # Saving results
    self.probas_ = probas
    self.priors_ = priors
    self.errors_ = errors
    self.labels_ = get_most_probable_labels(probas)

    return self

Как видим, на вход метод ожидает таблицу, в которой есть столбцы: 

• worker — id разметчика;

• task — id задачи;

• label — класс, который присвоил разметчик. 

После этого начальные вероятности классов для каждой задачи оцениваются с помощью метода голосования большинством, получаем априорное распределение классов, усредняя эти вероятности, и получаем первую оценку матрицу компетентности.

После этого мы попадаем в цикл, где чередуем E и M шаги. Вы, наверное, заметили, что в конце цикла считается некий evidence lower bound (она же ELBO, вариационная нижняя оценка, ВаНО) и помещается в список loss_history. Потом историю используют, чтобы прервать обучение, если разность в значении мала. 

В двух словах, ВаНО —  это оценка снизу для правдоподобия данных, когда эти данные зависят от скрытой переменной. Переводя на наш случай, данные это ответы разметчиков, а скрытые переменные — матрица компетентности и истинные метки классов. В общем виде, она определяется вот так

где - это какие-то параметры, а - распределение над . ВаНО дает нам ориентир: если она перестала расти, то мы выжали всё, что могли и можно останавливать цикл. Более подробно о выводе ВаНо и как она используется в EM-алгоритме, вы можете прочитать в этой заметке Эндрю Ына.

Завершим разбор туториалом из серии «Капитан Очевидность». В качестве датасета возьмем SNLI — это один из немногих датасетов, которые идут с разметкой от нескольких разметчиков. Для справки, каждый пример был размечен 5 разметчиками, а агрегация производилась с помощью голосования большинством. Загрузим его, выделим предложения с золотой разметкой и отдельно положим столбцы с разметкой. Преобразуем таблицу с разметкой в нужный формат.

import pandas as pd
from crowdkit.aggregation import DawidSkene

df = pd.read_csv("snli_1.0_dev.csv")
df = df.dropna()
df = df[df.gold_label != "-"]

labels = df[df.columns[-5:].to_list()]
labels = labels.reset_index()

df = df[["sentence1", "sentence2", "gold_label"]]
df.reset_index(drop=True, inplace=True)

melted_labels = labels.melt(id_vars="index", )
melted_labels.columns = ["task", "worker", "label"]

Вот так будет выглядеть таблица с разметкой:

Скормим эти данные методу и посмотрим на таблицу компетентности разметчиков:

model = DawidSkene()
agg = model.fit_predict_proba(melted_labels)
model.errors_

Можно заметить, что первый разметчик явно компетентнее всех. Давайте присоединим предсказания модели к основной таблице и посмотрим на распределение вероятностей:

agg_labels = pd.DataFrame([agg.idxmax(axis=1), agg.max(axis=1)]).T.reset_index(drop=True)
df = pd.concat([df, agg_labels], axis=1, ignore_index=True)
df.columns = ["sent1", "sent2", "gold_label", "agg_label", "proba"]
df.proba.hist()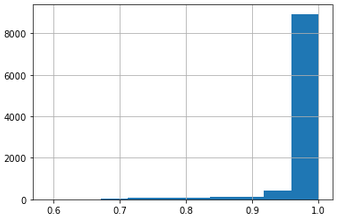

В общем, все в шоколаде. При желании можно смотреть срезы по вероятностям, чтобы понять, почему какие-то примеры имеют малую оценку. Давайте посмотрим, есть ли различия между исходной разметкой и агрегированной

diff = df[df.gold_label != df.agg_label]
print(len(diff))
# >>> 0

Чтож, это не удивительно: разметчики у нас весьма компетентны, плюс их целых пять штук. Давайте ради интереса выберем троих самых компетентных разметчиков (на мой взгляд это 1, 4 и 5), возьмем по ним агрегацию с помощью голосованиям большинством и моделью Девида-Скина и сравним с золотой разметкой.

selected_melted_labels = melted_labels[melted_labels.worker.isin(["label1", "label4", "label5"])]

from crowdkit.aggregation import MajorityVote

another_model = DawidSkene()
agg_ds = another_model.fit_predict_proba(selected_melted_labels)

mv_model = MajorityVote()
agg_mv = mv_model.fit_predict_proba(selected_melted_labels)

agg_labels_ds = pd.DataFrame([agg_ds.idxmax(axis=1), agg_ds.max(axis=1)]).T.reset_index(drop=True)
agg_labels_mv = pd.DataFrame([agg_mv.idxmax(axis=1), agg_mv.max(axis=1)]).T.reset_index(drop=True)

df = pd.concat([df, agg_labels_ds, agg_labels_mv], axis=1, ignore_index=True)
df.columns = ["sent1", "sent2", "gold_label", "agg_label_5", "proba_5", "agg_label_3_ds", "proba_3_ds", "agg_label_3_mv", "proba_3_mv"]

diff_ds = df[df.gold_label != df.agg_label_3_ds]
diff_mv = df[df.gold_label != df.agg_label_3_mv]
len(diff_ds), len(diff_mv)
# >>> (341, 354)

Сперва видим, что у нас появилось немного ошибок, 3 процента от общего числа примеров. Не так уж и критично, учитывая дороговизну разметки. Также видим, что модель Девида-Скина лишь на 13 примеров обгоняет голосование большинством. Опять же, это можно объяснить тем, что разметчики в целом хорошо делают свою работу. К сожалению, пока мне на ум не приходит, как сделать показательный пример, где бы один разметчик, например, серьезно ошибался.

Заключение

Мы рассмотрели базовую модель, которую можно использовать для оценки классов независимых примеров. Но что делать, если связи появляются, как, например, в задачах разметки последовательностей? Об этом я расскажу вам в следующий раз.