Более 9 миллиардов гигабайт информации ежедневно путешествуют по интернету, заставляя постоянно искать все новые и новые методы упаковки данных. Самые эффективные решения используют подходы, которые позволяют достичь большей плотности за счет "потерь" информации в процессе сжатия. Google, например, недавно представили вариант сжатия с потерями, в котором отправляющий компьютер отбрасывает детали изображения, а ИИ на принимающей стороне их восстанавливает. Даже Netflix использует подход, допускающий потери, понижая качество как только становится известно, что пользователь использует устройство с низким разрешением.

В то же время очень мало внимания уделяется сжатию без потерь. Почему? Ответ прост - методы сжатия без потерь уже невероятно эффективны. С их помощью работает буквально всё, от формата PNG до утилиты PKZip. И это все благодаря студенту, что захотел пропустить экзамен.

70 лет назад в MIT профессор Роберт Фано предложил своим студентам выбор: написать обычный выпускной экзамен, или улучшить ведущий алгоритм сжатия данных. Неизвестно, говорил Фано своим студентам или нет о том, что именно он является автором этого самого алгоритма, и к тому моменту уже много лет находился в поиске улучшения. Всё что нам известно это сам факт такого предложения.

Представим сообщение, собранное из букв, цифр и знаков препинания. Очевидным способом закодировать такое сообщение будет просто приписать каждому символу уникальное двоичное число. Например, символ А компьютер может представлять как 01000001, а восклицательный знак как 00100001. Подобные кодировки очень легко парсить - каждые 8 битов соответствуют одному символу. Но у них есть существенный недостаток - они отвратительно неэффективны, так, как одно и то же количество битов используется как для редких, так и для часто встречающихся в тексте символов. Многим более эффективный подход чем-то больше напоминает "морзянку", где часто встречающаяся Е представлена лишь одной точкой, а редкая Q последовательностью тире - тире - точка - тире.

Хотя код Морзе тоже довольно таки неэффективен. Да, кодировки каких-то символов короче, каких-то длиннее. Но из-за того, что длина одного символа может различаться, сообщения могут быть понятны только если между символами присутствуют небольшие периоды тишины. И действительно, без этих пауз получатель не будет иметь возможности отличить - .-. .. - . - "trite" от - .-. ..- . - "true".

Фано удалось решить эту часть проблемы. Он понял, что можно использовать коды символов различной длины без использования съедающих место "пробелов" между ними пока вы не используете одни и те же биты и для полноценного символа и для начала другого. Например, если символ S очень часто встречается в сообщении, его можно закодировать как 01, и в таком случае ни один другой код символа не должен начинаться на 01. Например, коды 010, 011, или 0110 будут все запрещены. В этом примере получившееся сообщение можно будет однозначно читать слева направо. Приписав же символу S код 01, L - 1, M - 001, и A - 000, сообщение 0100100011 можно будет однозначно расшифровать как слово "small", несмотря на то, что L представлено одним битом, S двумя, а каждая из оставшихся букв тремя.

Чтобы определять конкретные коды, Фано решил строить бинарные деревья, так, чтобы каждый символ был листом этого дерева. Код символа определялся как путь сверху вниз. Если ветка шла влево, к коду добавлялся 0, вправо - 1. Структура дерева позволяла легко избежать "перекрытия" - так, как все символы находятся в узлах - листьях, то есть окончаниях веток, ни один код не может начинаться с битов, составляющих целиком другой код.

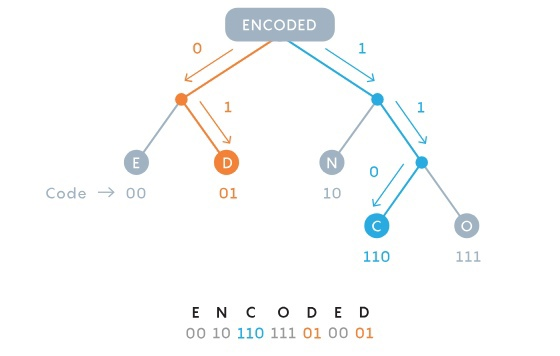
Чтобы решить, куда какие буквы должны пойти, Фано мог бы проверять каждый возможный паттерн в поиске максимально эффективного, но это было бы абсолютно непрактично. Потому он создал некое подобие алгоритма: для каждого сообщения он будет индивидуально выстраивать символы по частоте и добавлять их в дерево так, чтобы в любой паре веток символы в ветке справа использовались примерно так же часто как и символы в ветке справа. В результате, чем чаще символ встречался в тексте тем короче был бы путь до него и следовательно тем короче было бы его представление. Несколько часто встречающихся символов балансировали бы гору редких.

Это приводило к действительно эффективному сжатию. Но это не было полноценным алгоритмом, что означало, что лучшая стратегия должна существовать. Именно ее Фано и предложил найти своим студентам.

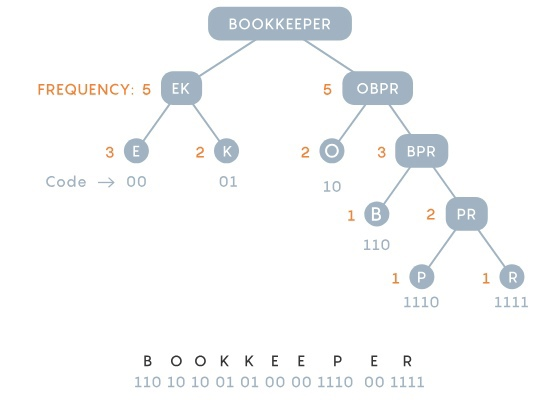
Фано строил свои деревья сверху вниз, сохраняя симметрию между парными ветками настолько, насколько это было возможно. Его студент Дэвид Хаффман перевернул этот процесс с ног на голову, строя аналогичные деревья, но снизу вверх. Хаффман решил начать с мысли, что два наиболее редких в сообщении символа должны обладать двумя самыми длинными кодами. Хаффман искал два наименее часто встречающихся символа и делал из них пару, и затем повторял процесс, выбирая два наименее встречающихся элемента из оставшихся символов и только что сформированной пары.

Теперь представим себе сообщение, в котором метод Фано проигрывает. В сообщении "Schoolroom" буква O встречается 4 раза, а S, C, H, L, R и M по одному. Подход Фано начинается с приписывания O и еще какой-нибудь буквы левой ветке, 5 использований букв из этой ветки будут соответствовать 5 использованиям букв из правой ветки. Получившееся сообщение составляет 27 бит.

Хаффман же наоборот, начинал с наименее часто встречающихся символов - например, R и M, и группировал их вместе, в дальнейшем рассматривая полученную пару как один символ.

Далее обновленный список элементов предлагает 4 варианта: O, что встречается 4 раза, пара RM, частота которой равна 2 и одиночные буквы S, H, C и L. Хаффман снова выбирает две наименее часто встречающихся элемента, допустим H и L.

Список снова обновляется: у O вес все еще 4, RM и HL имеют 2 и остались одиночные S и C. Хаффман продолжает обновлять дерево и список, на каждом шагу снова группируя вместе два самых редких элемента.

В результате "schoolroom" становится 11101111110000110110000101, что на один бит короче чем при использовании подхода Фано.

Один бит не выглядит как нечто значительное, но в масштабах миллиардов гигабайт такая небольшая экономия приносит огромный профит.

И все это благодаря тому, что Хаффман выбрал не идти на экзамен.