Мы в компании Smart Engines разрабатываем томографическое программное обеспечение и стараемся делать это как можно качественнее, без появления на изображении реконструкции визуальных искажений, так называемых артефактов. Одной из причин возникновения артефактов является несоответствие модели  формирования изображения в измерениях и модели описания данных для алгоритмов томографической реконструкции.  В классической постановке КТ описанием внутренней структуры образца служит пространственное распределение коэффициента ослабления рентгеновского излучения, причем зондирующее излучение считается монохроматическим. Однако в реальных установках это не так, существенное влияние на изменение модели формирования изображений оказывают эффекты второго порядка, одним из которых является рассеянное излучение. Что такое рассеяние, каким оно бывает и как выглядят артефакты рассеяния в томографии, -  расскажем в сегодняшней нашей статье.

Рентгеновская компьютерная томография - неинвазивный метод послойного изучения внутренней структуры объекта по его трансмиссионным (на просвет) снимкам в рентгеновском диапазоне, называемым рентгеновскими проекциями. На этапе сбора проекционных данных производится просвечивание объекта рентгеновскими лучами, исходящими из источника излучения. В рамках классической модели регистрации рентгеновских проекционных снимков, описанной в одной из наших предыдущих статей, предполагается, что все рентгеновские лучи, исходящие из источника излучения, имеют прямолинейную траекторию распространения, а интенсивность зондирующего рентгеновского излучения уменьшается экспоненциально по мере прохождения толщи изучаемого объекта согласно закону Бугера-Ламберта-Бера. Конечно, данная модель учитывает далеко не все физические феномены, сопровождающие процесс сбора проекционных данных изучаемого объекта. Одним из таких не учитываемых ранее описанной нами моделью феноменов является, например, наблюдаемое в реальных экспериментах так называемое рассеяние рентгеновского излучения.

Рассеянное излучение: теоретическая справка

Монохроматическое излучение (обладающее единой частотой волн или их малым разбросом), падающее на образец, может быть отражено, поглощено или рассеяно. Рассеянием (scattering, англ.) называется явление из­ме­не­ния на­прав­ле­ния рас­про­стра­не­ния, по­ля­ри­за­ции или час­то­ты электромагнитного из­лу­че­ния при его взаи­мо­дей­ст­вии со сре­дой. При измерении проекционных данных объекта рассеяние проявляется в отклонении траекторий распространения просвечивающих высокоэнергетических электромагнитных волн рентгеновского диапазона от классических модельных прямолинейных траекторий и сопутствующем изменении их частот (рис. 1).

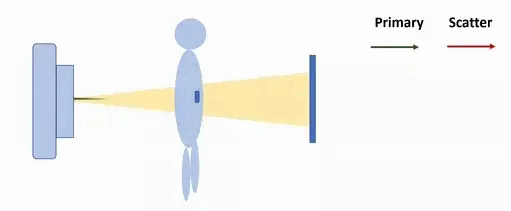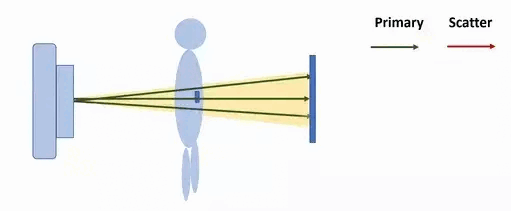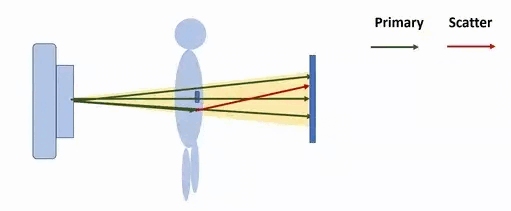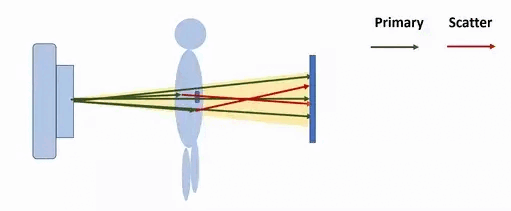
Излучение может рассеиваться либо только одним локализованным центром рассеяния (частицей, на которой происходит рассеяние, например, электроном, узлом кристаллической решетки и пр.), – это называется однократным рассеянием. Но чаще всего центры рассеяния группируются вместе; в таких случаях излучение может рассеиваться многократно, что называется многократным рассеянием (рис. 2). Основное различие между моделированием эффектов однократного и многократного рассеяния заключается в том, что однократное рассеяние обычно можно рассматривать как случайное явление, тогда как многократное рассеяние может быть смоделировано как более детерминированный процесс. Характеристики многократно рассеянного излучения могут приближенного считаться равными результатам “усреднения” соответствующих характеристик излучения в каждом из множества однократных рассеяний. Для моделирования многократного рассеяния как нельзя кстати пригождается метод Монте-Карло [1].

В физике принято различать два основных вида рассеяния:

• упругое рассеяние (или когерентное), при котором частота рассеянного излучения равна частоте излучения до рассеяния (энергия рассеянного излучения равна энергии излучения до рассеяния, т.е. выполнен закон сохранения энергии);

• неупругое рассеяние (или некогерентное), при котором частота излучения меняется при взаимодействии со средой (энергия рассеянного излучения изменяется).

Два основных вида рассеяния напоминают знакомую нам со школы задачку по физике: футбольный мяч может отскочить от поверхности футбольного поля упруго, сохранив свою скорость и отразившись от поверхности под углом, величина которого равна величине угла падения мяча (подобно законам геометрической оптики), или же, напротив, неупруго, допустим, потеряв часть своей кинетической энергии в результате трения о поверхность поля или попадания в лужу. Ситуация в мире упругого и неупругого рассеяния отчасти аналогична описанной ситуации с механикой удара мяча.

Упругое рассеяние излучения характеризуется отсутствием обмена энергией между излучением и веществом. При неупругом рассеянии между излучением и веществом может происходить перераспределение энергии, вследствие чего частота рассеянного излучения может как уменьшиться, так и увеличиться (рис. 4). Если частота рассеянного излучения меньше частоты излучения до рассеяния, то говорят о стоксовом рассеянии. В противном случае, если частота рассеянного излучения увеличивается, рассеяние именуется антистоксовым.

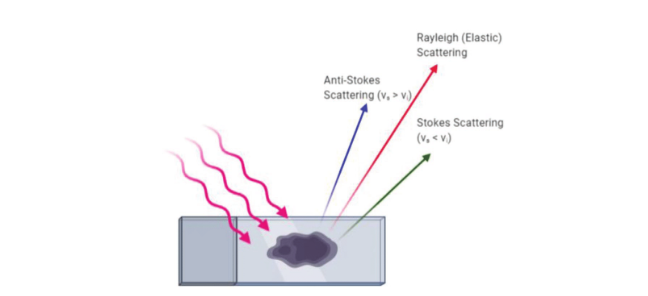
Для каждого из видов рассеянного излучения существуют большие разветвленные деревья подвидов. Отметим, что часто деление на виды и подвиды может варьироваться от автора к автору; использование отдельных терминов относительно видов упругого и неупругого рассеяния также может не являться общепринятым. 

Наиболее часто среди видов упругого рассеяния рассматривают:

• Рэлеевское рассеяние (или рассеяние Рэлея) – упругое рассеяние на малых частицах, размером меньше длины волны; рассеяние на неоднородностях.

  

• Рассеяние Ми – наблюдается в случае, когда размеры оптических неоднородностей сопоставимы с длиной волны монохроматического излучения. Теория рассеяния Ми описывает рассеяние на принципиально сферических частицах. Проявление рассеяния Ми можно наблюдать, например, в туманном лесу или сильно запыленной комнате.

  

• Рассеяние Тиндаля – рассеяние на взвешенных частицах в оптически неоднородной среде. Размеры взвешенных частиц превышают размеры атомов в десятки раз и, как правило, меньше размеров центров рассеяния Ми, но больше размеров центров рассеяния Рэлея. Рассеяние Тиндаля проявляется, когда рассеивающие свет твердые частицы диспергируются в среде, пропускающей свет. Характерно для рассеяния в коллоидных системах (разновидность дисперсной системы). Обычно наблюдается в виде светящегося конуса (конус Тиндаля), видимого на тёмном фоне (например, луч лазера).

  

• Рассеяние Томсона – упругое рассеяние электромагнитного (как правило, низкоэнергетического) излучения на свободных (несвязанных) заряженных «неполяризуемых» частицах, например, на электронах.

  

Основаниями для различия рассеяний Рэлея, Ми и Тиндаля служат тип центров рассеяния (тип частиц), их размер и концентрация (рис. 9).

С рэлеевским рассеянием мы сталкиваемся на самом деле каждый безоблачный день. Именно рэлеевским рассеянием солнечного света на неоднородностях атмосферы объясняется голубой цвет неба. Природа рассеяния Рэлея такова, что более интенсивно рассеяние коротковолнового спектра, соответствующее синей части для диапазона видимого света (рис. 10). Поэтому свет, падающий на землю под большим углом по отношению к направлению солнечного света, находится преимущественно в синей части спектра. Рассеяние Рэлея происходит в немалой степени на молекулах воздуха, размер которых намного меньше длин волн видимого света.

В пасмурную погоду, когда дневное небо затянуто тучами, поверхности земли достигает рассеянный облачными каплями солнечный свет. Поскольку размер облачных капель больше длины волны света, в данном случае имеет место рассеяние Ми вместо рассеяния Рэлея. При этом толща туч рассеивает все цвета примерно одинаково.

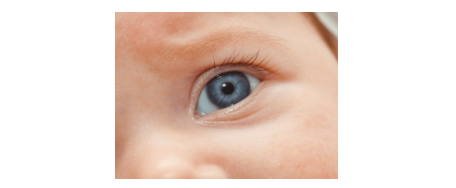
Интересным примером рассеяния Тиндаля является человеческий глаз (рис. 11). Голубая радужная оболочка глаза является голубой из-за рассеяния Тиндаля полупрозрачным слоем мутной среды в радужной оболочке, который содержит множество мелких частиц диаметром около 0,6 мкм, тонко взвешенных в фиброваскулярной структуре стромы или переднего слоя радужной оболочки. Чем больше в данном слое пигмента меланина, тем менее голубыми являются глаза человека.

Говоря же о видах неупругого рассеяния, выделяют

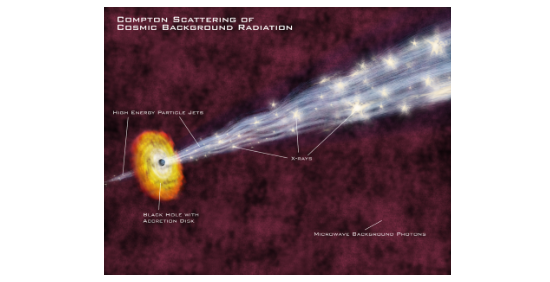
• Рассеяние Комптона – рассеяние высокоэнергетических (рентгеновских и гамма) квантов на заряженных частицах (на свободных электронах). Рассеяние Комптона учитывает релятивистские эффекты рассеяния высокоэнергетического излучения, которые в то же время пренебрегаются в рамках закона рассеяния Томсона. 

• Рассеяние Мандельштама-Бриллюэна. Данный вид неупругого рассеяния возникает при взаимодействии излучения с акустическими колебаниями решетки, или акустическими фононами (фононы – квазичастицы, введенными русским ученым И. Таммом; фонон представляет собой квант колебательного движения атомов кристалла). 

• Комбинационное (рамановское) рассеяние. Такое рассеяние излучения проявляется при взаимодействии света с другим видом фононов – оптическими.

Подчеркнем, что от рассеяния Комптона следует отличать фотоэлектрический эффект (фотоэффект). При рассеянии Комптона падающий фотон “выбивает” слабо связанный электрон из внешней валентной оболочки атома, атом ионизируется, при этом в рассматриваемой системе после столкновения с электроном существует фотон, возможно, меньшей энергии, называемый рассеянным. Направление движения рассеянного фотона, вообще говоря, не совпадает с направлением движения исходного фотона до взаимодействия с электроном. Говоря же о фотоэлектрическом эффекте, фотон полностью поглощается электроном, переходя на более высокий электронный уровень или же покидая пределы атома, падающий возбуждающий фотон при этом перестает существовать. При фотоэлектрическом эффекте рассеянного фотона не возникает (рис. 13).

Упругое рассеяние отличается от двух предыдущих взаимодействий фотона и электрона. При упругом рассеянии возбуждающий фотон взаимодействует со всем атомом как единым целым. Энергия фотона частично поглощается атомом, а оставшаяся часть энергии изначального фотона остается заключенной в рассеянном фотоне. В таком случае не высвобождается из атома электрон.  

Рассеяние в томографии

Эффекты рассеяния не обошли стороной и рентгеновскую компьютерную томографию. Помимо поглощения, тремя фундаментальными взаимодействиями рентгеновского излучения с изучаемым объектом и внешней средой, которые нельзя не учитывать, являются, в первую очередь, неупругое рассеяние Комптона, фотоэлектрический эффект и, в меньшей степени, упругое рассеяние Рэлея. Рассеянием Рэлея, а также, отчасти, фотоэлектрическим эффектом, при больших энергиях зондирующего рентгеновского излучения можно пренебречь – превалируют эффекты именно рассеяния Комптона. На рис. 14 изображено, какой вклад имеет каждое из перечисленных взаимодействий при возрастании начальной энергии распространяющегося излучения. 

Неупругое стоксово рассеяние излучения является одной из причин ослабления интенсивности излучения по мере его распространения в среде. Для всех видов такого рассеяния учет поглощения приводит к уменьшению интенсивности рассеянного излучения в направлении его падения на рассеивающую среду, что описывается экспоненциальным законом, подобным закону Бугера-Ламберта-Бера: в простейшем виде модификация закона Бугера-Ламберта-Бера, определяющего экспоненциальное ослабление интенсивности параллельного монохроматического пучка электромагнитного излучения при распространении его в поглощающей и рассеивающей среде, имеет вид

где– изначальная интенсивность излучения– координата вдоль направления распространения излучения,– интенсивность ослабленного излучения,– линейный коэффициент поглощения,– коэффициент экстинкции рассеяния, а – линейный коэффициент ослабления излучения в среде. Мы видим, что записанная формула отличается от формулы (1) в рамках классической модели без рассеяния. Как показывает практика, наличие слагаемогокритично в случае облучения высокоэнергетическим рентгеновским излучением в компьютерной томографии. Полученные в модели (1), без учета рассеяния, результаты оказываются некорректными и мало отображающими реальность, и с возрастанием энергии зондирующего излучения все меньше представляется возможным пренебрежение явлением рассеяния. Известно, что в реальных экспериментах количество рассеянных фотонов, зарегистрированных ячейкой детектора, может на порядок превышать количество первичных фотонов (отвечающих модельной прямолинейной траектории, исходящей из источника излучения) и может оставаться на уровне количества первичных фотонов даже после применения аппаратных устройств подавления рассеяния (рис. 15) [4, 5].

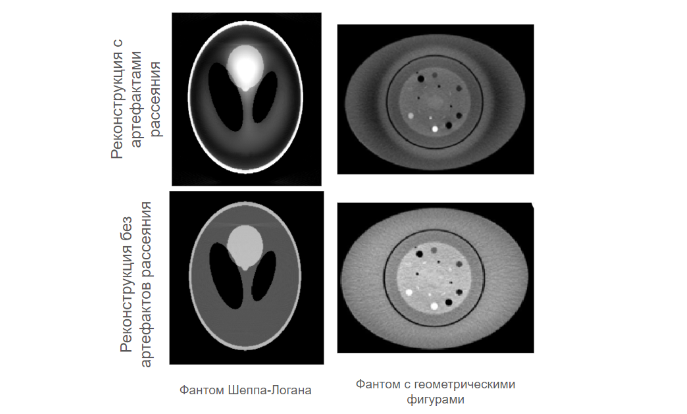
Без учета эффектов рассеяния рентгеновского излучения на реконструкции объекта появляются артефакты рассеяния (рис. 16a, 16b). Они проявляются в виде

• пространственных низкочастотных деформаций интенсивности реконструкции, известных как эффект чаши;

• полос или теней, особенно вблизи и между областями с высокой поглощающей способностью, размытия; 

• уменьшения контрастности (мягких тканей – в медицине).

Артефакты рассеяния на реконструкции также напоминают “эффект чаши”, но зачастую они более ярко выражены. Рассеяние привносит на изображение реконструкции одноименные артефакты, которые как значительно ухудшают визуальное качество изображения реконструкции, так и сильно уменьшают его точность. Изображения реконструкции с артефактами рассеяние обладают уменьшенным контрастом и не могут быть использованы для последующей корректной интерпретации и детального анализа, например, в медицинских исследованиях.

В медицине негативное влияние рассеянного излучения заключается дополнительно в том, что оно приносит весомый вред здоровью обследуемого пациента и врача-радиолога. Рассеяние Комптона, проявляющееся во время сканирования пациента, приводит к ионизации атомов тканей, клеток человека и скоплению в них свободных электронов. Рассеянное от посторонних объектов излучение, может быть, поглощено тканями организма человека, что только приводит к увеличению дозы облучения. Более того, во время обследования пациент сам становится источником рассеянного излучения, которым может быть облучен рядом находящийся врач или любой другой человек, находящийся в помещении рядом с томографом (рис. 17).

Существует несколько аппаратных подходов к подавлению артефактов рассеяния томографической реконструкции. К таким подходам относится, например, использование противорассеивающих сеток (anti-scatter grids), которые блокируют попадание значительной части рассеянных фотонов на поверхность детектора за счет уменьшения части первичного рентгеновского излучения [7]. Фильтр-”бабочка” (bow-tie filter) также помогает уменьшить регистрируемое детектором рассеяние, ограничивая поток фотонов вблизи краев объектов, где интенсивность рассеяния высока [8]. Коллимация пучка (collimator) – другой способ борьбы с рассеянием. Он позволяет “обрезать” интересующую область реконструкции и реконструировать именно ее по проекционным данным с существенно уменьшенным рассеянием (VOI – volume-of-interest). Недостатки такого подхода – появление артефактов из-за использования неполных данных объекта и, что не менее важно, ограничение скорости сканирование. Еще одним эффективным средством уменьшения рассеянного излучения является создание большого воздушного зазора (air-gap) между сканируемым объектом и детектором. Эти методы уменьшения рассеяния являются предпочтительными, так как они также уменьшают количество пуассоновского шума, добавляемого рассеянными фотонами. Однако даже при использовании таких подходов количество рассеянных фотонов, регистрируемых ячейками детектора, может достигать порядка количества нерассеянных фотонов [9].

Известны несколько программных методов для оценки и коррекции рассеяния в необработанных проекционных данных. В ряду большей части программных методов выделяют деконволюционные (или ядерные) методы (scatter deconvolution) [10, 11], методы, использующие метод Монте-Карло и другие методы моделирования [12-14]. В рамках деконволюционных методов предполагается, что рассеянное зарегистрированное детектором излучение, как (аддитивная или мультипликативная) компонента проекционного снимка, является сверткой искомого идеального проекционного снимка (без рассеяния) с некоторым ядром, называемым ядром рассеяния. Такой метод (известный также как  scatter kernel superposition, SKS) имеет преимущества, заключающиеся в том, что он не требует дополнительного оборудования, применим сразу после только одного сканирования и является эффективным с точки зрения вычислений. Но настройка этого метода для конкретного объекта исследования является крайне сложной, что обусловлено вопросом выбора подходящего индивидуального ядра рассеяния для объекта.

Вместо заключения 

Во многих прикладных применениях феномен рассеянного излучения не может быть опущен из рассмотрения. Учет рассеяния вносит свои коррективы в классические модели регистрации проекционных снимков. А пренебрежение рассеянием приводит к ухудшению качества реконструкции исследуемого объекта. И поэтому меры по подавлению рассеяния, желательно программному, должны быть предприняты. В противном случае получаемые с артефактами рассеяния изображения реконструкции просто непригодны для детального анализа. 

Среди методов уменьшения эффектов рассеяния большой востребованностью отличаются именно программные методы, поскольку даже применение аппаратных средств подавления рассеяния не позволяет полностью нивелировать его эффекты [4]. Задача же программного подавления рассеяния крайне сложна. Большая доля производителей томографического ПО не берется ее решать. Для эффективного подавления артефактов рассеяния должен быть учтен ряд факторов – компонентный состав исследуемого образца, его размеры, расположение границ компонент образца, геометрическая модель распространения рентгеновских лучей, особенности детектора и многие другие факторы. Все перечисленное делает актуальную задачу подавления рассеяния в компьютерной томографии не такой простой…

Как мы в отделе томографии Smart Engines бросаем вызов рассеянию – об этом мы расскажем вам позже. Следите за нашими новостями и обновлениями. Будем оставаться на связи, Хабр! Stay tuned! :)