Мы интуитивно понимаем, что, когда в наше поле зрения попадает небольшой предмет, на самом деле существует множество вариантов. Это может быть изначально маленький объект, находящийся рядом, объект среднего размера, находящийся на среднем расстоянии, или очень большой объект, находящийся на большом расстоянии. Именно поэтому птица, самолёт и Луна могут казаться одинакового размера в нашем поле зрения, занимая один и тот же угол на небе — то, что астрономы называют угловым диаметром, — несмотря на то, что их внутренние размеры сильно отличаются. Это простая геометрия: объект, находящийся вдвое дальше, кажется вдвое меньше, а видимый размер объекта уменьшается с увеличением расстояния до него.

Но это при условии, что геометрия Вселенной фиксирована, похожа на прямоугольную сетку и является евклидовой. В нашей реальной расширяющейся Вселенной всё не так просто, и поэтому наш читатель задаёт вопрос: как бы выглядела Андромеда или галактика размером с Андромеду, если бы мы рассматривали её в разные эпохи космической истории:

«Если бы у вас была галактика, которая была бы точно такого же размера, как галактика Андромеды, то, находясь на расстоянии до сегодняшней Андромеды, она имела бы такой же угловой размер, как сегодня. Если поместить ту же галактику ещё дальше, она будет выглядеть меньше. Но если поместить её в самые отдалённые уголки Вселенной, то она окажется близко к Большому взрыву. При этом пространство между галактиками расширяется. Поэтому, если вернуться далеко в прошлое, галактики должны быть ближе друг к другу и при этом закрывать все 360° неба. Так не начнёт ли галактика размером с Андромеду визуально “раздвигаться” и казаться очень большой?»

Удивительно, но ответ — да, если заглянуть достаточно далеко назад, то объект определённого размера, уменьшаясь в видимом угловом размере до определённого предела, снова начнёт становиться больше. Вот шокирующая научная информация о том, как это происходит.

Вы когда-нибудь подносили два пальца к глазам, смотрели на кого-то рядом и делали вид, что сминаете ему голову? Эта игра, издавна любимая детьми, работает только благодаря математике угловых размеров.

В отличие от физического размера, который является фиксированным размером твёрдого объекта, угловой размер объекта можно изменить, перемещая его ближе или дальше от вас. Линейка длиной 30 см будет казаться такой же, как и палка длиной 90 см, находящаяся в три раза дальше — так работает перспектива. Эта же концепция применима не только к любому объекту, рассматриваемому здесь, на Земле, но и в любой точке Вселенной.

Угловой размер чего угодно, от линейки до галактики, зависит как от фактического размера объекта, так и от расстояния от нас до него. Именно поэтому, когда мы измеряем объекты, расположенные очень далеко от нас, и делаем вывод о расстоянии до них — на основе того, насколько большими они кажутся нашим глазам по сравнению с их предполагаемым собственным размером, — мы называем это «расстоянием углового диаметра» [angular diameter distance]. Объекты или их совокупности, которые можно использовать для определения расстояний в космосе, астрофизики часто называют «стандартными линейками».

Вы можете наивно полагать, что размер объекта, который вы воспринимаете, зависит от его фактического размера и расстояния до вас. Если взять такой объект, как полная Луна, которая занимает на небе 0,5° на нынешнем расстоянии ~380 000 км, и переместить его в тысячу, миллион или даже миллиард раз дальше, то он займёт тысячную, миллионную или миллиардную долю своего нынешнего углового размера. Это представление разумно, но оно основано на предположении, которое большинство из нас делает, даже не задумываясь об этом: что наша Вселенная подчиняется правилам, которые устанавливает евклидова геометрия.

И это было бы верно, если бы наша Вселенная была статичной, пространственно плоской и не изменялась со временем!

Но это описание совершенно не подходит к нашей Вселенной. Напротив, наша Вселенная расширяется, причём со скоростью, которая меняется со временем. Если мы хотим понять, как измеряемый нами «угловой размер» на самом деле зависит от расстояния, необходимо принять, что наши наивные приближения работают только на малых масштабах: там, где эффекты космического расширения и его эволюции (поскольку скорость расширения меняется со временем) можно проигнорировать.

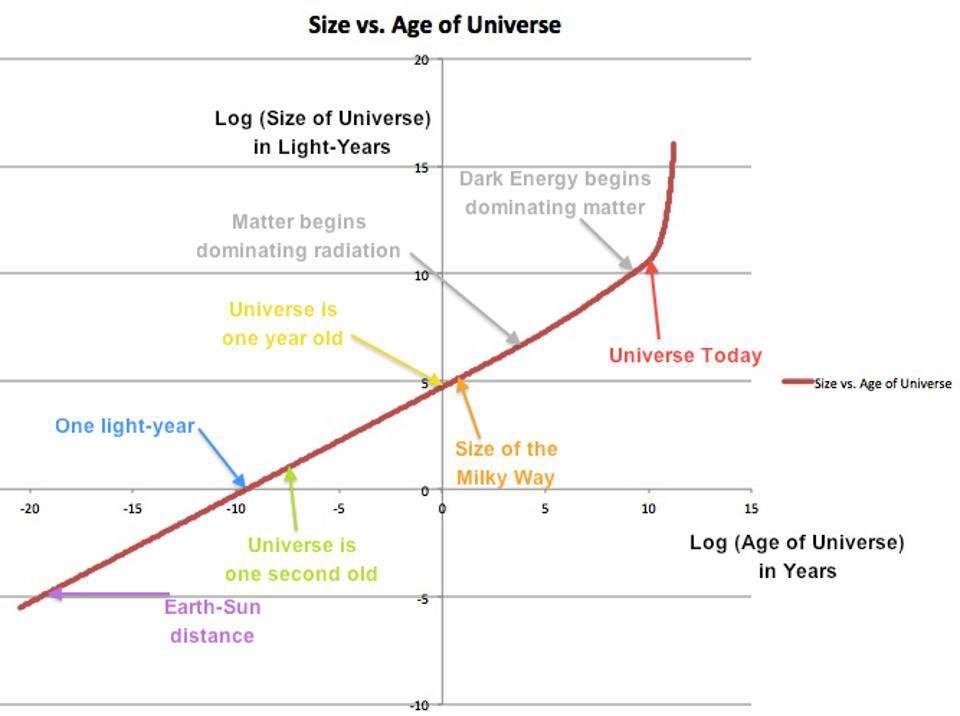
Вселенная расширяется, хотите вы этого или нет; и это факт, который был установлен наблюдениями ещё в 1920-х годах, почти 100 лет назад. В начале нашей космической истории доминирующим фактором было излучение, и плотность энергии падала по мере увеличения объёма и растяжения длины волны этого излучения. В конце концов плотность излучения упала ниже плотности материи, и во Вселенной стала доминировать материя, плотность которой зависит только от растущего объёма Вселенной. Так было с тех пор, как возраст Вселенной составлял ~9000 лет, до относительно недавнего времени: примерно 7,8 миллиарда лет после горячего Большого взрыва.

Затем, около 6 миллиардов лет назад, плотность материи, которая падала пропорционально увеличению объёма Вселенной, наконец упала ниже плотности энергии другого компонента — тёмной энергии. Поскольку тёмная энергия ведёт себя так, будто её плотность энергии постоянна, даже по мере расширения Вселенной, её влияние должно в конце концов преобладать над влиянием материи. Широкий набор доказательств подтверждает эту космическую картину, но эта постоянно меняющаяся скорость расширения влияет не только на то, насколько удалены от нас различные объекты, но и на то, насколько большими — с точки зрения углового размера — эти объекты кажутся.

Есть довольно простой способ представить себе это наглядно: представьте, что объект, на который вы смотрите, состоит из двух огоньков, расположенных на концах невидимого стержня. Если бы Вселенная, в которой вы живёте, была плоской и неизменной, угол, на который разнесены для вас эти два огонька, был бы напрямую связан с расстоянием между ними и их удалённостью от вас. Это была бы простая евклидова геометрия, где, если бы вы удвоили расстояние между вами и огнями, угловой размер, на который эти огни были разделены, уменьшился бы вдвое. Не было бы никаких эффектов, кроме эффектов простой геометрии и того, как лучи света масштабируются с расстоянием.

Но если бы вы жили во Вселенной, которая со временем меняет форму и размер — как, например, наша расширяющаяся Вселенная, состоящая из излучения, материи и тёмной энергии, — вам пришлось бы учитывать и эту эволюцию размера и формы. Вам приходится изучать пути, которые проходят отдельные фотоны, путешествуя по нашему эволюционирующему пространству-времени, и помнить об этой очень важной части головоломки: объект одного и того же размера миллиарды лет назад занимал большую часть объёма Вселенной, чем тот же объект будет занимать в более поздние времена.

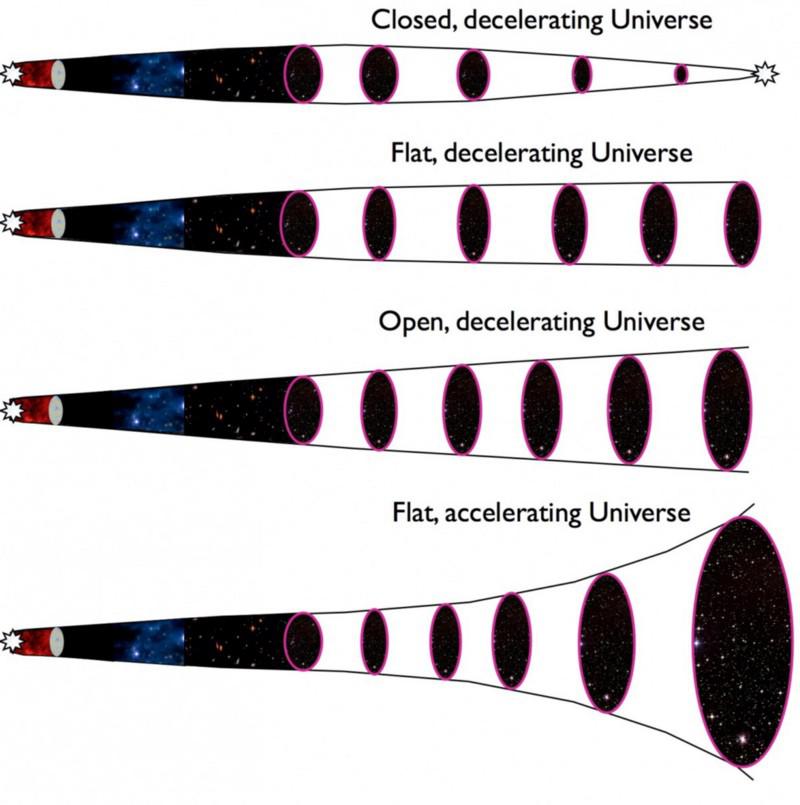
Оказывается, тип Вселенной (определяемый скоростью её расширения и относительным количеством различных типов материи и энергии, которыми она обладает) может кардинально изменить формулу, по которой видимый угловой размер объекта меняется со временем.

• Если бы у нас была статичная Вселенная, угловой масштаб объектов казался бы всё меньше и меньше, чем дальше бы они от нас удалялись, — именно так, как вы наивно ожидаете в соответствии с евклидовой геометрией: видимый размер обратно пропорционален расстоянию.

• Если бы у вас была расширяющаяся, но пустая Вселенная, это соответствовало бы Вселенной, которая линейно растёт со временем: когда вполовину более молодая Вселенная была бы вдвое меньше, чем сейчас. Когда вы рассматриваете один и тот же объект, удаляющийся от вас всё сильнее и сильнее, его видимый размер приближается к минимальному, ненулевому размеру, но никогда не уменьшается до «нулевого» даже на бесконечных расстояниях.

• Если бы у нас была расширяющаяся Вселенная, в которой не было бы ничего, кроме обычной материи, угловой масштаб удаляющегося объекта постепенно уменьшался бы по-другому, но, поскольку в прошлом Вселенная была меньше, минимальный угловой размер был бы достигнут, когда возраст Вселенной составлял бы примерно одну треть от нынешнего. После этого, поскольку Вселенная в обратной перемотке становилась меньше, плотнее и расширялась быстрее, тот же самый объект снова стал бы казаться больше.

• Однако в случае Вселенной, наполненной тёмной энергией, угловой масштаб меняется по другому принципу. Если заглядывать всё глубже в прошлое, объект определённого размера сначала будет казаться всё меньше и меньше, но только до определённого предела: когда возраст Вселенной составлял лишь четверть от нынешнего.

При выходе за эту определённую критическую точку во Вселенной, состоящей либо из материи, либо из смеси материи и тёмной энергии, объект снова начнёт казаться больше.

Если делать снимок участка небосвода с очень большой выдержкой (как, например, на приведённом выше изображении, полученном Уэббом) можно подумать, что самые маленькие галактики будут и самыми удалёнными. Если бы галактика была такого же размера, как наш Млечный Путь — около 100 000 световых лет в поперечнике — то чем дальше она от нас, тем меньше она бы казалась.

Оказалось, что это так, но только до определённого момента: до того, когда многие галактики, показанные на снимке Уэбба, уходят далеко в прошлое. В нашей Вселенной, где преобладает тёмная энергия, Млечный Путь занимал бы на небе чуть больше 2 градусов, если бы вы поместили его на то же расстояние, что и галактику Андромеды: около 2,5 миллиона световых лет. Чем дальше, тем меньше он казался бы, вплоть до минимального размера в 3,6 угловых секунды, или около 0,001 градуса.

Этот минимальный угловой размер соответствует расстоянию около 14,6 миллиарда световых лет: конечно, это большое расстояние. В нашей расширяющейся Вселенной это соответствует объекту, чей свет испытывает красное смещение около 1,5, то есть свету, чья длина волны на ~150 % больше, чем была при его испускании. Но наша наблюдаемая Вселенная простирается гораздо дальше: примерно на 46 миллиардов световых лет во всех направлениях, и самые далёкие галактики, наблюдаемые на сегодняшний день, имеют свет с красным смещением в 13,2, или растянутый на ~1320% по сравнению с тем, когда он был впервые испущен.

Мы можем подумать о Вселенной так же, как это делают астрономы: заметим, что в небе, как бы далеко мы ни заглядывали, всегда будет одинаковое количество квадратных градусов, охватывающих его с нашей перспективы. Хотя число квадратных градусов всегда остаётся постоянным (около 40 000), физические размеры, которым соответствуют эти угловые масштабы, на самом деле меняются с расстоянием.

Обычно малая угловая шкала — это одна угловая секунда (1″), что составляет 1/3600 градуса. Одна угловая секунда выглядит, как расстояние между Землёй и Солнцем, которое мы увидели бы, находясь на расстоянии одного парсека (около 3,26 световых лет). Но среди измеряемых космических величин нет «расстояния». Напрямую мы измеряем не расстояние, а красное смещение, которое мы получаем, наблюдая, насколько сильно смещены спектральные линии, универсальные для всех атомов и ионов.

Удаляясь всё дальше и дальше в прошлое, мы видим, что в 1″ укладывается всё больше парсеков (до максимума около 8 700), а максимум приходится на красное смещение ~1,5, или расстояние в ~14,6 миллиарда световых лет. За пределами этого расстояния объект того же размера будет иметь уже большие угловые размеры.

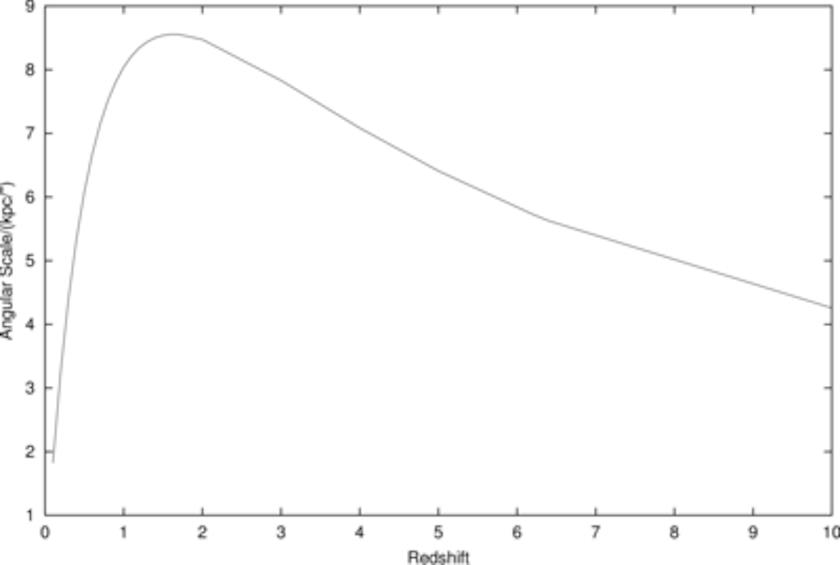
Это иллюстрирует невероятно странное явление, которое очень полезно для астрономов: если вы можете построить обсерваторию, способную получать снимки высокого разрешения галактик, находящихся на расстоянии 14,6 миллиарда световых лет (при красном смещении z=1,5), то она сможет получать снимки ещё более высокого разрешения любой галактики во Вселенной.

Одной из «обсерваторий мечты», которую астрономы надеялись когда-нибудь построить, был предложенный космический телескоп LUVOIR. В самом амбициозном варианте предполагалось вывести в космос обсерваторию с главным зеркалом диаметром 15 метров. С такой мощностью она смогла бы достичь углового разрешения около 10 угловых миллисекунд или одной сотой части угловой секунды. Телескоп с таким зеркалом всё равно разглядел бы галактики диаметром от 300 до 400 световых лет, даже галактики самого малого видимого размера, находящиеся на расстоянии 14,6 миллиарда световых лет.

Это значит, что если мы когда-нибудь построим космический телескоп такого размера, то сможем разглядеть отдельные звёздные скопления и звёздообразующие регионы размером в 300-400 световых лет и более: абсолютно все галактики такого размера в наблюдаемой части Вселенной.

Здесь кроется важный урок: длина нашей космической «линейки» действительно меняется со временем. Если смотреть в прошлое с того места, где мы сейчас находимся, то сначала кажется, что объекты становятся тем меньше, чем дальше они находятся, затем они достигают минимального углового размера, а потом снова становятся больше. Это контринтуитивный, но замечательный факт о нашей расширяющейся Вселенной.

Если вы хотите знать, насколько большим будет казаться объект в расширяющейся Вселенной, вам нужно знать не только его физический размер, но и физику того, как Вселенная расширяется со временем. Во Вселенной, которая у нас есть, состоящей на 68% из тёмной энергии, на 27% из тёмной материи, на 5% из обычной материи и примерно на 0,01% из излучения, можно сделать вывод, что объекты будут казаться всё меньше по мере удаления, пока не вступит в силу тот факт, что Вселенная в прошлом была меньше, и этот факт заставит их снова казаться тем больше, чем дальше в прошлое вы заглядываете.

Возможно, вас удивит тот факт, что когда мы рассматриваем самые удалённые галактики, такие как JADES-GS-z13-0, они кажутся в два раза больше, чем аналогичные по размеру галактики, находящиеся вдвое ближе к нам. Чем дальше мы смотрим, тем крупнее кажутся удалённые объекты. Даже без гравитационного линзирования объекты в расширяющейся Вселенной могут казаться больше на больших расстояниях, чем вы могли бы предположить!