«Нельзя быть настоящим математиком, не будучи немного поэтом»
-- Карл Вейерштрасс

История математики состоит из постоянного поиска закономерностей в волшебном и необозримом океане чисел. Учёные-романтики уже много веков бороздят этот океан в стремлении найти скрытые до поры до времени течения и водовороты, чтобы потом использовать их на благо человечества.

Математика не только универсальная, но и удивительно красивая наука. В ней древние многовековые знания органично соединяются с современными теориями и вычислениями. Многие математические задачи, которые возникли ещё до нашей эры, не имеют решения до сих пор. Эти задачи будоражат умы учёных на протяжении столетий. Невозможно предсказать, что может скрывать в себе пока не найденный ответ, какие смежные проблемы он поможет решить. Возможно, этот ответ станет ключом к новому сокровенному знанию, которое перевернёт наш мир и породит новую технологическую революцию.

В одной из таких загадок, как в зеркале, отражается вся удивительная история математики. Эта задача связана с рядом чисел, которые ещё в глубокой древности называли «совершенными» (др.-греч. ἀριθμὸς τέλειος). Последующие поколения математиков добавляли в копилку знаний человечества новые числа этого ряда. Процесс ещё не окончен, поиски продолжаются. Кроме того, с совершенными числами связано много тайн и не разрешённых до сих пор загадок. Что же в них такого особенного?

Сверкающие звёзды в огромной бездне чисел

Для начала немного теории. Натуральное число считается совершенным, если оно равно сумме своих делителей, отличных от самого числа. Самое маленькое совершенное число — 6 = 1 + 2 + 3. Следующее совершенное число — 28 = 1 + 2 + 4 + 7 + 14. Дальше идут числа 496 и 8128.

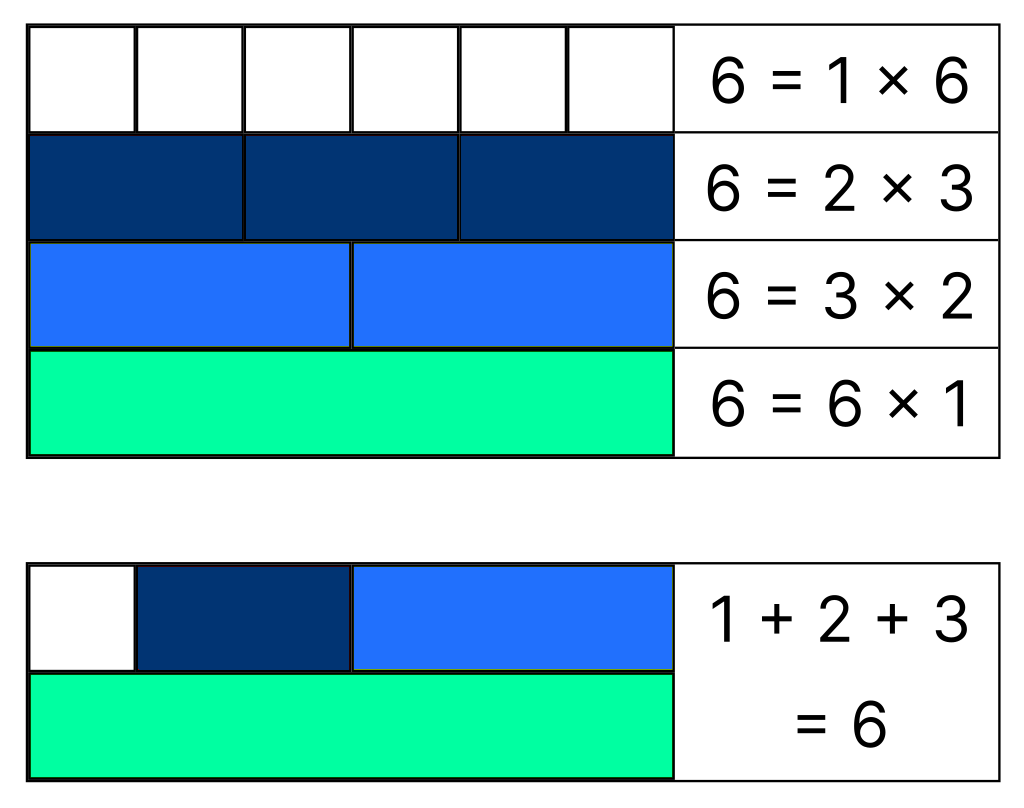
Почему же эти числа называют «совершенными»? Ведь существует ещё множество других интересных чисел с не менее выдающимися свойствами. Но для древнегреческих философов-пифагорейцев эти числа были самыми красивыми, самыми особенными из всех. Для них они были подобны сверкающим звёздам в бесконечном числовом мире. И действительно, совершенных чисел совсем немного — это штучное явление. А всё то, что красиво и редко встречается, привлекает особое внимание.

Например, древнегреческий философ и математик Никомах Герасский писал: «Совершенные числа красивы. Но известно, что красивые вещи редки и немногочисленны, безобразные же встречаются в изобилии. Избыточными и недостаточными являются почти все числа, в то время как совершенных чисел немного».

Кроме того, для многих древних народов, культур и религий числа «6» и «28» имели глубокий символический смысл. В Древней Греции шестое место на званых пирах считалось самым почётным, его занимал самый уважаемый гость. В Библии написано, что мир был сотворён за 6 дней. Много внимания этому числу уделил и Платон в своих «Диалогах».

Число «28» — тоже не такое простое, как может показаться. Например, неопифагорейская академия наук состояла из 28 членов. До недавнего времени по обычаю столько же членов должны были входить в различные учёные общества. Да и лунный месяц составляет около 28 дней.

Все дороги ведут к простым числам

До Евклида древние математики не знали других совершенных чисел, кроме 6 и 28. Но великий основатель геометрии доказал, что совершенное число можно представить в виде произведения множителей 2^p−1 и 2^p−1, причём второй множитель должен быть простым числом. С этим последним условием возникло больше всего сложностей. Во многом именно из-за него история совершенных чисел не завершена до сих пор.

Для p = 2 получаем первое совершенное число: 2²⁻¹ × (2²−1) = 6. Второе совершенное число 28 соответствует p = 3. Благодаря своей формуле, Евклид нашёл ещё два совершенных числа: 496 — для p = 5 и 8128 для p = 7.

После этого дело застопорилось на много веков. Долгое время никому не удавалось вычислить пятое совершенное число. Никто даже не мог сказать, существует ли оно вообще. А ведь в те времена люди верили, что тому, кто найдёт следующее совершенное число, уготовано вечное блаженство. Несмотря на столь заманчивое обещание, никто так и не смог это сделать за полторы тысячи лет.

Это и не удивительно. Ведь пятое совершенное число намного больше четвёртого — 33 550 336. Его отыскали только в XV веке. Сначала считалось, что это сделал голландский математик Худалрик Региус в 1536 году. Но потом историки обнаружили неопубликованную рукопись немецкого математика, астронома и астролога Региомонтана, датированную 1461 годом. В ней содержалось пятое совершенное число. Оно тоже подчинялось формуле Евклида для p = 13.

После этого стало понятно, что каждое последующее совершенное число гораздо больше предыдущего. Поэтому поиск очередного совершенного числа для каждого поколения математиков превращался в нетривиальную задачу. Рене Декарт по этому поводу метко заметил, что «совершенные числа, как и совершенные люди, встречаются редко».

Таинственное прозрение европейских математиков

Ещё через 200 лет в раскрытии тайны совершенных чисел поучаствовал французский математик и музыкант Марен Мерсенн. В XVII веке он был, по существу, координатором научной жизни Европы, вёл активную переписку практически со всеми видными учёными того времени: Галилеем, Паскалем, Торричелли и многими другими. Ещё он был другом Декарта и Ферма, а также являлся одним из основателей Парижской академии наук.

Неудивительно, что Мерсенн заинтересовался совершенными числами, которые будоражили умы математиков уже не одно столетие. В 1644 году он опубликовал сочинение "Cogitata physico-mathematica", в котором утверждал, что следующие шесть совершенных чисел должны соответствовать в формуле Евклида с такими значениями p: 17, 19, 31, 67, 127 и 257.

В то время проверить утверждение Мерсенна не представлялось возможным. Вычислить числа 2^p−1 с указанными значениями p было не так сложно, но требовалось ещё доказать, что они являются простыми. И как раз эта задача для математики того времени была неразрешима.

Позднее в записках итальянского профессора математики Катальди были обнаружены значения шестого и седьмого совершенных чисел: 8 589 869 056 и 137 438 691 328. Он обнаружил их в 1603 году. Эти числа как раз соответствовали предсказанным Мерсенном значениям p — 17 и 19. Но итальянец сделал это открытие за несколько десятков лет до француза. Однако и он упёрся в проблему простых чисел и не смог однозначно доказать свою правоту.

Позднее выяснилось, что Катальди действительно нашёл следующие два совершенных числа. Кстати, попутно он опроверг древнюю гипотезу о том, что все совершенные числа попеременно заканчиваются то на 6, то на 8.

Для историков науки до сих пор остаётся тайной, как именно Мерсенн и Катальди смогли открыть шестое и седьмое совершенные числа при тогдашнем уровне развития математики. Хотя сегодня мы знаем, что Мерсенн всё же допустил ошибку. Он правильно предсказал значения p = 31 и p = 127, но ошибся в значениях p = 67 и p = 257.

После этого в непростой истории совершенных чисел появилась ещё одна важная теорема. Леонард Эйлер доказал, что формула Евклида описывает все чётные совершенные числа. Про то, какими должны быть нечётные совершенные числа, и существуют ли они вообще, неизвестно до сих пор. Эйлер также доказал, что первые три значения p, которые предсказал Марен Мерсенн, действительно дают простые числа. Так семейство совершенных чисел пополнилось восьмым членом: 2 305 843 008 139 952 128 для p = 31.

Последний вычислительный подвиг и эпоха ЭВМ

Дальше процесс поиска совершенных чисел опять застопорился. Ведь учёным для этого требовалось доказывать простоту чисел, причём это приходилось делать путём обычных «ручных» вычислений. Мерсенн сам заявлял, что целой вечности не хватит для проверки простоты числа, которое имеет от 15 до 20 десятичных знаков.

Девятое совершенное число было найдено только в 1883 году. Честь этого открытия принадлежит пермскому сельскому священнику Ивану Михеевичу Первушину. Ему удалось вычислить самое большое для того времени простое число вида 2^p−1 для p = 61. Оно содержало 19 цифр: 2 305 843 009 213 693 951. Ему соответствовало совершенное число 2 658 455 991 569 831 744 654 692 615 953 842 176.

Больше таких вычислительных подвигов никто не совершал и следующие совершенные числа математики получили только в XX веке — с помощью появившихся счётных устройств. Десятое совершенное число (54 цифры) открыли в 1911 году, одиннадцатое (65 цифр) и двенадцатое (77 цифр) — в 1914 году.

Для поиска последующих совершенных чисел учёные уже использовали ЭВМ. В 1952 году американский математик Робинсон из Калифорнийского университета написал программу, которая сначала вычисляла значение очередного числа 2^p−1, а затем проверяла, является ли оно простым. С помощью этой программы 30 января 1952 года список совершенных чисел пополнился тринадцатым и четырнадцатым пунктами.

Загадки остаются, история продолжается

Сейчас известно чуть больше 50 совершенных чисел. Поиски продолжаются с привлечением всей мощи распределённых вычислений.

У совершенных чисел есть много интересных свойств. Например, все они — «треугольные». Это значит, что, взяв совершенное число шаров, мы всегда сможем сложить из них равносторонний треугольник.

Но самые главные тайны совершенных чисел пока не раскрыты. До сих пор никто не доказал, что количество совершенных чисел бесконечно. Кроме того, математиков очень занимает интересный вопрос: могут ли существовать нечётные совершенные числа. Ведь все известные на данный момент совершенные числа — чётные. Доказано, что если нечётное совершенное число существует, то оно должно быть больше 10¹⁵⁰⁰. Но обнаружить этого совершенного гиганта до сих пор не удалось, хотя для этого и организован специальный вычислительный проект.

Совершенные числа в «Симпсонах»

История совершенных чисел начиналась с мистической нумерологии пифагорейцев. Сейчас совершенные числа стали частью математического фольклора. Например, одно из них «засветилось» в культовом мультсериале «Симпсоны». В одной из серий, в которой Мардж и Гомер примеряют на себя профессию брачных консультантов, показано огромное табло на бейсбольном стадионе. Зрителям предлагается угадать, сколько человек посетило матч. На выбор предложены следующие варианты:

A) 8191
B) 8128
C) 8208
D) No way to tell.

Узнаёте число в варианте B? Это же четвёртое совершенное число! Кстати, первое и третье числа на табло тоже взяты не с потолка. Вариант A — это простое число Мерсенна. Так в математике называют простое число уже знакомого нам вида: 2^p−1. Число C  — это одно из «самовлюблённых чисел» (математики вообще любят давать числам задорные имена). Так называют число, которое равно сумме своих цифр, возведённых в степень, равную количеству этих цифр.

«Симпсоны» вообще славятся обилием математических отсылок и аллюзий. Дело в том, что многие сценаристы «Симпсонов» имеют математическое образование. В сериале частенько появляются примечательные математические шутки и загадки, которые интригуют зрителей. А совершенные числа по сей день продолжают оставаться звёздами на математическом небосводе. Поэтому их появление в сериале совсем не случайность.

Математика — удивительная наука. С одной стороны, она глубоко проникла в нашу повседневную жизнь. Практически всё, что нас окружает — от простейших бытовых предметов до сложной электронной техники — так или иначе связано с математикой. С другой стороны, математики порой занимаются какими-то «странными», с точки зрения стороннего наблюдателя, вещами. Например, веками ищут совершенные числа. Кому и какую пользу они могут принести? На это у математики всегда есть замечательный и универсальный ответ: бесполезных вычислений не бывает. Любое исследование рано или поздно может привести к важному открытию, о котором сейчас невозможно даже помыслить.

Что ещё почитать:

• Как Гомер Симпсон почти решил уравнение Великой теоремы Ферма

• Постоянная Капрекара. Феномен таинственного числа 6174