Авторы — Кынев С.М., Гончаров Р.К., Иванова А.Е., Самсонов Э.О
Научные сотрудники ООО «СМАРТС-Кванттелеком»
«Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».
Роберт Кавью
Случайные числа являются важнейшим ресурсом в большом числе практических приложений. Последовательности случайных чисел применяются в системах безопасности, криптографии (в том числе в квантовой криптографии), в научных исследованиях (статистике, моделировании различных систем и процессов), а также в играх.

Генераторы случайных чисел (ГСЧ) можно формально разделить на две категории: псевдослучайные и аппаратные. Генерация псевдослучайных чисел основана на математических алгоритмах, позволяющих получать каждое последующее число путем математического преобразования предыдущего числа согласно заданному алгоритму. Однако, зная предыдущие числа и математический алгоритм, можно предсказать всю последовательность. Алгоритмы генерации псевдослучайных чисел хорошо описаны в статье.
Аппаратные или физические ГСЧ, в свою очередь, можно разбить на две категории: классические и квантовые генераторы.
В классических ГСЧ источником энтропии служит процесс, который описывается законами классической физики. Детерминированность таких процессов дает потенциальную возможность злоумышленнику воспроизвести генерируемые классическим аппаратным ГСЧ последовательности. Квантовые генераторы случайных чисел (КГСЧ) в качестве физического источника энтропии используют квантовые процессы, которые сами по себе имеют вероятностную природу. Следовательно, КГСЧ может являться генератором истинно случайных числовых последовательностей, подходящих в том числе и для криптографических приложений.
Применение источников энтропии, построенных на основе эффектов квантовой
оптики, является одним из наиболее перспективных подходов к построению генераторов последовательностей недетерминированных случайных чисел, что
обеспечивается фундаментальной вероятностной природой квантовых процессов. На Хабре уже пытались собирать квантовый генератор случайных чисел. Вообще такие генераторы могут быть основаны на разных эффектах: регистрация фотонов в различных оптических модах, время обнаружения фотонов, счет фотонов в импульсе, фазовые шумы лазера, суперлюминесценция, рассеяние и т. д. Каждое такое устройство имеет как преимущества, так и недостатки.
В нашей компании мы разрабатываем квантовый генератор случайных чисел, основанный на флуктуациях вакуума (Рисунок 2).

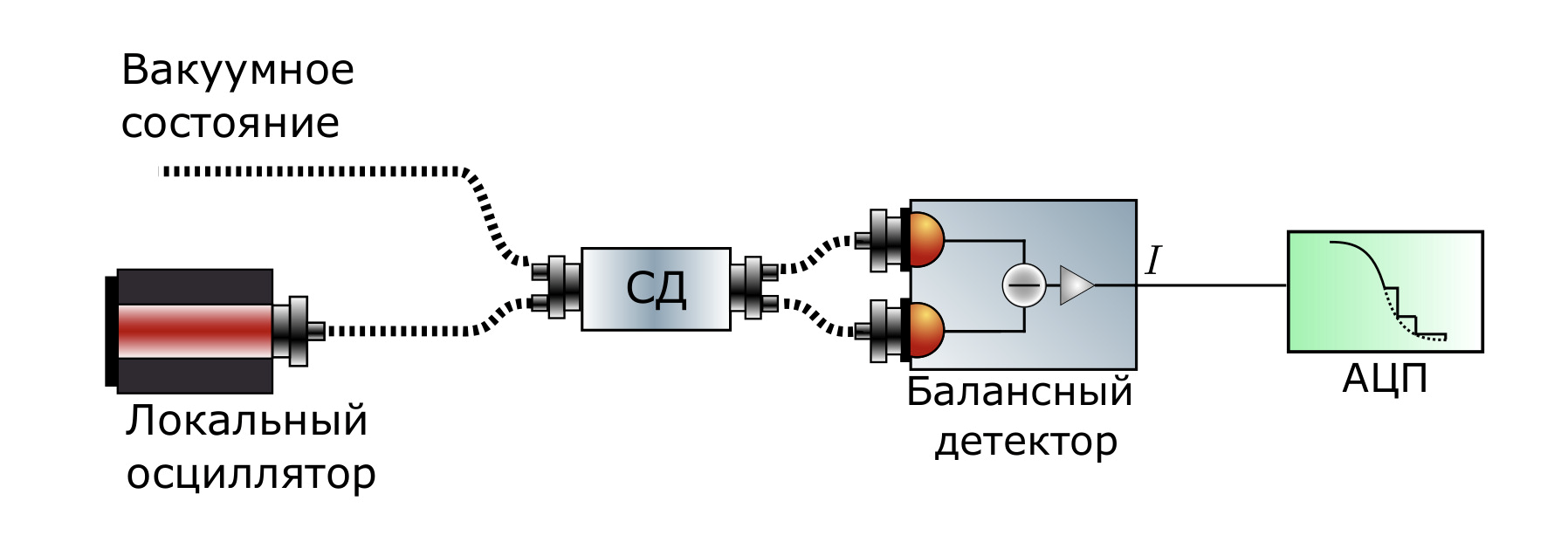
Принципом работы данного типа генераторов является извлечение случайности из квантового шума, получаемого после вычитания на балансном детекторе сигналов, полученных с выходов светоделителя (рисунок 3). На один из входов светоделителя при помощи локального осциллятора (лазера) подается когерентное состояние, а на второй — вакуум, на светоделителе (СД) эти сигналы смешиваются, а затем сигналы с его выходов поступают на балансный детектор (состоящий из фотодиодов с одинаковыми характеристиками и вычитающей схемы), где вычитаются друг из друга. Полученный при этом итоговый сигнал является квантовым шумом, который можно при помощи последующей обработки аналого-цифрового преобразователя (АЦП) превратить в случайную последовательность.
Максимальная случайность, которая может быть извлечена из последовательности, характеризуется минимальной энтропией (энтропия Реньи). Учитывая, что классическая составляющая шума может быть скомпрометирована, величина квантовой случайности характеризуется условной энтропией, которая учитывает возможность нарушителя использовать классический шум для управления генератором.
Энтропия Реньи с параметром а определяется выражением:

При a → 1 получаем случай энтропии Шеннона, при a → ∞ энтропия Реньи дает мин-энтропию, которая является наиболее консервативным способом оценки непредсказуемости:

С помощью мин-энтропии определяется количество равномерно распределенных бит, которые могут быть извлечены из конкретного распределения. При использовании такой оценки для практических устройств ГСЧ предполагается, что потенциальный нарушитель имеет максимальную вероятность угадать значение случайной величины.
Важным этапом работы любого физического генератора случайных чисел
является пост-обработка полученных экспериментально последовательностей. Блок постобработки получает на входе необработанную последовательность бит после АЦП и формирует из них более короткую последовательность, свободную от корреляций. Подобная операция называется экстракцией случайных бит. Экстракторы случайности — это функции (хэш-функции), которые преобразуют биты из необработанной последовательности в последовательность бит с сохранением части или всей случайности входной последовательности и имеющую распределение максимально близкое к равномерному. Существует большое количество экстракторов случайных бит. Компромисс выбора конкретной хэш-функции состоит в определении баланса между быстродействием и сохранением "случайности".
Одним из оптимальных экстракторов случайности является хэш-функция на основе матрицы Теплица, заключающееся в операции свертки исходной последовательности с некоторой последовательностью (ядром), состоящей из определенного конечного числа бит. Технически свертка реализуется умножением исходной последовательности на матрицу Теплица, составленную из выбранной последовательности бит. Размер матрицы определяется двумя параметрами: оценкой минимальной энтропии исходной последовательности и конечной требуемой скоростью генерации случайной последовательности бит.

Несмотря на то, что невозможно абсолютно точно оценить качество генерируемой случайной последовательности, есть методы обнаружения в ней корреляций, по которым можно отследить некорректную работу ГСЧ. Как правило, используются следующие наиболее известные батареи статистических тестов, которые применяются для оценки случайных последовательностей: DieHard и NIST. На хабре есть хорошая статья про то, как работают тесты NIST.
Таблица 1 – результаты прохождения статистических тестов NIST
№ |
Название теста |
Определяемый результат |
Результат |
|---|---|---|---|
1 |
Частотный тест |
Слишком много нулей или единиц |
Успешно |
2 |
Проверка кумулятивных сумм |
Слишком много нулей или единиц в начале последовательности |
Успешно |
3 |
Проверка «дырок» в подпоследовательностях |
Отклонение в распределении последовательностей единиц |
Успешно |
4 |
Проверка «дырок» |
Большое (малое) число подпоследовательностей нулей и единиц свидетельствует, что колебание потока бит слишком быстрое (медленное) |
Успешно |
5 |
Проверка рангов матриц |
Отклонение распределения рангов матриц от соответствующего распределения для истинно случайной последовательности, связанное с периодичностью последовательностей |
Успешно |
6 |
Спектральный тест |
Периодические свойства последовательности |
Успешно |
7 |
Проверка непересекающихся шаблонов |
Непериодические шаблоны встречаются слишком часто |
Успешно |
8 |
Проверка пересекающихся шаблонов |
Слишком часто встречаются m-битные последовательности единиц |
Успешно |
9 |
Универсальный статистический тест Маурера |
Сжимаемость (регулярность) последовательности |
Успешно |
10 |
Проверка случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определённого вида |
Успешно |
11 |
Разновидность проверки случайных отклонений |
Отклонение от распределения числа появлений подпоследовательностей определённого вида |
Успешно |
12 |
Проверка аппроксимированной энтропии |
Неравномерность распределения m-битных слов. Малые значения означают высокую повторяемость |
Успешно |
13 |
Проверка серий |
Неравномерность распределения m-битных слов |
Успешно |
14 |
Сжатие при помощи алгоритма Лемпела-Зива |
Большая сжимаемость, чем истинно случайная последовательность |
Успешно |
15 |
Линейная сложность |
Отклонение от распределения линейной сложности для конечной длины подстроки |
Успешно |
Для разработанного ФГСЧ, включающего в качестве основных компонент (Рисунок 3):
лазер c длиной волны 1550 нм и мощностью 5*10-3 Вт
балансный детектор с симметричным светоделителем,
АЦП 14 бит с частотой дискретизации 1 - 1.25 ГГц,
Мы получаем последовательность случайных чисел с минимальной энтропией 10-12 бит в зависимости от уровня шума входящих компонент. При этом, скорость генерации случайных чисел составляет порядка 500 Мбит/с. При этом батареи тестов будут успешно пройдены (Таблица 1).
Комментарии (23)

useribs
15.03.2024 08:55Вот только сегодня гуглил по доступным аппаратным устройствам. Какой же порядок стоимости данной разработки? 80Мбит/с источник стоит ~350USD (SwiftRNG Z).
И где может понадобиться источник хотя бы 10Мбит непрерывной рандомности

skynev
15.03.2024 08:55+1Понадобиться может, например, в системах квантовой рассылки ключей, о которых писали коллеги тут https://habr.com/ru/companies/quanttelecom/articles/778640/
Вас цена конечного устройства интересует или стоимость разработки?
useribs
15.03.2024 08:55Цена устройства по сравнению с конкурентами. Ну и в целом где нужны все эти сотни мегабит, в квантовой рассылке ключей (кстати видел, что европа запускает аж целые спутники QKDSat). Не просто же because they can было упомянуто что наше устройство выдает 500 Мбит

sci_nov
15.03.2024 08:55Интересно. Но непонятно что значит "смешиваются" на светоделителе? В итоге становится неясными дальнейшие операции вашего, как я понял запатентованного, устройства.
Есть мультипликативное смешивание (гетеродин, гомодин на смесителе), когда формируются суммарные и разностные частоты (в общем случае - комбинационные), а есть - аддитивное (сумматор). Светоделитель (насколько я понял из беглого анализа) сигнал из одного входа делит на два сигнала по параметру "мощность"... В общем, я в смятении).

Shkaff
15.03.2024 08:55Дело конечно хорошее! Любопытно, а на чем будете выезжать по сравнению с конкурентами (которых сейчас на том же принципе куча развелось, начиная с idquantique и пр.)? Или рынка хватит?

dprotopopov
15.03.2024 08:55в тему https://habr.com/ru/companies/serverspace/articles/770092/
В 1956 году министр финансов Великобритании Гарольд Макмиллан задумался о способах немного повысить благосостояние подданных Ее Королевского Величества, а заодно и пополнить государственную казну. Результатом его размышлений стало появление так называемых «премиальных облигаций». В отличие от обычных государственных ценных бумаг премиальные облигации не предлагали какого-либо фиксированного купонного дохода. Вместо этого их обладатели становились участниками ежемесячной лотереи, в которой разыгрывался процент по этим самым облигациям и множество денежных призов. Размер призов варьировался от 25 до 1 000 000 фунтов стерлингов, при этом полученные таким образом доходы не облагались налогами. Облигация могла принимать участие в ежемесячных розыгрышах спустя 30 дней после ее приобретения и вплоть до даты ее погашения, а государство обязалось выкупить эти ценные бумаги по номинальной цене по истечении срока их действия.

Премиальные облигации
Этот оригинальный инвестиционный инструмент был торжественно представлен на Лондонской бирже 1 ноября 1956 года, и самую первую премиальную облигацию приобрел у генерального почтмейстера доктора Чарльза Хилла лорд-мэр Лондона сэр Катберт Экройд, обогатив бюджет Великобритании на 1 фунт стерлингов. Новинка очень понравилась жителям туманного Альбиона, и вскоре премиальные облигации стали пользоваться неизменным спросом. К концу 1956 года было продано около 50 миллионов облигаций, каждая из которых имела уникальный серийный номер. На сегодняшний день такими ценными бумагами владеют более 24 миллионов англичан.
В ходе лотерей, где определялись счастливчики, требовалось случайным образом выбирать большое количество серийных номеров выигравших облигаций, причем таким образом, чтобы ни у кого не возникло даже малейших сомнений в беспристрастности алгоритма. Все-таки речь шла о миллионах фунтов стерлингов. Иными словами, простых лототронов с пронумерованными шариками тут оказалось явно недостаточно. И британское правительство решило построить для этих целей специальный Лотерейный Компьютер, который эффективно решал бы столь непростую задачу. Тут-то чиновники и вспомнили про талантливого инженера Томаса Флауэрса, считавшегося одним из самых продвинутых компьютерщиков Англии в 1956 году. Тем более, ранее он уже успешно работал на британское правительство, и не просто на правительство, а на Министерство обороны и военную разведку.

alcotel
15.03.2024 08:55+1Я вот не понял: какие преимущества имеет Ваша схема генератора шума с оптикой? Или, например, те же схемы с детектированием ядерного распада?
Непосредственное использование чисто электронного дробового или теплового шума ведь в разы проще. И этот способ тоже вполне можно назвать квантовым из-за дискретности заряда. И скомпрометировать источник шума, если он внутри прибора, также не получается.
Если в схеме выключить лазер, и просто усилить собственный шум одного фотодетектора, изменится ли результат?

sci_nov
15.03.2024 08:55Мне кажется, что пока мы не поймем что такое светоделитель и вакуумное состояние - бесполезно делать какие-либо выводы.
А так да, можно, например, оцифровать собственный шум радара. Но не думаю, что он будет квантовым, так как зарядов, формирующих шум, много, то есть это макроскопическое проявление электронов. Из-за неидеальной частотной характеристики аппаратуры придется делать цифровое выравнивание АЧХ и некоторые другие приёмы из-за фазовых шумов, например. В целом, собственный шум будет иметь гауссовское распределение, поэтому придется делать доп. обработку для получения равномерного распределения. Возможно, аппарат из данной статьи сразу даёт равномерное распределение)


j_aleks
....."На один из входов светоделителя при помощи локального осциллятора (лазера) подается когерентное состояние, а на второй — вакуум"....
что значит ..."подается вакуум"... , как то звучит метафизически...
Oangai
Да ладно, главное что у прибора вход для этого предусмотрен, покупателю всего-то нужно провести волновод в космос по своему усмотрению, в идеале подключиться к центру галактики...
Radisto
Может там жидкий вакуум? Немножко в баночке
sim2q
https://ru.wikipedia.org/wiki/Гигантский_войд
hyperon1
Это жаргонное слово для вакуумного состояния оптического поля, если вы знакомы с фоковским базисом, то это будет |0>. Это означает что в оптическим поле нет фотонов.
Oangai
вопрос был скорее где его взять, какие бывают для этого решения, как оно работает. Технически это действительно интересно, а в статье никак не раскрыто.
Toloroloe
Рассматривая оптическую схему, можно закрыть один из входных портов светоделителя. Когерентное детектирование и в квантовой оптике используется для регистрации ослабленного излучения (например, когерентного состояния) с помощью опорного сигнала, который даёт усиление на вычитающей схеме детектора. Существует неопределённость в результате измерения по амлитуде и фазе. Здесь же ослабленное излучение отсутствует (порт закрыт), но вакуумные флуктуации (неопределённость) при этом никуда не исчезают и служат источником случайности.
hyperon1
Сейчас задумался о том, что это по сути ведь не вакуумные флуктуации. Так как опорный сигнал это когерентное состояние, то после того как мы разбиваем его на два сигнала делителем пучка, измеряется разница числа зарегистрированных фотонов в этих сигналах. Получается что классический сигнал является источником энтропии
Toloroloe
Именно источником энтропии являются вакуумные флуктуации. Разница по сути содержит неопределённость, неизбежно возникающую в результате измерения.
hyperon1
Если мы подадим два классических сигнала с одинаковой мощностью на сбалансированный фотодиод, то тогда выход получится такой же как и для ситуации описанной в статье, так как за рандомность отвечает дробовой шум
Shkaff
Так дробовой шум берется как раз из квантового шума лазера.
hyperon1
Я согласен, просто мне пришло озарение, что по сути никаких вакуумных флуктуаций не измеряется Так как опорный сигнал является когерентным состоянием, то в нем также неопределено число фотонов, что и вызывает дробовой шум. В такой схеме измеряется дисперсия числа фотонов в опроном сигнале. Иными словами источником энтропии является квантово-оптические флуктуации классического сигнала. Вещь очевидная, просто я никогда об этом не задумывался с такого ракурса (другой это то, что измеряются квадратуры вакуума)
Shkaff
Не совсем: в данном случае измеряется именно вакуум, это следует чисто из процедуры измерения (разностная схема). Если бы вы измеряли поле опорного сигнала до делителя луча, вы бы измеряли квантовые флуктуации этого опорного луча, а когда измеряете после — измеряете смесь флуктуаций опорного луча и вакуума, а в разностной схеме остаются только флуктуации вакуума.
Это может казаться несущественным, но если заменить вакуум на сжатый вакуум, например, то мы будем измерять именно эту статистику, а не флуктуации накачки. Я именно с этим работаю в научной жизни (вот тут на хабре один из примеров описывал).
Подробнее через математику
Давайте обозначим вакуумное поле на входе светоделителя как v, а когерентную накачку — как сумму классической амплитуды L и квантовых флуктуаций l. Тогда на выходах светоделителя будет:
Это амплитуды поля, а измеряются интенсивности:
А потом берется их разность:
Члены lv — второго порядка малости, их можно отбросить. Остаются только члены пропорциональные когерентной амплитуде. И эти члены содержат только вакуумные флуктуации!
hyperon1
В случае сжатого вакуума понятно, что не подойдёт то, что я описал ранее, тк в сжатом вакууме фотоны присутствуют и там оператор не тривиальный.
В случае когда смешивается когерентное состояние с обычным вакуумом, это будет эквивалентно случаю если бы на фотодиоды подали бы два сигнала с одинаковой мощностью и одинаковой центральной частотой. И никакого вакуума в таком случае нет. В общем только в этом частном случае, такое измерение можно трактовать по-разному. Или я ещё что-то упустил?
Shkaff
Можно было бы сделать наоборот: сжать состояние опорного луча. В таком случае вы бы наблюдали ровно вакуум, а не сжатое состояние. Ну или взять тепловое состояние для опорного луча. Вне зависимости от его температуры вы все равно будете наблюдать вакуумные флуктуации.
Если взять случай чисто когерентного состояния, то просто смотря на статистику различить случай, когда вы посылаете два отдельных пучка на два фотодиода или делите один пополам, нельзя.
Собственно выше описана причина, почему не используют один лазер: помимо квантового шума там классические шумы, и вот они разрушают получение истинно случайных чисел. Разностная схема позволяет измерять вакуум, тем самым избегая влияния любых шумов лазера.