Принято считать, что две базовые операции «машинного обучения» — это регрессия и классификация. Регрессия — это не только инструмент для выявления параметров зависимости y(x) между рядами данных x и y (чему я уже посвятил несколько статей), но и частный случай техники их сглаживания. В этом примере мы пойдем чуть дальше и рассмотрим, как можно проводить сглаживание, когда вид зависимости y(x) заранее неизвестен, а также, как можно отфильтровать данные, которые контролируются разными эффектами с существенно разными временными характеристиками.

Один из самых популярных алгоритмов сглаживания, применяемый, в частности, в биржевой торговле — это скользящее усреднение (включаю его в цикл статей по машинному обучению с некоторой натяжкой). Рассмотрим скользящее усреднение на примере колебаний курса доллара на протяжении нескольких последних недель (опять-таки в качестве инструмента исследования используя Mathcad). Сами расчеты лежат здесь.




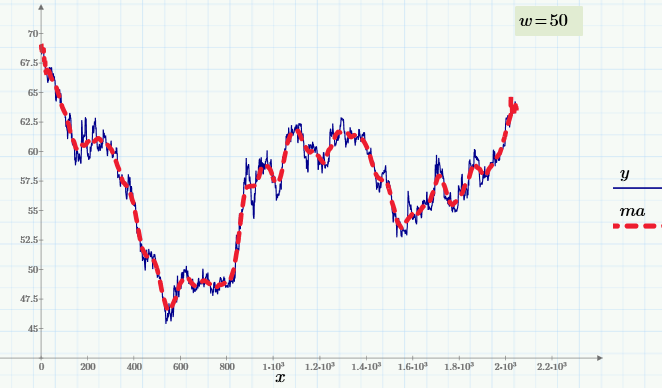
Приведенный график демонстрирует биржевое значение курса доллара к рублю с интервалом в 1 час. Исходные данные представлены синей кривой, а сглаженные — красной. Даже невооруженным глазом видно, что колебания курса имеют несколько характерных частот, что и является предметом одного из направлений технического анализа рынков.

Сглаживание при помощи «скользящего среднего»
Принцип сглаживания на основе «скользящего среднего» (МА — от англ. «moving average») состоит в расчете для каждого значения аргумента y_i среднего значения по соседним w данным.



Число w называют окном скользящего усреднения: чем оно больше, тем больше данных участвуют в расчете среднего, соответственно, тем более гладкая кривая получается. На верхнем рисунке окно w=50, а вот как будет выглядеть скользящее усреднение при w=200.



Как меняется Фурье-спектр данных при скользящем усреднении?
Очевидно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций. Это типичный пример фильтрации данных, т.е. устранения одной из составляющих зависимости y(x_i). Наиболее часто целью фильтрации является подавление быстрых вариаций y(x_i), которые обычно обусловлены шумом. В результате из быстроосциллирующей зависимости y(x_i) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.

Эти рассуждения плавно перевели нас к терминологии спектров. Давайте нарисуем график Фурье-преобразования («Фурье-спектр») исходных данных:



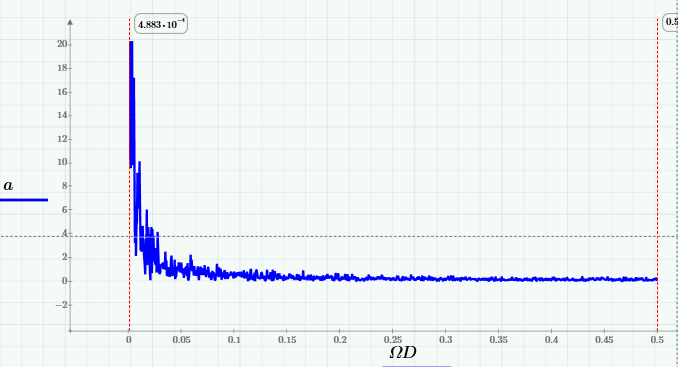
и убедимся в том, что спектр скользящего среднего вырезает из него высокие частоты (начиная примерно с частоты 0.005 Гц):



Пояснение: Фурье-спектр суммы синусов и ее МА
Для того чтобы пояснить принцип расчета Фурье-спектра, рассмотрим вместо (случайных) исходных данных простую модель суммы нескольких детерминированных сигналов (синусоид с разной частотой и амплитудой) и псевдослучайного шума:



Приведем графики этой суммы и ее МА (с тем же окном w=200):



а также их Фурье-спектры:



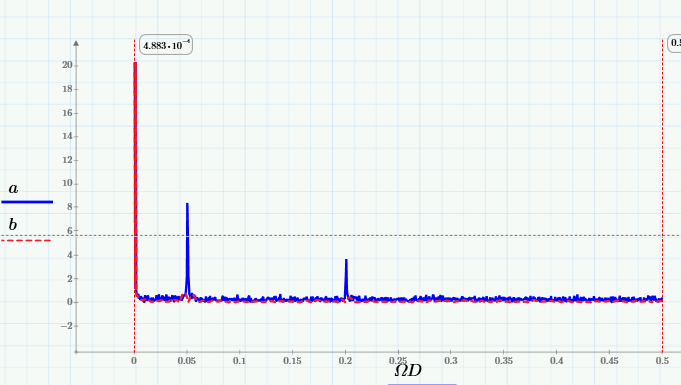
Из них видно, что скользящее усреднение вырезает из сигнала высокие частоты, начиная с частоты 0.005 Гц. Лучше это видно на крупном плане низкочастотной области спектра:



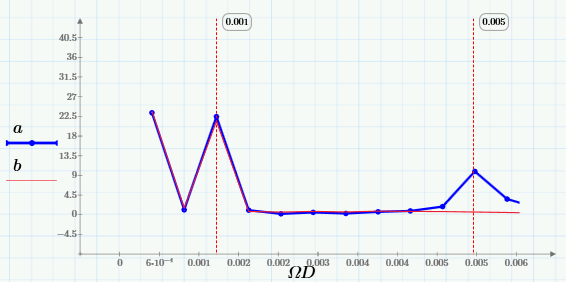
Таким образом, выбирая подходящее окно, можно сдвигать область подавляемых частот в нужную сторону (чем больше w, тем дальше эта граница сдвигается влево).

Полосовая фильтрация
Вернемся к биржевой аналитике и продемонстрируем исключительно простой способ вырезания из исходных данных нужной полосы частот. А именно, в противоположность подавления шума (высокочастотной составляющей) часто рассматривают и противоположную задачу — устранение медленно меняющихся вариаций (иногда эту задачу называют устранением тренда, или детрендингом). При помощи скользящего усреднения ее реализовать очень просто — путем вычитания из сигнала МА (с подобранным окном):



Также интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением «полосовой фильтрации», которая реализуется так:
1. Устранение из сигнала y высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например, с помощью скользящего усреднения с малым окном (например, w=200).
2. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w.
3. Вычитание из сигнала middle тренд slow, тем самым выделяя среднемасштабную составляющую исходного сигнала y.

Оставляю заинтересовавшемуся читателю возможность самому реализовать полосовую фильтрацию в Mathcad Express (с небольшой оговоркой, что в бесплатной версии Маткада алгоритм БПФ расчета Фурье-спектров отключен, и с ним поиграться не получится). Сами расчеты находятся здесь.

Литература:
1. Кирьянов Д.В., Кирьянова Е.Н. Вычислительная физика (PDF, гл.1, п.6 и 7). М.: Полибук Мультимедиа, 2006.
2. Бат М. Спектральный анализ в геофизике. М., Наука, 1980.