Об энтропии говорят всякое: энтропия увеличивается со временем, энтропия — это беспорядок, энтропия увеличивается с ростом энергии, энтропия определяет стрелу времени и т. д.. Но я понятия не имел, что такое энтропия, и, судя по тому, что я обнаружил, большинство других людей тоже. Вот вам объяснение, которое я и сам хотел бы получить, когда мне впервые рассказали об энтропии, так что, надеюсь, вы найдёте его полезным. Моя цель состоит в том, чтобы к концу этого длинного поста у нас было строгое и интуитивное понимание этих утверждений, и в частности того, почему Вселенная выглядит по-разному при движении вперёд во времени и при движении назад во времени.

Это путешествие начинается с определения и понимания энтропии. Существует множество формальных определений энтропии в разных дисциплинах — термодинамика, статистическая механика, теория информации, — но всех их объединяет одна главная идея: энтропия количественно выражает неопределённость. Проще всего познакомиться с энтропией через теорию информации, которая приведёт к энтропии в физических системах, а затем к взаимосвязи между энтропией и временем.

Теория информации

Представьте, что вы хотите сообщить своему другу результат какого-то случайного события, например, результат броска костей или номера, выпавшие в лотерее, но при этом вы хотите сделать это с помощью наименьшего возможного количества битов (только 1 и 0). Во сколько битов вы сможете уложиться?

Создатель теории информации Клод Шеннон пытался ответить на подобные вопросы во время своей работы в лаборатории Bell Labs. Он разрабатывал математические основы связи и сжатия информации, и в конце концов обнаружил, что минимальное количество битов, необходимое для передачи сообщения, напрямую связано с неопределённостью сообщения. Затем он смог сформулировать уравнение для количественной оценки неопределённости сообщения. Когда он поделился этим уравнением со своим коллегой-физиком из Bell Labs Джоном фон Нейманом, фон Нейман предложил назвать его энтропией по двум причинам:

Фон Нейман, как сообщает Шеннон, предположил, что есть две веские причины называть функцию «энтропией». «Её уже так называют, — сказал он, — и, кроме того, это даст вам большое преимущество в спорах, потому что никто не знает, что такое энтропия». Шеннон назвал эту функцию «энтропией» и использовал её как меру «неопределённости», без всякой дискриминации чередуя эти два слова в своих работах.

• Гарольд А. Джонсон (ред.), Теплопередача, термодинамика и образование: Boelter Anniversary Volume (New York: McGraw-Hill, 1964), p. 354.

Позже мы увидим, что связь между энтропией Шеннона и существовавшим до него определением энтропии была не просто случайной, а прочной и глубокой.

Но теперь давайте посмотрим, как Шеннон нашёл определения для таких обычно расплывчатых терминов, как «информация» и «неопределённость».

В теории информации информация о наблюдаемом состоянии формально определяется как количество битов, необходимых для передачи этого состояния (по крайней мере, для системы с равновероятными исходами во второй степени, но вскоре мы увидим, как это обобщить). Вот несколько примеров информации:

• Если я подброшу обычную монету, то для того, чтобы сообщить вам результат её падения, потребуется один бит информации: 0 для орла и 1 для решки.

• Если я брошу честную 8-гранную игральную кость, я смогу представить результат с помощью 3 битов: 000 для 1, 001 для 2, 010 для 3 и т. д.

Чем больше исходов может быть у системы, тем больше битов (информации) потребуется для обозначения результата. Если система имеет N равновероятных исходов, то для представления результата потребуется бит информации.

Энтропия определяется как ожидаемое количество битов информации, необходимое для представления состояния системы (это на самом деле ложь, но на данный момент это определение будет полезным для нас — мы исправим его позже). Таким образом, энтропия монеты равна 1, поскольку в среднем мы ожидаем, что для представления исхода монеты потребуется 1 бит информации. Энтропия 8-гранной игральной кости равна 3 битам, поскольку мы ожидаем, что для представления результата потребуется в среднем 3 бита.

Изначально кажется, что энтропия — ненужное определение, поскольку мы можем просто посмотреть, сколько битов требуется для представления результата нашей системы, и использовать это значение; но это верно только в том случае, если вероятность исходов одинакова.

Представьте, что у меня есть шулерская 8-гранная игральная кость, на которой число 7 выпадает в 50% случаев, а остальные грани выпадают в ~ 7,14% случаев. Теперь, если мы достаточно умны, мы сможем уменьшить ожидаемое количество битов, необходимых для передачи результата игры в кости. Мы можем решить, что 7 будет обозначаться 0, а все остальные числа будут обозначаться 1XXX, где иксы — это некоторые уникальные биты. Это будет означать, что в 50% случаев для представления результата нам потребуется только 1 бит информации, а в остальных 50% случаев мы используем 4 бита, поэтому ожидаемое количество битов (энтропия игральной кости) равно 2,5. Это меньше, чем энтропия в 3 бита для честной 8-гранной игральной кости.

К счастью, нам не нужно придумывать хитроумную схему кодирования для всех возможных систем — существует закономерность в том, сколько битов информации требуется для представления состояния с вероятностью p. Мы знаем, что если, например, p = 0,5, то есть монета упала решкой, то для представления такого исхода требуется 1 бит информации. Если, например, p = 0,5, к примеру, когда на 8-гранной игральной кости выпало число 5, то для представления этого исхода требуется 3 бита информации. Если же вероятность выпадения 7 на нашей шулерской 8-гранной кости p = 0,5, то, как и в случае с монетой, требуется 1 бит информации, что показывает нам, что на самом деле имеет значение лишь вероятность исхода. Таким образом, мы можем найти уравнение для количества битов информации, необходимых для состояния с вероятностью p.

Эту величину I обычно называют информативностью или неожиданностью, поскольку чем меньше вероятность появления состояния, тем больше неожиданность, когда оно вдруг наступает.

Когда вероятность мала, неожиданность велика, а когда вероятность велика, неожиданность мала. Это более общая формула, чем «количество необходимых битов», поскольку она позволяет состояниям, вероятность которых исключительно высока (например, 99% вероятности) иметь удивление меньше 1, что более осмысленно, чем если бы мы пытались интерпретировать это значение как «количество битов, необходимых для представления исхода».

И теперь мы можем исправить наше определение энтропии (ложь, которую я сказал ранее). Энтропия — это не обязательно ожидаемое количество битов, используемых для представления системы (хотя это так, если вы используете оптимальную схему кодирования), но в более общем случае энтропия — это ожидаемая неожиданность системы.

И теперь мы можем вычислить энтропию таких систем, как игральная кость или монета, или любой другой системы с известными вероятностями исходов. Ожидаемая неожиданность (энтропия) системы с N возможных исходов, каждый из которых имеет вероятность p_i (все они складываются в 1), можно вычислить как:

энтропия Шеннона

Заметим, что если все вероятности N одинаковы (так, что ), то уравнение энтропии может упроститься до

Вот несколько базовых примеров с использованием энтропии Шеннона.

Энтропия честной монеты равна:

Энтропия честной 8-гранной игральной кости равна:

Энтропия шулерской 8-гранной игральной кости, в которой игральная кость выпадает одной гранью 99% времени, а другими гранями остальные 1% времени с равной вероятностью между ними (около 0,14% каждая), составляет:

Надеюсь, теперь вам стало немного понятнее, что энтропия представляет собой неопределённость. Энтропия 8-гранной игральной кости будет выше, чем у монеты, поскольку у нас существует большая неопределённость в отношении результата броска 8-гранной игральной кости, чем в отношении монеты (8 равновероятных исходов более неопределённы, чем только 2 равновероятных исхода). Но крайне несправедливая 8-гранная игральная кость имеет меньшую энтропию, чем даже монета, так как у нас очень высокая степень уверенности в исходе несправедливой игры в кости. Теперь у нас есть уравнение для количественной оценки неопределённости (энтропии) системы.

Сейчас не совсем понятно, какое отношение это определение энтропии имеет к беспорядку, теплу или времени, но идея энтропии как неопределённости является фундаментальной для понимания энтропии Вселенной, которую мы рассмотрим в ближайшее время. Для справки, это определение энтропии называется энтропией Шеннона.

Сейчас мы пойдём дальше, но я рекомендую более подробно изучить теорию информации. Она имеет множество важных прямых следствий для сжатия данных, исправления ошибок, криптографии и даже лингвистики, а также затрагивает практически все области, связанные с неопределённостью, сигналами или знаниями.

Физическая энтропия

Теперь мы посмотрим на энтропию под совершенно другим углом зрения — со стороны статистической механики. Начнём с проверенного и верного введения в энтропию, которое даётся каждому студенту.

Шары в коробке

Я дам вам коробку с 10 шариками в ней, от p₀ до p₉, и мы посчитаем, сколько шаров находится в левой части коробки и в правой. Предположим, что каждый шарик с равной вероятностью окажется на любой стороне. Сразу же видно, что маловероятно, что все шары окажутся на левой стороне коробки, и более вероятно, что мы увидим равное количество шаров на каждой из сторон. Почему так?

Ну, есть только одно состояние, в котором мы увидим все шары слева — если каждый шар будет слева (это, конечно, удивительный факт – но прошу вас оставаться со мной). Но существует множество способов, с помощью которых коробку можно сбалансировать. Мы могли бы переместить шары от p₀ до p₄ на одну сторону, а остальные — на другую, или же сделать наоборот, зеркально, или поместить все чётные шары на одну сторону, а нечётные — на другую, или наоборот, или составить любую другую из множества возможных комбинаций.

Эта коробка — система, энтропию которой мы можем измерить, по крайней мере, после того, как я скажу вам, сколько шаров находится на каждой стороне. На осознание этого может потребоваться некоторое время, но представьте коробку с нашими количествами шаров слева и справа как систему, где результатом будет описание того, где находятся все отдельные шары в коробке. Это напоминает бросание игральной кости и наблюдение за тем, какой гранью она упадёт.

Это означает, что для системы-коробки, где мы видим все шары слева, возможен только один исход: все шары находятся слева. Это означает, что данная система обладает нулевой энтропией (отсутствие ожидаемого сюрприза), поскольку мы уже знаем, где найдём каждый отдельный шарик.

У коробки со сбалансированным количеством шаров (по 5 на каждой стороне) есть множество возможных равновероятных исходов, и, по сути, мы можем их сосчитать. Знаменитое уравнение в комбинаторике — это уравнение «число сочетаний из N по k», которое рассчитывает именно такой сценарий. Оно говорит нам, что существует 252 возможных способа, которыми мы можем разместить по 5 шаров с каждой стороны. Тогда энтропия этой системы будет равна . Это то же самое, что вычислить энтропию 252-гранной игральной кости.

А если мы увеличим количество шаров, то энтропия сбалансированной коробки возрастёт, так как в этом случае будет ещё больше возможных комбинаций, которые могут составить сбалансированную коробку.

Мы должны интерпретировать эти результаты следующим образом: чем больше у нас способов соответствовать масштабным измерениям (подсчёту количества шаров на каждой стороне), тем выше энтропия системы. Когда все шары находятся слева, существует только один способ соответствовать этому измерению, поэтому энтропия системы низка. Когда существует множество способов уравновесить её с обеих сторон, энтропия высока.

Здесь мы видим 1000 мячей, прыгающих в коробке. Все они стартуют слева, поэтому энтропия коробки равна 0, но как только шарики начнут переходить вправо и изменять количество с каждой стороны, энтропия возрастёт.

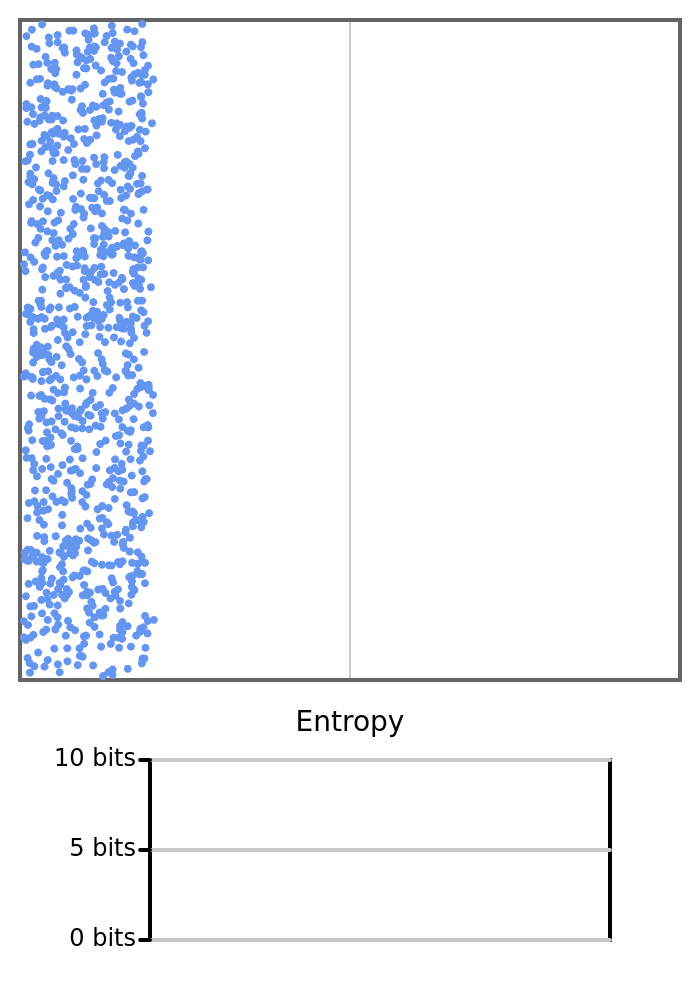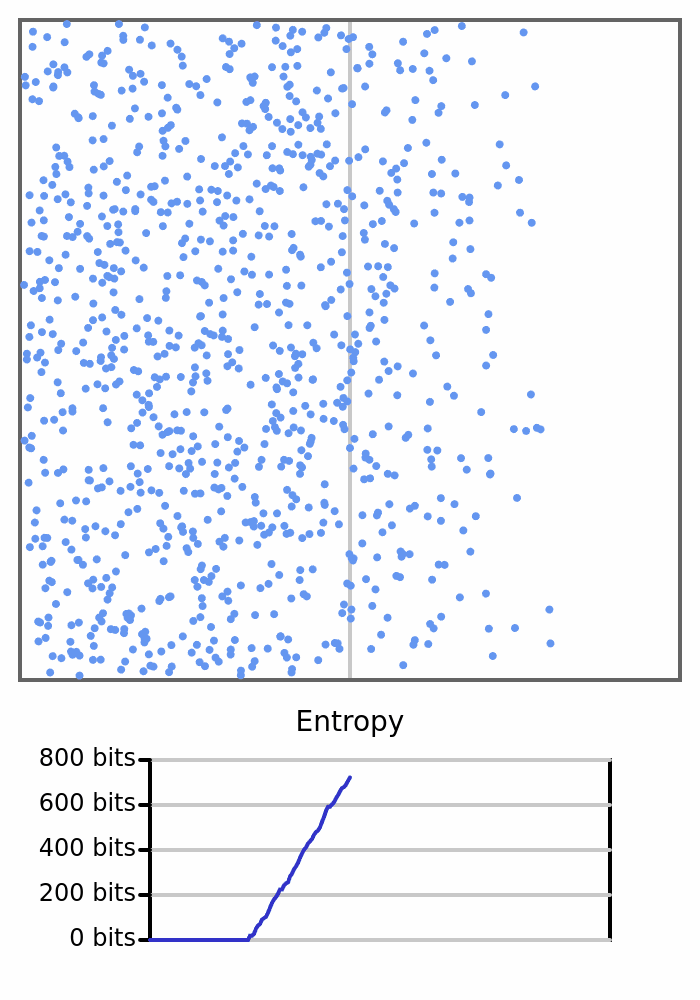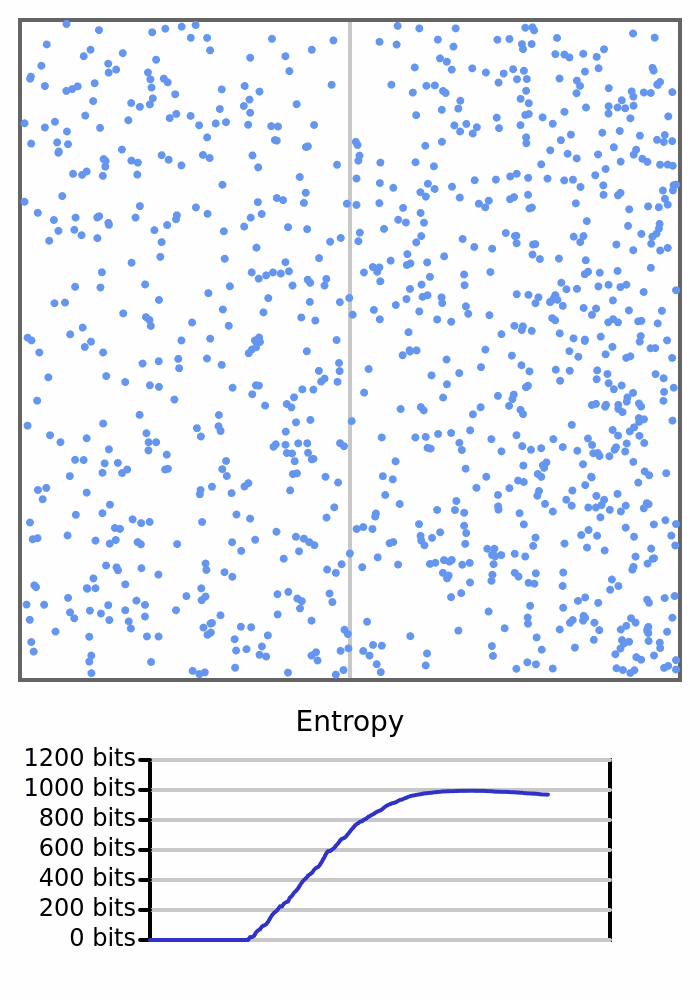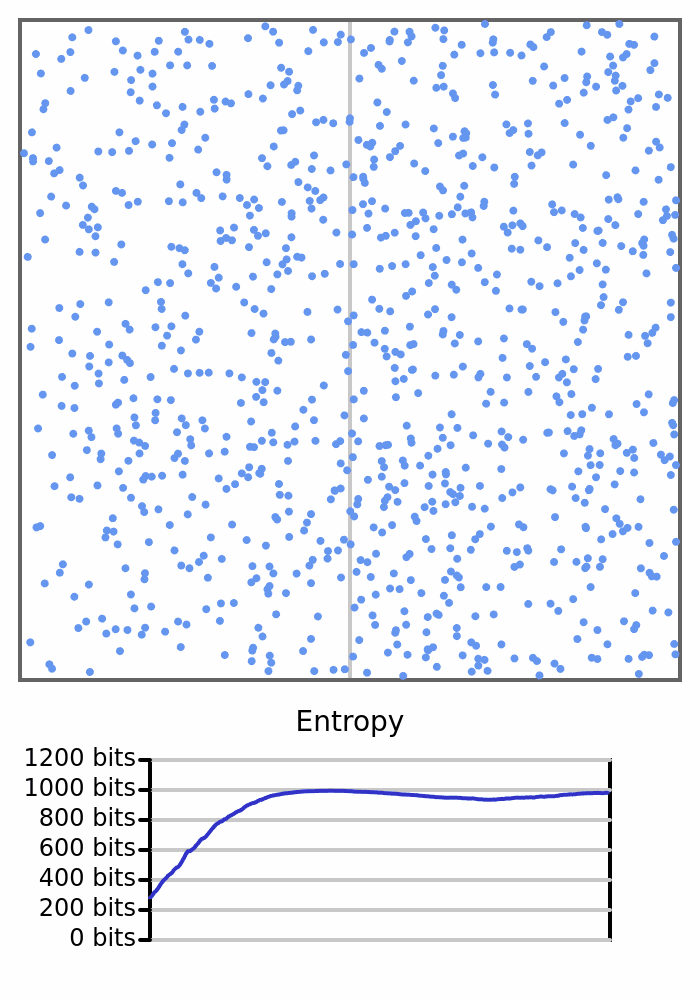
В статистической механике формальный термин для крупномасштабного измерения — макросостояние, а конкретные состояния, которые могут удовлетворять этому измерению, — микросостояния. Измерение количества шаров на каждой стороне коробки мы бы назвали макросостоянием, а различные комбинации положений отдельных шаров — микросостояниями. Перефразируя вышесказанное: существует только одно микросостояние, соответствующее макросостоянию, в котором все шары находятся на одной стороне, и множество микросостояний, соответствующих макросостоянию сбалансированной коробки.

Но почему мы решили измерить количество шаров слева и справа? Мы могли бы измерить другое макросостояние, и энтропия была бы другой.

Макросостояния

Представьте, что вместо того, чтобы выбирать левую и правую половину коробки для подсчёта количества шариков, мы вместо этого считаем, сколько шариков находится в каждом пикселе коробки. В этом случае энтропия почти всегда будет максимальной, поскольку шарики редко делят один пиксель. Даже если бы все шары находились в левой части коробки, они, скорее всего, занимали бы каждый свой пиксель, и измеренная энтропия была бы такой же, как если бы шары были равномерно распределены в коробке.

Если мы применим дорогой прибор для измерения коробки и отслеживания шаров с высокой точностью, то энтропия будет меняться редко и будет очень высокой. Если же мы используем недорогой прибор, который может определить только, находится ли шарик слева или справа от коробки, то энтропия будет низкой и может легко колебаться, если некоторые шарики временно окажутся на одной стороне коробки.

Давайте снова запустим точно такую же симуляцию 1000 шаров в коробке, по-прежнему начиная с шаров слева. Но на этот раз мы посчитаем, сколько шариков находится в каждой ячейке сетки 50x50, а не просто в одной из двух ячеек (левой или правой). Энтропия будет высокой, поскольку существует множество микросостояний, обозначающих кучу ячеек, в которых находится только один шарик, и энтропия не сильно изменится, поскольку два шарика редко делят одну и ту же ячейку. Вспомните, что если два шара делят одну и ту же ячейку, то их количество увеличивается, и существует меньше микросостояний, удовлетворяющих ячейке с количеством 2, чем двум ячейкам с количеством 1 в каждой.

Энтропия присуща не только физической системе, но и нашему описанию её — т. е. макросостоянию, которое мы измеряем, и разрешению, с которым мы его наблюдаем.

Этот процесс измерения версии нашей системы с более низким разрешением (например, подсчёт количества шариков в левой или правой части коробки) называется грубозернистым.

То, как мы выбираем/измеряем макросостояние, то есть то, как мы «огрубляем» систему, зависит от проблемы, которую мы решаем.

• Представьте, что у вас есть коробка с газом (как наши шарики в коробке, но в масштабах 10²⁵ шариков в коробке), и мы помещаем считыватель температуры на левую и правую стороны коробки. Это даст нам макросостояние, состоящее из двух отсчётов средней скорости шариков на левой и правой сторонах коробки. Затем мы можем вычислить энтропию, сравнивая состояния, когда показания термодатчиков равны, с состояниями, когда они отличаются на T градусов. Когда мы узнаем, как взаимодействуют время и энтропия, мы будем использовать эту модель, чтобы показать, что два термодатчика должны со временем сходиться к одному и тому же значению.

• Представьте, что вы проводите секвенирование генома многих людей в популяции, и вы можете выбрать множество различных макросостояний в зависимости от того, что вас интересует. Вы можете подсчитать, сколько каждого нуклеотида содержится во всех последовательностях, что позволит вам количественно оценить, насколько изменчивы четыре нуклеотида в ДНК. Можно рассчитать энтропию каждой отдельной позиции в последовательности ДНК, подсчитав, сколько типов нуклеотидов используется в этой позиции в популяции, что позволит вам определить участки ДНК, которые постоянны у разных людей или различаются у разных людей.

Выбор способа измерения макросостояния может быть различным для одной и той же системы, в зависимости от того, что вы можете измерить и/или что вам важно измерить.

Но как только у нас есть макросостояние, нам нужен способ определить все микросостояния и присвоить им вероятности.

Микросостояния

Когда мы рассматривали расположение шариков в коробке в одинаковых по размеру ячейках, было легко заметить, что каждый шарик с одинаковой вероятностью может оказаться в любой из ячеек, поэтому каждое микросостояние было одинаково вероятным. Это очень упростило расчёт энтропии, мы просто использовали упрощённую версию энтропии Шеннона, чтобы найти, что для W микросостояний, удовлетворяющих заданному макросостоянию, энтропия системы равна . Нетрудно распространить эту идею на микросостояния, которые не являются равновероятными.

Например, рассчитаем энтропию коробки с 5 шариками слева и 5 шариками справа, но заменим один из шариков в коробке металлическим шариком, который притягивается магнитом влево. В этом случае вероятность каждого микросостояния уже не будет одинаковой. Если мы предположим, что существует 80% вероятность того, что металлический шарик окажется слева, а не справа, то энтропию коробки можно рассчитать следующим образом: для всех 252 микросостояний в 126 из них металлический шар находится слева, и шансы этого составляют 0,8, а в остальных 126 — справа, и шансы этого составляют 0,2. Это означает, что с помощью формулы для энтропии Шеннона мы получим энтропию

Это немного меньше, чем у коробки с обычными шариками, энтропия которой составляла 7.9772799235. Именно этого и следовало ожидать: мы немного более уверены в исходе этой системы, поскольку знаем, где с большей вероятностью окажется один из шаров.

Но тут возникает тонкий вопрос: почему мы выбрали именно этот набор микросостояний? Например, если у нас есть макросостояние из 5 шаров слева и 5 шаров справа, но мы решили использовать сетку 50x50 ячеек для описания микросостояний, то микросостояний, удовлетворяющих макросостоянию, будет гораздо больше, чем если бы мы использовали сетку 2x1 – с ячейкой слева и ячейкой справа.

Давайте рассчитаем энтропию для этих двух примеров. Не забывайте, что у них одинаковое макросостояние: 5 шаров слева и 5 шаров справа.

• Если мы воспользуемся микросостоянием и посмотрим на распределение отдельных шариков между двумя ячейками, делящими коробку пополам, то с помощью «числа сочетаний из N по k» вычислим, что существует 252 возможных комбинации распределения шариков между двумя ячейками. Это даёт нам энтропию $ \text{log}_2(252) = 7.977279923 $.

• Если мы решили использовать микросостояния, рассматривая положение отдельных шаров относительно 50x50 (2500) ячеек, делящих коробку на сетку, то мы можем использовать «числа сочетаний из N по k», чтобы вычислить, что существует 252 возможных комбинации распределения шаров между двумя половинами коробки, для каждой из которых каждый шар может оказаться в любой из 50x25 (1250) ячеек. Это даёт нам энтропию .

Этот результат очень хорошо согласуется с нашим информационно-теоретическим пониманием энтропии: когда мы позволяем большему количеству микросостояний представлять одно и то же макросостояние, мы становимся более неопределёнными относительно того, в каком микросостоянии находится наша система. Однако этот результат вызывает некоторые опасения.

Если разные микросостояния дают разную энтропию, как нам выбрать правильные микросостояния для нашей задачи? В отличие от макросостояния, решение о том, какие микросостояния использовать, не определяется нашими приборами или масштабом проблемы, его должен принимать тот, кто производит расчёт. Часто для физических систем люди используют набор микросостояний, которые отражают всю необходимую информацию, связанную с макросостоянием. Например, если макросостояние связано с шариками, находящимися на левой или правой стороне коробки, то нас, вероятно, не волнует ни скорость, ни масса, ни что-либо ещё, кроме положения шарика.

Другая проблема заключается в том, что кажется неправильным, что одна и та же физическая система с одним и тем же макросостоянием может иметь разные энтропии в зависимости от используемого нами представления микросостояния. Обычно мы ожидаем, что физические системы будут давать инвариантные результаты измерений независимо от того, какое внутреннее представление мы решили использовать для измерения. Но для энтропии это неверно. Мы должны вспомнить, что энтропия — это неопределённость системы и что определение энтропии полностью зависит от того, в чём мы не уверены, а для физических систем это микросостояния. Это похоже на то, как если бы кто-то спросил: «Из скольких частей состоит эта машина?», на что мы должны ответить: «Как вы определяете „часть“?». Когда мы спрашиваем: «Какова энтропия этого макросостояния?», нам нужно ответить: «Какие микросостояния мы используем?».

При всём этом в том, что говорит нам наша интуиция, есть доля правды, хотя она и не применима к общему случаю. Хотя энтропия системы меняется, когда мы меняем микросостояния, различия в энтропии макросостояний будут одинаковыми, если новые микросостояния равномерно умножают старые микросостояния. То есть, если каждое исходное микросостояние разбивается на одинаковое количество более тонких микросостояний, то энтропия каждого макросостояния увеличивается на константу. Однако мы уже запутались в терминологии, давайте рассмотрим пример.

Давайте снова возьмём 10 шаров в коробке и вычислим энтропию системы для нескольких различных макросостояний и микросостояний. Мы обозначим количество шаров на каждой стороне коробки через (L, R), где L — количество шаров слева, а R — количество шаров справа. Затем мы вычисляем энтропию для микросостояния сетки ячеек 2x1 (только левая и правая половины коробки) и для сетки ячеек 50x50.

И если мы посмотрим, то увидим, что энтропия в значениях микросостояний сетки 50x50 — это просто значения сетки 2x1 плюс константа. Разность энтропий в обоих случаях будет одинаковой. Это станет ещё понятнее, если мы математически покажем, как вычисляется энтропия. Для сетки 2x1 мы используем уравнение , а для сетки 50x50 мы используем . Математически мы видим, что это то же самое, что и энтропия сетки 2x1, смещённая на .

Можно представить, что если мы добавим ещё одно измерение для описания микросостояний, то энтропия снова увеличится на константу. Например, если бы каждый из 10 шариков мог быть одного из 3 цветов, то число микросостояний выросло бы в 3¹⁰ раз, и, следовательно, энтропия всей системы увеличилась бы в раз.

Наша интуиция была верна, когда мы использовали различные микросостояния, кратные друг другу, но эта интуиция даёт сбой, если микросостояния не так аккуратно кратны друг другу. Простой пример — если представить левую сторону коробки как одну ячейку, а правую — как сетку ячеек 50x25, то энтропия будет выглядеть совсем по-другому. Ниже снова приведена таблица, но с добавленной строкой наших негомогенных микросостояний. Пример того, как мы вычисляем энтропию макросостояния (3, 7): существует 120 равновероятных способов разместить 3 шара слева и 7 шаров справа, но шары справа также могут находиться в 1250⁷ разных состояниях, поэтому энтропия равна .

Забавно отметить, что когда все шары находятся слева, энтропия равна нулю, но когда все шары находятся справа, энтропия максимальна. И опять же, надеюсь, это имеет смысл на фоне нашего понимания энтропии — она измеряет неопределённость относительно наших микросостояний. Если мы знаем, что все шарики находятся слева, то мы знаем, что они должны быть в единственной левой ячейке, поэтому неопределённости нет. Если мы знаем, что все шарики находятся справа, то они могут быть в любом из 1250¹⁰ микросостояний, поэтому неопределённость велика.

Очевидно, что при измерении энтропии системы нам нужно быть внимательными и учитывать, какие микросостояния мы выбираем. К счастью, для большинства физических систем мы используем стандартные микросостояния в виде равномерной сетки координат и импульсов шаров (частиц) в системе. Другим стандартным микросостоянием, которое можно использовать, является непрерывное пространство положений и импульсов.

Непрерывные микросостояния

До сих пор мы рассматривали дискретные наборы микросостояний — например, шарики в ячейках. Но в физических системах микросостояния часто бывают непрерывными: положения и моменты могут изменяться в непрерывном пространстве. Как вычислить энтропию в таких условиях? Этот раздел не имеет отношения к остальной части статьи, но это интересный экскурс для изучения.

Давайте вернёмся к нашим 10 шарикам в двумерной коробке. Если каждый шарик может занимать любое место в квадрате, то микросостояние системы — это точка в 20-мерном пространстве (по 2 измерения на шар). Число возможных микросостояний бесконечно — и каждое из них имеет бесконечно малую вероятность.

В этой постановке мы используем функцию плотности вероятности , а энтропия становится непрерывным интегралом:

Это называется дифференциальной энтропией. Она обобщает энтропию Шеннона на непрерывные системы, хотя и имеет некоторые тонкости — она может быть отрицательной и не инвариантна при преобразованиях координат.

Если плотность однородна, скажем в области объёмом V, то энтропия становится равной:

Таким образом, энтропия по-прежнему растёт как логарифм объёма доступного состояния, как и в дискретном случае.

Этот формализм особенно естественен в квантовой механике, где волновая функция определяет плотность вероятности . Рассмотрим одномерную гауссову волновую функцию:

Его энтропия (в битах) равна:

Это показывает, что более широкие распределения имеют более высокую энтропию, как и ожидалось: более разбросанная волновая функция указывает на большую неопределённость в местоположении частицы.

Например:

• если , то

• если , то

Что опять же должно иметь смысл: когда мы менее уверены в системе, например, в том, где окажется частица при измерении, тогда у неё больше энтропия.

И ещё один момент: если пространство состояний не ограничено, как, например, импульс в классической механике, то энтропия может расходиться. На практике это не является проблемой, поскольку физические системы обычно имеют распределения вероятностей (например, гауссианы), которые достаточно быстро распадаются на бесконечности, чтобы энтропия оставалась конечной. Когда это не так, мы либо ограничиваем систему конечной областью, либо фокусируемся на разности энтропий, которая остаётся вполне определённой, даже когда абсолютная энтропия расходится.

Но давайте вернёмся к нашей основной теме и сделаем исторический обзор.

Стандартное использование энтропии

За 80 лет до того, как Клод Шеннон разработал теорию информации, Людвиг Больцман сформулировал статистическое определение энтропии для идеального газа. Он предположил, что энтропия S системы пропорциональна логарифму числа микросостояний W, соответствующих данному макросостоянию:

энтропия Больцмана

Это уравнение должно выглядеть знакомо: это равновероятностный частный случай энтропии Шеннона, которую мы использовали, только с изменением основания (с log₂ на ln) и масштабного коэффициента k_B (постоянная Больцмана). Связь между статистической механикой Больцмана и теорией информации Шеннона — это не просто историческое совпадение: и то, и другое количественно определяет неопределённость, будь то в физических состояниях или сообщениях.

Несколько лет спустя Джозайя Уиллард Гиббс обобщил определение Больцмана на случаи, когда микросостояния не являются равновероятными. Его формулировка остаётся стандартным определением энтропии в современной физике:

энтропия Гиббса

Формально она идентична энтропии Шеннона, отличаясь лишь основанием логарифма и физическими единицами. Но обобщение Гиббса стало значительным скачком: оно позволило термодинамике описывать системы в контакте с тепловыми ваннами, резервуарами частиц и другими средами, где распределения вероятностей по микросостояниям неоднородны. Благодаря этому применение энтропии вышло далеко за пределы идеальных газов — она охватывает химические реакции, фазовые переходы и статистические ансамбли всех видов.

Теперь, когда у нас есть формальное понимание энтропии и некоторая историческая справка, давайте попробуем понять, как энтропия связана с нашей Вселенной и, в частности, со временем.

Время

Какую роль во всём этом играет время?

Когда вы капаете молоко в чай, оно всегда растекается и смешивается, но вы никогда не наблюдаете обратного процесса, когда молекулы молока спонтанно отделяются от чая и возвращаются в аккуратную капельку. Когда океанские волны разбиваются о берег, брызги и пена рассеиваются, но мы никогда не видим, чтобы этот хаос вновь собрался в целостную волну, которая устремится обратно в море. Эти примеры взяты из лекции Ричарда Фейнмана об энтропии. Если бы вам показали запущенное задом наперёд видео этих событий, вы бы сразу поняли, что что-то не так. Поначалу это кажется очевидным, но на самом деле это не так, если мы просто посмотрим на законы физики. Все известные законы физики обратимы во времени (можно поспорить только насчёт коллапса волновой функции), что означает, что они выглядят одинаково при воспроизведении вперёд и назад. Отдельные молекулы подчиняются этим обратимым во времени законам, и всё же чашка чая становится мутной от постоянно примешивающегося молока.

Это подчёркивает фундаментальный парадокс: микроскопические законы физики обратимы во времени, а макроскопический мир — нет. Если взять видео двух атомов, отскакивающих друг от друга, и проиграть его в обратном порядке, оно всё равно будет выглядеть физически достоверным, но если проиграть видео смешивания молока с кофе в обратном порядке, оно будет выглядеть явно неправильно.

Мы хотим построить упрощённую модель времени таким образом, чтобы она отражала как обратимость микроскопических законов во времени, так и асимметрию макроскопического поведения. Представим себе полное состояние физической системы, например, ящика с частицами, как одну точку в высокоразмерном пространстве, называемом фазовым пространством, каждое измерение которого соответствует положению и импульсу частицы. С течением времени система прокладывает непрерывную траекторию через это пространство.

Управляют этой траекторией законы физики — такие как уравнения Ньютона, гамильтонова механика или уравнение Шрёдингера. Они детерминированы и обратимы во времени. Это означает, что если в любой момент времени обратить импульсы всех частиц, то система проделает обратный путь через пространство состояний.

Пока что всё является обратимым во времени, в том числе и этот взгляд на то, как Вселенная движется во времени. Но мы увидим, что даже в этой игрушечной модели у времени есть предпочтительное направление, стрела времени.

Ключ к этому лежит в грубой зернистости. Когда мы наблюдаем за миром, мы не видим всех микроскопических деталей. Вместо этого мы измеряем макросостояния: совокупные свойства, такие как температура, давление, положение объекта или распределение цветов в чашке чая. Каждому макросостоянию соответствует множество микросостояний, лежащих в его основе, и не все макросостояния одинаковы.

Например, рассмотрим коробку, скользящую по полу и приходящую в состояние покоя из-за трения. На микроскопическом уровне система представляет собой частицы, обменивающиеся импульсами, и всё это обратимо во времени. Но мы, конечно, не назовём это действие обратимым во времени, мы никогда не увидим, чтобы коробка спонтанно начала ускоряться после остановки. Но если мы возьмём момент после того, как коробка придёт в состояние покоя из-за трения, и обратим скорости всех частиц (включая частицы в полу, которые поглотили кинетическую энергию коробки в виде тепла), то коробка спонтанно начнёт двигаться и скатится в исходное положение. Это подчинялось бы законам Ньютона, но это астрономически маловероятно. Почему?

Количество микросостояний, в которых энергия распределяется в виде тепла (коробка находится в состоянии покоя, а молекулы в полу покачиваются), значительно превышает количество микросостояний, в которых вся эта энергия координируется для перемещения коробки. Макросостояние покоя имеет высокую энтропию, а макросостояние спонтанного движения — низкую. Когда система случайным или детерминированным образом эволюционирует от состояния низкой энтропии, она чрезвычайно более вероятно будет двигаться в сторону более высокой энтропии просто потому, что таких микросостояний больше.

Если бы вы обладали совершённым знанием обо всех частицах во Вселенной (то есть жили на уровне микросостояний), время, казалось бы, не имело бы направления. Но с точки зрения грубозернистого наблюдателя, каким являемся мы, энтропия имеет тенденцию к увеличению. Вот почему фильм о смешивании чая выглядит естественно, а обратный процесс — фальшиво. На уровне физических законов оба варианта справедливы. Но один из них типичен, а другой — астрономически редок, и всё потому, что мы грубозернисты.

Чтобы донести эту мысль до читателя, давайте снова рассмотрим шарики в коробке. Мы определим макросостояния, разделив коробку на сетку ячеек и подсчитав, сколько шариков находится в каждой ячейке.

Теперь предположим, что шарики движутся с помощью случайных небольших толчков (наша игрушечная модель микроскопической динамики). Со временем система, естественно, будет стремиться к наиболее вероятным макросостояниям, поскольку в наиболее вероятных макросостояниях гораздо больше микросостояний, в которые вы можете прийти. То есть энтропия со временем возрастает, но не из-за фундаментальной необратимости законов, а потому, что высокоэнтропийные макросостояния гораздо более типичны.

Если мы начали моделирование с того, что все шарики были упакованы слева, то это очень специфическое (низкоэнтропийное) макросостояние. По мере того как они разлетаются, количество совместимых микросостояний растёт, а вместе с ним и энтропия.

Это приводит к важному осознанию: энтропия увеличивается, потому что мы начали двигаться от состояния с низкой энтропией. Это часто называют гипотезой прошлого — постулатом о том, что Вселенная началась в чрезвычайно низкоэнтропийном состоянии. Из этого естественным образом вытекает второй закон термодинамики. Стрела времени возникает не из специфики самой динамики, а из статистической маловероятности её изменения на противоположную ввиду грубой зернистости, а также из того факта, что мы изначально находились в состоянии с низкой энтропией.

Можно представить, что когда система достигает почти максимальной энтропии, она уже не будет выглядеть обратимой во времени. Энтропия такой системы будет немного колебаться, поскольку энтропия по своей сути является статистической мерой, но эти колебания будут достаточно малы, чтобы их не заметить. Например, если на видео, где молоко наливают в чай (макросостояние с низкой энтропией), видно, что оно идёт вперёд, а не назад, то на видео, где уже смешанные молоко и чай (макросостояние с высокой энтропией) закручиваются в вихре, вы не сможете определить, идёт ли оно вперёд или назад.

Хотя существуют крошечные флуктуации энтропии, их недостаточно, чтобы объяснить крупномасштабные явления, которые иногда кажутся нарушающими только что установленный нами принцип, согласно которому энтропия всегда увеличивается со временем.

Нарушения Второго закона?

Некоторые примеры из реального мира противоречат утверждению, что энтропия всегда возрастает. Например, масло и вода разделяются после смешивания, пыль слипается в звёзды и планеты, а мы строим машины, такие как фильтры и холодильники, которые разделяют смешанные вещества. Разве это не нарушения закона?

Проблема в том, что мы рассматривали только положение молекул, в то время как физические системы обладают множеством различных свойств, которые допускают больше микросостояний. Например, если мы начнём рассматривать положение и скорость шариков в коробке, то энтропия может быть высокой, даже если все шарики находятся в левой части коробки, поскольку скорости шариков может отличаться друг от друга. Если бы все шары находились слева, а их скорости были бы одинаковыми, то энтропия была бы низкой. Если учесть ещё и скорость, то энтропия может увеличиться как от более разнесённых положений, так и от более разнесённых скоростей.

Когда вода и масло разделяются, положение молекул разделяется на верхнее и нижнее, что, казалось бы, уменьшает позиционную энтропию. Однако на самом деле такое разделение увеличивает общую энтропию системы. Почему? Молекулы воды предпочитают образовывать водородные связи с другими молекулами воды, а не взаимодействовать с молекулами масла. Когда молекулы воды вынуждены находиться рядом с молекулами масла в смешанном состоянии, они вынуждены принимать более ограниченное расположение, чтобы минимизировать неблагоприятные взаимодействия, что уменьшает количество доступных микросостояний. Когда вода и масло разделяются, молекулы воды могут свободно взаимодействовать с другими молекулами воды в большем количестве конфигураций, а молекулы масла могут более свободно взаимодействовать с другими молекулами масла. Это увеличение количества доступных микросостояний для молекулярного расположения и взаимодействий более чем компенсирует снижение энтропии позиционного смешивания. Таким образом, хотя энтропия уменьшается, если мы рассматриваем только общие положения молекул (смешанные или разделённые), общая энтропия увеличивается, когда мы учитываем все молекулярные взаимодействия, ориентации и локальные расположения. Это показывает, почему при расчёте энтропии необходимо учитывать все свойства системы.

Когда звёзды или планеты формируются из частиц пыли, плавающих в космосе, и слипаются под действием гравитации, кажется, что даже с учётом положения и скорости частиц энтропия может уменьшаться. Даже если частицы ускоряются, чтобы слипнуться вместе, они замедляются после столкновения, что, по-видимому, уменьшает энтропию. Это происходит потому, что мы снова не учитываем всю систему. Когда частицы сталкиваются друг с другом, их скорость немного уменьшается, превращая кинетическую энергию в излучение, в результате чего фотоны отправляются в космос. Если бы мы рассматривали систему, в которой излучение не допускается, то кинетическая энергия просто передавалась бы от одной частицы к другой за счёт изменения скорости, и энтропия системы всё равно бы увеличивалась из-за более высоких скоростей. Как только мы начнём учитывать энтропию положения, скорости и всех частиц в системе, мы сможем рассмотреть все микросостояния, которые одинаково вероятны, и вычислить правильную энтропию.

Аналогично, если мы рассмотрим всю систему вокруг холодильника, то уменьшение энтропии исчезнет. Энтропия от энергии, вырабатываемой для работы холодильника, и тепла, перемещаемого изнутри холодильника наружу, компенсирует уменьшение энтропии, вызванное охлаждением внутренней части холодильника. Можно добиться локального уменьшения энтропии, если энтропия всей системы продолжает расти.

Убедитесь, что при анализе энтропии системы учитывается вся система, положение, скорость и другие взаимодействия частиц, что все частицы включены и что вся система всесторонне анализируется.

Беспорядок

Энтропию иногда описывают как «беспорядок», но эта аналогия неточна и часто вводит в заблуждение. В статистической механике энтропия имеет строгое определение: она определяет количество микросостояний, совместимых с данным макросостоянием. Иными словами, энтропия измеряет нашу неопределённость относительно точной микроскопической конфигурации системы при наличии некоторого грубого макроскопического описания.

Откуда же взялась идея «беспорядка»?

Эмпирически макросостояния, которые мы обозначаем как «неупорядоченные», часто соответствуют гораздо большему числу микросостояний, чем те, которые мы считаем «упорядоченными». Например, в детской комнате гораздо больше конфигураций, где игрушки разбросаны беспорядочно, чем тех, где всё аккуратно расставлено по полкам. Поскольку разбросанные игрушки соответствуют большему числу микросостояний, их энтропия выше.

Но эта связь между энтропией и беспорядком не является фундаментальной. Проблема в том, что «беспорядок» субъективен — он зависит от человеческого восприятия, контекста и обозначения. Например, в нашем предыдущем примере с 1000 шариков, прыгающих в коробке, идеально однородная сетка шариков имела бы высокую энтропию из-за огромного количества возможных микросостояний, реализующих её. И всё же человеческому наблюдателю такая сетка может показаться весьма «упорядоченной».

Ключевой момент: энтропия объективна и чётко определена при наличии макросостояния и набора микросостояний, а «беспорядок» — это эвристическая концепция, ориентированная на человека, которая иногда, но не всегда, повторяет энтропию. Опираясь на «беспорядок» для объяснения энтропии, можно запутаться, особенно в системах, где визуальная симметрия или регулярность маскирует лежащую в основе статистическую структуру.

Заключение

Итак, вот несколько мыслей по поводу некоторых распространённых утверждений об энтропии:

• Энтропия — это мера беспорядка.

• «Беспорядок» — это субъективный термин для обозначения состояний системы, которые люди не находят полезными/приятными, и обычно энтропия гораздо выше, чем у „упорядоченных“ макросостояний, которые создают люди. Поэтому, когда энтропия увеличивается, более вероятно, что мы окажемся в неупорядоченном состоянии, хотя это и не гарантировано.

• Энтропия всегда возрастает в закрытой системе.

• Это статистическое утверждение, которое для всех практических целей верно, но не гарантировано и может не сработать, если вы рассматриваете очень маленькие изолированные системы или измеряете их вплоть до мельчайших деталей. Оно также предполагает, что вы начали в состоянии с низкой энтропией, что даёт вашей системе пространство для роста энтропии. Из этого следует, что, поскольку в нашей Вселенной наблюдается рост энтропии, она должна была начаться в низкоэнтропийном состоянии.

• Тепло перетекает от горячего к холодному из-за энтропии.

• Тепло течёт от горячего к холодному, потому что число способов, которыми система может быть неоднородной по температуре, намного меньше числа способов, которыми она может быть однородной по температуре, и поэтому, когда система «случайно» переходит в новые состояния, она статистически оказывается в состояниях, которые являются более однородными.

• Энтропия — единственный необратимый во времени закон физики.

• Все фундаментальные законы физики обратимы во времени, но при грубой зернистости и старте из состояния с более низкой энтропией система статистически перейдёт в состояние с более высокой энтропией. Это означает, что если система уже находится в состоянии, близком к максимуму энтропии (либо из-за её конфигурации, либо из-за выбора грубой зернистости), или мы не проводим грубую градацию, то энтропия не будет выглядеть обратимой во времени.