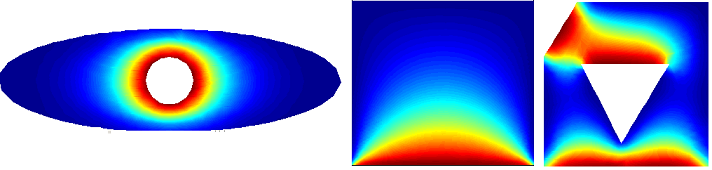
Метод Finite Volume (FVM)
В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.
Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.
Некоторые плюсы FVM:
- сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
- высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
- легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.
Метод FVM реализуем на примере уравнения теплопроводности:
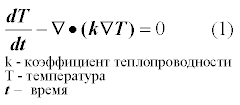
Итак основные шаги при реализации FVM:
- Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
- Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
- Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.
Дискретизация по времени.
Для производной по времени используем стандартный простейший метод Эйлера.Это будет явная схема по времени, где берутся искомые с предыдущего шага.А на первом шаге задаются как начальные условия.

Немного теории или первый шаг в реализации FVM
Используя теорему о дивергенции интеграл по объему преобразуется в интеграл по площади.Смысл в том что интегрирование по всему внутреннему объему нашего элемента мы заменяем на интегрирование только по поверхности этого объема.Эта формулировка больше подходит для 3D случая.Для 2D у нас будет вместо объема V — площадь элемента, а вместо S — периметр элемента.Тоесть получается что интеграл по площади заменяется интегралом по периметру.Фактически у нас понижается степень производной.Если например была вторая производная то остается только первая, если была первая — то вместо производной будет искомая переменная.Надо только не забывать что имеем дело не с обычной производной а с дивергенцией.
Итак второй терм в нашем уравнении после интегрирования преобразуется так:
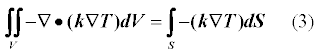
FVM на стандартной прямоугольной сетке

На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.
Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.
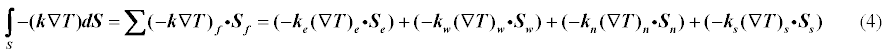
Индексы e w n s здесь обозначают что выражение или переменная вычисляется в центре соответствующей грани.
Теперь соберем вместе полученные упрощения частей исходного дифф уравнения — термы (2) и (4).Получим первую ступень аппроксимации:

Теперь нам осталось только до конца аппроксимировать (4), поскольку туда входит градиент, его то нам и надо перевести в численную форму.Фактически эта сумма представляет сумму потоков тепла через грани.Наш случай упрощается для прямоугольной сетки, т.к у нормали к грани остается только 1 компонент — либо вдоль оси х либо вдоль y.
Разберем подробно этот процесс на примере грани e.

Теперь подставим вместо суммы в уравнении (5) полученные дискретные аналоги для 4-х граней:
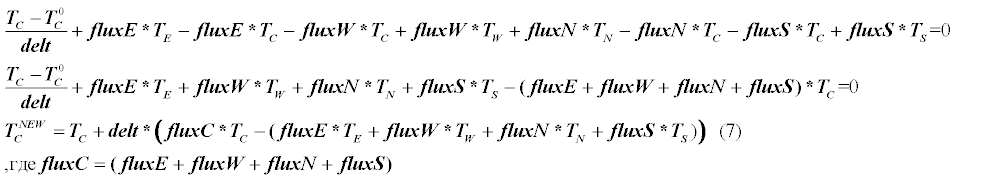
Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.
Граничные условия на прямоугольной сетке
На рисунке показан элемент С у которого грань e находится на границе и значения температуры на этой грани известны — либо как заданная температура либо как заданный поток тепла через грань.

Мы рассмотрим только 2 вида граничных условий.
- Задана температура Tb на границе
- Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)
Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.
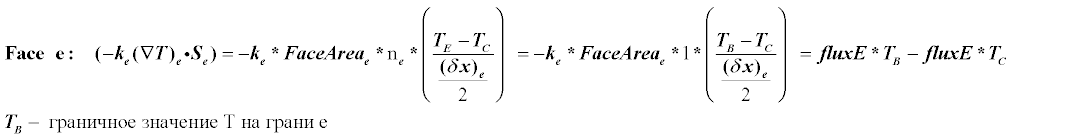
Пример численных расчетов на прямоугольной сетке
В качестве примера рассмотрим область разбитую на 9 элементов, сетка 3*3.На первых слайдах применены следующие граничные условия: по 3 сторонам температура T=0, снизу задана температура T=240.На второй строке слайдов по бокам заданы граничные условия с потоком Flux=0, сверху T=0, снизу T=240.По каждому случаю 2 картинки, одна с разбивкой области 3*3 элемента, вторая 40*40.
public void RunPhysic()
{
double Tc, Te, Tw, Tn, Ts;
double FluxC, FluxE, FluxW, FluxN, FluxS;
double dx = 0;
double Tb = 240;
double Tb0 = 0;
int i, j;
for (i = 0; i < imax; i++)
for (j = 0; j < jmax; j++)
{
Tc = T[i, j];
dx = dh;
if (i == imax - 1) { Te = Tb0; dx = dx / 2; }
else
Te = T[i + 1, j];
FluxE = (-k * FaceArea) / dx;
if (i == 0) { Tw = Tb0; dx = dx / 2; }
else
Tw = T[i - 1, j];
FluxW = (-k * FaceArea) / dx;
if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; }
else
Tn = T[i, j + 1];
FluxN = (-k * FaceArea) / dx;
if (j == 0) { Ts = Tb; dx = dx / 2; }
else
Ts = T[i, j - 1];
FluxS = (-k * FaceArea) / dx;
FluxC = FluxE + FluxW + FluxN + FluxS;
T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts));
}
}
//Insulated
public void RunPhysic2()
{
double Tc, Te, Tw, Tn, Ts;
double FluxC, FluxE, FluxW, FluxN, FluxS;
double dx = 0;
double Tb = 240;
double Tb0 = 0;
int i, j;
for (i = 0; i < imax; i++)
for (j = 0; j < jmax; j++)
{
Tc = T[i, j];
dx = dh;
Te = 0; Tw = 0;
if (i == imax - 1)
FluxE = 0;
else
{
Te = T[i + 1, j];
FluxE = (-k * FaceArea) / dx;
}
if (i == 0)
FluxW = 0;
else
{
Tw = T[i - 1, j];
FluxW = (-k * FaceArea) / dx;
}
if (j == jmax - 1) { Tn = Tb0; dx = dx / 2; }
else
Tn = T[i, j + 1];
FluxN = (-k * FaceArea) / dx;
if (j == 0) { Ts = Tb; dx = dx / 2; }
else
Ts = T[i, j - 1];
FluxS = (-k * FaceArea) / dx;
FluxC = FluxE + FluxW + FluxN + FluxS;
T[i, j] = Tc + delt * (FluxC * Tc - (FluxE * Te + FluxW * Tw + FluxN * Tn + FluxS * Ts));
}
}

FVM в задачах со сложной геометрией
Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.
Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».
На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

Схема расчетов выглядит примерно так.

Второй терм здесь это кросс-диффузия, она будет тем больше, чем больше расхождение между векторами Ef и Sf, если они совпадают, то она равна 0.
Распишем сначала ортогональную часть(способ minimum correction).

В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.
Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:
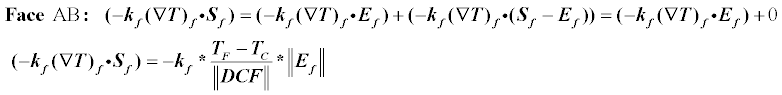
public void Calc()
{
double bc, ac;
double sumflux;
double[] aa = new double[6];
double[] bb = new double[6];
int e;
for (e = 0; e < elementcount; e++)
{
Element elem = elements[e];
int nf;
bc = 0;
ac = 0;
sumflux = 0;
for (int nn = 0; nn <6; nn++)
{
aa[nn] = 0;
bb[nn] = 0;
}
for (nf = 0; nf < elem.vertex.Length; nf++)
{
Face face = elem.faces[nf];
Element nb = elem.nbs[nf];
if (face.isboundary)
{
if (face.boundaryType == BoundaryType.BND_CONST)
{
double flux1;
double flux;
flux1 = elem.k * (face.area / elem.nodedistances[nf]);
Vector2 Sf = face.sf.Clone();
Vector2 dCf = elem.cfdistance[nf].Clone();
if (Sf * dCf < 0)
Sf = -Sf;
//1) minimum correction
//Vector2 DCF = elem.cndistance[nf].Clone();
Vector2 e1 = dCf.GetNormalize();
Vector2 EF = (e1 * Sf) * e1;
flux = elem.k * (EF.Length() / dCf.Length());
ac += flux;
bc += flux * face.bndu;
bb[nf] = flux;
}
else if (face.boundaryType == BoundaryType.BND_INSULATED)
{
double flux;
flux = 0;
ac += flux;
bc += flux * face.bndu;
bb[nf] = flux;
}
}
else
{
double flux1;
double flux;
flux1 = -elem.k * (face.area / elem.nodedistances[nf]);
Vector2 Sf = face.sf.Clone();
Vector2 dCf = elem.cfdistance[nf].Clone();
if (Sf * dCf < 0)
Sf = -Sf;
Vector2 DCF = elem.cndistance[nf].Clone();
Vector2 e1 = DCF.GetNormalize();
//corrected flux
//1) minimum correction
Vector2 EF = (e1 * Sf) * e1;
flux = -elem.k * (EF.Length() / DCF.Length());
sumflux += flux * nb.u;
ac += -flux;
aa[nf] = -flux;
}
}
elem.u = elem.u + delt * (bc - sumflux - ac * elem.u);
}
}
Примеры и проверка результатов
Проверка проводилась сравнением результатов в Матлаб и моей реализации. Mesh использовалась одинаковая, выгружалась из Матлаб и загружалась в прогу.На некоторые артефакты-треугольники не обращайте внимания, это просто непонятный глюк отрисовки.

Описание структуры исходников
Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.
Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:
//p.out
public void SetPeriodicBoundary()
Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)
##Points — координаты точек, первая строка — х, вторая -y.
##Triangle — треугольники, первая строка — индекс 1-ой вершины в массиве ##Points,2 и 3 строки — индексы 2 и 3 вершины треуольника.
##Boundary — грани, первая строка — индекс 1-ой вершины грани ,2-я — индекс второй вершины, пятая строка — группа, шестая — домен
Гитхаб с исходниками
- heat2PolyV2 — финальная версия
- other\heat2Utrianglestatic — реализован пример из книги p346 versteeg_h malalasekra_w_ An_introduction_to_computational_fluid…
- other\water2dV2 — попытка решения уравнений Навье-Стокса частично используя FiniteVolume
- matlab — m файлы примеров pde toolbox + savemymesh.m который выгружает готовый .out файл для heat2PolyV2
- Versteeg HK Malalasek Introduction to computational fluid dynamics The finite volume method — уже есть второе издание
- F.Moukalled L.Mangani M.Darwish The finite volume method in computational fluid dynamics 2016г — вышла недавно (чуть ли не вчера:)
- Патанкар С.-Численные методы решения задач теплообмена и динамики жидкости-Энергоатомиздат (1984)
- Патанкар С.В.-Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах-МЭИ (2003)
- Computational methods for fluid dynamics Ferziger JH Peric 2001 — хоть напрямую и не относится к FVM, но оч много полезного
Комментарии (14)

Uranix
30.01.2016 09:25+1А с чем в Матлабе сравнивали? Я помню там есть PDEToolbox, но он конечно-элементный, а не конечно-разностный. У вас же на картинках из Матлаба явно результаты расчета какого-то конечно-объемного метода.
А для проверки критичности кросс-диффузии попробуйте сетку сильно растянуть по одной координате и запустить просто с точечным начальным условием. В моем понимании, вместо кругового пятна у вас получится эллиптическое.
scifix
30.01.2016 13:05Да, как ни странно, но это конечноэлементный pde toolbox, другие встроенные в нем и не идут вроде как.Насчет растяжки действительно мысль!)

sci_nov
30.01.2016 10:23+1Объясните, почему вы интегрируете одну часть уравнения (1), а вторую — не интегрируете, и приравниваете обе части в (5)?

scifix
30.01.2016 15:53вот глазастые академики то пошли) да тут ошибка, просто сначала писались исходники а потом формулы, а в исходниках этот момент упустил из виду. Исправление вобщем то простое — нужно для каждого элемента заменить константу (delt) на (delt/ElementArea) в 2D или (delt/ElementVolume) 3D. Так же в частном случае можно просто учесть ее как множитель в задании общего значения delt.

DrZer0
30.01.2016 10:50Можете рассказать, исходя из какого соображения выбираете dt?

scifix
30.01.2016 13:16-1При использовании разных численных методов уже скопился некоторый интуитивный опыт выбора dt. В случае FVM на стандартной сетке — выбор dt должен совпадать с конечно-разностным способом — условием куранта.Это ведь явный метод — тут особо не повыбираешь время, на каком работает то и берешь) А вобще это тема конечно для отдельной статьи — цель была скорее в применении FVM для сложной геометрии

DrZer0
01.02.2016 09:29Спасибо за ответ, и отдельное спасибо за статью. Довольно редко встречаются работы, позволяющие перейти от формулы к счёту.

FransuaMaryDelone
30.01.2016 12:30чего это в (1) минус у второго слагаемого? У Вас температура в объеме растет, когда тепло из него вытекает — получается же.

scifix
30.01.2016 15:20Отличный вопрос) минус получается потому что поток тепла идет против градиента температуры(поток положителен в сторону убывания теипературы ). Вобщем это следует из закона фурье, где тоже минус.

mickvav
31.01.2016 22:15+1А идея сравнивать с аналитическими решениями чужда? А порядок аппроксимации какой?

scifix
01.02.2016 06:26-1не вижу большого смысла сравнивать с аналитикой при визуальном сходстве с матлабом — все так и не новый метод численного решения разрабатываю.Порядок аппроксимации не должен сильно отличатся от стандартного FDM, специальные исследования не проводил


Shablonarium
А почему в центре белые области? Нулевая теплопроводность?
scifix
Как видно из Mesh разбиения области на треугольники, там просто дырка изначально задумана, как если бы вы изучали температуру бублика)
Естественно нет смысла рассматривать температуру воздуха в этой дырке, поскольку она известна