Если посмотреть на последовательность кадров, в которых движется камера, то мозг легко воспринимает геометрическую структуру содержимого. Однако, в компьютерном зрении это не тривиальная проблема. В этой статье я постараюсь описать возможное решение этой задачи.

Перед прочтением этой статьи не помешает внимательно прочитать статью «Основы стереозрения».

Итак, перед нами стоит задача превращения последовательности двумерных изображений в трехмерную структуру. Задача это не простая, и нужно ее упрощать.
Во-первых, предположим, что кадра у нас только два. Обозначим их как A и B.
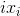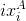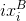Во-вторых, будем работать с конечным множеством точек, соответствующих друг другу на кадрах A и B. Точки на изображении обозначим как . Тогда точки на кадрах A и B будут и . Каждая пара точек соответствует точке в трехмерном пространстве .

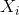Теперь необходимо определиться как искать 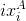и 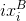. Для этого на первом кадре выберем точки, с наибольшей контрастностью — «особенные» точки (features). Для этого можно использовать surf, fast или что-нибудь другое. Эти точки и будут 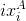. Затем необходимо найти соответствия этим точкам на втором кадре при помощи того же алгоритма surf или оптического потока. А это уже точки .

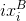А теперь мы подошли к центральному вопросу этой статьи: как из точек 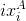и 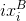(точек-соответствий, point correspondences) получить координаты точек и положение камеры в пространстве? Сначала необходимо разобраться с тем, как же точка она попадает на изображение. Нужно построить математическую модель камеры.

Модель проективной камеры

Так как вы, вероятно, уже прочитали статью «Основы стереозрения», эта формула должна быть знакома:
.
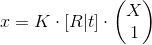Или если описать более полно:
.
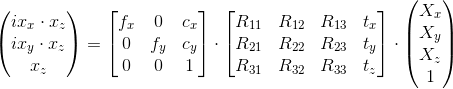Здесь X — это трехмерная точка в пространстве.
x — это координата точки на изображении в однородных координатах, и 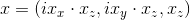, т. е. перевод в обычные координаты изображения будет таким: .
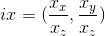Процесс перевода точки в пространстве в координаты изображения можно разбить на два этапа, реализуемыми двумя матрицами в формуле:

1. [R|t] — R и t представляют собой положение камеры в пространстве. На этом этапе координаты точек переводятся в локальные координаты камеры. R — матрица поворота размером 3x3, t — трехмерный вектор смещения — вместе они составляют матрицу перехода [R|t] (размером 3x4), она определяет положение камеры в кадре. [R|t] — эта то же, что и видовая матрица в трехмерной графике (если не брать в расчет, что она имеет размер не 4x4).
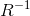   — это матрица поворота камеры, 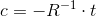— трехмерные координаты точки расположения камеры в пространстве. R и t называют внешними параметрами камеры.
2. K — матрица камеры. Локальные координаты точек переводятся в однородные координаты изображения. f_x, f_y — фокальное расстояние в пикселях, c_x, c_y — оптический центр камеры (обычно это координаты центра изображения). Эти параметры называют внутренними параметрами камеры.

Важным свойством этой модели является то, что точки лежащие на одной прямой в пространстве будут также лежать на одной прямой на изображении.
На самом деле, описываемая модель может быть очень неточной. В реальных камерах вступают в игру линзовые искажения, из-за которых прямые линии становятся кривыми. Это искажение называются дисторсией. Существуют разные модели, исправляющие эти искажения. Здесь есть некоторые их реализации. Параметры этой модели также входит в понятие внутренних параметров камеры.
С учетом дисторсии наша формула усложняется:
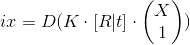, где D(X) — функция, принимающая однородные координаты точек изображения и возвращающая обычные координаты на изображении. Также позже нам понадобится обратная функция — InvD(ix).
Внутренние параметры камеры должны быть известны заранее. Выяснение этих параметров — это отдельная тема, будем считать, что они уже есть.

Искажения дисторсии не зависит от глубины видимых точек, а только координат на изображении. А значит «исправить» изображение (получив прямые линии там, где они и должны быть) можно не зная внешних параметров камеры и координат точек в пространстве. Дальше тогда можно использовать модель камеры без функции D.

Изображение с дисторсией слева, и справа — «исправленное» от линзовых искажений изображение. Видно, что линии стали прямыми.

Нормализация точек

Мы договорились, что внутренние параметры нам известны, известны и координаты точек на изображении, а значит, остается найти [R|t] и X_i (положения камеры и точек в пространстве).
Наша формула выходит уже немного сложной, надо ее упрощать. Для начала сделаем так:

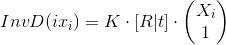
Выражение остается справедливым. Продолжим:

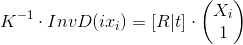
Обозначим 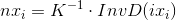(а если без дисторсии, то 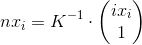). Так как все параметры известны, nx_i можно посчитать заранее. Вспомнив как выглядит матрица K, можно понять, что nx_z = 1. Это поможет при дальнейших расчетах. В результате формула становится проще: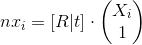


nx_i — это нормализованные точки изображения.

Фундаментальная и сущностная матрицы

Итак, предположим, у нас есть два изображения, полученные от одной камеры. Нам неизвестны положения камер и координаты точек в пространстве. Договоримся ввести расчеты относительно первого кадра. Так получается, что R^A = I (I — единичная матрица), t^A = (0, 0, 0). Положение камеры в кадре B обозначим просто как R и t (т. е. R^B = R, t^B = t). [R|t] — это матрица координат второго кадра, и оно же — матрица смещения положения камеры от кадра A к кадру B. В итоге имеем получаем такую систему (без учета дисторсии!):

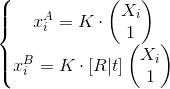
Используя фундаментальную матрицу F (fubdamental matrix), получим такое уравнение:

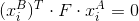
Также заметим, что F имеет размер 3х3 и должна иметь ранг равный 2.
Из фундаментальной матрицы F уже можно получить необходимые нам R и t. Однако дисторсия все портит, с ее учетом зависимость точек между кадрами будет нелинейная, и это уже не будет работать.
Но перейдем к нормализованным точкам и используем сущностную матрицу E (essential matrix). Все будет почти тем же, но проще:
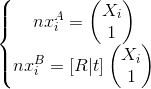— система уравнений для сущностной матрицы;
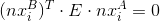— уравнение для нее же.
А тут мы можем спокойно брать в расчет дисторсию.
Фундаментальная и сущностная матрицы связаны таким образом:

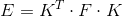
Теперь перед нами встала задача нахождения либо фундаментальной матрицы F, либо сущностной матрицы E, из которой позже сможем получить на R и t.

Вычисление сущностной матрицы (8-ми точечный алгоритм)

Вернемся к уравнению:

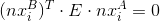
Эту же формулу можно переписать в таком виде (вспоминаем, что 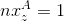и ):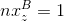
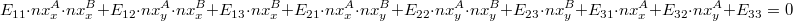, здесь опущен параметр i ради удобства, но имеем ввиду что это справедливо для каждой точки.
Введем вектор e и матрицу M:


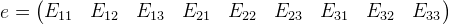
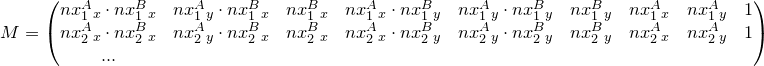
Тогда всю систему уравнений можно представить в виде:

Получаем однородную систему уравнений, решив которую, получим E из е. Очевидным решением здесь является нулевой вектор, но нас явно интересует не он. Для решения необходимо минимум 8 точек.

Решение систем однородных уравнений при помощи сингулярного разложения

Сингулярное разложение — это декомпозиция матрицы, приводящее ее к такому виду:
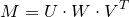, где U, V — ортогональные матрицы, W — диагональная матрица. При этом диагональные элементы матрицы W принято располагать в порядке убывания. Также ранг матрицы W — это и ранг матрицы M. А так как W — диагональная матрица, то ее ранг — это количество ненулевых диагональных элементов.

Итак, было дано уравнение вида:
, где M — известная нам матрица, e — вектор, который на необходимо найти.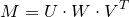

Строки V^T, которым соответствует нулевой диагональный элемент W на этой же строке, являются нуль-пространствами матрицы M, т. е. в данном случае являются линейно-независимыми решениями нашей системы. А так как элементы W располагаются в порядке убывания, то смотреть нужно последний элемент матрицы W. И решением будет последняя строка .
При расчете сущностной матрицы, используя 8 точек, последний элемент матрицы W должен быть равен нулю — W₉₉=0, но на практике, в следствии ошибок, там будет какое-то ненулевое значение, и по величине этого значения можно оценить величину этой ошибки. При этом мы получим лучшее решение.
Тем не менее, найденное нами решение — не единственное, более того, решений будет бесконечно много. Если умножить найденное решение на какой-либо коэффициент, оно все-равно останется решением. Таким образом в уравнении спрятался коэффициент s (который может быть любым):
.
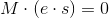Правда, все эти решения будут линейно зависимыми, а интересовать нас будет только одно из них.
Отсюда и матрица E может также масштабироваться. Вот только расчеты ведутся в однородном пространстве и, как следствие, от масштабирования (т. е. от коэффициента s) не зависят.
Наверное, стоит масштабировать получившуюся матрицу E так, чтобы E₃₃ = 1.

Вычисление сущностной матрицы (7-ми точечный алгоритм)

Можно обойтись и 7-ю точками.
Если мы возьмем только 7 точек, то M будет матрицей размером 7x9.
Вернемся к выражению:

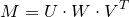
W — будет также матрицей размером 9x9, как и раньше, но теперь не только W₉₉ будет равно нулю (ну опять же без учета ошибок вычислений), но и W₈₈. Это значит, что имеем два линейно-независимых решения уравнения . Из них получим две матрицы E₁ и E₂. Решением будет выражение .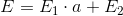
Сущностная матрица, как и фундаментальная, должна иметь ранг равный двум, а так как она имеем размер 3x3, то значит определитель матрицы равен 0 — 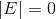. Следовательно 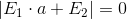. Если расписать это уравнение, то получим кубическое уравнение, имеющее 1 или 3 решения . А значит получим одну или три матрицы E.
Расписывать решение этого уравнения я не буду (оно объемное, ну и считайте это домашним заданием). В крайнем случае можете просто посмотреть сразу реализацию в opencv.

Уточнение сущностной (фундаментальной) матрицы

Так как все в этом мире несовершенно, то мы будем постоянно получать ошибки, с которыми нам необходимо бороться. Так сущностная матрица должна иметь ранг равный 2 и следовательно 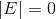. На практике, однако, это будет нет так.
Чтобы увидеть в чем это выражается, возьмем фундаментальную матрицу. Сущностная матрица / фундаментальная матрица — разница лишь в том, с какими точками мы работаем (нормализованными или точками на изображении).
Луч, выпущенный из точки кадра A, ляжет в кадр B как прямая линия (или не совсем из-за дисторсии, но забудем про нее). Допустим матрица F — это фундаментальная матрица кадров A и B ().
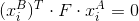Тогда если выпустить луч из точки , то в получим прямую l на кадре B — . Эта прямая называется эпиполярной линией, т. е. 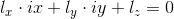, где ix, iy — координаты точки на изображении. И то же условие для точки на изображении с однородными координатами — 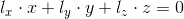. Точка 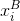будет лежать на этой прямой, поэтому 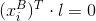. Отсюда и выходит общая формула — .

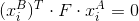На картинке изображен пример эпиполярных линий, полученных из правильной фундаментальной матрицы (ранг которой равен 2, картинка справа) и неправильной (слева).
Чтобы получить правильную фундаментальную матрицу, воспользуемся свойством сингулярного разложения — приближать матрицу к заданному рангу:
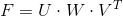. В идеале W₃₃ (последний элемент диагонали) должен быть равен нулю. Введем новую матрицу W’, которая равна W, только у которой элемент W'₃₃ = 0.
Тогда исправленный вариант: .
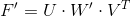Ровно тот же принцип работает и для сущностной матрицы.

Нормализованная версия алгоритма

Чтобы уменьшить ошибку, получаемую при расчетах, точки трансформируют к определенному ввиду. Выбираются такие матрицы T^A и T^B, которые (каждый независимо и на своем кадре) смещают среднюю координату точек в точку (0, 0) и масштабируют так, чтобы средняя дистанция дистанция до центра была равна :

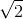А матрицы T^{A, B} имеют вид: 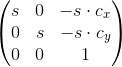, где c — средняя координата точек кадров, s — коэффициент масштаба.
После этого вычисляем сущностную матрицу как обычно. После необходимо ее уточнить, как было описано выше. Обозначим полученную матрицу как E^t.
Итоговая сущностная матрица — .
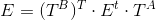В итоге:
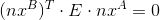
Опять же, если необходимо найти фундаментальную матрицу, все принципы сохраняются.

Получение положения камеры из сущностной матрицы

Введем матрицу H:
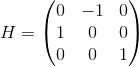
Используем сингулярное разложение на сущностной матрице:
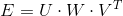
Тогда получаем такие решения:



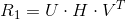
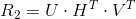
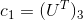
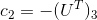, где 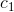, 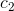— координаты положения камеры.
Нам же необходимо положение камеры в локальных координатах самой камеры: .
Выходит четыре решения: .
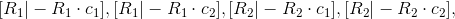В случае 8-ми точечного алгоритма, выбираем из 4-ёх решений. В случае 7-ми точечного алгоритма, выйдет три сущностные матрицы, из которых получится 12 решений. Выбрать нужно только одно, то, которое будет давать меньше ошибок.

Вырожденные случаи

Снова вернемся к вычислению сущностной матрицы. У нас было уравнение:

Далее мы его решали при помощи сингулярного разложения:

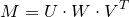
Решения данного уравнения зависит от ранга матрицы W, ну или от количества нулей в диагонали этой матрицы (мы же помним, что это отражает ранг матрицы). Вот только с учетом погрешности, считаем нулем в данном случае число, достаточно близкое к нулю.
Имеем такие варианты:

• Нулей нет. Нет решений, вероятно ошибка вышла слишком большой.
• Один нуль. Одно решение, случай при котором число точек больше, либо равно восьми.
• Два нуля. Одно или три решения. Использовалось семь или более точек.
• Три нуля. Тогда должно быть верно условие 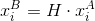. Такое возможно, если камера не смещалась от кадра к кадру, был только поворот, т. е. t = (0, 0, 0). Либо все точки лежат на одной плоскости. Во втором случае еще есть возможность найти координаты этих точек и положение камеры, но уже другими способами.

Вычисление координат точек в пространстве

Допустим сейчас у нас есть больше, чем два кадра — A, B, C, …
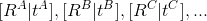— положение камер кадров A, B, C,…
— нормализованные точки
Необходимо найти точку

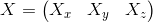
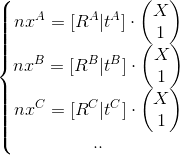
Представим эту систему так:


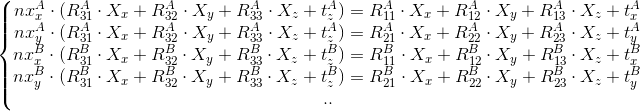
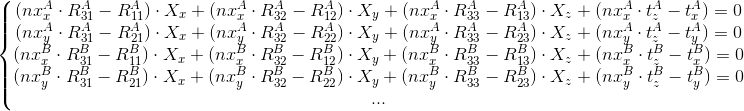
В матричном виде:


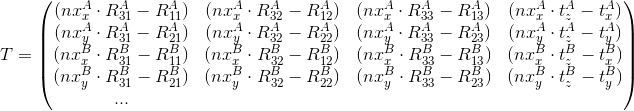
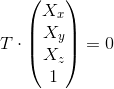
С помощью сингулярного разложения находим вектор , который 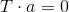(способом, описанном выше). Тогда 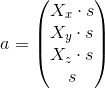, где s — какой-то неизвестный коэффициент. Выходит .

Оценочная функция

Оценочные функции (cost functions) необходимы, чтобы получив какие-то результаты, оценить насколько достоверными они являются, или сравнить их с другими.
Возьмем нашу модель:
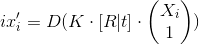— предполагаемый результат.
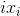— реальное значение точки.
Отсюда квадрат ошибки для i-ой точки будет: .
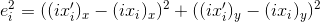На практике одни точки будут давать более достоверные результаты, чем другие. А некоторые вообще явно будут давать неправильные. В результате возникает необходимость выбрать из общего массива точек только те точки, которым можно доверять, а остальные просто выбросить из расчетов.
Самый простой способ выбрать “достоверные” точки — выбрать какой-то лимит (допустим, 5 пикселей), и брать только те точки, которые дают ошибку меньше этого лимита (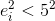). Тут же следует отметить, что необходимо учитывать, что точка должна лежать перед камерой в обоих кадрах, иначе ее явно необходимо отбросить.
Таким образом, можно ввести оценочную функцию — количество достоверных точек. И при сравнении, выбирать тот результат, который дает большее количество “достоверных” точек.
А можно воспользоваться другим, более “тонкой” функцией:
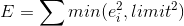, где limit — это выбранный нами лимит (в 5 пикселей).
Лучшим будет тот вариант, который будет давать меньшее значение. Понятно, что и здесь следует убирать “недостоверные” точки для будущих расчетов.

Метод RANSAC

1. При вычислении сущностной матрицы необходимо отбрасывать “недостоверные” точки, так как они приводят в существенным ошибкам в расчетах. Определить набор подходящих точек можно при помощи алгоритма RANSAC.
   Повторяем цикл заданное количество раз (например, 100, 400):
   
   • Выбираем случайным образом минимальный набор точек для расчетов (у нас это 7);
   • Вычисляем сущностные матрицы из этого набора (напоминаю, может получится либо одна матрица, либо три)
   • Оценочной функцией вычисляем достоверность каждой матрицы
2. Из предыдущего цикла выбираем сущностную матрицу, которая дает лучший результат;
3. Выбираем точки для расчетов, которые дают ошибку при полученной сущностной матрице ошибку меньше заданного порога;
4. Из полученного набора точек вычисляем итоговую сущностную матрицу.

Общий алгоритм

1. Находим «особенные» точки на первом кадре
2. Определяем точки-соответствия между двумя изображениями.
3. Находим сущностную (или все-же фундаментальную) матрицу, соответствующую этим двум изображениям при помощи RANSAC.
4. У нас будет одно или три решения, из которых получим 4 или 12 возможных матриц [R|t]. Имея положение камер в обоих кадрах, рассчитываем координаты точек в пространстве для каждой возможной матрицы. Из них выбираем лучшую, используя оценочную функцию.

Что дальше?

Изначально мы исходили из предположения, что кадра у нас было всего два.
Чтобы работать с последовательностью кадров, нужно просто разбить последовательность на последовательные пары кадров. Обрабатывая пары кадров, мы получаем смещение камеры от одного кадра к другому. Из этого можно получить координаты положения камеры в остальных кадрах.

Получив главное — положения камер, можно действовать по-разному:

• По точкам-соответствиям получить трехмерные координаты точек в пространстве, выйдет облако точек, которое можно превратить в трехмерную модель
• Использовать фундаментальную матрицу для расчета карты глубины.
• При помощи двух кадров инициализировать карту для SLAM, используя рассчитанные координаты точек в пространстве, можно проще и быстрее получить координаты положения в следующих кадрах.
• ну и другое

В общем, действовать можно по-разному, применяя разные методы, в том числе и те алгоритмы, которые были описаны — не единственные.

Литература

Fundamental matrix, Essential matrix, Eight-point algorithm — больше информации в википедии
Hartley, Zisserman — Multiple View Geometry in Computer Vision — спонсор этой статьи