Проблема факторизации напрямую связана с определением криптостойкости RSA, которое базируется на предположении, что не существует быстрых алгоритмов факторизации, которые за короткое время позволили бы взломать код, а если через некоторое время и получится это сделать, то данные потеряют свою актуальность. В этой статье мы протестируем и сделаем выводы по одному из способов факторизации.
Приведём определение факторизации.
Факторизацией целого числа называется его разложение в произведение простых сомножителей. Такое разложение, согласно основной теореме арифметики, всегда существует и является единственным (с точностью порядка следования множителей).
Будем обозначать число, которое требуется разложить буквой N, а два сомножителя, в результате умножения которых получим N, как a и b.
Алгоритм факторизации Ленстры (факторизация на эллиптических кривых) является одним из самых быстрых методов факторизации. Он имеет много общего с методом Полларда (p – 1), но работает значительно быстрей, следует отметить, что он является субэкспоненциальным методом. Главная особенность алгоритма – это то, что время, затраченное на факторизацию, зависит не от размерности N, а от размера наименьшего делителя числа N.
Подробно про этот метод вы сможете почитать из материала в списке использованной литературы, но всё же приведём основные стадии алгоритма.
В арифметике полей нет операции деления, которая необходима в формулах для нахождения координат точек, так что мы преобразуем выражение в виде умножения, а обратный элемент ищем по расширенному алгоритму Евклида. К тому же каждое новое вычисление мы производим по модулю числа N.
Алгоритм завершит свою работу, когда будет найден Н.О.Д.(N, P), который больше 1 и меньше N. Во избежание ошибки в ответе, функция нахождения Н.О.Д. должна проверять только положительные значения.
Рассмотрим график времени, которое нам понадобится для факторизации разных чисел. (Результат приведён из написанной мною программы)
Так как кривая генерируется из случайных значений, то время факторизации при каждом новом запуске программы будет разным. Смотря удачная ли кривая нам попадётся. По этому, попробуем взять эти же числа и выполнить факторизацию ещё несколько раз и сверим результаты.
И для закрепления сделаем последний замер.
Как мы видим на последнем графике, время затраченное на последнее число заметно уменьшилось, это характеризуется тем, что кривая генерируется случайным образом. Следует заметить, что время, затраченное на выполнение алгоритма, зависит и от значения B, которое мы вводим. Я старался брать значение приближённые к значениям двух сомножителей (a и b), но если вы будете выполнять операцию над числом, где изначальные множители не известны даже приблизительно, то стоит выбирать предел выше. Но чем выше предел, тем больше и времени уйдёт на вычисление точек, потому что их будет больше, это нужно учитывать.
Следует учитывать и производительность вычислительной машины. Я производил вычисления на Процессоре AMD Athlon(tm) II X4 645 с частотой 3.10 ГГц. Нагрузка на Процессор была около 40 % при работе программы. Нагрузки на Память замечено не было.
Алгоритм работает за достаточно хорошее время, но только для относительно не больших значений. Ведь как мы видим по графику 1 и 2, число после 1 миллиарда в большинстве случаев имеет большой разрыв со временем, затраченное на число 494370889, но это было ожидаемо, ведь как было замечено ранее, метод является субэкспоненциальным.
Спасибо, что дочитали мою первую статью.
Использованная литература: “Математические основы защиты информации”
Приведём определение факторизации.
Факторизацией целого числа называется его разложение в произведение простых сомножителей. Такое разложение, согласно основной теореме арифметики, всегда существует и является единственным (с точностью порядка следования множителей).
Будем обозначать число, которое требуется разложить буквой N, а два сомножителя, в результате умножения которых получим N, как a и b.
Алгоритм факторизации Ленстры (факторизация на эллиптических кривых) является одним из самых быстрых методов факторизации. Он имеет много общего с методом Полларда (p – 1), но работает значительно быстрей, следует отметить, что он является субэкспоненциальным методом. Главная особенность алгоритма – это то, что время, затраченное на факторизацию, зависит не от размерности N, а от размера наименьшего делителя числа N.
Подробно про этот метод вы сможете почитать из материала в списке использованной литературы, но всё же приведём основные стадии алгоритма.
- Введём число N.
- Выберем некоторое значение B, которое является максимальным пределом числа-делителя N.
- Сгенерируем случайным образом значения x,y,a, которые принадлежат множеству целых чисел от 0 до N-1. Эти значения определяют кривую, а так же x и y определяют начальную точку P.
- Вычислим b = y^2-x^3-ax mod n и g = Н.О.Д.(N, 4a^3+27b^2). Важно, что бы g не был равен N, иначе возвращаемся к п.2. Если 1 < g < n, тогда прекратим вычисление – делитель найден. Этот вариант возможен при малых значениях числа N (например 10), при возрастании N эта возможность встречается всё реже.
- Далее нужно выполнить цикл, в результате которого для каждого простого числа p (в пределе от 2 до B-1) вычислим точку P, домноженную на p^r, где r наибольшая степень, удовлетворяющая условию p^r < B.
В арифметике полей нет операции деления, которая необходима в формулах для нахождения координат точек, так что мы преобразуем выражение в виде умножения, а обратный элемент ищем по расширенному алгоритму Евклида. К тому же каждое новое вычисление мы производим по модулю числа N.
Алгоритм завершит свою работу, когда будет найден Н.О.Д.(N, P), который больше 1 и меньше N. Во избежание ошибки в ответе, функция нахождения Н.О.Д. должна проверять только положительные значения.
Рассмотрим график времени, которое нам понадобится для факторизации разных чисел. (Результат приведён из написанной мною программы)
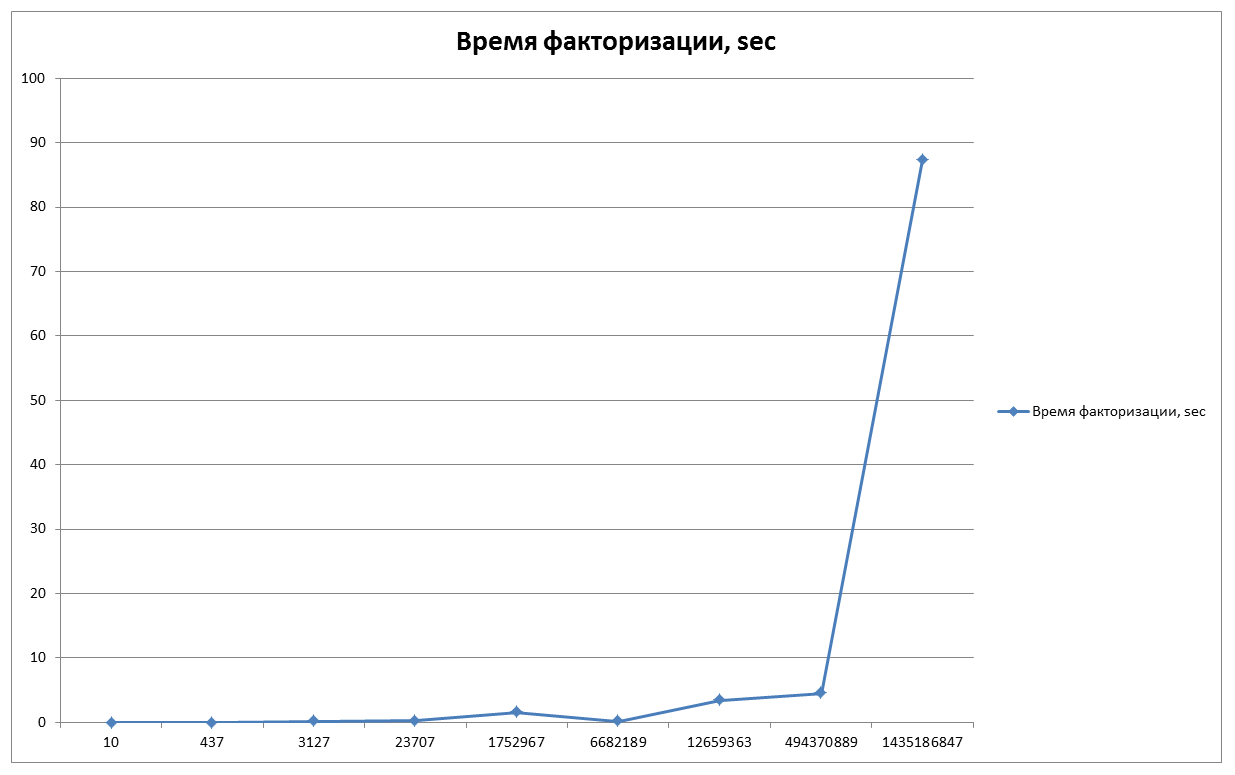
N=10 – 0,005 sec;
N=437 – 0,019 sec;
N=3127 – 0,055 sec;
N=23707 – 0,191 sec;
N=1752967 — 1,534 sec;
N=6682189 — 0,143 sec;
N=12659363 — 3,376 sec;
N=494370889 – 4,484 sec;
N=1435186847 — 87,377 sec;
Так как кривая генерируется из случайных значений, то время факторизации при каждом новом запуске программы будет разным. Смотря удачная ли кривая нам попадётся. По этому, попробуем взять эти же числа и выполнить факторизацию ещё несколько раз и сверим результаты.
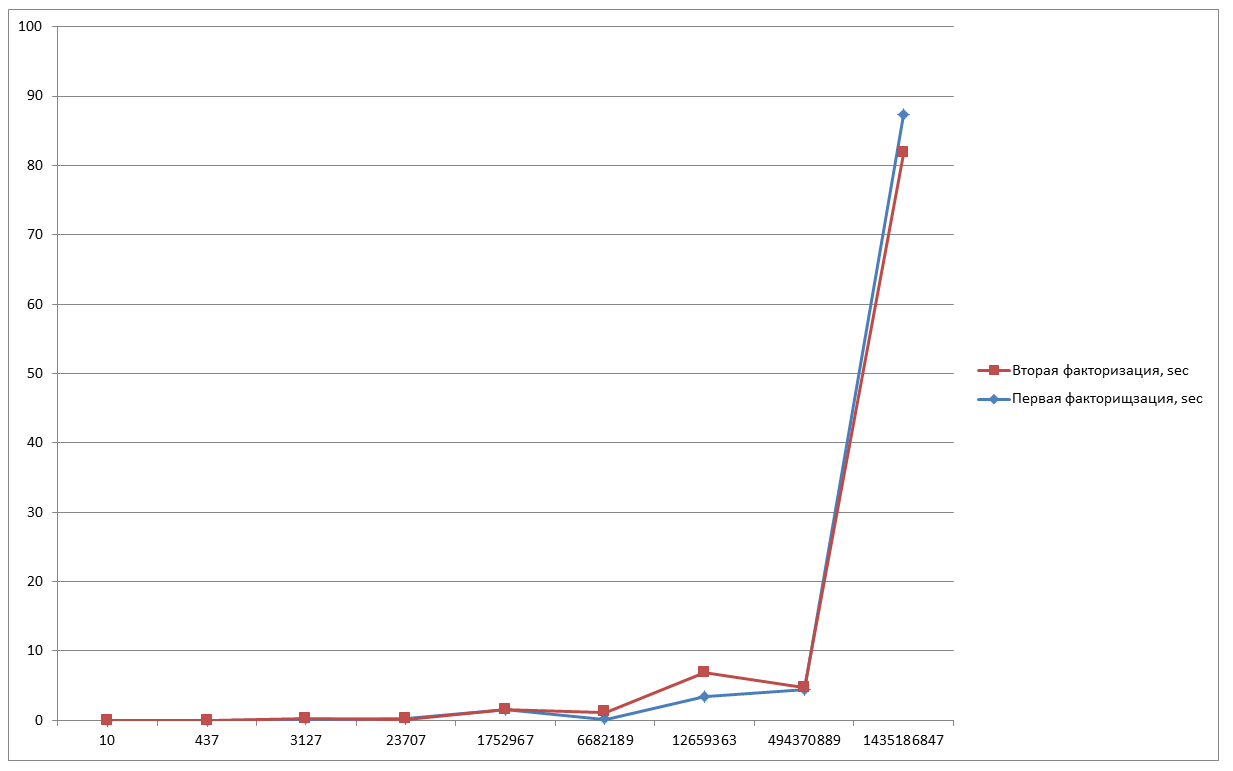
N=10 – 0,016 sec;
N=437 – 0,016 sec;
N=3127 – 0,218 sec;
N=23707 – 0,079 sec;
N=1752967 — 1,484 sec;
N=6682189 — 1,125 sec;
N=12659363 – 6,906 sec;
N=494370889 – 4,781 sec;
N=1435186847 — 81,766 sec;
И для закрепления сделаем последний замер.
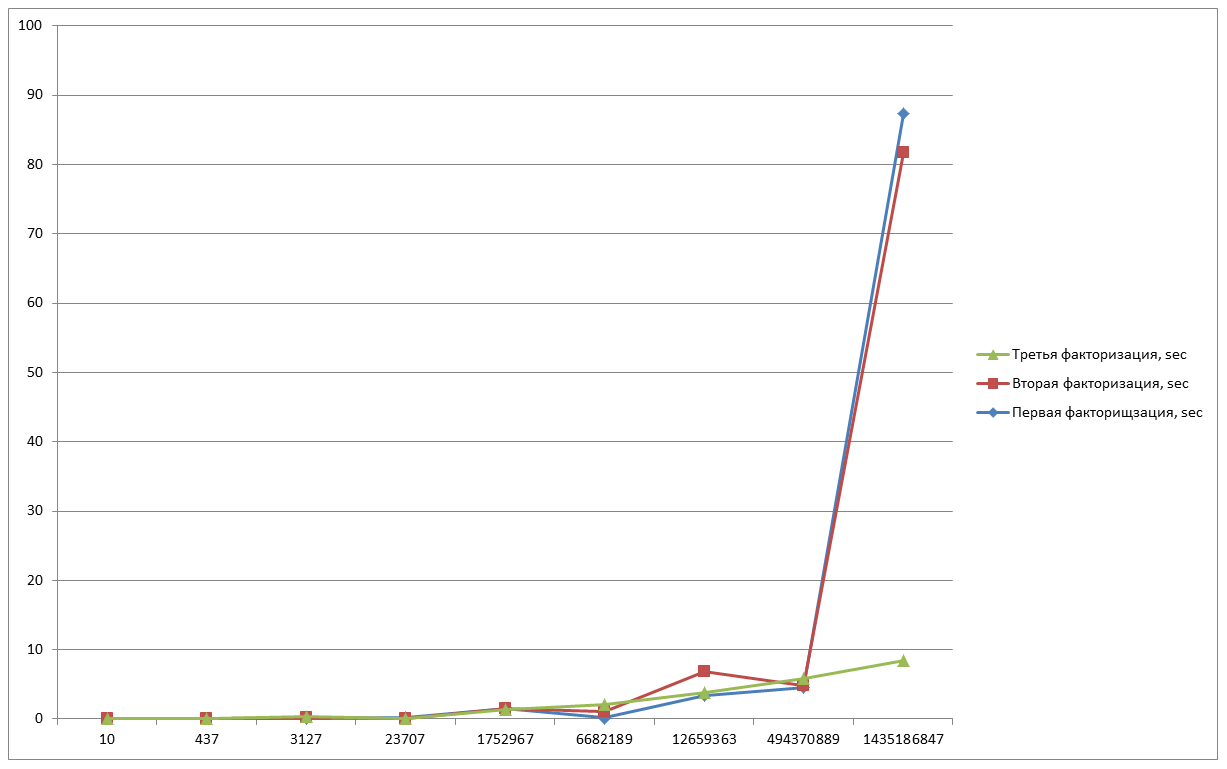
N=10 – 0,012sec;
N=437 – 0,022 sec;
N=3127 – 0,156 sec;
N=23707 – 0,205 sec;
N=1752967 — 1,418 sec;
N=6682189 — 1,056 sec;
N=12659363 – 0,25 sec;
N=494370889 – 5,488 sec;
N=1435186847 – 14,117 sec;
Как мы видим на последнем графике, время затраченное на последнее число заметно уменьшилось, это характеризуется тем, что кривая генерируется случайным образом. Следует заметить, что время, затраченное на выполнение алгоритма, зависит и от значения B, которое мы вводим. Я старался брать значение приближённые к значениям двух сомножителей (a и b), но если вы будете выполнять операцию над числом, где изначальные множители не известны даже приблизительно, то стоит выбирать предел выше. Но чем выше предел, тем больше и времени уйдёт на вычисление точек, потому что их будет больше, это нужно учитывать.
Следует учитывать и производительность вычислительной машины. Я производил вычисления на Процессоре AMD Athlon(tm) II X4 645 с частотой 3.10 ГГц. Нагрузка на Процессор была около 40 % при работе программы. Нагрузки на Память замечено не было.
Итог
Алгоритм работает за достаточно хорошее время, но только для относительно не больших значений. Ведь как мы видим по графику 1 и 2, число после 1 миллиарда в большинстве случаев имеет большой разрыв со временем, затраченное на число 494370889, но это было ожидаемо, ведь как было замечено ранее, метод является субэкспоненциальным.
Спасибо, что дочитали мою первую статью.
Использованная литература: “Математические основы защиты информации”
Поделиться с друзьями
Комментарии (9)
Coocos
09.02.2017 15:55Как оценивали нагрузку на память?
Qwarri
09.02.2017 16:04Я не делал тщательный анализ нагрузки на память, я лишь следил за производительностью и монитором ресурсов в Windows. В общем счёте программа занимает 0,4 МБ памяти в любой момент времени работы. И я сделал вывод, что нагрузки, как таковой, на память нет.
novoxudonoser
09.02.2017 16:59Статья хоть и короткая, но хорошая для первого раза. Но с точки зрения выводов и информативности ниочём.
ShashkovS
10.02.2017 12:44+2Что-то у вас не так с кодом или алгоритмом.
При помощи ро-метода Полларда на питоне:
Число 10 разложено на множители [2, 5] за 0.000020c
Число 437 разложено на множители [19, 23] за 0.000158c
Число 3127 разложено на множители [53, 59] за 0.000099c
Число 23707 разложено на множители [151, 157] за 0.000096c
Число 1752967 разложено на множители [1321, 1327] за 0.000142c
Число 6682189 разложено на множители [2579, 2591] за 0.000267c
Число 12659363 разложено на множители [3557, 3559] за 0.000249c
Число 494370889 разложено на множители [22079, 22391] за 0.000362c
Число 1435186847 разложено на множители [37781, 37987] за 0.000842c
Код на Pythonfrom random import randint from time import perf_counter def gcd(a, b): """НОД(a,b). Считаем, что числа натуральные""" while b: a, b = b, a % b return a def miller_rabin_test(a, n, s, d): """Один тест Миллера-Рабина. Является ли число 2 <= a <= n-2 свидетелем простоты для числа n (n-1 = d * 2**s) Если вдруг среди чисел a**(d*2**0), ..., a**(d*2**s) перед какой-то 1 идёт не -1, то число n — составное, а a — не является свидетелем простоты.""" x = pow(a, d, n) # x = a**(d*2**0) if x in (1, n - 1): return True for r in range(s - 1): x = (x * x) % n # Из числа a**(d*2**r) вычисляем a**(d*2**(r+1)) if x == 1: # Ну всё, число составное return False elif x == n - 1: # Нашлась -1. Число a — свидетель простоты для n return True return False # Даже тест Ферма не пройден: a**(n-1) != 1 def miller_rabin(n): """Проверяет простоту числа n>3, выполняя log2(n) тестов Миллера-Рабина""" # Ищем разложение n-1 = n-1 = d * 2**s s, d = 0, n - 1 while d % 2 == 0: s, d = s + 1, d // 2 for _ in range(n.bit_length()): # Повторяем тест log2(n) раз. a = randint(2, n - 2) # берём случайное число if not miller_rabin_test(a, n, s, d): # Если тест не пройден, то число составное return False return True # С вероятностью 1/n**2 число простое def pollards_rho_iter(n): """Поиск делителя у нечётного составного числа""" # Начинаем с функции F(x) = x**2 + 1 из точки x=2. Обычно это срабатывает x = y = 2 a = 1 while True: d = 1 while d == 1: # Если 1 < d < n, то мы нашли делитель d x = (x * x + a) % n # x = F(F(..(F(x)..)) y = (y * y + a) % n y = (y * y + a) % n # y = F(F(F(F(..(F(F(x))..)))) (в два раз больше раз F) d = gcd(n, abs(x - y)) if d < n: # Если 1 < d < n, то мы нашли делитель d return d # Редко бывает так, что для функции x**2 + 1 при старте с 2 делитель не находится # В этом случае используем F(x) = x**2 + a, и стартуем с другого случайного числа x = y = randint(1, n - 1) a = randint(-100, 100) % n def factor(n): """Факторизация числа при помощи ро-метода Полларда и тестов Миллера-Рабина""" # Избавляемся от всех двоек, троек и пятёрок ans = [] for x in (2, 3, 5): while n % x == 0: ans.append(x) n //= x if n == 1: pass # n = 2**a * 3**b * 5**c elif miller_rabin(n): # Остаток простой ans.append(n) else: # Ищем делители d = pollards_rho_iter(n) ans.extend(factor(d)) ans.extend(factor(n // d)) return sorted(ans) nums = [10, 437, 3127, 23707, 1752967, 6682189, 12659363, 494370889, 1435186847] for num in nums: st = perf_counter() fct = factor(num) en = perf_counter() print('Число {} разложено на множители {} за {:02f}c'.format(num, fct, en-st))sdev
10.02.2017 12:46+1А как вы определили, что что-то не так с кодом, сравнивая при этом с совсем другим алгоритмом?
ShashkovS
10.02.2017 12:50+1Число 19120211505964799 разложено на множители [39916801, 479001599] за 0.028161c
Число 87178204020795979291199 разложено на множители [87178291199, 999999000001] за 1.611496c
Число 126040091637447457926052165206241443360998401 разложено на множители [479001599, 263130836933693530167218012159999999] за 0.427691c
Он имеет много общего с методом Полларда (p – 1), но работает значительно быстрей, следует отметить, что он является субэкспоненциальным методом.
14с в статье против 0.000842c у Полларда (который экспоненциальный, sqrt(мин. делитель))
Отличие по времени на 4 порядка…
sdev
10.02.2017 12:45-1Я правильно понимаю, что в рассчетах все числа укладываются в int? Тоесть к реальному RSA статья не имеет никакого отношения.
saluev
Вы бы хоть программу показали, это же Хабр, а не защита курсовой.
Ну и по-хорошему для анализа эффективности программу нужно запустить не три раза, а три тысячи раз и привести один усреднённый график.
P. S. С недавнего времени Хабр может в формулы.
Qwarri
Спасибо за комментарий, буду стремиться не допускать больше таких недочётов. А что насчёт программы, так у меня были сомнения по поводу нужна ли она здесь, так как это уже отдельная тема.