Сначала пример олимпиадной задачи по логике. На острове живут мудрецы и лжецы. Причем, их да и нет звучат как пиф и паф. Что именно из них что – неизвестно.

Решаем. Мудрец ответит следующим образом: (А = А), (А ? not А). Ответ же лжеца в таком случае: (А ? А), (А = not А). Пусть на их языке пиф – это да. Тогда на вопрос (пиф – это да?) мудрец ответит пиф. Если же на их языке (пиф – это нет), то его ответ будет таким же: пиф. Лжец же всегда будет высказывать несуществующее (то, чего нет), говоря паф.

Итак, конструкция истины (тождественно истинной формулы) А=А, лжи (тождественно ложной формулы) А?А. Эти же формулы позволяют передавать логические примитивы: есть А, нет А. Вот пример на языке python.


Можно выразить все сказанное таким образом:


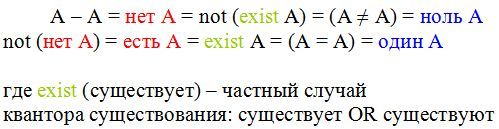
Можно ли пойти дальше, конструируя на этой базе более сложные вещи? Разумеется. Возьмем для примера однозначно замкнутое преобразование Т, в котором в табличном виде представлены переходы (термин кибернетики):

(U: S->Z), (U: Z->S), (U: W->Z), (P: S->Z), (P: Z->W), (P: W->S), (V: S->S), (V: Z->Z), (V: W->Z)


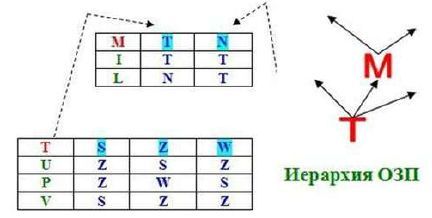
Замечу, что эти переходы отображают тот же смысл, что и морфизмы в теории категорий. Если к аргументу функции применить функцию, то получим только значение функции: (F: X->Y) или (Y=F(X)).

Казалось бы, такое однозначно замкнутое преобразование начисто лишено противоречия (тождественно ложной формулы). Но спросим себя: как тогда интерпретировать, скажем, переход (U: S->Z)? Было S, перестало быть S, возникло Z. Получаем все те же примитивы: есть S, нет S & нет Z, есть Z. Иначе говоря, переменная Т последовательно принимает (говоря только о существующем) значения S, Z.

Можно заметить, что есть (существует) здесь интерпретируется как предикат: (S – есть) или (S — нет). Повторюсь (существует OR существуют), т.е. квантор существования – не то же самое, что (существует). В самом деле, один или более одного – не то же самое, что один.

Применимы ли эти есть и нет к однозначно замкнутым преобразованиям? Да. Так, для однозначно замкнутого преобразования М, одним из состояний является наше T. И выразить его существование и не существование можно также: есть Т = (Т = Т), нет Т = (Т ? Т)