17.07.2017 13:57
Crittografo 29 6900 Источник


Сегодня мы снова поговорим про протокол Диффи-Хеллмана, но уже построенный на более необычных конструкциях — изогениях, которые признаны устойчивыми к атакам на будущем квантовом компьютере. Квантовый компьютер, который сможет удержать в связанном состоянии порядка нескольких тысяч кубит, позволит находить закрытые ключи по открытым ключам у всех используемых сейчас асимметричных криптосистем. Число кубит для взлома RSA равно удвоенному числу бит в модуле (т.е. для разложения на множители модуля RSA длиной 2048 бит потребуется 4096 кубит). Для взлома эллиптических кривых необходимы более скромные мощности «квантового железа»: для решения задачи ECDLP для кривых над простым полем (такие кривые есть и в отечественном стандарте подписи ГОСТ Р 34.10-2012 и в американском ECDSS) c модулем кривой длиной n бит требуется 6n кубит (т. е. для модуля в 256 бит надо ~ 1536 кубит, а для 512 бит ~ 3072 кубит). На днях российско-американская группа ученых установила мировой рекорд, удержав в связанном состоянии 51 кубит. Так что у нас есть еще немного времени для изучения изогений (а также решеток, кодов, multivariate и подписей, основанных на хэшах).
Кстати, изогении считаются одним из наиболее вероятных кандидатов на победу на конкурсе NIST постквантовых алгоритмов для замены RSA и эллиптических кривых в ближайшие несколько лет. Предыдущую статью про прошлое и настоящее Диффи-Хеллмана можно почитать тут .

Что такое изогении?


Отображение, которое переводит точки одной кривой E1 в точки другой кривой E2 (либо в саму себя (тогда считаем E2 = E1)) следующим образом: если на кривой E1 мы выберем любые две точки A1 и B1 и отобразим их в точки A2 и B2 на кривой E2, тогда то же самое отображение обязательно переведет их сумму — точку С1 = A1 + B1 именно в точку С2 = A2 + B2 – сумму их отображений. Это замечательное свойство называется сохранением операции, а такое отображение является гомоморфизмом. Изогению можно выразить с помощью рациональной функции: точка (x, y) отображается в точку с координатами $(\frac{f1(x, y)}{f2(x, y)}, \frac{g1(x, y)}{g2(x, y)})$ (где ${f1, f2, g1, g2}$ – полиномы ).
Если существует такого рода отображение между двумя кривыми, то они называются изогенными. Частный случай изогении — это изогения кривой на саму себя (эндоморфизм).

Каким свойством должны обладать две кривые, чтобы быть изогенными?

Теорема Tate:
Две кривые над одним конечным полем изогенны тогда и только тогда, когда порядки их групп равны.

Пример 1 (изогения кривой на саму себя):

Эндоморфизм: скалярное умножение точки на число: $n*P$ на кривой $y^2 = x^3 + Ax + B$
например, для n = 2 и $P = (x, y)$:

$2*P = (\frac{x^4 - 2Ax^2 - 8Bx - A^2}{4(x^3+Ax+B)}, \frac{(x^6+5Ax^4+20Bx^3-5A^2x^2-4ABx - 8B - A)y}{8(x^3+Ax+B)^2})$

Для произвольного n аналогичная (но более длинная) формула может быть получена рекуррентно при помощи так называемых полиномов деления (division polynomials)

Пример 2 (изогения между разными кривыми):

Пусть есть кривая $E1 : y^2 = x^3+x+1$ над полем $ GF(19) $
и кривая $E2 : y^2 = x^3+4x+13$ над тем же полем.

Порядки групп (т.е. число точек на кривой) у E1 и E2 равны: #E1 = #E1 = 21

По теореме Тейта равенство #E1 = #E1 означает, что между E1 и E2 существует изогения.
j–инвариант E1 = 6, а j–инвариант E2 = 4. Т.е группы точек кривых не изоморфны.
(изоморфизм — это частный случай гомоморфизма, когда каждому элементу в отображении соответствует только один элемент образа (т.е. несколько элементов не переходят в один: отображение только «один в один»))

Изогения, которая отображает точки с E1 на E2 (откуда она взялась мы покажем в Примере 3) может быть представлена с помощью следующего рационального отображения:

Отображение $? : (x, y)$ > $(\frac{x^3-4x^2-8x-8}{x^2-4x+4}, \frac{x^3y-6x^2y+5xy-6y}{x^3-6x^2-7x-8})$

Рассмотрим, к примеру, точки A1 (9, 6) и B1 (14, 2) кривой E1. Их сумма — точка С1 с координатами (5, 6). Если подставить их в формулу выше, то получим их отображение на кривую E2, Соответствующие им точки на E2 — A2, B2, C2:

A1 (9, 6) > A2 (14, 1)
B1 (14, 2) > B2 (17, 4)
C1 (5, 6) > C2 (8, 5)

Легко проверить, что С2 = A2 + B2. Т.е. точка С1 = A1 + B1 переходит в точку С2 = A2 +B2. Если не лень, то можно перебрать все комбинации из любых двух точек E1 A и B и их отображений ?(A) и ?(B) и убедиться, что они ведут себя аналогично:

$?(A + B) = ?(A) + ?(B)$

А что будет, если подставить точки (2, 12) или (2, 7)? Знаменатель правой дроби будет равен нулю! Это всего лишь означает, что эти точки переходят в точку на бесконечности для E2.
Осталось рассмотреть точку на бесконечности на E1. Она «по умолчанию» переходит в точку на бесконечности на E2. Это фундаментальное свойство гомоморфизма: нейтральный элемент (в случае эллиптических кривых — это точка на бесконечности) отображается в нейтральный элемент. Иначе “сломается” сохранение операции для случая, когда один двух элементов – нейтральный.
Степенью изогении называется степень полинома $f1$ в формуле отображения $(\frac{f1(x, y)}{f2(x, y)}, \frac{g1(x, y)}{g2(x, y)})$
В Примере 2 $ f1 = x^3 - 4x^2 - 8x - 8$ Т.е. степень изогении равна 3. Степень означат то, во сколько раз отображение “сжимает” образ. Т.е. 3 разных точки E1 отображаются при такой изогении в одну точку на E2. Множество точек, которые отображаются в точку на бесконечности называются ядром изогении.

Вычисление изогений


Как найти такие отображения? Оказывается, что число возможных изогений для конкретной кривой равно количеству подгрупп в группе ее точек. Существует детерминированный алгоритм который придумал математик Велю (Velu') в 1971 году. Он использует много формул, поэтому сначала покажем его общую схему:

Вход:
кривая $E1: y^2 = x^3 + Ax + B$ и одна из ее подгрупп $C$ (isogeny kernel)

Выход:
кривая $E2: y^2 = x^3 + A'x + B'$, изогенная $E1$ и рациональное отображение $(\frac{f1(x, y)}{f2(x, y)}, \frac{g1(x, y)}{g2(x, y)})$

Сложность алгоритма: $O$(#$C$) шагов, где #$C$ – порядок $C$

Обозначение: $E > E/C$, где $E/C$ кривая, изогенная
$E$, полученная с помощью подгруппы $C$

На выходе мы получаем коэффициенты $A'$ и $B'$ для изогенной кривой и формулу с дробями. Подгруппа С – любая из подгрупп кривой. C является ядром изогении: все ее элементы переходят в точку на бесконечности. Если кривая E1 изогенна кривой E2, то верно и обратное: E2 изогенна E1: существует гомоморфное отображение и в обратную сторону.

А теперь объясним, зачем мы все это нагромоздили (и будем дальше это делать):
также, как для мультипликативных групп конечного поля и эллиптических кривых, для изогении существует своя сложная задача, которую можно (и нужно) использовать для создания ЭЦП и аналогов Диффи-Хеллмана.

Сложная задача для изогений:
Даны две изогенные кривые $E1$ и $E2$ с различными j- инвариантами. Требуется найти изогению между ними.

Если мы имеем две кривые, про которые мы знаем, что они изогенные (а это так, если равны порядки их групп), но не знаем при помощи какой подгруппы можно получить эту изогению. Очевидно, что число подгрупп должно быть большим настолько, чтобы было вычислительно сложно найти изогению простым перебором, подставляя подгруппы в алгоритм Velu'.

Алгоритм Velu':

Вход:
кривая $E1: x^3 + Ax + B$ и одна из ее подгрупп $C$ (ядро изогении)

1. Отбрасываем точку на бесконечности
2. Находим $C_2$ — множество точек четного порядка из $C$.
$R$ — все остальные
3. Разбиваем $R$ на две части — $R_{+}$ и $R_{-}$: если точка P – в $R_{+}$, то обратная ей – в $R_{-}$
4. Множество $S = C_2 ? R_{+}$

Для каждой точки $Q = (x_Q, y_Q)$ из $S$

$g_{Q}^x = 3x_{Q}^2 + A$
$g_{Q}^y = -2y_{Q}$

$if (Q = -Q)$
$v_{Q} = g_{Q}^x$
$else$
$v_{Q} = 2g_{Q}^x$

$u_{Q} = (g_{Q}^y)^2$

$v = \sum_{Q ? S}(v_{Q})$
$w = \sum_{Q ? S}(u_{Q} + x_{Q}v_{Q})$

Коэффициенты $A'$ и $B'$ для уравнения изогенной кривой $ E' $:
$ A' = A - 5v $
$ B' = B - 7w $

Итак, изогенную кривую мы знаем. Как вычислить отображение $(x, y)$ > $(?, ?) $:

$? = x + \sum_{Q ? S}(\frac{v_Q}{(x-x_Q)} + \frac{u_Q}{(x-x_Q)^2})$
$? = y - \sum_{Q ? S}(u_Q\frac{2y}{(x-x_Q)^3} + v_Q \frac{y - y_Q}{(x-x_Q)^2} - \frac{g_Q^xg_Q^y}{(x-x_Q)^2})$

Выход алгоритма Velu':
Коэффициенты $A'$, $B'$ изогенной кривой и формула для отображения точек $(x, y)$ > $(?, ?)$

Пример 3 (Алгоритм Velu'. Как была получена изогения в Примере 2):

Вход :
$y^2 = x^3+x+1$ над полем $GF(19)$ и подгруппа $C$: { $O$, $(2, 7)$, $(2, 12)$ }

1. Отбрасываем точку на бесконечности
2. Точек четного порядка нет в $C$ нет
3. Выбираем для $R_{+}$ точку $(2, 7)$. Точка $(2, 12)$ – ей обратна ( т.к.7 = -12 mod 19 )
4. Множество $S$ = { $(2, 7)$ }

Цикл из одного шага: (т.к. в $S$ только один элемент: точка $Q = (2, 7) $):

$Q = (2, 7)$, ее координаты $ x_Q = 2, y_Q = 7$
$g_Q^x = 3*2^2 + 1 = 13$
$g_Q^y = -2*7 = -14 = 5$ $ mod $ $ 19 $
$v_Q = 2*13 = 26$ $ mod $ $ 19 = 7 $
$u_Q = 5^2$ $ mod $ $ 19 = 6 $
$v = 7$
$w = 6 + 2*7 = 20 = 1$ $ mod $ $ 19 $
$A' = A - 5v= 1 – 5*7 = - 34$ $ mod $ $ 19 $ = $4$
$B' = B - 7w = 13$

Осталось только посчитать рациональное отображение: $ (x, y) > (?, ?)$:
$? = x + \frac{7}{x-2} + \frac{6}{(x-2)^2} = \frac{x^3-4x^2-8x-8}{x^2-4x+4}$

Аналогично приводим формулу для ? к общему знаменателю:
$? = \frac{x^3y-6x^2y+5xy-6y}{x^3-6x^2-7x-8}$

Выход:
Коэффициенты изогенной кривой: $A' = 4, B' = 13$
Отображение $(x, y) > (?, ?)$ (см. выше).

Вычисление изогений большой степени


Легко видеть, что в алгоритме Velu имеются подводные камни: он работает в цикле, пока не пройдется по всем точкам из множества $S$. Это значит, что число шагов будет больше половины порядка ядра изогении (подгруппы $C$, которая подается на вход) и меньше порядка $C$. Velu может использовать только относительно маленькие подгруппы, чтобы можно было в приемлемое время пройти все шаги алгоритма, что осложняет криптографическое применение изогений. К счастью есть метод, который позволяет быстро вычислять изогении, даже если группа $C$ имеет большой порядок #$C$, но имеет определенную структуру: если #$C$ — степень небольшого числа $l$, т.е. $l^e$. В таком случае алгоритм состоит из e шагов, на каждом из которых считается изогения степени $l$ по Velu' и одно скалярное умножение точки на число. В качестве $l$ обычно выбирают 2 или 3.

Обозначение: Кривую $E'$, изогенную $E$, полученную при помощи подгруппы $C$, вместо $E$/$C$, иногда гораздо удобнее обозначать при помощи точки $G$ — генератора $C$: $E/<$ $G$ $>$.

Пусть $G$ — точка порядка $l^e$. Необходимо вычислить изогению $?: E > E/<$ $G$ $>$.
Разложим изогению $?$ на последовательность из изогений, где каждая имеет степень $l$ $?_{e-1}*?_{e-2}*...*?_{0}$:
$?_0 : E, G_0 = G$
$?_i : E_{i+1} = E_i/<$ $l^{e-1-i}G_i$ $>$ ,$G_{i+1} = ?_i( G_i )$

Пример 4
Мы хотим вычислить изогению для циклической группы порядка $l^4$
Вместо того, чтобы один раз применить алгоритм Velu' для группы применим его 4 раза, каждый раз считая изогению степени $l$ и 3 раза умножим точку на число. Пусть $G_0$ — генератор этой группы, точка порядка $l^4$.

$?_{3}$*$?_{2}$*$?_{1}$*$?_{0}$:

$?_0 : E_1 = E_0/<$ $l^{3}*G_0$ $>$, $G_1 = ?_0(G_0)$

$?_1 : E_2 = E_1/<$ $l^{2}*G_1$ $>$, $G_2 = ?_1(G_1) $

$?_2 : E_3 = E_2/<$ $l^{1}*G_2$ $>$, $G_3 = ?_2(G_2)$

$?_3 : E_4 = E_3/<$ $G_3$ $>$

Итак, теперь мы умеем вычислять изогении для циклических групп очень большого порядка. К примеру, если есть группа порядка $2^{256}$ и мы знаем ее генератор, то мы пройдем алгоритм за 256 шагов.

Практика: изогении между суперсингулярными кривыми


Напомним, что у двух изоморфных кривых одинаковый j-инвариант и для кривой $y^2 = x^3 + Ax + B$ он равен $1728\frac{4A^3}{4A^3+27B^2}$
Из за того, что найти преобразование между изоморфными кривыми особой сложности не представляет, задача изогений по сути является задачей про нахождение изогений между различными классами изоморфных кривых (а каждый из этих классов можно представить в виде соответствующего j-инварианта).
Какие кривые представляют интерес для изогений? Ведь мы знаем, что существуют запрещенные семейства кривых для эллиптических Диффи-Хеллмана и ЭЦП: суперсингулярные, аномальные и гладкого порядка и.т.д. — для всех относительно легко решается задача ECDLP. Такие неприятные классы должны существовать и для изогений. Только тут ситуация совершенно иная, ведь трудная задача не ECDLP. Очевидно, что надо использовать кривые гладкого порядка, чтобы было больше подгрупп. Кроме того, в 2010 году исследователи из университета Ватерлоо выяснили, что использование обычных кривых небезопасно с «квантовой» точки зрения: был получен результат, который утверждал, что для криптосистем, использующих изогении безопасно использовать только суперсингулярные кривые. Напомним, что это кривые, у которых след Фробениуса t такой что t mod p = 0, где p — характеристика поля кривой (сам след Фробениуса связан с порядком группы кривой #$E(GF(p^n))$ и полем соотношением #$E(GF(p^n)) = p^n + 1 - t)$. Далее мы будем рассматривать только их.

Какое поле для кривой оптимальнее было бы использовать? Сразу напрашивается ответ — старое доброе простое поле $GF(p)$. Но к сожалению, у суперсингулярных кривых над $GF(p)$ существует слишком мало разных j-инвариантов: ~ $\sqrt{p}$. Тогда как для поля $GF(p^2)$, число j-инвариантов #$S_{p^2} = \lfloor p/12 \rfloor + a$, где $a ? ${$1, 2, 3 $}

У таких кривых есть интересные свойства:
Граф изогений фиксированной степени — правильный. (т.е у каждой вершины имеется одинаковое число ребер)
Для любого простого числа $l$, которое делит порядок группы точек кривой существует $l+1$ изогений с ядром порядка $l$. (т.е. существует $l+1$ подгруппа порядка $l$, при помощи которой можно получить изогению)

Пример 5 (пример и изображения графов — Dr. Fre Vercauteren)
Рассмотрим поле $GF({241^2})$
Выберем неприводимый многочлен: $x^2 - 3x +7$
Множество j-инвариантов будет таким:
$S_{241^2}$ = { 93, 51w + 30, 190w + 183, 240, 216, 45w + 211, 196w +
105, 64, 155w + 3, 74w + 50, 86w + 227, 167w + 31, 175w + 237, 66w + 39, 8, 23w + 193, 218w + 21, 28, 49w + 112, 192w + 18 }
Их число #$S_{241^2}$ = 20

Для кривых порядка #$E$ = 57600 = $2^8*3^2*5^2$:

Для изогении степени $ l = 2$:
Каждая кривая имеет 3 изогении степени 2


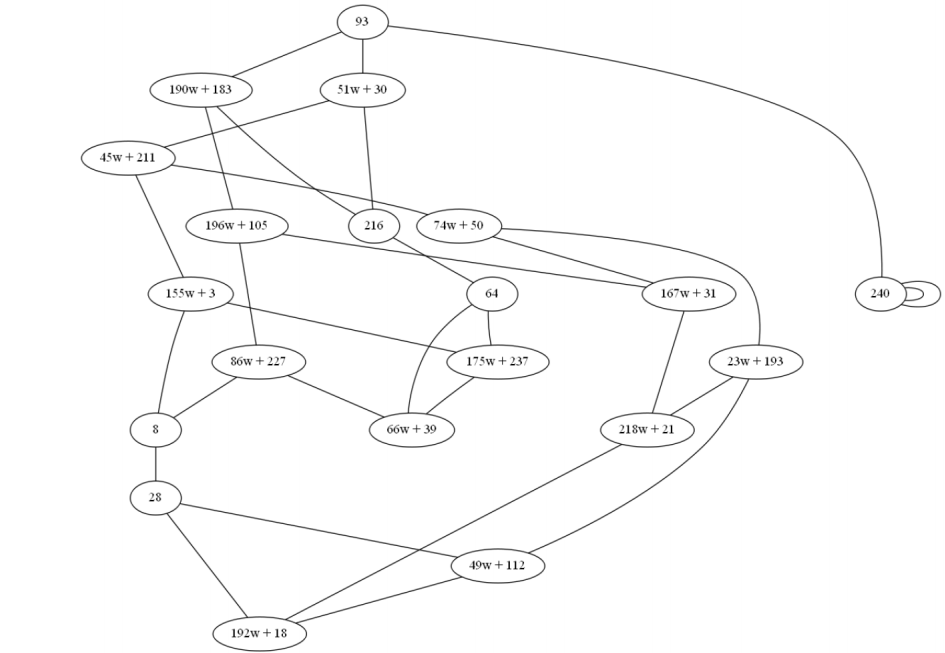
Для изогении степени $l = 3$:
Каждая кривая имеет 4 изогении степени 3


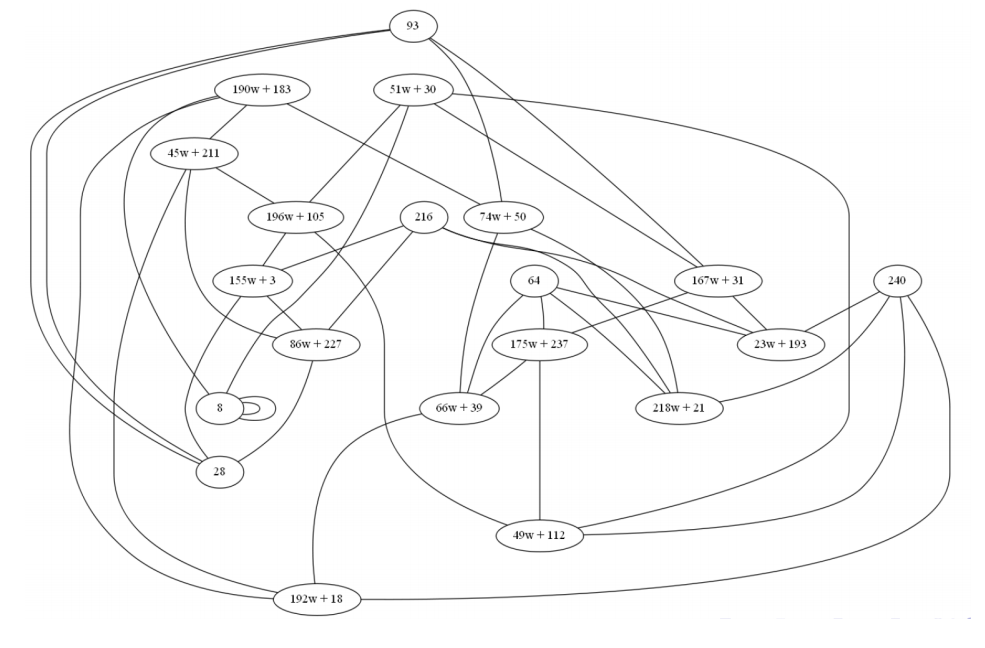
Аналогично для $l = 11$.
Каждая кривая имеет 12 изогении степени 11.

Сложную задачу, которую придется решать злоумышленнику, теперь можно сформулировать так: зная две кривые $E1$ и $E2$ (т.е. зная два $j$-инварианта $j1$ и $j2$), найти путь в графе изогений между ними. По сути — найти метод получения изогении между кривой c $j1$ и кривой c $j2$

Supersingular Isogeny Diffie-Hellman (SIDH)


Определение:
Если при умножении точки $P$ кривой $E(GF(p^m))$ при умножении на n получается точка на бесконечности, то такая точка называется точкой n-кручения (n-torsion point)
Подгруппа n-кручения (n-torsion subgroup) $ E[n] $:
$E[n] =${$P ? E(GF(p^m)) : n*P = O$}
Эта подгруппа состоит из точки на бесконечности и всех точек n-кручения.
Очевидно, что точкой n-кручения является точка, если ее порядок делит n без остатка.

$E[n]$ изоморфна прямому произведению $(Z/nZ)?(Z/nZ)$ при n взаимно простом с p. (т.е порядок $E[n]$ равен $n^2$ )

Выбор поля $GF(p^2)$ для кривых для SIDH:
Пусть $f$ — небольшое число, а $l_a, l_b$ — небольшие простые числа.
При характеристике поля $p = l_a^{e_a}*l_b^{e_b}*f±1$ порядок кривой $E$: #$E = (l^{e_a}*l^{e_b}*f)^2$
$E[l^{e_a}]$ содержит $l_a^{e_a - 1}(l_a+1)$ циклических подгрупп порядка $l_a^{e_a}$

Итак, пусть $l_a = 2, l_b = 3$
характеристика поля $p = 2^{m}*3^{n}*f±1$, а n и m подберем так, чтобы $2^{m}$ приблизительно было равно $3^{n}$
Подгруппы кручения $E[2^m]$ и $E[3^n]$ ? $E[p^2]$

$E[2^m]$ содержит $2^{m?1}*3$ циклических подгрупп порядка $2^m$
$E[3^n]$ содержит $3^{n?1}*4$ циклических подгрупп порядка $3^n$

Выберем точки $P_a, Q_a$ — базис для $E[2^m]$ (т.е. при помощи комбинации $ x*P_a + y*Q_a$ можно получить любую точку $E[2^m]$) и точки $P_b, Q_b$ — базис для $E[3^n]$

Итак доменные параметры для SIDH (аналог доменных параметров для обычных эллиптических кривых):
кривая $E$ и два базиса {$P_a, Q_a$} и {$P_b, Q_b$}. Они известны Алисе, Бобу и злоумышленнику.


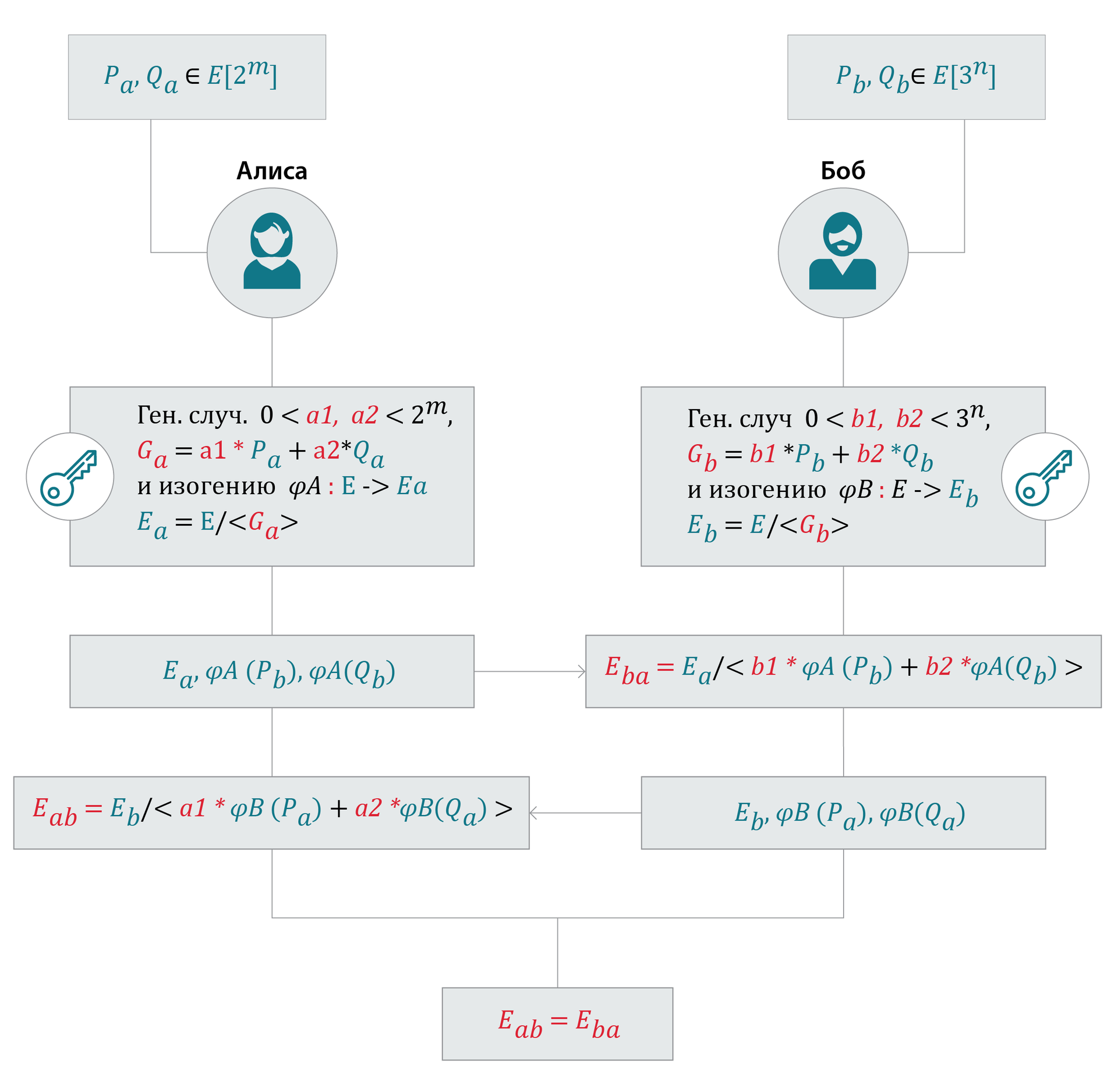
(Примечание: $E_{ab} = E_{ba}$ c точностью до изоморфизма: коэффициенты у кривых могут быть разные, но j-инвариант будет одинаковый)

Тот, кто начинает (Алиса) использует для генерации пары базис $P_a, Q_a$.
Алиса генерирует случайные $a1, a2: 0< a1, a2 < 2^m$ ($a1, a2$ оба не кратны 2)
$a1, a2$ — это закрытый ключ Алисы.
Затем она вычисляет вычисляет точку $G_a = a1*P_a + a2*Q_a$
И вычисляет с ее помощью изогению $?A:$ $E > E_a = E$ /< $G_a$ >,
после чего преобразует c помощью изогении $?A$ базис Боба на кривую $E_a $: $?A({P_b}), ?A({Q_b})$

Закрытый ключ Алисы: $a1, a2$
Открытый ключ Алисы: кривая $ E_a$ и точки $?A({P_b}), ?A({Q_b})$

Аналогичные шаги делает Боб (см. диаграмму):
Закрытый ключ Боба: $b1, b2$
Открытый ключ Боба: кривая $E_b$ и точки $?B({P_a}), ?B({Q_a})$

Алиса отправляет открытый ключ Бобу
Боб вычисляет точку $b1*?A({P_b}) + b2*?A({Q_b})$ и с ее помощью
изогенную кривую $E_{ba} = E_a$/<$b1*?A({P_b}) + 2*?A({Q_b})$>

Далее, Боб отправляет Алисе открытый ключ и Алиса подобным образом вычисляет кривую $E_{ab}:$
$E_{ab} = E_b$/<$a1*?B({P_a}) + a2*?B({Q_a})$>

Для получения общего секрета Алиса вычисляет j-инвариант от $E_{ab}$
а Боб от $E_{ba}$.

Безопасность и размеры ключей


Для успешной атаки надо найти путь хотя бы на одном из графов (Алисы или Боба). Эта задача имеет разные степени сложности для классического и квантовых компьютеров:
Классическая сложность: Алиса $\sqrt{2^m} $, Боб $\sqrt{3^n}$
Квантовая сложность: Алиса $ \sqrt[3]{2^m} $, Боб $\sqrt[3]{3^n}$
Поэтому:
Классический уровень безопасности = $min (\sqrt{2^m}, \sqrt{3^n} ) ? \sqrt[4]{p}$ операций
Квантовый уровень безопасности = $min ( \sqrt[3]{2^m}, \sqrt[3]{3^n} ) ? \sqrt[6]{p}$ операций

Размеры ключей:

Открытый ключ:
точки P и Q
коэффициенты A и B кривой

~ 8 * $log_2(p)$ бит
~ 6 * $log_2(p)$ бит (оптимизация: Costello, Crypto 2016 )

Длина характеристики поля = 768 бит:
768/6 = 128-битный квантовый уровень безопасности
768/4 = 192-битный классический уровень безопасности
Длина ключа 6 $log_2(p)$ бит = 4608 бит = 576 байт

Длина характеристики поля = 1536 бит:
1536/6 = 256-битный квантовый уровень безопасности
1536/4 = 384-битный классический уровень безопасности
Длина ключа 6 $log_2(p)$ бит = 9216 бит = 1152 байт

Производительность


Лучшие результаты для 128-битного квантового уровня безопасности (характеристика поля $p = 2^{372}3^{239} - 1$ т.е $p$ ~ $2^{768}$):

Для Intel Haswell на частоте 3,4 Ггц:
вычисляется за ~100 млн. тактов для одной из сторон (Алисы или Боба)
(используются кривые Монтгомери и проективные координаты)

Для чипа ARM7 Beagle Board Black Cortex-A8 на частоте 1 Ггц:
время выполнения — 1,5 сек. Если задействовать SIMD-инструкции NEON, то 0,2 сек.

Литература:


1. «Public-Key Cryptosystem Based on Isogenies», Alexander Rostovtsev, Anton Stolbunov, 2006

2. «Constructing elliptic curve isogenies in quantum subexponential time» Andrew M. Childs, David Jao, Vladimir Soukharev, 2010

3. «Towards Quantum-Resistant Cryptosystems from Supersingular Elliptic Curve Isogenies» David Jao, Luca De Feo, 2011

4. «Efficient algorithms for supersingular isogeny Diffie-Hellman» Craig Costello and Patrick Longa and Michael Naehrig, 2016

5. «NEON-SIDH: Efficient implementation of supersingular isogeny Diffie-Hellman Key Exchange protocol on ARM» R. Azarderaksh, D. Jao, 2016

6. «Mathematics of Public Key Cryptography» Steven D. Galbraith, Cambridge University Press
Поделиться с друзьями
-->

Комментарии (29)


  1. r85qPZ1d3y
    17.07.2017 22:17
    #10316294
    +2

    Все очень понятно, и написано доступным языком. Спасибо.


    1. igordata
      18.07.2017 08:20
      #10316538
      +5

      С таким-то ником может и понятно. А остальным как быть? =(


    1. Crittografo
      18.07.2017 14:22
      #10317128
      +1

      Пожалуйста! Рад, что вам понравилась статья. Видимо не зря старался :)


  1. msin
    17.07.2017 23:31
    #10316344

    Есть планы по реализации этого алгоритма в ключах Sign и Code?
    И вообще планы по развитию аппаратной и программной части ключей Guardant


    1. Crittografo
      19.07.2017 02:34
      #10318298

      Михаил, я написал вам в личные сообщения


  1. MetromDouble
    17.07.2017 23:31
    #10316346
    +1

    Благодарю, замечательный и отлично структурированный материал. Осталось только его понять. Когда-нибудь.


  1. amarao
    18.07.2017 13:38
    #10317020

    Что такое порядок группы для кривой? (из фразы) «Две кривые над одним конечным полем изогенны тогда и только тогда, когда порядки их групп равны.».


    1. Crittografo
      18.07.2017 14:04
      #10317094

      Порядок группы — это число ее элементов. Порядок группы точек кривой — число элементов группы точек кривой.
      Но можно сказать еще проще: это число всех точек на конкретной кривой + одна точка на бесконечности. Вы можете посмотреть мою предыдущую статью


      1. amarao
        18.07.2017 15:58
        #10317394
        -1

        Что такое «группа точек кривой» и чем она отличается от «все точки кривой»? Если «группа точек» — это все точки, то можем ли мы говорить, что группа точек на синусоиде и на параболе сравнимая — и там и там бесконечность?

        Я посмотрел вашу предыдущую статью и она так же слишком переполнена словами, которые средний айтишник (к которым я отношу себя) не знает.


        1. mayorovp
          18.07.2017 17:10
          #10317546

          Группа — это множество, на котором определена некоторая обратимая ассоциативная бинарная операция. Если на пальцах, то можно сказать что группа — это когда можно умножать и делить.


          Например, целые числа образуют группу по сложению, то же самое можно сказать про вещественные или рациональные числа.


          Без ноля те же самые множества образуют группу по умножению.


          Более подробно об этом можно почитать в Википедии


          1. amarao
            18.07.2017 17:18
            #10317558

            Окей, тогда, получается, что группа точек кривой, это такой набор точек, для которых есть условное умножение и сложение.

            Теперь мы говорим про порядок группы. У нас есть две непрерывные гладкие функции определённые на всём множестве вещественных чисел. Будет ли порядок группы точек первой кривой отличаться от порядка группы второй кривой?

            А если одна кривая определена на отрезке вещественных чисел? Например, равны ли порядки для групп точек кривой x2+y2=1 и кривой y=sin(x)?


            1. mayorovp
              18.07.2017 17:31
              #10317578

              Нет, только умножение. Если операций две — то это уже поле (или кольцо, если вторая операция необратима).


              Обратите внимание также на формулировку теоремы Tate:


              Две кривые над одним конечным полем изогенны тогда и только тогда, когда порядки их групп равны.

              Кривая над конечным полем никак не может содержать бесконечное количество точек :-)


              1. amarao
                18.07.2017 17:58
                #10317644

                (Я читаю вашу статью по слогам. В смысле, до первого непонятного предложения)

                Ага, всё сложнее. У нас рядом с «группой» появляется слово «поле». Группа — это когда определена операция умножения, поле — когда определены умножение и сложение.

                Конечное поле означает, что у нас сами кривые — это всего лишь множество точек, это не «бесконечная гладкая всюду дифференцируемая» кривая из матанализа.

                Пытаюсь развернуть определение «теоремы Tate»: Кривая — конечное множество точек на поле, описываемое какой-то функцией. Для поля определены операции умножения и сложения. Для точек кривой как минимум определено умножение и деление.

                Мы говорим, что две такие кривые изогенны, тогда и только тогда, когда содержат одинаковое количество точек, так?

                Раскрывая определение изогенности:

                Если кривые заданы над множеством точек, для которых определено умножение, деление и сложение, то тогда и только тогда, если у кривых одинаковое количество точек, то:

                Существует такая функция, отображающая точки первой кривой в точки второй кривой, которая для двух любых точек первой кривой, отобразит их сумму на первой кривой в сумму отображений точек на второй кривой.

                Переводя на компьютерный язык:

                Если у нас есть тип данных с конечным числом значений (enum или int), для которого определены операции сложения, умножения и деления, то для любых двух одинаковых по длине массивов элементов этого типа, мы можем создать такую функцию, что она будет отображать все элементы первого массива во второй массив, причём так, что для любой пары элементов из первого массива мы сможем отобразить их в такие элементы второго массива, что сумма значений выбранной пары элементов первого массива равна сумме элементов второго массива.

                У меня есть некоторое ощущение, что в районе «поля» задаются какие-то ещё ограничения, которые я не понял.

                Допустим, у меня есть поле [1,2,3,4,5,6]. На этом поле у меня определены операции сложения (для некоторых элементов), умножения (аналогично), деления (аналогично).

                1) Является ли 1-6 полем? Мне кажется, что нет. Если таки да, то:
                Допустим, у меня есть кривая [1,2,3] и и [4,5,6]. Есть ли такое отображение, которое будет давать изогенное отображение? Как оно выглядит?

                Если я где-то сделал фатальную ошибку, объясните мне её, пожалуйста. И если это возможно, проиллюстрируйте на конечном множестве чисел как оно должно быть. Спасибо.


                1. Crittografo
                  18.07.2017 18:06
                  #10317662

                  Объясните пожалуйста, что такое поле [1,2,3,4,5,6]? вы не забыли про 0? :)


                  1. amarao
                    18.07.2017 18:38
                    #10317734

                    Я его не забыл, я про него не знал. Видимо, поле должно обладать какими-то специальными свойствами.

                    Интересно, если у меня есть беззнаковая арифметика по модулю 256, то это будет полем?

                    Мне как айтишнику будет очень легко смотреть на математические операции над байтом.


                    1. Crittografo
                      18.07.2017 19:13
                      #10317802

                      Нет, не будет. По модулю 257 будет.


                    1. mayorovp
                      18.07.2017 19:22
                      #10317818

                      Беззнаковая арифметика по модулю 256 — это не поле, а кольцо. Разница — в обратимости умножения. Например, нельзя разделить 1 на 2 нацело.


                      Тем не менее, с 256 элементами поле построить можно — это будет поле двоичных полиномов, порожденное полиномом 8й степени. Именно в таком поле производит вычисления, к примеру, алгоритм CRC-8 (вообще, все семейство алгоритмов CRC основано на полях двоичных полиномов, порожденных полиномами соответствующих степеней). Роль сложения в таких полях играет операция XOR (побитовое исключающее "или").


                      1. Crittografo
                        18.07.2017 19:44
                        #10317854

                        Если вам интересны конечные поля и вам нужны примеры, чтобы разобраться, то рекомендую установить open-source пакет SAGE — он много чего умеет. А кроме того, я бы почитал классику: «Конечные поля» Лиддла и Нидеррайтера или еще лучше «Алгебра» Глухова


                1. Crittografo
                  18.07.2017 18:21
                  #10317692

                  Допустим, что у вас есть конечное поле из p^n элементов.(все конечные поля имеют такой порядок)
                  Вы не можете взять и поделить его на две одинаковые части, поскольку каждая из них по отдельности не будет полем.


                  1. amarao
                    18.07.2017 18:37
                    #10317728

                    А можно увидеть пример двух кривых, которые построены на базе какого-то поля, причём так, чтобы размерность кривой (число точек) было меньше, чем число элементов поля?


                    1. Crittografo
                      18.07.2017 19:07
                      #10317784

                      Да, конечно :)

                      Elliptic Curve defined by y^2 = x^3 + 1 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 2 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 3 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 7 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 11 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 14 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + x + 2 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + x + 5 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + x + 6 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + x + 7 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + x + 10 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + x + 11 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 6 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 8 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 10 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 12 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 14 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 15 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 17 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 2*x + 18 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 6 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 8 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 10 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 12 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 14 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 15 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 17 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 3*x + 18 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 1 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 3 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 7 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 9 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 15 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 4*x + 17 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 1 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 4 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 11 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 13 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 14 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 5*x + 16 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 1 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 3 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 7 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 9 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 15 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 6*x + 17 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 2 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 5 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 6 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 7 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 10 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 7*x + 11 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 2 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 8 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 9 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 12 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 13 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 15 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 16 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 8*x + 18 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 1 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 3 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 7 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 9 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 15 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 9*x + 17 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 3 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 4 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 5 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 8 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 10 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 12 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 13 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 10*x + 18 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 2 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 5 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 6 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 7 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 10 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 11*x + 11 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 2 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 8 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 9 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 12 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 13 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 15 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 16 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 12*x + 18 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 3 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 4 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 5 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 8 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 10 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 12 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 13 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 13*x + 18 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 6 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 8 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 10 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 12 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 14 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 15 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 17 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 14*x + 18 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 3 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 4 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 5 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 8 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 10 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 12 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 13 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 15*x + 18 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 1 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 4 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 11 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 13 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 14 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 16*x + 16 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 1 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 4 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 11 over Finite Field of size 19
                      has order
                      18
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 13 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 14 over Finite Field of size 19
                      has order
                      12
                      Elliptic Curve defined by y^2 = x^3 + 17*x + 16 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 2 over Finite Field of size 19
                      has order
                      14
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 8 over Finite Field of size 19
                      has order
                      13
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 9 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 12 over Finite Field of size 19
                      has order
                      15
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 13 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 15 over Finite Field of size 19
                      has order
                      17
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 16 over Finite Field of size 19
                      has order
                      16
                      Elliptic Curve defined by y^2 = x^3 + 18*x + 18 over Finite Field of size 19
                      has order
                      18


                  1. Crittografo
                    18.07.2017 18:43
                    #10317740

                    где p — это простое число. Но даже если p = 2 и число элементов получится 2^n, то все равно вам придется взять в одну из двух частей 0 или 1 и они уже не будут полями.


                1. mayorovp
                  18.07.2017 19:14
                  #10317804

                  Это не моя статья. Поля из шести элементов существовать не может, из-за того что не получается выдержать обратимость умножения.


        1. Crittografo
          18.07.2017 17:56
          #10317638

          «Все точки кривой» — это множество всех точек кривой. Понятие «группа точек кривой» предполагает наличие операции между любыми двумя точками, результат которой — точка той же самой кривой. Эта операция должна удовлетворять определенным правилам, которые одинаковы для всех групп (мультипликативная группа, которая используется в классическом Диффи-Хеллмане также этим правилам удовлетворяет (иначе она называлась бы не группа)). Вот эти правила: 1. ассоциативность (a*b)*c = a*(b*c) 2. в группе всегда есть нейтральный элемент e такой, что a*e = e*a = a (для любого a). 3. для любого элемента x в группе существует обратный элемент y: x*y = y*x = e
          При написании статьи всегда возникает вопрос: насколько далеко стоит уходить в описание элементарных понятий. Ведь можно сделать статью либо недоступной к пониманию, либо просто скучной. Ее главная цель — вызвать интерес к предмету, даже если что-то не совсем понятно. В любом случае большое спасибо за сигнал — я добавлю определений в первую статью.


          1. amarao
            18.07.2017 17:59
            #10317650

            Я не могу говорить за всех, но мне бы хотелось иметь возможность понять написанное с скудным багажом из матанализа и хорошим представлением об обычных типах данных.

            Другими словами, если бы все понятия иллюстрировались примером на конкретных компьютерных типах данных, то это бы сильно помогло понять их.


            1. Crittografo
              18.07.2017 18:25
              #10317702

              Да не вопрос, сегодня-завтра добавлю материал про группы и поле с примерами.


              1. amarao
                18.07.2017 18:39
                #10317736

                Если можно, то с обязательными простыми (обозримыми) примерами. Понять из примера по индукции как оно будет на больших масштабах проще, чем по общему правилу придумать себе самому правильный пример.


  1. mkirya
    18.07.2017 14:21
    #10317126

    В Safari тег math не срабатывает


    1. Crittografo
      19.07.2017 01:57
      #10318270

      Исправил — вроде теперь видно.