Введение и постановка задачи
На 3-м курсе обучения в своем университете передо мной встала задача реализовать B-дерево, содержащее уникальные ключи, упорядоченное по возрастанию (со степенью t=2) на языке c++ (с возможностью добавления, удаления, поиска элементов и соответственно, перестройкой дерева).
Перечитав несколько статей на Хабре (например, B-tree, 2-3-дерево. Наивная реализация и другие), казалось бы, все было ясно. Только теоретически, а не практически. Но и с этими трудностями мне удалось справиться. Цель моего поста — поделиться полученным опытом с пользователями.
Немного основных моментов
B-деревом называется дерево, удовлетворяющее следующим свойствам:
1. Каждый узел содержит хотя бы один ключ. Корень содержит от 1 до 2t-1 ключей. Любой другой узел содержит от t-1 до 2t-1 ключей. Листья не являются исключением из этого правила. Здесь t — параметр дерева, не меньший 2.
2. У листьев потомков нет. Любой другой узел, содержащий n ключей, содержит n+1 потомков. При этом:
а) Первый потомок и все его потомки содержат ключи из интервала
б) Для
в) (n+1)-й потомок и все его потомки содержат ключи из интервала
3. Глубина всех листьев одинакова.
Реализация
Для начала создадим структуру узла нашего дерева.
const int t=2;
struct BNode {
int keys[2*t];
BNode *children[2*t+1];
BNode *parent;
int count; //количество ключей
int countSons; //количество сыновей
bool leaf;
};Теперь создадим класс Tree, включающий в себя соответствующие методы.
class Tree {
private:
BNode *root;
void insert_to_node(int key, BNode *node);
void sort(BNode *node);
void restruct(BNode *node);
void deletenode(BNode *node);
bool searchKey(int key, BNode *node);
void remove(int key, BNode *node);
void removeFromNode(int key, BNode *node);
void removeLeaf(int key, BNode *node);
void lconnect(BNode *node, BNode *othernode);
void rconnect(BNode *node, BNode *othernode);
void repair(BNode *node);
public:
Tree();
~Tree();
void insert(int key);
bool search(int key);
void remove(int key);
};Сразу описываем конструктор и деструктор. В деструкторе вызывается рекурсивный метод удаления элементов из дерева.
Tree::Tree() { root=nullptr; }
Tree::~Tree(){ if(root!=nullptr) deletenode(root); }
void Tree::deletenode(BNode *node){
if (node!=nullptr){
for (int i=0; i<=(2*t-1); i++){
if (node->children[i]!=nullptr) deletenode(node->children[i]);
else {
delete(node);
break;
}
}
}
}Первым делом рассмотрим добавление ключа в узел. В моем случае (t=2) это будет выглядеть следующим образом:
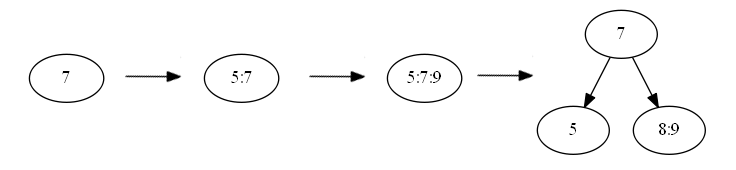
Т.е., как только в узле становится больше 3 элементов — узел разбивается.
Итак, для добавления элемента в дерево необходимо реализовать несколько методов.
Первый – простое добавление в узел. В данном методе вызывается метод сортировки, необходимый для выполнения условия о возрастающих значениях дерева. Второй метод –
добавления значения в узел, в котором предварительно ищется нужная позиция и при
необходимости (в узле становится больше 3 элементов) вызывается третий метод – метод разбиения узла на: родителя и двух сыновей.
Первый метод – метод простого добавления.
void Tree::insert_to_node(int key, BNode *node){
node->keys[node->count]=key;
node->count=node->count+1;
sort(node);
}Метод сортировки чисел в узле:
void Tree::sort(BNode *node) {
int m;
for (int i=0; i<(2*t-1); i++){
for (int j=i+1; j<=(2*t-1); j++){
if ((node->keys[i]!=0) && (node->keys[j]!=0)){
if ((node->keys[i]) > (node->keys[j])){
m=node->keys[i];
node->keys[i]=node->keys[j];
node->keys[j]=m;
}
} else break;
}
}
}Думаю, тут всё понятно.
Второй метод – метод добавления значения в узел с предварительным поиском позиции:
void Tree::insert(int key){
if (root==nullptr) {
BNode *newRoot = new BNode;
newRoot->keys[0]=key;
for(int j=1; j<=(2*t-1); j++) newRoot->keys[j]=0;
for (int i=0; i<=(2*t); i++) newRoot->children[i]=nullptr;
newRoot->count=1;
newRoot->countSons=0;
newRoot->leaf=true;
newRoot->parent=nullptr;
root=newRoot;
} else {
BNode *ptr=root;
while (ptr->leaf==false){ //выбор ребенка до тех пор, пока узел не будет являться листом
for (int i=0; i<=(2*t-1); i++){ //перебираем все ключи
if (ptr->keys[i]!=0) {
if (key<ptr->keys[i]) {
ptr=ptr->children[i];
break;
}
if ((ptr->keys[i+1]==0)&&(key>ptr->keys[i])) {
ptr=ptr->children[i+1]; //перенаправляем к самому последнему ребенку, если цикл не "сломался"
break;
}
} else break;
}
}
insert_to_node(key, ptr);
while (ptr->count==2*t){
if (ptr==root){
restruct(ptr);
break;
} else {
restruct(ptr);
ptr=ptr->parent;
}
}
}
}Третий метод – метод разбиения узла:
void Tree::restruct(BNode *node){
if (node->count<(2*t-1)) return;
//первый сын
BNode *child1 = new BNode;
int j;
for (j=0; j<=t-2; j++) child1->keys[j]=node->keys[j];
for (j=t-1; j<=(2*t-1); j++) child1->keys[j]=0;
child1->count=t-1; //количество ключей в узле
if(node->countSons!=0){
for (int i=0; i<=(t-1); i++){
child1->children[i]=node->children[i];
child1->children[i]->parent=child1;
}
for (int i=t; i<=(2*t); i++) child1->children[i]=nullptr;
child1->leaf=false;
child1->countSons=t-1; //количество сыновей
} else {
child1->leaf=true;
child1->countSons=0;
for (int i=0; i<=(2*t); i++) child1->children[i]=nullptr;
}
//второй сын
BNode *child2 = new BNode;
for (int j=0; j<=(t-1); j++) child2->keys[j]=node->keys[j+t];
for (j=t; j<=(2*t-1); j++) child2->keys[j]=0;
child2->count=t; //количество ключей в узле
if(node->countSons!=0) {
for (int i=0; i<=(t); i++){
child2->children[i]=node->children[i+t];
child2->children[i]->parent=child2;
}
for (int i=t+1; i<=(2*t); i++) child2->children[i]=nullptr;
child2->leaf=false;
child2->countSons=t; //количество сыновей
} else {
child2->leaf=true;
child2->countSons=0;
for (int i=0; i<=(2*t); i++) child2->children[i]=nullptr;
}
//родитель
if (node->parent==nullptr){ //если родителя нет, то это корень
node->keys[0]=node->keys[t-1];
for(int j=1; j<=(2*t-1); j++) node->keys[j]=0;
node->children[0]=child1;
node->children[1]=child2;
for(int i=2; i<=(2*t); i++) node->children[i]=nullptr;
node->parent=nullptr;
node->leaf=false;
node->count=1;
node->countSons=2;
child1->parent=node;
child2->parent=node;
} else {
insert_to_node(node->keys[t-1], node->parent);
for (int i=0; i<=(2*t); i++){
if (node->parent->children[i]==node) node->parent->children[i]=nullptr;
}
for (int i=0; i<=(2*t); i++){
if (node->parent->children[i]==nullptr) {
for (int j=(2*t); j>(i+1); j--) node->parent->children[j]=node->parent->children[j-1];
node->parent->children[i+1]=child2;
node->parent->children[i]=child1;
break;
}
}
child1->parent=node->parent;
child2->parent=node->parent;
node->parent->leaf=false;
delete node;
}
}Для поиска были реализованы следующие методы, возвращающие true или false (второй метод рекурсивный):
bool Tree::search(int key){
return searchKey(key, this->root);
}
bool Tree::searchKey(int key, BNode *node){
if (node!=nullptr){
if (node->leaf==false){
int i;
for (i=0; i<=(2*t-1); i++){
if (node->keys[i]!=0) {
if(key==node->keys[i]) return true;
if ((key<node->keys[i])){
return searchKey(key, node->children[i]);
break;
}
} else break;
}
return searchKey(key, node->children[i]);
} else {
for(int j=0; j<=(2*t-1); j++)
if (key==node->keys[j]) return true;
return false;
}
} else return false;
}Реализация метода удаления ключа из узла была самой сложной. Ведь в некоторых случаях удаления нужно склеивать соседние узлы, а в некоторых брать значения из узлов «братьев». Например:
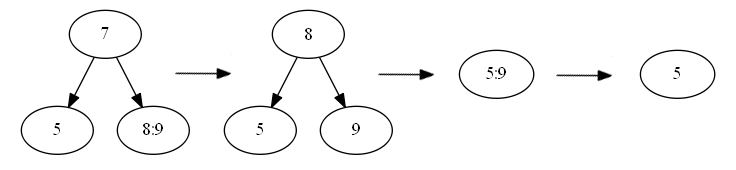
Удаление представляет собой несколько случаев. Первый из них — простой метод удаления ключа из узла:
void Tree::removeFromNode(int key, BNode *node){
for (int i=0; i<node->count; i++){
if (node->keys[i]==key){
for (int j=i; j<node->count; j++) {
node->keys[j]=node->keys[j+1];
node->children[j]=node->children[j+1];
}
node->keys[node->count-1]=0;
node->children[node->count-1]=node->children[node->count];
node->children[node->count]=nullptr;
break;
}
}
node->count--;
}Во втором же случае после удаления ключа необходимо соединить соседние узлы. Поэтому второй и третий методы – методы соединения узлов:
void Tree::lconnect(BNode *node, BNode *othernode){
if (node==nullptr) return;
for (int i=0; i<=(othernode->count-1); i++){
node->keys[node->count]=othernode->keys[i];
node->children[node->count]=othernode->children[i];
node->count=node->count+1;
}
node->children[node->count]=othernode->children[othernode->count];
for (int j=0; j<=node->count; j++){
if (node->children[j]==nullptr) break;
node->children[j]->parent=node;
}
delete othernode;
}
void Tree::rconnect(BNode *node, BNode *othernode){
if (node==nullptr) return;
for (int i=0; i<=(othernode->count-1); i++){
node->keys[node->count]=othernode->keys[i];
node->children[node->count+1]=othernode->children[i+1];
node->count=node->count+1;
}
for (int j=0; j<=node->count; j++){
if (node->children[j]==nullptr) break;
node->children[j]->parent=node;
}
delete othernode;
}Четвертый метод – метод «починки» узла. В данном методе дерево в буквальном смысле перестраивается до тех пор, пока не будут удовлетворены все условия B-дерева:
void Tree::repair(BNode *node){
if ((node==root)&&(node->count==0)){
if (root->children[0]!=nullptr){
root->children[0]->parent=nullptr;
root=root->children[0];
} else {
delete root;
}
return;
}
BNode *ptr=node;
int k1;
int k2;
int positionSon;
BNode *parent=ptr->parent;
for (int j=0; j<=parent->count; j++){
if (parent->children[j]==ptr){
positionSon=j; //позиция узла по отношению к родителю
break;
}
}
//если ptr-первый ребенок (самый левый)
if (positionSon==0){
insert_to_node(parent->keys[positionSon], ptr);
lconnect(ptr, parent->children[positionSon+1]);
parent->children[positionSon+1]=ptr;
parent->children[positionSon]=nullptr;
removeFromNode(parent->keys[positionSon], parent);
if(ptr->count==2*t){
while (ptr->count==2*t){
if (ptr==root){
restruct(ptr);
break;
} else {
restruct(ptr);
ptr=ptr->parent;
}
}
} else
if (parent->count<=(t-2)) repair(parent);
} else {
//если ptr-последний ребенок (самый правый)
if (positionSon==parent->count){
insert_to_node(parent->keys[positionSon-1], parent->children[positionSon-1]);
lconnect(parent->children[positionSon-1], ptr);
parent->children[positionSon]=parent->children[positionSon-1];
parent->children[positionSon-1]=nullptr;
removeFromNode(parent->keys[positionSon-1], parent);
BNode *temp=parent->children[positionSon];
if(ptr->count==2*t){
while (temp->count==2*t){
if (temp==root){
restruct(temp);
break;
} else {
restruct(temp);
temp=temp->parent;
}
}
} else
if (parent->count<=(t-2)) repair(parent);
} else { //если ptr имеет братьев справа и слева
insert_to_node(parent->keys[positionSon], ptr);
lconnect(ptr, parent->children[positionSon+1]);
parent->children[positionSon+1]=ptr;
parent->children[positionSon]=nullptr;
removeFromNode(parent->keys[positionSon], parent);
if(ptr->count==2*t){
while (ptr->count==2*t){
if (ptr==root){
restruct(ptr);
break;
} else {
restruct(ptr);
ptr=ptr->parent;
}
}
} else
if (parent->count<=(t-2)) repair(parent);
}
}
}Пятый метод – метод удаления ключа из листа:
void Tree::removeLeaf(int key, BNode *node){
if ((node==root)&&(node->count==1)){
removeFromNode(key, node);
root->children[0]=nullptr;
delete root;
root=nullptr;
return;
}
if (node==root) {
removeFromNode(key, node);
return;
}
if (node->count>(t-1)) {
removeFromNode(key, node);
return;
}
BNode *ptr=node;
int k1;
int k2;
int position;
int positionSon;
int i;
for (int i=0; i<=node->count-1; i++){
if (key==node->keys[i]) {
position=i; //позиция ключа в узле
break;
}
}
BNode *parent=ptr->parent;
for (int j=0; j<=parent->count; j++){
if (parent->children[j]==ptr){
positionSon=j; //позиция узла по отношению к родителю
break;
}
}
//если ptr-первый ребенок (самый левый)
if (positionSon==0){
if (parent->children[positionSon+1]->count>(t-1)){ //если у правого брата больше, чем t-1 ключей
k1=parent->children[positionSon+1]->keys[0]; //k1 - минимальный ключ правого брата
k2=parent->keys[positionSon]; //k2 - ключ родителя, больше, чем удаляемый, и меньше, чем k1
insert_to_node(k2, ptr);
removeFromNode(key, ptr);
parent->keys[positionSon]=k1; //меняем местами k1 и k2
removeFromNode(k1, parent->children[positionSon+1]); //удаляем k1 из правого брата
} else { //если у правого <u>единственного</u> брата не больше t-1 ключей
removeFromNode(key, ptr);
if (ptr->count<=(t-2)) repair(ptr);
}
} else {
//если ptr-последний ребенок (самый правый)
if (positionSon==parent->count){
//если у левого брата больше, чем t-1 ключей
if (parent->children[positionSon-1]->count>(t-1)){
BNode *temp=parent->children[positionSon-1];
k1=temp->keys[temp->count-1]; //k1 - максимальный ключ левого брата
k2=parent->keys[positionSon-1]; //k2 - ключ родителя, меньше, чем удаляемый и больше, чем k1
insert_to_node(k2, ptr);
removeFromNode(key, ptr);
parent->keys[positionSon-1]=k1;
removeFromNode(k1, temp);
} else { //если у <u>единственного</u> левого брата не больше t-1 ключей
removeFromNode(key, ptr);
if (ptr->count<=(t-2)) repair(ptr);
}
} else { //если ptr имеет братьев справа и слева
//если у правого брата больше, чем t-1 ключей
if (parent->children[positionSon+1]->count>(t-1)){
k1=parent->children[positionSon+1]->keys[0]; //k1 - минимальный ключ правого брата
k2=parent->keys[positionSon]; //k2 - ключ родителя, больше, чем удаляемый и меньше, чем k1
insert_to_node(k2, ptr);
removeFromNode(key, ptr);
parent->keys[positionSon]=k1; //меняем местами k1 и k2
removeFromNode(k1, parent->children[positionSon+1]); //удаляем k1 из правого брата
} else {
//если у левого брата больше, чем t-1 ключей
if (parent->children[positionSon-1]->count>(t-1)){
BNode *temp=parent->children[positionSon-1];
k1=temp->keys[temp->count-1]; //k1 - максимальный ключ левого брата
k2=parent->keys[positionSon-1]; //k2 - ключ родителя, меньше, чем удаляемый и больше, чем k1
insert_to_node(k2, ptr);
removeFromNode(key, ptr);
parent->keys[positionSon-1]=k1;
removeFromNode(k1, temp);
} else { //если у обоих братьев не больше t-1 ключей
removeFromNode(key, ptr);
if (ptr->count<=(t-2)) repair(ptr);
}
}
}
}
}Шестой метод – метод удаления из произвольного узла:
void Tree::remove(int key, BNode *node){
BNode *ptr=node;
int position; //номер ключа
int i;
for (int i=0; i<=node->count-1; i++){
if (key==node->keys[i]) {
position=i;
break;
}
}
int positionSon; //номер сына по отношению к родителю
if (ptr->parent!=nullptr){
for(int i=0; i<=ptr->parent->count; i++){
if (ptr->children[i]==ptr){
positionSon==i;
break;
}
}
}
//находим наименьший ключ правого поддерева
ptr=ptr->children[position+1];
int newkey=ptr->keys[0];
while (ptr->leaf==false) ptr=ptr->children[0];
//если ключей в найденном листе не больше 1 - ищем наибольший ключ в левом поддереве
//иначе - просто заменяем key на новый ключ, удаляем новый ключ из листа
if (ptr->count>(t-1)) {
newkey=ptr->keys[0];
removeFromNode(newkey, ptr);
node->keys[position]=newkey;
} else {
ptr=node;
//ищем наибольший ключ в левом поддереве
ptr=ptr->children[position];
newkey=ptr->keys[ptr->count-1];
while (ptr->leaf==false) ptr=ptr->children[ptr->count];
newkey=ptr->keys[ptr->count-1];
node->keys[position]=newkey;
if (ptr->count>(t-1)) removeFromNode(newkey, ptr);
else {
//если ключей не больше, чем t-1 - перестраиваем
removeLeaf(newkey, ptr);
}
}
}И седьмой метод – сам метод удаления, принимающий в качестве входных данных — значение ключа для удаления из дерева.
void Tree::remove(int key){
BNode *ptr=this->root;
int position;
int positionSon;
int i;
if (searchKey(key, ptr)==false) {
return;
} else {
//ищем узел, в котором находится ключ для удаления
for (i=0; i<=ptr->count-1; i++){
if (ptr->keys[i]!=0) {
if(key==ptr->keys[i]) {
position=i;
break;
} else {
if ((key<ptr->keys[i])){
ptr=ptr->children[i];
positionSon=i;
i=-1;
} else {
if (i==(ptr->count-1)) {
ptr=ptr->children[i+1];
positionSon=i+1;
i=-1;
}
}
}
} else break;
}
}
if (ptr->leaf==true) {
if (ptr->count>(t-1)) removeFromNode(key,ptr);
else removeLeaf(key, ptr);
} else remove(key, ptr);
}Вот, как-то так. Надеюсь, кому-то статья будет полезной. Спасибо за внимание.
Комментарии (32)

knstqq
10.09.2017 20:38+5Не понятно зачем нужно и «bool leaf;», и метод «is_leaf()», лучше назвать по разному, если у них разное назначение, либо от одного избавиться.
В C++ дурной тон писать NULL. Либо 0, либо nullptr, как появилось в новом C++11.
Непонятно что с exception-safety, дерево в неконсистентное состояние придёт, если один из new бросит исключение, например.
Метод search() как и другие нужно сделать константными, const, noexcept и другие модификаторы очень важны. Во-первых, константные методы должны быть константными, чтобы не нужно было читать имплементацию для уверенности этого, во-вторых, компилятор генерирует более эффективный код в среднем, в-третьих, из-за одного пропущенного const приходится в десятках мест использующий ваш код множить mutable, const_cast'ы или пропускать const в множестве кода вокруг. Плохой стиль в общем.
Вот эта часть совсем не C++, а C77:
int i; for (i=0; i<=(node->count-1); i++){
Кучи лишних проверок на нулевой указатель, например здесь:if(root!=NULL) deletenode(root);
Ну и код. Огромные куски кода. Статья стала бы действительно хорошей, если бы вы совместили теорию и под спойлеры спрятали куски кода + ссылка на GitHub с полным проектом, а так… Плюс в карму, минус за статью, в целом лабораторная работа — хорошая.

Tantrido
10.09.2017 20:44unordered_map? Я тоже когда-то лет 15 назад такой велосипед изобретал, когда в STL ещё не было реализации.

daiver19
10.09.2017 22:10to:Tantrido (ошибся веткой)
WAT? В-дерево, как и прочие деревья поиска, работают за log n и имеют упорядоченную структуру, т.е. полная противоположность unordered_map aka хэш-таблицы.
Tantrido
10.09.2017 23:37Простите: std::map :
Maps are typically implemented as binary search trees.
www.cplusplus.com/reference/map/mapBHYCHIK
10.09.2017 23:43А оно подходит для внешней памяти?) Сомневаюсь.

Tantrido
10.09.2017 23:45А при чём тут внешняя память? В постановке задачи это было?
BHYCHIK
11.09.2017 00:04Ну как бы B-дерево для внешней памяти прежде всего используют.
kmu1990
11.09.2017 01:26+11. прежде всего, не значит всегда, b-tree очень успешно используется и для работы в оперативной памяти;
2. реализация в статье не работает с внешней памятью и вообще никаким образом не упоминает внешнюю память;
3. реализация в статье даже если бы работала с внешней памятью была бы не сильно эффективнее обычного бинарного дерева, потому что t = 2.

Videoman
11.09.2017 00:19Такое многообразие существующих структур данных, которые вы, почему-то, смешали в одну кучу, существует именно из-за того, что каждая из них более эффективна и применима в своем конкретном случае:
unordered_map — хеш-таблица, амортизированный доступ O(1), элементы не упорядочены
map — двоичное дерево, амортизированный доступ O(logN), элементы упорядочены, упор на скорость доступа в памяти
b-tree — N-ричное сильноветвящееся дерево, амортизированный доступ O(logN), элементы упорядочены, упор на скорость доступа на блочном устройстве хранения (т.е. количество узлов до листа 3-4, но узлы большие и хранят сразу много элементов)kmu1990
11.09.2017 01:331. вы мешаете в кучу амортизированные оценки и средние оценки, а это не одно и тоже;
2. двоичных деревьев поиска есть много разных и не все из них дают «амортизированный доступ» за O(log N), но вы их почему-то смешли в одну кучую;
3. ну и map — это стандартный контейнер C++, от него требуются определенные гарантии, но использование двоичного дерева поиска в качестве реализации не является одной из этих гарантий.
Videoman
11.09.2017 09:32двоичных деревьев поиска есть много разных и не все из них дают «амортизированный доступ» за O(log N), но вы их почему-то смешли в одну кучую
Я в курсе про двоичные деревья, и я комментировал ответ, там понятно о чем речь. На мой взгляд, логично предположить что любое, практичное, двоичное сбалансированное дерево будет иметь сложность основных операции O(logN), а не O(N^2).
ну и map — это стандартный контейнер C++, от него требуются определенные гарантии, но использование двоичного дерева поиска в качестве реализации не является одной из этих гарантий
Я в курсе про стандарт и мне не хотелось бы уходить в такие дебри. Опять же, де факто, используется красно-черные двоичные деревья, которые, по факту, 2-3-4 деревья. Используются для экономии в реализации по памяти, т.к. нужен всего один дополнительный бит на узел.
С чем вы спорите мне не понятно.kmu1990
11.09.2017 11:04+1Я вам тонко намекают, что вы зря критикует человека за то что он что-то там смешал, во первых потому что он ничего не смешивали, а как вы выразились "не стал уходить в дебри", а во вторых потому что вы сами много чего намешали в кучу.
И кстати придумать бинарное дерево поиска в котором базовые операции работают за квадрат, а не за линию, это нужно немного постараться.

Videoman
11.09.2017 16:39По поводу замечаний про деревья я с вашими замечаниями согласен и в курсе, что на самом деле все намного сложней. Теперь, в рамках обсуждения b-tree, Tantrido упомянул сначала unordered_map (очевидно, по названию, что в контексте С++), потом поправился на map. Я, всего-лишь, хотел уточнить что b-tree другая структура и используется, как правило, с внешней памятью, т.к. по скорости поиска в памяти, где прыжки по случайным адресам, относительно внешних носителей, дешевы, уступает двоичному дереву.
kmu1990
11.09.2017 17:03+1Вот просто так берет и уступает? Безотносительно нагрузки? А как насчёт кеш локальности и TLB локальности?

Videoman
11.09.2017 17:11Смотря какие операции и кокой N в узлах. Если только поиск, то может и не уступает. А вот балансировка и вставка будет сложнее. Если брать все операции, в общем, то разработчики stl посчитали что уступает.
kmu1990
11.09.2017 17:56А может быть разработчикам STL нужно было соблюдать семантику итераторов описанную в стандарте и поэтому они решили использовать бинарное дерево поиска с которым проще этого добиться, а скорость и затраты памяти тут не причём? Может вы не будете выставлять свои гадания как подтвержденные факты?

Videoman
11.09.2017 18:20Ну давайте не будем считать разработчиков STL идиотами. Кстати, итераторы не лучшая из концепций, во всяком случае, в том виде как она реализована в STL, но, исходя из эффективности, разработчики пошли на компромисс между скоростью, удобством и безопасностью. В STL стандартизована куча интерфейсов, реализация которых не описана, но почти напрямую из них вытекает, именно потому, что об эффективности думали не в последнюю очередь. Не вижу проблем реализовать итераторы в AVL-tree или в B-Tree. Нет, вы всерьез считаете что сначала появился стандарт, а потом уже думали как его эффективно реализовать на С++?

encyclopedist
11.09.2017 18:30Стандарт закладывался в 90-е годы, 20-25 лет назад. Тогда действительно случайный доступ к памяти можно было считать условно-мгновенным и эффектами локальности кэша пренебречь. С тех пор многое изменилось. Вы можете сами попробовать: возьмите stx-btree или cpp-btree и сравните с std::map. На многих задачах превосходство оказывается очень серьезным.

Videoman
11.09.2017 18:44Я нигде не утверждал и не спорю что нельзя сделать эффективнее в конкретном случае, но для повседневных задач, где и планировалось использовать STL, его скорости, вполне хватает. std::map действительно не очень шустрый, в основном из-за new, да и памяти жрет многовато. Но если в конкретном месте нужна сверхэффективность, то там STL никто не будет использовать и стандартный new тоже, согласитесь?

encyclopedist
11.09.2017 18:55Я к тому, что если раньше B-tree считался дисковой структурой данных, то теперь он более эффективен чем черно-красные деревья и в оперативной памяти.
RAM is the new disk
kmu1990
11.09.2017 18:53Вы не видите проблемы, а я вижу. Для b-tree можно реализовать итераторы, но если соблюдать все требования итераторов std::map, толку от такой реализации будет не много.
И да, то что создатели C++ не определили семантику std::map и его итераторов так, чтобы её можно было эффективно реализовать используя b-tree не делает их идиотами, но это и не делает b-tree медленнее бинарного дерева поиска и не делает ваши гадания фактами.

Videoman
11.09.2017 19:39Еще раз, я не утверждаю, что нельзя эффективнее сделать. Я знаю что B-Tree на современном железе быстрее из-за последовательного доступа и минимизации использования new. Но мы, вроде, обсуждали STL и стандартные контейнеры, и в рамках STL B-tree реализовать можно (собственно красно-черное дерево, которое обычно используется там и есть 2-3-4 дерево, которое есть частный случай B-tree, и итераторы там работают), но будет не эффективно.
kmu1990
11.09.2017 19:55+1Вы не утверждали? А я вот читаю ваши комментарии и вижу обратное.
Нет мы обсуждали не стандартные контейнеры, а то что вы смешали кучу всего в кучу (при этом обвинив в этом кого-то другого), затем мы обсуждали ваше утверждение о том, что бинарные деревня поиска при работе в памяти быстрее чем b-tree (сильное утверждение без всяких оговорок, но, если и может быть), а затем мы обсуждали создателей STL и то какие они не дураки...

Videoman
11.09.2017 23:40Нет, мы обсуждали не стандартные контейнеры
Такое ощущение, что вас было много и я вклинился не в тему. Давайте вы не будете за других решать что им обсуждать, а что нет. Обсуждать B-tree в отрыве от конкретики, как вы это предлагаете мне не интересно.
Интересно обсудить почему в стандарте контейнеры реализованы так, а не иначе и почему не используется B-tree. Вашу точку зрения я понял. Вы педалируете идею что B-tree, чуть ли не, серебряная пуля и пора уже заменить все деревья на B-Tree. Я с вами не согласен. Кеш и локальность играет тем большее значение, чем тип хранимого значения ближе к POD. Даже если бы возможно было изменить интерфейс, то в библиотеке общего плана, такой как STL, невозможно полагаться что большинство объектов в таком дереве будет «плоскими» и иметь быстрые компараторы. При большом количестве элементов в узле (а иначе какая может быть локальность) в b-tree вам придется линейно пробегаться и вызывать большое число компараторов, возможно, не «линейных» объектов, которые вы не контролируете. В двоичном дереве за одно сравнение вы сразу отсекаете половину элементов. Выигрыш от кеша и локальности вы получите только при быстрых компараторах, если это возможно и POD-like элементах, на что в общем случае полагаться невозможно. Именно по этой причине разработчики и и меняют реализацию дерева в std::map, а не потому что они ретрограды и 25 лет ковыряются в носу. Чем сложнее объекты, тем больше нивелируется влияние кеша и тем больше выигрывает двоичное дерево у B-tree.kmu1990
12.09.2017 00:10Давайте вы не будете за других решать что им обсуждать, а что нет.
Я ничего за других не решаю, а вам бы стоило перечитать свои же комментарии.
Вы педалируете идею что B-tree, чуть ли не, серебряная пуля и пора уже заменить все деревья на B-Tree.
Да ну? Покажите пожалуйста, где я такое утверждал?
в b-tree вам придется линейно пробегаться и вызывать большое число компараторов
А про бинарный поиск вы не слышали?
В двоичном дереве за одно сравнение вы сразу отсекаете половину элементов.
А в B-tree нет?
Выигрыш от кеша и локальности вы получите только при быстрых компараторах, если это возможно и POD-like элементах, на что в общем случае полагаться невозможно.
Вы пишете ерунду, из того, что на кеш и TLB локальность в общем случае нельзя полагаться никак не следует, что нужно их всегда игнорировать. И перед тем как делать такие сильные утверждения возьмите и потестируйте разные алгоритмы.
Videoman
12.09.2017 00:54Да ну? Покажите пожалуйста, где я такое утверждал?
Вот же.А про бинарный поиск вы не слышали?
Опа, а как же ваш «любимый» кеш? Бинарный поиск с O(logN) разве не эквивалентен бинарному дереву?
А в B-tree нет?
Элементов в узле то больше. Чуть выше вы же говорили про бинарный поиск.
Вы пишете ерунду.
Это не я пишу ерунду, а вы используете подростковую категоричность не желая слушать другую точку зрения. Почитайте любую книгу по теории структур данных и вы узнаете что любое дерево, в том числе и B-Tree можно представить в виде эквивалентного двоичного дерева. Такое дерево всегда будет иметь больше узлов, больше сравнений и менее сбалансированное (не обязательно буквально, ваш бинарный поиск это просто кусок этого бинарного дерева). То, что на практике кеш ускоряет константную составляющую и B-tree во многих случаях выходит вперед не делает его универсальным. Чем больше нивелируется влияние кеша тем быстрее двоичное дерево и наоборот. Все остальное зависит от задачи и параметров. Думаю что разработчики stl не глупее нас и лучше понимают каких задачи, на практике, встречаются чаще.kmu1990
12.09.2017 01:09Вот же.
И там прямым текстом написано что в C++ есть требования к итераторам, которые не получится эффективно реализовать для b-tree. Да уж действительно серебрянная пуля…
Опа, а как же ваш «любимый» кеш? Бинарный поиск с O(logN) разве не эквивалентен бинарному дереву?
1. Я уже писал про TLB, который вы категорически игнорируете. 2. С деревьями не только поиск, вставку и удаление производят, по ним еще иногда и итерируются.
Хотя я вроде уже упоминал, что есть разные нагрузки, и утверждать, что одна структура лучше другой независимо от нагрзуки (как вы сделали и на что я вам уже указывал) странно.
Элементов в узле то больше. Чуть выше вы же говорили про бинарный поиск.
Да говорил и?
Почитайте любую книгу по теории структур данных и вы узнаете что любое дерево, в том числе и B-Tree можно представить в виде эквивалентного двоичного дерева.
И это гарантирует функциональную эквивалентность, но не одинаковую эффективность.
Такое дерево всегда будет иметь больше узлов, больше сравнений и менее сбалансированное (не обязательно буквально, ваш бинарный поиск это просто кусок этого бинарного дерева).
Бинарное дерево полученное из b-tree может быть, но вот b-tree это всегда идеально сбалансированное дерево поиска и с учетом бинарного поиска и без него (может вам стоит самому обратиться к книгам по алгоритмам?).
То, что на практике кеш ускоряет константную составляющую и B-tree во многих случаях выходит вперед не делает его универсальным.
И я ведь нигде не говорил про универсальность, более того прямым текстом указал вам, что как минимум существует проблема с итераторами. Но вы опять же это проигнорировали или просто не поняли (к вопросу про подростковую категаричность и нежелание слушать).

Videoman
12.09.2017 11:34Ошибся комментварием. Ответ сюда
И там прямым текстом написано что в C++ есть требования к итераторам
Вы сами игнорируете аргументы. Давайте на время забудем про них.
Хотя я вроде уже упоминал, что есть разные нагрузки, и утверждать, что одна структура лучше другой независимо от нагрузки (как вы сделали и на что я вам уже указывал) странно.
А никто с этим и не споритИ это гарантирует функциональную эквивалентность, но не одинаковую эффективность.
Правильно. Пока у процессора и памяти нет операций по мгновенному сравнению всех N вершин, любое дерево отличное от бинарного потребует столько же либо больше операций сравнения и будет менее эффективным.Бинарное дерево полученное из b-tree может быть, но вот b-tree это всегда идеально сбалансированное дерево поиска и с учетом бинарного поиска и без него (может вам стоит самому обратиться к книгам по алгоритмам?).
Это в идеальном сферическом вакууме, а на практике, любое не бинарное дерево потребует количество операций такое же как в эквивалентном бинарном. Ну не умеет пока железо и память работать сразу с узлами B-tree целиком. Что бы не придумали количество операций сравнения всегда будет либо столько же, либо больше чем в эквивалентном бинарном.И я ведь нигде не говорил про универсальность, более того прямым текстом указал вам, что как минимум существует проблема с итераторами.
И я не говорил. Я, просто, не согласен с вами в том что в std::map используется бинарное дерево лишь потому, что стандарт стар. B-tree будет сильно опережать двоичное дерево там, где есть выгода по скорости от локальности данных. Особенно эта разница проявляется на внешних носителях. Также, B-tree будет иметь значительный оверхед по памяти, о чем вы тактично умалчиваете.
kmu1990
12.09.2017 21:37Вы сами игнорируете аргументы. Давайте на время забудем про них.
Вы утверждали, что я продвигаю b-tree, как серебрянную пулю и в качестве аргумента привели мое утверждение, где прямым текстом сказано обратное, а теперь предлагаете забыть про аргументы? Вы серьезно?
А никто с этим и не спорит
Вы сделали утверждение, что бинарные деревья поиска в памяти лучше b-tree безотносительно чего бы то ни было (прямо тут) вас поправили, а вы вместо того чтобы на этом успокоиться стали привелкать аргументы вроде, а там вот дяди умные сделали значит так правильно! При этом почему умные дяди приняли то или иное решение вы только гадаете. Вы только и делаете что спорите, причем спорите не аргументированно.
Правильно. Пока у процессора и памяти нет операций по мгновенному сравнению всех N вершин, любое дерево отличное от бинарного потребует столько же либо больше операций сравнения и будет менее эффективным.
И что? Из этого разве следует, что бинарное дерево как минимум не хуже b-tree по производительности? И почему вы опять лихо отбрасываете в сторону такие вещи как кеш и TLB (про которые я уже неоднократно вам упоминал)? Более того, даже большее количество сравнений само по себе не значит меньшую скорость работы.
Это в идеальном сферическом вакууме, а на практике, любое не бинарное дерево потребует количество операций такое же как в эквивалентном бинарном. Ну не умеет пока железо и память работать сразу с узлами B-tree целиком. Что бы не придумали количество операций сравнения всегда будет либо столько же, либо больше чем в эквивалентном бинарном.
Нет, b-tree идеально сбалансированное дерево поска без всяких вакуумов, тем более сферических. И опять же напомню, хотя зря наверно, что речь ведь не только о количестве сравнений, но о производительности на реальном железе (да-да том самом железе, где есть кеш и TLB, если повезет).
Я, просто, не согласен с вами в том что в std::map используется бинарное дерево лишь потому, что стандарт стар.
Вы не согласны со мной? А где я такое утверждал, чтобы вы со мной были не согласны? Более того я вам говорил уже несколько раз про проблему с итераторами (и при этом ни разу ни слова не сказал про чей бы то ни было возраст).
Также, B-tree будет иметь значительный оверхед по памяти, о чем вы тактично умалчиваете.
Ну да? А вы это видели? Опять же b-tree будет иметь оверхед по памяти (о котором я оказывается тактично умалчиваю) безотносительно чего бы то ни было?
Вообще у меня складываеится впечатление, что вы посмотрели, что в std::map используется бинарное дерево поиска, а потом уже на основании того, что std::map же умные дяди сделали, стали подтягивать всякую разную (и не всегда корректную) аргументацию, чтобы оправдать это решение.


alexander_8901
Было бы интересно увидеть сравнение скорости работы (вставка/поиск/и т.д.) с другими реализациями.