Пускай у нас есть некий ряд ячеек, часть которых можно пометить как «занятые»:


Нам нужно узнать, сколько всего существует вариантов расположения занятых ячеек.

К этой схеме сводится множество задач. Например, разбиение периода из N + 1 календарных дней на l + 1 следующих друг за другом меньших периодов. Допустим, мы хотим провести оптимизационный расчет методом «грубой силы», рассчитав целевую функцию для каждого возможного варианта разбиения периода, чтобы выбрать наилучший вариант. Чтобы заранее оценить время расчета, нужно определить количество вариантов. Это поможет принять решение, стоит ли вообще начинать расчет. Согласитесь — полезно будет заранее предупредить пользователя вашей программы, что с теми параметрами, которые он задал, расчет займет 10000 лет.

Существует простая формула, позволяющая для любых N и l получить количество всех возможных вариантов расположения занятых ячеек:

$$

$$

, где n = N – l + 1, n ? 0.

Это формула суммы сумм сумм … сумм арифметических прогрессий вида 1 + 2 + 3 + … + n; слово «сумма» в разных склонениях в этой фразе повторяется ровно l – 1 раз. Другими словами, эта формула позволяет быстро вычислять вот такие суммы:

$$

$$

У обычного настольного ПК уходит слишком много времени на вычисление этих сумм «в лоб» (особенно с использованием длинной арифметики — а без нее не обойтись).

Когда я только начинал решать эту задачу (и еще не знал этой формулы), я забивал в поисковик фразу «сумма сумм арифметических прогрессий» и ничего не находил. Именно так я и назвал свою статью — в расчете, что следующий искатель этой формулы сможет быстро найти ее здесь.

Ссылки на авторитетный источник касательно этой формулы у меня нет. Я ее вывел аналитически и проверил численно, проведя свыше 4000 тестов. Ее вывод, если кому интересно, приведен в конце статьи.

Скоро я расскажу, какое отношение имеют арифметические прогрессии к подсчету вариантов расположения ячеек, а пока приведу еще несколько готовых формул.

Введем дополнительное условие: допустим, в любом раскладе должна быть хотя бы 1 группа из r смежных незанятых ячеек. В этом случае, количество вариантов определяется так:

$$

$$

$$

$$

$$

$$

Вывод этой формулы следует в самом конце статьи.

Если ваша программа проводит какие-либо расчеты для каждого варианта расположения ячеек, то расчеты для разных вариантов наверняка однотипные. Это значит, что их легко распределить по нескольким потокам. В статье будет рассказано, как организовать итерацию по вариантам, чтобы каждому потоку досталось равное количество вариантов.

1. Причем тут прогрессии?

Это самый легкий вопрос. Сгруппируйте все занятые ячейки в левом конце вашего ряда ячеек — чтобы они следовали одна за другой, начиная с крайней левой ячейки в ряду:


Сколько существует вариантов расположения самой правой из занятых ячеек (будем называть ее последней занятой ячейкой), при условии, что остальные ячейки остаются на своих местах? Ровно n. Теперь сдвиньте ПРЕДпоследнюю занятую ячейку вправо на 1 позицию. Сколько останется позиций для последней ячейки? n – 1. Предпоследнюю ячейку можно сдвинуть вправо n раз. Значит, вариантов расположения двух последних занятых ячеек будет вот столько: S₂(n) = 1 + 2 + 3 + … + n. Сдвиньте третью справа занятую ячейку на 1 позицию и снова подсчитайте количество вариантов расположения последней и предпоследней ячеек. Получится S₂(n – 1). Третью ячейку тоже можно сдвинуть вправо только n раз, и всего вариантов расположения трех последних ячеек будет S₃(n) = S₂(1) + S₂(2) + … + S₂(n).

Рассуждая так, доберемся наконец и до количества вариантов расположения всех l занятых ячеек:

$$

$$

2. Дополнительное условие: хотя бы 1 группа из r незанятых смежных ячеек

Сначала рассмотрим частные случаи. Если n + l – 1 ? r(l + 1), то ни при каком раскладе мы не получим варианта, в котором нет хотя бы 1 группы из r незанятых ячеек. Даже в самом худшем случае — когда занятые ячейки в ряду расположены равномерно, так чтобы расстояние между ними и краями ряда было равно r – 1, количества занятых ячеек просто не хватит на то, чтобы ВСЕ эти расстояния были не больше r – 1. Хотя бы одно будет равно как минимум r. Следовательно:

$$

r = 0 означает, что нас устраивает любое расположение ячеек. Условие «n + l – 1 ? r(l + 1)» в этом случае выполняется при любых n и l:

$$

Если же r = 1, то условие «n + l – 1 ? r(l + 1)» выполняется только при n > 1:

$$

n ? r означает, что число незанятых ячеек меньше r, и нет никакой возможности получить r незанятых ячеек, смежных или нет. Поэтому в предыдущей формуле и стоит 0 при n = 1.

$$

Если занятых ячеек нет, то вариант их расположения всего один:

$$

Теперь — обобщенная формула для всех остальных случаев.

Если зафиксировать самую левую занятую ячейку в крайнем левом положении, вариантов расположения всех остальных ячеек будет S^r_{(l – 1)} (n). Если сдвинуть ее на 1 позицию вправо, вариантов будет S^r_{(l – 1)} (n – 1). Начиная с позиции r + 1, у нас всегда будет промежуток длиной не менее r в левом конце ряда, так что остальные варианты можно будет посчитать без рекурсии: S_l (n – r). Получается вот что:

$$

Формула верная, но я предпочитаю пользоваться вот этой:

$$

По моим замерам, она в десятки раз быстрее предыдущей. Выводить ее несложно, но описывать вывод долго. В конце статьи расскажу.

Теперь мы можем перейти к распределению итераций по потокам. Чтобы разобраться в этом, вы должны ясно понимать, как выводилась первая формула S^r_l (n), т.к. в этом выводе заложен определенный порядок итерации по вариантам расположения занятых ячеек.

3. Как организовать итерацию в нескольких потоках

Порядок итерации будет общим для всех потоков. Вначале все l ячеек располагаются в левом конце ряда, занимая позиции с 1 по l. Это первая итерация. Крайняя правая ячейка на каждой итерации сдвигается вправо на 1 позицию, пока не окажется в конце ряда, затем ячейка слева от нее сдвигается на 1 позицию вправо, и крайняя ячейка снова проходит все возможные положения между ячейкой слева и правым концом ряда. Когда обе ячейки оказываются в крайнем правом положении, ячейка слева от них сдвигается на 1 позицию вправо. И так пока все ячейки не окажутся в правом конце ряда. При итерации мы пропускаем варианты, в которых нет ни одной группы из r смежных незанятых ячеек.

Выберем согласно этому порядку итерации первые k вариантов и назначим их первому потоку, затем следующие k вариантов назначим второму потоку, и так далее. Допустим, мы решили задействовать n_t потоков, количество итераций в каждом из которых мы определили как k_i, i = 1, …, n_t.

Порядковый номер первой итерации для каждого потока назовем h_i:

$$

Имея начальное расположение ячеек для варианта под номером h_i, не составит труда провести k_i итераций, начиная с этого варианта (я даже описывать не буду, как это делается). Однако нам понадобится функция, вычисляющая положение занятых ячеек по порядковому номеру варианта:

using Anylong = boost::multiprecision::cpp_int;
using Opt_UVec = boost::optional<std::vector<unsigned> >;
Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0);

Функция arrangement принимает номер варианта index и параметры ряда: n = N – l + 1, l и r, — а возвращает вектор с позициями занятых ячеек в ряду. Позиция занятой ячейки — это целое число от 1 до N.

Число вариантов очень быстро растет с увеличением параметров l и n, поэтому для представления этого числа нам требуется длинная арифметика. Я использовал класс boost::multiprecision::cpp_int, способный представлять целые числа любой длины.

Если параметр index превышает число возможных вариантов расположения ячеек, функция возвращает пустой объект boost::optional. Если параметр index или параметр n равен 0, это рассматривается как ошибка программиста, и функция генерирует исключение.

Сначала переведем на C++ формулы для определения числа вариантов:

struct Exception
{
    enum class Code { INVALID_INPUT = 1 } code;

    Exception(Code c) : code(c) {}
    static Exception InvalidInput() { return Exception(Code::INVALID_INPUT); }
};

Anylong S(unsigned n, unsigned l)
{
    if (!n) throw Exception::InvalidInput();
    if (l == 1) return n;
    if (n == 1 || l == 0) return 1;
    Anylong res = 1;
    for (unsigned i = 1; i <= l; ++i) {
        res = res * (n + i - 1) / i; // порядок действий важен!
    }
    return res;
}

Anylong S(unsigned n, unsigned l, unsigned r)
{
    if (!n) throw Exception::InvalidInput();
    if (r == 0) return S(n, l);
    if (r == 1) if (n == 1) return 0; else return S(n, l);
    if (n + l - 1 >= r * (l + 1)) return S(n, l);
    if (n <= r) return 0; else if (l == 0) return 1;

    Anylong res = (l + 1) * S(n - r, l);
    for (unsigned j = 0; j <= l - 1; ++j)
        for (unsigned i = r; i <= n - r - 1; ++i)
            res -= S(i + 1, j, r) * S(n - r - i, l - j - 1);
    return res;
}

Обратите внимание на эту строчку:

        res = res * (n + i - 1) / i;

Здесь важен порядок действий. Произведение множителей res и (n + i – 1) всегда делится нацело на i, а каждый из них в отдельности — нет. Нарушение порядка действий приведет к искажению результатов.

Теперь стоит вопрос, как определить вариант расположения по индексу.

Вспомним принятый нами порядок итерации. Чтобы сдвинуть крайнюю левую ячейку на 1 позицию вправо, потребуется X₁=S^r_{l – 1} (n) итераций. Сдвинуть ее еще на 1 ячейку правее можно за X₂=S^r_{l – 1} (n – 1) итераций. Если в какой-то момент X₁ + X₂ + … + X_i + X_{i + 1} оказалось больше, чем index, значит, мы только что определили положение первой занятой ячейки. Она должна находиться на i-й позиции. Далее вычисляем, сколько итераций требуется, чтобы сдвинуть вправо вторую ячейку: X₁=S^r_{l – 2} (n – i + 1). Так продолжается, пока мы не доберемся до варианта под номером index. Если хоть раз i оказалось больше r, все последующие вызовы S^r_l (n) заменяются на S_l (n), ведь у нас уже есть как минимум один промежуток длиной не меньше r слева от текущей ячейки.

Короче будет написать код, чем объяснять словами.

Opt_UVec arrangement(Anylong index, unsigned n, unsigned l, unsigned r = 0)
{
    if (index == 0) throw Exception::InvalidInput();
    if (index > S(n, l, r)) return {};
    std::vector<unsigned> oci(l); /* occupied cells indices - позиции
                              занятых ячеек в ряду (индексы от 1 до N) */
    if (l == 0) return oci;
    if (l == 1) {
        assert(index <= std::numeric_limits<unsigned>::max());
        oci[0] = (unsigned)index;
        return oci;
    }
    oci[0] = 1;

    unsigned N = n + l - 1;
    unsigned prev = 1;
    
    Anylong i = 0; auto it = oci.begin();
    while (true) {
        auto s = S(n, --l, r);
        while (i + s <= index) {
            if ((i += s) == index) {
                auto it1 = --oci.end();
                if (it1 == it) return oci;
                *it1 = N;
                for (it1--; it1 != it; it1--) *it1 = *(it1 + 1) - 1;
                return oci;
            }
            s = S(--n, l, r);
            assert(n);
            (*it)++;
            if (r && (*it) > prev + r - 1) r = 0;
        }
        prev = *it++;
        assert(it != oci.end());
        *it = prev + 1;
    }
    assert(false);
}

4. Вывод формул

Порадую любителей школьной алгебры еще одним разделом.

Начнем с суммы сумм арифметических прогрессий:

$$

$$

Как видим, при l = 0 S₀ (n) = 1 — это многочлен 0-й степени. При l = 1 S₁ (n) = n — это многочлен 1-й степени. При l = 2 используется известная формула суммы арифметической прогрессии S₂ (n) = n(n + 1)/2. И это многочлен 2-й степени. Можно предположить, что при l = 3 у нас будет многочлен 3-й степени. Вычислим вручную значения S₃ (n) при n = 1, 2, 3 и 4, составим систему линейных уравнений и найдем коэффициенты этого многочлена. Результат разложим на множители и получим вот это:

$$

У нас тут очевидная закономерность. Запишем вот такую формулу:

$$

Она еще не доказана для l = 3, но уже доказана для l = 1 и l = 2. Воспользуемся методом математической индукции. Предположим, что формула S_{l – 1} (n) верна для любых n и докажем, что в этом случае верна и формула S_l (n).

$$

$$

Вычтем второе из первого:

$$

$$

$$

Получилось верное тождество.

Теперь вернемся к формуле подсчета вариантов при r ? 0:

$$

Выводится она следующим образом.

Подсчитаем количество вариантов, когда промежуток между последней занятой ячейкой и правым концом ряда больше или равен r. Это как если бы последняя занятая ячейка выросла в размерах до r + 1, а размеры ряда при этом остались бы прежними:



Такое количество вариантов равно S_l(n – r).

Теперь прибавим к нему количество вариантов, в которых промежуток между последней и предпоследней занятыми ячейками больше или равен r. Это количество вариантов снова будет равно S_l(n – r). Но некоторые из этих вариантов мы уже посчитали, когда вычисляли предыдущие S_l(n – r). А именно — те варианты, в которых промежуток между последней занятой ячейкой и правым концом ряда больше или равен r. Значит, к первым S_l(n – r) вариантов нужно прибавить не S_l(n – r), а S_l(n – r) – X, где X — количество вариантов, в которых промежуток между последней и предпоследней занятыми ячейками больше или равен r, равно как и промежуток между последней занятой ячейкой и правым концом ряда.

Ровно то же самое придется сделать для каждой j-й занятой ячейки — из S_l(n – r) вычесть X_j, равное количеству вариантов, в которых промежуток между j-й ячейкой и ячейкой слева от нее (в случае крайней левой ячейки — промежуток между нею и левым концом ряда), а также хотя бы один из промежутков справа от j-й ячейки — больше или равны r.

Всего у нас l – 1 промежутков между занятыми ячейками, плюс 2 промежутка между занятой ячейкой и концом ряда. Значит, слагаемое S_l(n – r) входит в нашу формулу l + 1 раз. А вот X_j не вычисляется для промежутка между крайней правой занятой ячейкой и правым коном ряда. Значит, этих слагаемых будет только l.

$$

j находится в диапазоне от 0 до l – 1. Такой уж я принял порядок индексации. Тогда количество занятых ячеек справа от j-й ячейки равно j.

Посмотрите на этот рисунок:


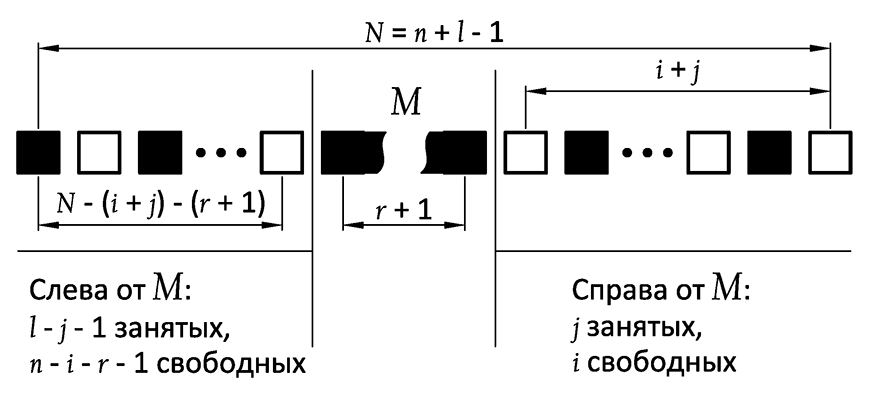
j-я ячейка (та, что увеличивается до размера r + 1 при итерации по j) обозначается как M. Она может находиться в n – r возможных положениях, которые определяются параметром i (i ? [0, n – r – 1]). Первые r положений можно не рассматривать, поскольку при i < r все промежутки справа от M будут меньше r. Следовательно, i ? [r, n – r – 1].

Количество вариантов расположения ячеек справа от M, в которых хотя бы 1 промежуток больше или равен r, равно S^r_j (i + 1). Количество вариантов расположения ячеек слева от M равно S_{l – j – 1} (n – i – r). Всего вариантов получается S^r_j (i + 1)•S_{l – j – 1} (n – i – r) для всех i ? [r, n – r – 1] и всех j ? [0, l – 1]:

$$

Это и есть наша формула.