Всем привет! Недавно нужно было написать код для реализации сегментации изображения с помощью метода k – средних (англ. k-means). Ну, первым делом Google в помощь. Нашел много информации, как и с математической точки зрения (всякие там сложные математические каракули, хрен поймёшь, что там написано), так и некоторые программные реализации, которые есть в английском интернете. Эти коды конечно прекрасны – спору нет, но саму суть идеи сложно поймать. Как – то оно там все сложно, запутано, да и пока сам, ручками, не пропишешь код, ничего не поймешь. В этой статье хочу показать простую, не производительную, но, надеюсь, понятную реализацию этого чудесного алгоритма. Ладно, погнали!

Итак, что такое кластеризация с точки зрения нашего восприятия? Приведу пример, допустим, есть милое изображение с цветочками с дачи твоей бабушки.



Вопрос следующий: определить, сколько на данном фото участков, залитых приблизительно одним цветом. Ну это совсем не сложно: белые лепестки – раз, желтые центры – два (я не биолог, как они именуются, не знаю), зелень – три. Эти участки и называются кластерами. Кластер -объединение данных, имеющих общие признаки (цвет, положение и т.д.). Процесс определения и помещения каждой составляющей каких-либо данных в такие кластеры — участки и называется кластеризацией.

Есть много алгоритмов кластеризации, но самый простой из них — k – средних, о котором дальше и пойдет речь. K-средних – простой и эффективный алгоритм, который легко реализовать программным методом. Данные, которые мы будем распределять по кластерам — пиксели. Как известно, цветной пиксель имеет три составляющих — red, green и blue. Наложение этих составляющих и создает палитру существующих цветов.



В памяти компьютера каждая составляющая цвета характеризуется числом от 0 до 255. То есть комбинируя различные значения красного, зеленого и синего, получаем палитру цветов на экране.

На примере пикселей мы и реализуем наш алгоритм. K-средних – итерационный алгоритм, то есть он даст правильный результат, после энного количества повторов некоторых математических вычислений.

Алгоритм

1. Нужно наперед знать в сколько кластеров нужно распределить данные. Это является существенным минусом данного метода, но эта проблема решается улучшенными реализациями алгоритма, но это, как говорят, совсем другая история.
2. Нужно выбрать начальные центры наших кластеров. Как? Да наугад. Зачем? Чтобы можно было привязывать каждый пиксель к центру кластера. Центр – это как Король, вокруг которого собираются его подданные — пиксели. Именно «расстояние» от центра до пикселя определяет, кому будет подчиняться каждый пиксель.
3. Посчитаем расстояние от каждого центра до каждого пикселя. Это расстояние считается как евклидово расстояние между точками в пространстве, а в нашем случае — как расстояние между тремя составляющими цвета:

   $\$\$display\$\$\backslash sqrt\{(R\_\{2\}-R\_\{1\})^2\; +(G\_\{2\}-G\_\{1\})^2\; +(B\_\{2\}-B\_\{1\})^2\}.\$\$display\$\$$

   Считаем расстояние от первого пикселя до каждого центра и определяем наименьшее расстояние между этим пикселем и центрами. Для центра расстояние, до которого является наименьшим, пересчитываем координаты, как среднее арифметическое между каждой составляющей пикселя – короля и пикселя — подданного. Наш центр смещается в пространстве соответственно подсчетам.
4. После пересчета всех центров, мы распределяем пиксели по кластерам, сравнивая расстояние от каждого пикселя до центров. Пиксель помещается в кластер, к центру которого он расположен ближе, чем к остальным центрам.
5. Все начинается сначала, до тех пор, пока пиксели остаются в одних и тех же кластерах. Часто такого может и не случится, так как при большом количестве данных центры будут перемещаться в малом радиусе, и пиксели по краям кластеров будут прыгать то в один, то в другой кластер. Для этого нужно определить максимальное число итераций.

Реализация

Реализовывать данный проект я буду на С++. Первый файл – «k_means.h», в нем я определил основные типы данных, константы, и основной класс для работы — «K_means».
Для характеристики каждого пикселя создадим структуру, которая состоит из трех составляющих пикселя, для которых я выбрал тип double для более точных расчетов, а также определил некоторые константы для работы программы:

const int KK = 10;  //количество кластеров
const int max_iterations = 100;  //максимальное количество итераций

typedef struct {           
	double r;
	double g;
	double b;
} rgb;

Сам класс K_means:

class K_means
{
private:
	std::vector<rgb> pixcel; 
	int q_klaster;           
	int k_pixcel;            
	std::vector<rgb> centr;  
	void identify_centers(); 
	inline double compute(rgb k1, rgb k2)
	{
		return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2));
	}
	inline double compute_s(double a, double b) {
		return (a + b) / 2;
	};
public:
	K_means() : q_klaster(0), k_pixcel(0) {}; 
	K_means(int n, rgb *mas, int n_klaster);
	K_means(int n_klaster, std::istream & os);
	void clustering(std::ostream & os); 
	void print()const;
	~K_means();
	friend std::ostream & operator<<(std::ostream & os, const K_means & k);
};

Пробежимся по составляющим класса:

vectorpixcel — вектор для пикселей;
q_klaster – количество кластеров;
k_pixcel – количество пикселей;
vectorcentr – вектор для центров кластеризации, количество элементов в нем определяется q_klaster;
identify_centers() – метод для случайного выбора начальных центров среди входных пикселей;
compute() и compute_s() встроенные методы для расчета расстояния между пикселями и пересчета центров соответственно;
три конструктора: первый по умолчанию, второй — для инициализации пикселей из массива, третий — для инициализации пикселей из текстового файла (в моей реализации сначала файл случайно заполняется данными, и потом с этого файла считываются пиксели для работы программы, почему не напрямую в вектор – просто так нужно в моем случае);
clustering(std::ostream & os) – метод кластеризации;
метод и перегрузка оператора вывода для публикации результатов.

Реализация методов:

void K_means::identify_centers()
{
	srand((unsigned)time(NULL));
	rgb temp;
	rgb *mas = new rgb[q_klaster];
	for (int i = 0; i < q_klaster; i++) {
		temp = pixcel[0 + rand() % k_pixcel];
		for (int j = i; j < q_klaster; j++) {
			if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) {
				mas[j] = temp;
			}
			else {
				i--;
				break;
			}
		}
	}
	for (int i = 0; i < q_klaster; i++) {
		centr.push_back(mas[i]);
	}
	delete []mas;
}

Это метод для выбора начальных центров кластеризации и добавления их в вектор центров. Осуществляется проверка на повтор центров и замена их в этих случаях.

K_means::K_means(int n, rgb * mas, int n_klaster)
{
	for (int i = 0; i < n; i++) {
		pixcel.push_back(*(mas + i));
	}
	q_klaster = n_klaster;
	k_pixcel = n;
	identify_centers();
}

Реализация конструктора для инициализации пикселей из массива.

K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster)
{
	rgb temp;
	while (os >> temp.r && os >> temp.g && os >> temp.b) {
		pixcel.push_back(temp);
	}
	k_pixcel = pixcel.size();
	identify_centers();
}

В этот конструктор мы передаем объект ввода для возможности ввода данных как из файла, так и из консоли.

void K_means::clustering(std::ostream & os)
{
	os << "\n\nНачало кластеризации:" << std::endl;
/*В эти векторы мы будем помещать информацию о принадлежности каждого пикселя к определенному кластеру: в одном векторе будет информация о предыдущей итерации, а в другом - о текущей, и если они равны, то цикл заканчивается, так как каждый пиксель остался на своем месте.*/
	std::vector<int> check_1(k_pixcel, -1);
	std::vector<int> check_2(k_pixcel, -2);
	int iter = 0;
/*Количество итераций.*/
	while(true)
	{
		os << "\n\n---------------- Итерация №" 
			<< iter << " ----------------\n\n";
		{
			for (int j = 0; j < k_pixcel; j++) {
				double *mas = new double[q_klaster];
/*Первая часть алгоритма: берем пиксель и находим расстояние от него до каждого центра. Данные помещаем в динамический массив размерностью, равной количеству кластеров.*/
				for (int i = 0; i < q_klaster; i++) {
					*(mas + i) = compute(pixcel[j], centr[i]);
					os << "Расстояние от пикселя " << j << " к центру #" 
						<< i << ": " << *(mas + i) << std::endl;
				}
/*Определяем минимальное расстояние и в m_k фиксируем номер центра для дальнейшего пересчета.*/
				double min_dist = *mas;
				int m_k = 0;
				for (int i = 0; i < q_klaster; i++) {
					if (min_dist > *(mas + i)) {
						min_dist = *(mas + i);
						m_k = i;
					}
				}

				os << "Минимальное расстояние к центру #"  << m_k << std::endl;
				os << "Пересчитываем центр #" << m_k << ": ";
				centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r);
				centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g);
				centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b);
				os << centr[m_k].r << " " << centr[m_k].g 
					<< " " << centr[m_k].b << std::endl;
				delete[] mas;
			}
/*Классифицируем пиксели по кластерам.*/
			int *mass = new int[k_pixcel];
			os << "\nПроведем классификацию пикселей: "<< std::endl;
			for (int k = 0; k < k_pixcel; k++) {
				double *mas = new double[q_klaster];
/*Находим расстояние до каждого центра.*/
				for (int i = 0; i < q_klaster; i++) {
					*(mas + i) = compute(pixcel[k], centr[i]);
					os << "Расстояние от пикселя №" << k << " к центру #" 
						<< i << ": " << *(mas + i) << std::endl;
				}
/*Определяем минимальное расстояние.*/
				double min_dist = *mas;
				int m_k = 0;
				for (int i = 0; i < q_klaster; i++) {
					if (min_dist > *(mas + i)) {
						min_dist = *(mas + i);
						m_k = i;
					}
				}
				mass[k] = m_k;
				os << "Пиксель №" << k << " ближе всего к центру #" << m_k << std::endl;
			}
/*Выводим информацию о принадлежности пикселей к кластерам и заполняем вектор для сравнения итераций.*/
			os << "\nМассив соответствия пикселей и центров: \n";
			for (int i = 0; i < k_pixcel; i++) {
				os << mass[i] << " ";
				check_1[i] = *(mass + i);
			}
			os << std::endl << std::endl;

			os << "Результат кластеризации: " << std::endl;
			int itr = KK + 1;
			for (int i = 0; i < q_klaster; i++) {
				os << "Кластер #" << i << std::endl;
				for (int j = 0; j < k_pixcel; j++) {
					if (mass[j] == i) {
						os << pixcel[j].r << " " << pixcel[j].g
							<< " " << pixcel[j].b << std::endl;
						mass[j] = ++itr;
					}
				}
			}

			delete[] mass;
/*Выводим информацию о новых центрах.*/
			os << "Новые центры: \n" ;
			for (int i = 0; i < q_klaster; i++) {
				os << centr[i].r << " " << centr[i].g
					<< " " << centr[i].b << " - #" << i << std::endl;
			}
		}
/*Если наши векторы равны или количество итераций больше допустимого – прекращаем процесс.*/
		iter++;
		if (check_1 == check_2 || iter >= max_iterations) {
			break;
		}
		check_2 = check_1;
	}
	os << "\n\nКонец кластеризации." << std::endl;
}

Основной метод кластеризации.

std::ostream & operator<<(std::ostream & os, const K_means & k)
{
	os << "Начальные пиксели: " << std::endl;
	for (int i = 0; i < k.k_pixcel; i++) {
		os << k.pixcel[i].r << " " << k.pixcel[i].g
			<< " " << k.pixcel[i].b << " - №" << i << std::endl;
	}
	os << std::endl << "Случайные начальные центры кластеризации: " << std::endl;
	for (int i = 0; i < k.q_klaster; i++) {
		os << k.centr[i].r << " " << k.centr[i].g << " "
			<< k.centr[i].b << " - #" << i << std::endl;
	}
	os << "\nКоличество кластеров: " << k.q_klaster << std::endl;
	os << "Количество пикселей: " << k.k_pixcel << std::endl;
	return os;
}

Вывод начальных данных.

Пример вывода

Этот пример спланирован наперед, пиксели выбраны специально для демонстрации. Программе достаточно двух итераций, чтобы сгруппировать данные в три кластера. Посмотрев на центры двух последних итераций, можно заметить, что они практически остались на месте.

Интереснее случаи при рандомной генерации пикселей. Сгенерировав 50 точек, которые нужно поделить на 10 кластеров, я получил 5 итераций. Сгенерировав 50 точек, которые нужно поделить на 3 кластера, я получил все 100 максимально допустимых итераций. Можно заметить, что чем больше кластеров, тем легче программе найти наиболее схожие пиксели и объединить их в меньшие группы, и наоборот — если кластеров мало, а точек много, часто алгоритм завершается только от превышения максимально допустимого количества итераций, так как некоторые пиксели постоянно прыгают из одного кластера в другой. Тем не менее, основная масса все равно определяются в свои кластеры окончательно.

Ну а теперь давайте проверим результат кластеризации. Взяв результат некоторых кластеров из примера 50 точек на 10 кластеров, я вбил результат этих данных в Illustrator и вот что получилось:



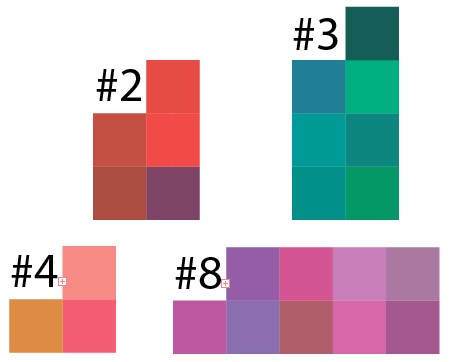
Видно, что в каждом кластере преобладают какие-либо оттенки цвета, и тут нужно понимать, что пиксели были выбраны случайно, аналогом такого изображения в реальной жизни является какая-то картина, на которую случайно набрызгали всех красок и выделить участки схожих цветов сложно.

Допустим, у нас есть такое фото. Остров мы можем определить, как один кластер, но при увеличении мы видим, что он состоит из разных оттенков зеленого.



А это 8 кластер, но в уменьшенном варианте, результат аналогичен:



Полную версию программы можно посмотреть на моем GitHub.