Вместо предисловия
Допустим, сидя вечерком в теплом кресле вам вдруг пришла в голову шальная мысль: «Хм, а почему бы мне вместо случайного подбора гиперпараметров модели не узнать, а почему оно всё работает?»
Это скользкий путь — вы думаете, что достаточно пары вечеров с неторопливым чтением главки «Глубокого обучения» или 5-минутных youtube-роликов с различных MOOC; на деле, чтобы создать понимание, а не его иллюзию, требуется приличное количество времени (ну уж никак не меньше полугода для самых фанатичных); но самое печальное — профит от этого мероприятия не очевиден — к счастью (или к сожалению), мир не устроен по законам математики, и будь вы трижды доктором физмат наук — некоторые модели всё равно будут работать лучше только в том случае, если вы подкинете в них побольше предобработанных данных либо соорудите огромный ансамбль.
Я считаю своим долгом вас предупредить, что это кривая дорожка, и возможно, что вложения в математику окупятся не так скоро, как того бы хотелось. Но математика интересна сама по себе, безотносительно приложений. Тем более что если вас заинтересовало, а что же происходит в этом черном ящике с гиперпараметрами, то это означает, что математика вам, скорее всего, не безразлична.
Ещё кое-что про мои рекомендации: я не люблю математическую литературу, которая кишит индексами, перлами типа «a_ijk с тремя подчеркиваниями и шляпкой сопряженное». Я считаю, что идеи важнее строгих выводов. При этом идеи не должны скатываться до «рукомаханий», всё должно быть довольно строго. Я не люблю книги наподобие Бурбаки и Кнута. На мой взгляд, эти книги предназначены для чего угодно, но не для чтения и не для изучения предмета. Они хороши в качестве ссылок и как энциклопедии.
Напоследок приведу кое-что из Бертрана Рассела:
Евклид презирал практическую полезность, которую внедрял Платон. Говорят, что один ученик, прослушав доказательства, спросил, что выиграет он изучением геометрии; тогда Евклид позвал раба и сказал: «Дай молодому человеку грош, поскольку он непременно должен извлекать выгоду из того, что изучает».Теперь перейду собственно к основной части.
Пререквизиты
- Я предполагаю, что вы более-менее ориентируетесь в школьном курсе математики.
- Я предполагаю, что вы с английским не совсем на «вы», поскольку много дельной литературы и курсов написаны и рассказаны именно на этом языке. Математический английский не такой страшный, как английский вообще; это довольно ограниченный лексикон со стандартно построенными предложениями, без мешанины времён, без буйства красок и т.д.
- Я предполагаю, что у вас есть верёвка, которой вы можете привязать себя к стулу.
Уровни сложности
Не секрет, что по каждой математической дисциплине написано много литературы, и иногда проблемой становится даже простой выбор нужной книги. Я буду выделять несколько уровней сложности в литературе, что вы знали, куда стоит соваться, а куда лезть (пока что) не надо (или к чему можно обратиться для более полной информации).
- Bring it on — основная рабочая лошадка; это книги, что называется, «must have».
- Hurt me plenty — уровень повыше, позволяет оглядеть с высоты птичьего полёта уровень 1, систематизирует знания, объединяет различные области знаний.
- Nightmare — для сильных духом, уровень мехмата, для любителей математики и башен из слоновой кости.
Дорожная карта
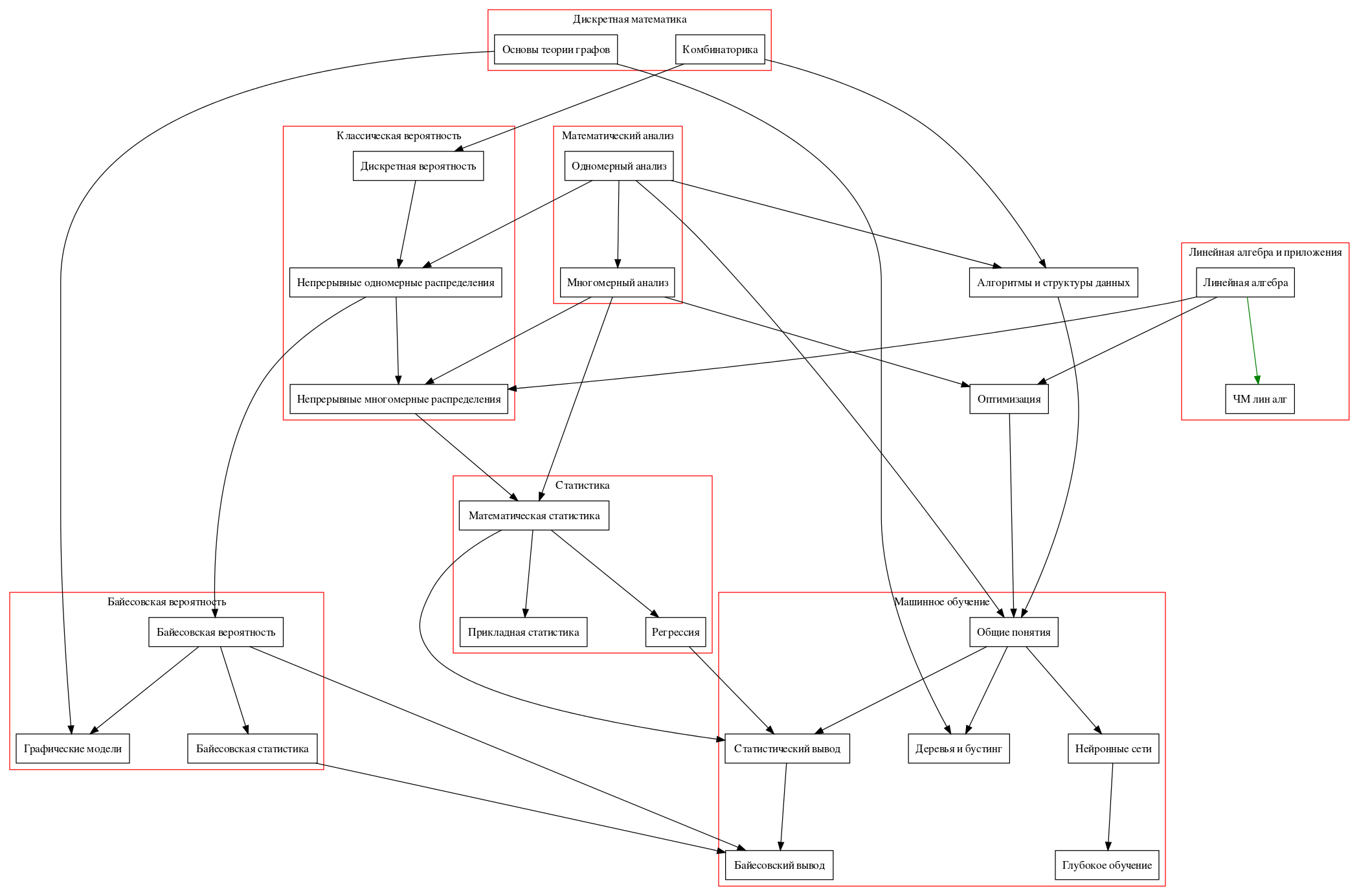
Перейду собственно к конкретным курсам.
Анализ, он же calculus
В российских вузах его преподают довольно интересно: большинство через несколько лет после окончания курса помнят смутно лишь какие-то там интегралы, и кажется что-то ещё. И это при том, что анализ — дисциплина прямо-таки одна из основополагающих в математике вообще. Мостиков от теории к практике как правило нет, и этот курс, подобно летающему острову парит где-то в головах, абсолютно оторванный от реальной жизни. Преодолевать это надо решением задач, причем не только из области математики, но и желательно что-либо из «реальной жизни».
Что нужно знать из анализа?
Основные вещи, которые нам понадобятся — понятие предела, непрерывности, производной, функции многих переменных, градиента, интеграла, интеграла с переменным верхним пределом, многомерного интеграла*.
Литература
Bring it on: тут всё более-менее стандартно — Пискунов / Фихтенгольц.
Hurt me plenty: Зорич, том 1. Эту книгу я люблю очень-очень сильно; это не учебник, но роман в формулах, что-то наподобие Евгения Онегина. К сожалению, он сложнее стандартных курсов по анализу за счет того, что многие вещи в нём даются более общО, и к этому надо привыкнуть; зато за счёт этой общности связываются воедино многие разрозненные вещи (см. те же пределы по базе).
Nightmare: Зорич том1 + том2, Рудин «Основы математического анализа», Львовский «Лекции по математическому анализу», Ramanan «Global Calculus».
В общем и целом резюме тут такое: литературы по анализу даже на русском языке полно; учебники чаще тяготеют к чисто математическим. В качестве дополнения к учебникам уровня 2-3 могу посоветовать несколько курсов:
Курсы из лектория МФТИ по анализу я не смотрел, но для полноты картины тоже приведу:
Практика
Практиковаться и применять полученные знания не то что «опционально», но строго-настрого ОБЯЗАТЕЛЬНО, иначе вся теория повиснет на вас мёртвым грузом, и вы быстро пойдете ко дну, причем даже не осознавая этого.
Предлагаю рассмотреть следующие варианты: Демидович, problem sets с курсов MIT (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Линейная алгебра
Хлеб насущный для Data Science и вообще для науки в целом. К сожалению, люди научились хорошо решать только линейные уравнения и их системы; для уравнений степени 2 и выше существуют всяческие очень нетривиальные теории (коммутативная алгебра, алгебраическая геометрия и иже с ними). Поэтому в анализе данных в основном применяются линейные модели (либо обобщенные линейные модели, как логистические регрессии, перцептроны и т.д.).
На русском языке много книг по линейной алгебре. Проблема в том, что они написаны либо для математиков, либо в них удручающе много индексов (и за деревьями не видно леса). Часто акцент в университетских курсах делается на жордановой форме; про другие стандартные формы часто не упоминается; есть Гаусс и бестолковый Крамер, но редко что бывает про LU, про SVD.
Что нужно знать из линейной алгебры?
Понятие вектора и векторного пространства; понятие линейного оператора; связь операторов и матриц; матричные разложения (LU, SVD как минимум); собственные вектора и собственные значения; ортогональные, унитарные операторы; симметричные и эрмитовы операторы; квадратичные формы, приведение к главным осям.
Литература
Bring it on: курс OCW-MIT Гилберта Стрэнга по линейной алгебре + его книжка.
ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/index.htm
Самое хорошее в этом курсе — отсутствие «сложных» и довольно бестолковых теорем линейной алгебры, всяческих двойственных пространств, большое количество задач в книге, практико-ориентированный подход (не «что это такое», а «как это посчитать»). Более толковых курсов по линейной алгебре я ещё не встречал.
Hurt me plenty: Axler «Linear algebra done right»; Гельфанд «Лекции по линейной алгебре»; курс МФТИ lectoriy.mipt.ru/course/LinearAlgebra; Кострикин «Введение в алгебру, часть 2», Тыртышников «Матричный анализ и линейная алгебра».
Проблема книг и курсов с этого уровня сложности в том, что они теоретико-ориентированные. Есть линейные функционалы и двойственные пространства, но нет матрицы проекции на подпространство и практических способов вычисления собственных значений. Скорее всего, курсы с этого уровня придётся дополнять сильной практикой; к примеру, численными методами линейной алгебры.
Про последнюю книгу отдельно. На мой взгляд, это одна из самых удачных русскоязычных книг по линейной алгебре в том смысле, что она не очень сильно оторвана от практики; при этом в ней содержатся и всяческие «продвинутые» темы. Она в какой-то мере может заменить лекции Стрэнга полностью, но её надо дополнять простыми задачами на «набить руку». Задачки в этой книге есть, но они довольно суровые.
Nightmare: Кострикин-Манин «Линейная алгебра и геометрия», Шафаревич-Ремизов «Линейная алгебра и геометрия».
В целом, на русском есть много хорошей литературы, особенно на последнем уровне, но она страдает излишней сложностью.
Практика
Как и в первом случае, практика обязательна. Проходите SVD — изучите сжатие изображений. Проходите матричные умножения — изучите быстрое преобразование Фурье, алгоритм Штрассена; решайте много задач (например, из задачников Кострикина либо Проскурякова); напишите своё LU-разложение, Гаусса. Для самых упорных я могу предложить замечательные книги по численным методам линейной алгебры, такие как Trefethen, Bau «NUMERICAL LINEAR ALGEBRA»; Хорн, Джонсон «Матричный анализ». Эти книги будут полезны, во первых, для «набития» руки; во-вторых, станет сразу понятно, что многие теоретические методы разбиваются в щепки о прозу жизни (машинная точность, нестабильность методов, работа с разреженными матрицами).
Дискретная математика
Ещё один кит современной CS. Здесь нас в основном будет интересовать комбинаторика и основы теории графов.
Что нужно знать из комбинаторики и теории графов?
Биномиальные коэффициенты, их асиптотика; графы; деревья; поиск в глубину и ширину; реккурентные соотношения и их решения;
Литература
Bring it on: Андерсон Дж. «Дискретная математика и комбинаторика»; Хаггарти, Шлипф Дж., Уайтсайдс С. «Дискретная математика для программистов», Оре О. «Графы и их применение».
Две первые книги — прекрасные талмуды по дискретной математике, покрывают практически все вопросы, которые надо знать.
Hurt me plenty: Грэхем, Кнут, Паташник «Конкретная математика», Харари «Теория графов», Оре «Теория графов».
Nightmare: Сачков «Введение в комбинаторные методы дискретной математики», Омельченко «Теория графов».
Практика
Как правило, в учебники по комбинаторике включается большое количество задач; их надо прорешивать. По сути вся комбинаторика — это искусство решения различных задачек, нежели какая-то единая теория.
Комментарии (32)

old_gamer
10.12.2018 17:42Bring it on —…
Hurt me plenty —…
Nightmare —…
Сегодня им 25 лет ))
спасибо за статью, давно интересно в этом разобраться, но как-то лень, что ли…
Я так полагаю (точнее — надеюсь), предполагается цикл статей для тех, кому тоже лень самим все искать, как мне?

theCowardlyDog
10.12.2018 17:50-1Если честно, то вы не убедили меня зачем мне нужно изучать математику для ML, тем более по книгам для математиков. Вы так ратуете за утилитарность, но не привели ни одного примера, когда знание математики помогает лучше и проще решить задачу, чем перебор гиперпараметров и нагромождение ансамблей.

kirtsar Автор
10.12.2018 19:30+1Не могу ответить коротко, так что по пунктам :)
1. Я бы даже более общо ставил бы вопрос — а зачем вообще математику изучать? Математикой пичкают студентов на всех естественно-научных факультетах, и не только на них; даже психологи какие-нибудь вынуждены изучать математику. К сожалению (или к счастью?) это одно из тех немногих орудий, которое человечество имеет в своём арсенале для разгадок тайн природы.
2. Я не ставлю своей целью убедить кого-то изучать математику, поскольку невозможно в человека вложить такую чудовищной силы мотивацию извне. Математика сложная, она трудна, изучать её тяжко и энергозатратно, в жизни для многих есть более интересные занятия. Эта потребность должна идти изнутри, «почему оно так? почему не иначе?». Многими вещами я просто пользуюсь (как потребитель), к примеру, мне не очень интересно, как выращивать ананасы или персики, я их просто ем. Возможно, мне никогда не придётся этим заниматься. Я плохо разбираюсь в том, как работает медицина. Всё изучить невозможно, и надо отсеивать ненужное/неинтересное. Эта статья скорее для тех, кто хочет начать, но не знает, откуда.
3. Кто вам сказал, что это книги для математиков? Практически все книги 1-го уровня — книги для инженеров/программистов, которые исследуют математику как инструмент, а не как предмет изучения. В заглавии некоторых вообще прямым текстом написано «для программистов». Книги для математиков (уровня мехмата) — это книги 3-го уровня.
4. Где я ратую за утилитарность? Мне казалось, что я своим введением а) ясно обозначил, что математика может и не пригодиться в явном виде; б) профит, если и будет, то не сразу и не очевиден; в) в настоящей жизни «силовые» решения чаще продавливают элегантные математические.
5. Библиотеки машинного обучения (в частности, scikit и другие) часто работают хорошо за счет того, что в них уже с самого начала был заложен мощный потенциал умными людьми. Тем не менее, даже они не всегда хорошо работают из коробки. Очевидный пример: линейная регрессия на не-нормированных данных. Да и даже сам выбор модели по данным требует понимания, что теоретически может сработать, а что не «прокатит», как бы вы не подгонялись под ответ.
roryorangepants
10.12.2018 20:46Очевидный пример: линейная регрессия на не-нормированных данных.
А почему он очевидный? Ведь если ваша цель — зафитить линрег, то вы сможете сделать это и на ненормированных данных.
masai
10.12.2018 21:15Если один признак из диапазона 0..1, а второй – из 0..1000000, то решение в лоб будет намного дольше сходиться.

roryorangepants
10.12.2018 21:20Что вы называете решением в лоб?

masai
11.12.2018 13:50Подбор параметров с помощью градиентного спуска. Функция потерь будет иметь вид длинного оврага, где негде развернуться.
На точность решения через нормальное уравнение ненормированные фичи тоже плохо влияют, особенно если вычисляете псевдообратную матрицу, а не обратную.
Вот я тут проверил даже на регрессии от двух переменных. При разнице диапазонов в миллион решение через псевдобратную матрицу даёт ошибку в третьем знаке. Если нормировать, то всё OK.
Вообще, в численных методах приведение величин к одному диапазону – первое, что делают. Иначе погрешности будут зашкаливать для сколько-нибудь сложного алгоритма.
Кстати, kirtsar, я бы ещё добавил в диаграммку численные методы, раз уж о них заговорили.

roryorangepants
11.12.2018 15:27Подбор параметров с помощью градиентного спуска.
Ну так вот это не решение в лоб. Это уже нужно, когда речь идет о регуляризации. Решение в лоб именно линейной регрессии — через уравнение.
Вот я тут проверил даже на регрессии от двух переменных. При разнице диапазонов в миллион решение через псевдобратную матрицу даёт ошибку в третьем знаке. Если нормировать, то всё OK.
Расчехляю sklearn, который автор привел в пример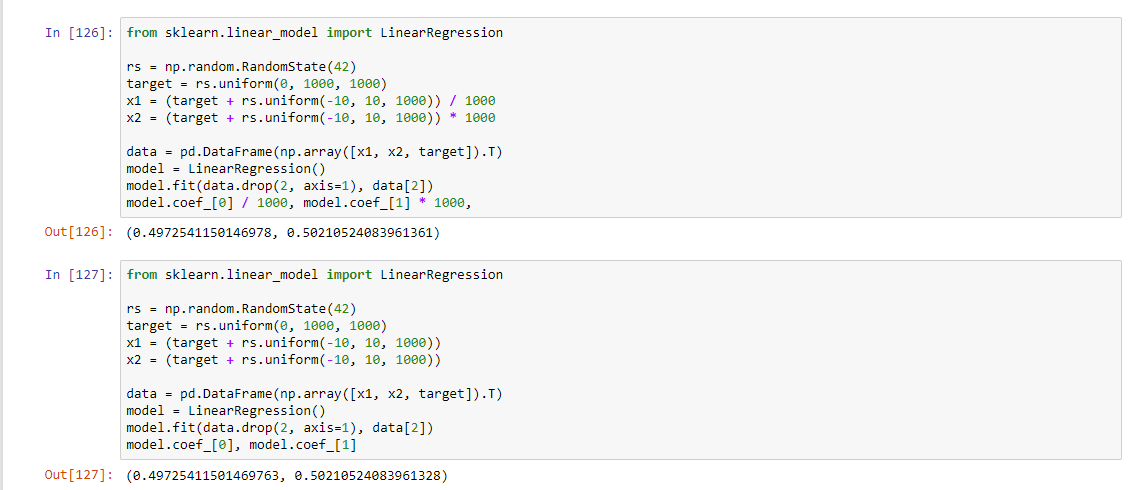
Разница в коэффициентах в тринадцатом знаке. Это реальный пример реального использования линрега в лоб на ненормированных фичах.
А вот разница в скорости работы в этом же примере:

Скорость с отнормированными фичами лучше, но в пределах погрешности.
masai
11.12.2018 20:00-1Расчехляю sklearn, который автор привел в пример
Не очень удачный пример, так как метод
fitкак раз нормализует фичи перед непосредственно вычислениями.
Поэтому у вас результаты одинаковые и получались, так как нормализация, фактически, была в обоих случаях.

roryorangepants
11.12.2018 20:54Вы бы хоть посмотрели в параметры: scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression
Нормализация по умолчанию стоит в False.
masai
12.12.2018 15:02Что ж, был невнимателен, согласен. (Впрочем,
fitцентрирует данные, так что предобработка всё же выполняется.)
Не буду спорить, что в sklearn (а точнее, его LAPACK-бэкэнде) алгоритм решения работает как надо. Но повторюсь, что если решать совсем-совсем в лоб, то масштаб влияет сильнее за счёт накопления погрешностей в алгоритмах.
Пример с псевдообратной матрицей, о котором я говорил

kirtsar Автор
11.12.2018 15:45Они там есть, только в немного суженной форме (ЧМы именно линейной алгебры, я упоминаю в «практике» к линейной алгебре + книжки). ЧМы в общем виде — это скорее всяческие сплайны, квадратуры, решение дифуров; в данном случае (машинное обучение) нужны более специфические методы (подмножество всех численных методов, которые работают именно с СЛУ).

kirtsar Автор
11.12.2018 10:02Обычно хотят ещё и коэффициенты более-менее интерпретируемые получить. С регрессией вообще не все так просто, там и статистика, и вероятность, и много линейной алгебры.

roryorangepants
11.12.2018 10:49Интепретируемые коэффициенты — это другое дело. Или, например, регуляризованная регрессия. Там мне понятно, зачем нормировать данные.
Но если вы учите простой линрег с целью получить предсказание, то вроде бы и нормировать необязательно.

S_A
11.12.2018 15:42+1Нормируют чаще всего когда работают с (объясняемой) дисперсией. PCA самый простой пример, когда на ненормированных величинах нет смысла применять.

Peacemaker
11.12.2018 11:17а зачем вообще математику изучать?
Математику уже затем изучать нужно, что она ум в порядок приводит. М.В. Ломоносов.

masai
12.12.2018 16:13Другой пример (не знаю, насколько удачный), когда надо понимать механизмы под капотом – применение линейной регрессии из sklearn «в лоб», когда фичи зависимы.

roryorangepants
10.12.2018 20:49+2когда знание математики помогает лучше и проще решить задачу, чем перебор гиперпараметров и нагромождение ансамблей.
Как вам такая теория, что нужно знать математику, чтобы разумно перебирать гиперпараметры и правильно тюнить модели в ансамбль?

gorodnev
10.12.2018 22:30А где же теор вер и статистика?
Ну и у Гилберта Стренга есть еще более практически ориентированные курсы:
А еще и книга «Computational Science and Engineering» к этим курсам.
Где бы только столько времени на это все найти…
kirtsar Автор
11.12.2018 10:09Потому и написал в заглавии, что первая часть :)
С теорвером сложно, поэтому решил отдельно вынести. Особенно с байесовским подходом — на русском вообще почти ничего не встречал, кроме упоминаний в учебниках по классической статистике.
Курсы хорошие, но там есть и такие вещи, наподобие численных решений всяческих диф. уравнений или расчёта электрических цепей. Я боюсь, что если вникать ещё и в эти (безусловно важные) области приложения линейной алгебры, то можно и не выкарабкаться никогда )) хотя наверное стоило упомянуть.

third112
11.12.2018 06:38мир не устроен по законам математики
Не слишком ли категоричное утверждение? Простейший пример для школьника: дан диаметр круглой площадки, нужно найти количество досок, чтобы сделать глухой забор по окружности. Далее можно приводить примеры из физики, которая почему-то вся на математике ;)
rai
11.12.2018 15:21Все существующие физические модели являются лишь аппроксимацией реального мира. Даже само существование точной модели вселенной не доказано, и, по моему мнению, является скорее философским вопросом.

S_A
11.12.2018 15:35Мир не устроен по законам математики
Тут слегка перевернуто с ног на голову.
- Не факт что мир вообще устроен по каким-то законам, неважно физический, экономический или химию взять,
- Тем не менее, математика призвана мир описывать, а машинное обучение как и весь data science — про то, как наблюдения (мира) собственно в саму математику уложить.
То что модели работают, пусть и не 100%, говорит о том что математика все же что-то описывает (где-то на процент своей точности), — с точки зрения математики опять же.
Но этого достаточно, чтобы например воспроизвести процесс с достаточным для употребления (персиков, ананасов и других) результатов человеком.
Тут не то чтобы курояичность, тут как бы универсальней математики у человека для работы с наблюдениями каких бы то ни было инструментов с предсказательной силой нет. С конкретно же описаниями разговорный язык лучше справляется…

third112
11.12.2018 16:46Прежде всего есть качественные закономерности, а есть количественные. Некоторые качественные закономерности являются абсолютно точными. Нпр., при нормальных условиях и достаточных в широком интервале концентрациях (можно на глазок отсыпать) водный раствор щелочи вызовет красно-фиолетовое открашивание раствора фенолфталеина.

rai
11.12.2018 17:40Вы лишь привели пример воспроизводимого эксперимента при определенном наборе начальных данных. И на его основе говорите об абсолютной точности некой закономерности. С таким таким же успехом можно наблюдать появление личинок в тухлом мясе и говорить об истиности самозарождения.

third112
11.12.2018 18:58Про личинки не знаю, не биолог. А что в моем эксперименте неточного? Где тут «лишь аппроксимация реального мира»? Или Вы предлагаете каждое точное решение называть «аппроксимация»? — ИМХО у этого термина другой смысл.

rai
11.12.2018 19:53Попытаюсь выразиться наиболее точно.
Есть физическая модель, некое решение. И есть наша действительность, о которой что-либо узнать можно лишь посредством эксперимента. Решение точно тогда и только тогда, когда для любого входного значения, результат решения равен наблюдению эксперимента. Учитывая размеры пространства и неточность измерительных приборов доказать точность решения невозможно.
third112
12.12.2018 02:18Учитывая размеры пространства и неточность измерительных приборов доказать точность решения невозможно.
Для количественных задач. А в качественной — среда щелочная или нет, т.е. без цвета или красный — высокой точности не нужно. Аналогично: какой свет на светофоре: зеленый или красный. На практике и в количественных задачах задаются разумной точностью. Так земельный участок, ограниченный окружностью диаметром 20 м, будет ограничен «не точной окружностью», нпр., где-то на см меньше, а где-то больше. И это обычно устраивает.

potan
11.12.2018 12:30Такое впечатление, что математику начали вспоминать только с ростом популярности машинного обучения. По крайней мере области, с ним не связанные, изучать ни кто не собирается.

pavlushk0
11.12.2018 13:03то чувство, когда читая статью про около математику, видишь знакомые вещи) значит усилия не проходят даром. Есть ли мнения о книге Г. Г. Харди — курс чистой математики?

KonstantinSpb
12.12.2018 14:53Пожалуй самая увесистая и охватывающая книга по линейной алгебре
Handbook of Linear Algebra
www.amazon.com/Handbook-Algebra-Discrete-Mathematics-Applications/dp/1138199893
А по матану нравится
Modern Engineering Mathematics
www.amazon.com/Modern-Engineering-Mathematics-Always-learning/dp/1292080736
Advanced Modern Engineering Mathematics
www.amazon.com/Advanced-Modern-Engineering-Mathematics-James/dp/129217434X


worldmind
del