Искажения, бесшовный шум и как с ними работать.

Один из простейших способов генерации планеты — использование шума. Если мы решим выбрать его, то у нас есть пара возможных вариантов. Давайте рассмотрим каждый и определим лучший:
Из этих трёх лично я предпочитаю Open Simplex Noise, который использую в своих личных проектах. Стоит заметить, что в текущей реализации OpenSimplexNoise для получения простого доступа к масштабу, октавам и порождающим значениям потребуется дополнительная работа. В Интернете есть множество информации о том, что делает каждый из этих элементов, и я крайне рекомендую вам её изучить. Однако в своей статье я буду говорить не об этом.

Вот как выглядит Open Simplex Noise с 16 октавами.
Шум бесконечен, а значит, если мы просто создадим холст с соотношением сторон 2:1, чтобы получить равнопромежуточную проекцию, то она не будет зацикленной при наложении на сферу (выражаю благодарность этому потрясающему веб-сайту), а на горизонтальном шве и на полюсах будут огромные отличия.
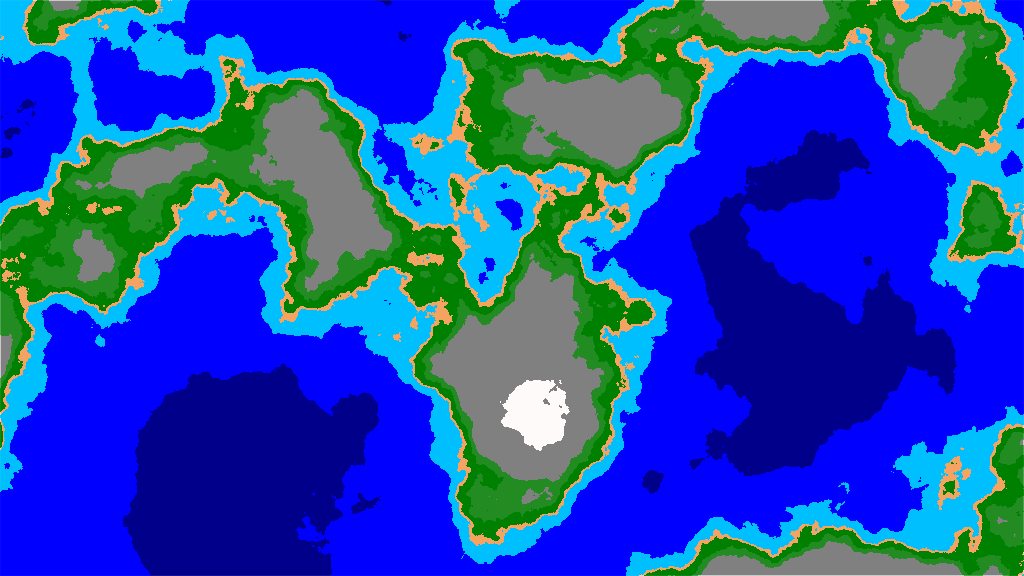
Шум, созданный без учёта швов.
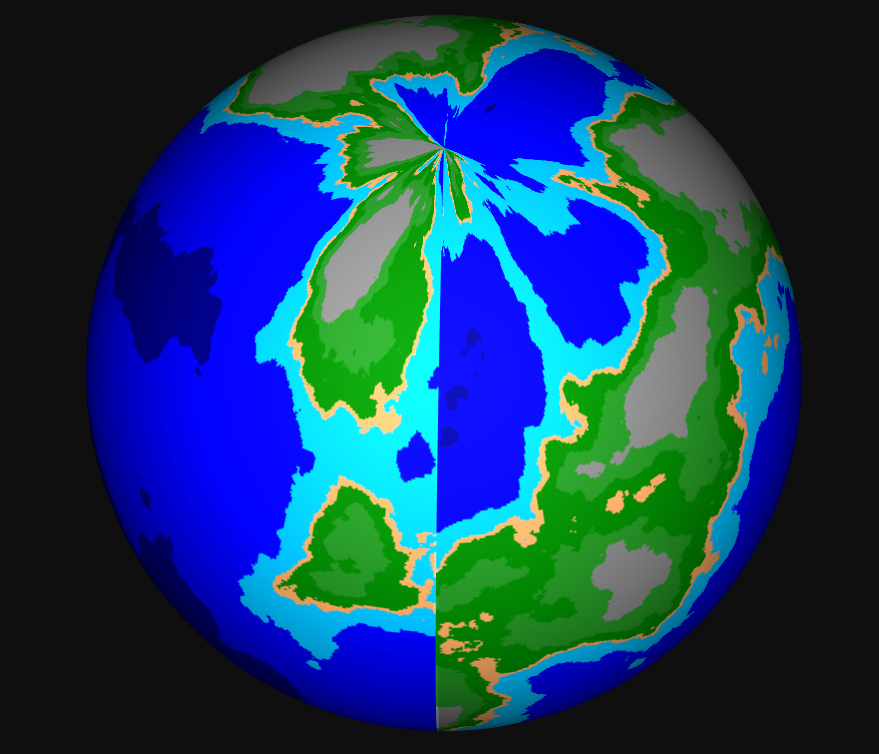
Заметьте огромные швы, появившиеся при наложении шума на сферу.
Исправить это можно множеством способов; например, в этом отличном посте Red Blob Games [перевод на Хабре] достаточно было просто сгенерировать остров с помощью функции, получающей в качестве переменной расстояние до центра и и задавая на краях высоту 0 для минимизации швов.
Однако нам нужно не это. Мы хотим сгенерировать планету с возможностью существования северного и южного полюсов, а для этого нам понадобятся более сложные математические вычисления.
Метод, способный генерировать сферические планеты, заключается в преобразовании декартовых координат нашего холста в сферические координаты, генерации шума на основании этих координат, а затем в преобразовании шума в обратно в декартовы координаты и наложении его на холст.
Однако такая реализация имеет свои ограничения, причины возникновения которых показаны в потрясающем посте Рона Валстара. Самое главное — формы континентов в этом случае выглядят чрезвычайно странными и искажёнными, а поэтому мы не будем использовать этот вариант.
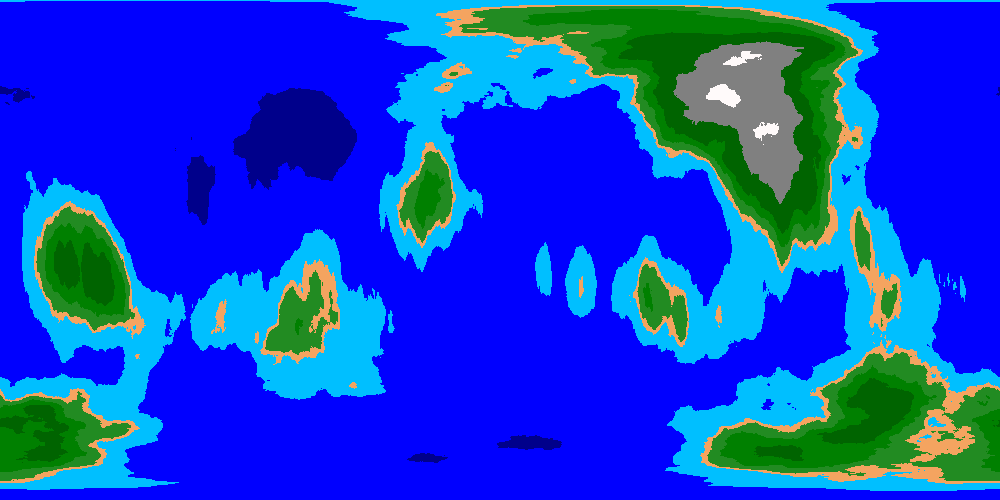
Сферическое наложение шума. Странные формы и искажения делают континенты довольно уродливыми.
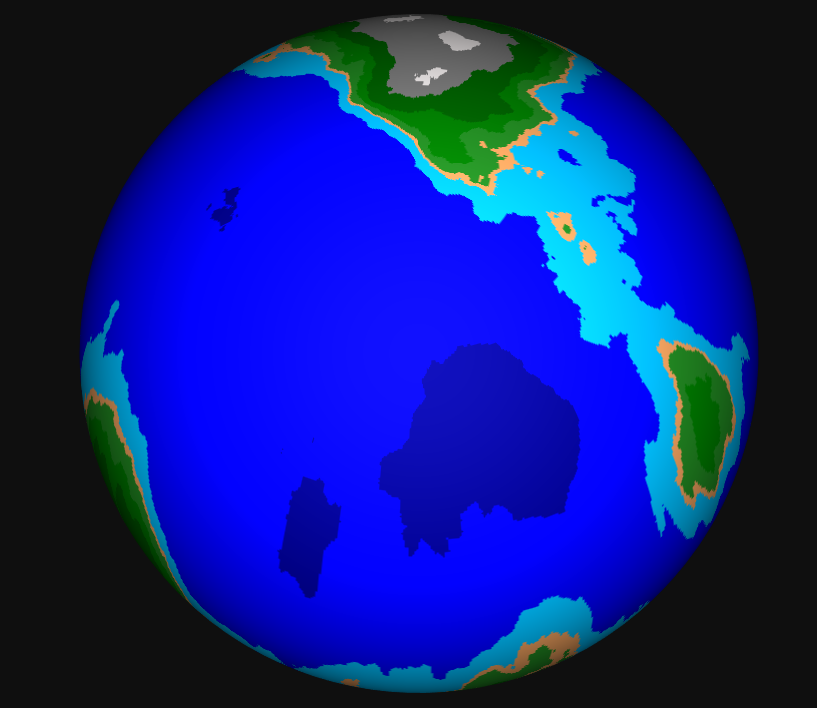
Зато, по крайней мере, швов больше нет.
В результате я использовал второй способ, взятый из поста Рона Валстара и серии статей acko Making Worlds. В них описывается генерация глобуса через генерацию куба и его «надувания», как будто он воздушный шар, до тех пор, пока он не пример форму сферы.
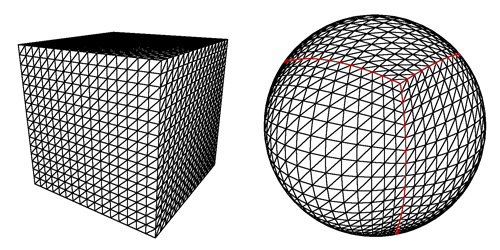
Изображение взято с acko.net. Оно объясняет концепцию кубической карты в простом для визуализации виде.
Теперь нам нужно просто сгенерировать шесть граней, что достаточно просто, есть множество способов сделать это.
В конце концов я решил создать массив и заполнить его данными. Я преобразовал 2D-координаты холста в 3D-координаты куба, а затем сгенерировал шум для каждой из этих 3D-координат так, чтобы сохранить их в соответствующее значение 2D-координаты.
Таким образом мы можем создать кубическую карту, которая легко преобразуется в равнопромежуточную проекцию с помощью замечательного кода, написанного Bartosz.

Сгенерированная алгоритмом кубическая карта.

Равнопромежуточное преобразование кубической карты.

Глобус кубической карты, отрендеренный на сайте maptoglobe.com.
Как видите, равнопромежуточная карта имеет гораздо более красивые формы, а при наложении на сферу она создаёт схожие со сферическим наложением результаты, не имея всех его недостатков. Кстати, равнопромежуточную проекцию можно легко преобразовать разными программами, например, NASA G.Projector, в практически любой тип карты.
Генерация целой планеты может показаться устрашающей задачей, и хотя шум при его правильном использовании — это довольно мощный инструмент, он имеет свои проблемы, с которыми люди сталкивались на протяжении многих веков, например, наложение глобуса на 2D-холст с минимальными искажениями.
Предложенное мной решение создаёт очень грубо сгенерированные планеты, не учитывающие тектонических плит, рек, цепочек островов и даже гор, а потому его можно использовать только в качестве демонстрации или как основу для более сложных симуляций.
На самом деле, оно создаёт только матрицу значений в определённом интервале величин. Для изображений в градациях серого это интервал 0-255. Затем значения преобразуются в пиксель, создающий изображение, схожее с первым изображением в градациях серого, или в изображение в интервале от -11000 до 8000 для симуляции разности высот реального мира, после чего пиксели окрашиваются цветами в соответствии с интервалами высот (например, значения с 0 по 5 окрашиваются в цвет песка для симуляции побережья).

Генерируем планету
Один из простейших способов генерации планеты — использование шума. Если мы решим выбрать его, то у нас есть пара возможных вариантов. Давайте рассмотрим каждый и определим лучший:
- Шум Перлина (Perlin Noise) — самый простой вариант. Шум Перлина был разработан Кеном Перлином в 1983 году, он имеет пару недостатков — визуальные артефакты и довольно низкая по сравнению с другими вариантами скорость при генерации больших изображений.
- Симплекс-шум (Simplex Noise) — разработан Кеном Перлином в 2001 году как попытка устранения недостатков шума Перлина; это вполне достойное и быстрое решение, однако обладающее серьёзным недостатком: использование трёхмерного симплекс-шума защищено патентом, что делает его довольно дорогостоящим.
- Открытый симплекс-шум (Open Simplex Noise) — был разработан KDotJPG с одной простой целью: создать современную и бесплатную версию симплекс-шума, относительно быструю и без искажений.
Из этих трёх лично я предпочитаю Open Simplex Noise, который использую в своих личных проектах. Стоит заметить, что в текущей реализации OpenSimplexNoise для получения простого доступа к масштабу, октавам и порождающим значениям потребуется дополнительная работа. В Интернете есть множество информации о том, что делает каждый из этих элементов, и я крайне рекомендую вам её изучить. Однако в своей статье я буду говорить не об этом.

Вот как выглядит Open Simplex Noise с 16 октавами.
Бесшовный шум
Шум бесконечен, а значит, если мы просто создадим холст с соотношением сторон 2:1, чтобы получить равнопромежуточную проекцию, то она не будет зацикленной при наложении на сферу (выражаю благодарность этому потрясающему веб-сайту), а на горизонтальном шве и на полюсах будут огромные отличия.

Шум, созданный без учёта швов.

Заметьте огромные швы, появившиеся при наложении шума на сферу.
Исправить это можно множеством способов; например, в этом отличном посте Red Blob Games [перевод на Хабре] достаточно было просто сгенерировать остров с помощью функции, получающей в качестве переменной расстояние до центра и и задавая на краях высоту 0 для минимизации швов.
Однако нам нужно не это. Мы хотим сгенерировать планету с возможностью существования северного и южного полюсов, а для этого нам понадобятся более сложные математические вычисления.
Сферическое наложение
Метод, способный генерировать сферические планеты, заключается в преобразовании декартовых координат нашего холста в сферические координаты, генерации шума на основании этих координат, а затем в преобразовании шума в обратно в декартовы координаты и наложении его на холст.
Однако такая реализация имеет свои ограничения, причины возникновения которых показаны в потрясающем посте Рона Валстара. Самое главное — формы континентов в этом случае выглядят чрезвычайно странными и искажёнными, а поэтому мы не будем использовать этот вариант.

Сферическое наложение шума. Странные формы и искажения делают континенты довольно уродливыми.

Зато, по крайней мере, швов больше нет.
Кубическое наложение
В результате я использовал второй способ, взятый из поста Рона Валстара и серии статей acko Making Worlds. В них описывается генерация глобуса через генерацию куба и его «надувания», как будто он воздушный шар, до тех пор, пока он не пример форму сферы.

Изображение взято с acko.net. Оно объясняет концепцию кубической карты в простом для визуализации виде.
Теперь нам нужно просто сгенерировать шесть граней, что достаточно просто, есть множество способов сделать это.
В конце концов я решил создать массив и заполнить его данными. Я преобразовал 2D-координаты холста в 3D-координаты куба, а затем сгенерировал шум для каждой из этих 3D-координат так, чтобы сохранить их в соответствующее значение 2D-координаты.
//Z STATIC
for(int y = 0; y < cubeFaceSize; y++) {
for(int x = 0; x < cubeFaceSize * 2; x++) {
//Generates FRONT
if(x < cubeFaceSize) {
cubeMap[cubeFaceSize+x][cubeFaceSize+y] = noise.noise3D(x, y, 0);
}
//Generates BACK
else {
cubeMap[cubeFaceSize*3+(x-cubeFaceSize)][cubeFaceSize+y] = noise.noise3D(cubeFaceSize-(x-cubeFaceSize), y, cubeFaceSize);
}
}
}
//X STATIC
for(int y = 0; y < cubeFaceSize; y++) {
for(int x = 0; x < cubeFaceSize * 2; x++) {
//Generates LEFT
if(x < cubeFaceSize) {
cubeMap[x][cubeFaceSize+y] = noise.noise3D(0, y, cubeFaceSize-x);
}
//Generates RIGHT
else {
cubeMap[cubeFaceSize*2+(x-cubeFaceSize)][cubeFaceSize+y] = noise.noise3D(cubeFaceSize, y, x-cubeFaceSize);
}
}
}
//Y STATIC
for(int y = 0; y < cubeFaceSize * 2; y++) {
for(int x = 0; x < cubeFaceSize; x++) {
//Generates TOP
if(y < cubeFaceSize) {
cubeMap[cubeFaceSize+x][y] = noise.noise3D(x, 0, cubeFaceSize-y);
}
//Generates BOTTOM
else {
cubeMap[cubeFaceSize+x][cubeFaceSize*2+(y-cubeFaceSize)] = noise.noise3D(x, cubeFaceSize, y-cubeFaceSize);
}
}
}Таким образом мы можем создать кубическую карту, которая легко преобразуется в равнопромежуточную проекцию с помощью замечательного кода, написанного Bartosz.

Сгенерированная алгоритмом кубическая карта.

Равнопромежуточное преобразование кубической карты.

Глобус кубической карты, отрендеренный на сайте maptoglobe.com.
Как видите, равнопромежуточная карта имеет гораздо более красивые формы, а при наложении на сферу она создаёт схожие со сферическим наложением результаты, не имея всех его недостатков. Кстати, равнопромежуточную проекцию можно легко преобразовать разными программами, например, NASA G.Projector, в практически любой тип карты.
В заключение
Генерация целой планеты может показаться устрашающей задачей, и хотя шум при его правильном использовании — это довольно мощный инструмент, он имеет свои проблемы, с которыми люди сталкивались на протяжении многих веков, например, наложение глобуса на 2D-холст с минимальными искажениями.
Предложенное мной решение создаёт очень грубо сгенерированные планеты, не учитывающие тектонических плит, рек, цепочек островов и даже гор, а потому его можно использовать только в качестве демонстрации или как основу для более сложных симуляций.
На самом деле, оно создаёт только матрицу значений в определённом интервале величин. Для изображений в градациях серого это интервал 0-255. Затем значения преобразуются в пиксель, создающий изображение, схожее с первым изображением в градациях серого, или в изображение в интервале от -11000 до 8000 для симуляции разности высот реального мира, после чего пиксели окрашиваются цветами в соответствии с интервалами высот (например, значения с 0 по 5 окрашиваются в цвет песка для симуляции побережья).
При построении Вселенной Бог использовал математику высшего уровня.
— Поль Дирак
Комментарии (7)

DrZlodberg
17.04.2019 09:02Есть ещё как минимум один вариант: использовать 3D-версию шума. Но он прокатит (впрочем, как и остальные методы) только если генерить готовую карту. Если планируется дальнейший постпроцессинг (а он необходим для реалистичной карты) то там становится всё достаточно сложно.

maquefel
17.04.2019 09:17Вот еще интересная идея:
www.gamedev.net/forums/topic/623145-terrain-generation-with-plate-tectonics

DjSapsan
18.04.2019 02:16Карта Кербина:
Как-то подозрительно похоже) Да и еще африканоподобный участок

AngReload
18.04.2019 16:54Немного не понял автора. Зачем нужно накладывать шум на куб, потом его преобразовывать… Сделал на сферу, вроде такой же результат, и при наложении на глобус в maptoglobe.com не видно искажений.
codepen.io/AngReload/full/xepLPe


heleo
Поправьте пожалуйста ссылку в
Подсвечивает адрес, но не открывается.
PatientZero Автор
Странно, у меня открывался. На всякий случай убрал из адреса #.
heleo
Спасибо! Теперь норма