В этой статье описывается библиотека optlib, предназначенная для решения задач глобальной оптимизации на языке Rust. На момент написания этой статьи в этой библиотеке реализован генетический алгоритм нахождения глобального минимума функции. Библиотека optlib не привязана к конкретному типу входных данных для оптимизируемой функции. Также библиотека построена таким образом, что при использовании генетического алгоритма можно легко менять алгоритмы скрещивания, мутации, отбора и другие этапы работы генетического алгоритма. По сути генетический алгоритм собирается как бы из кубиков.

Проблема глобальной оптимизации

Задача оптимизации обычно формулируется следующим образом.

Для некоторой заданной функции f(x) среди всех возможных значений x найти такое значение x', при котором f(x') принимает минимальное (или максимальное) значение. При этом x может принадлежать различным множествам — натуральным числам, вещественным числам, комплексным числам, векторам или матрицам.

Под экстремумом функции f(x) понимается такая точка x' , в которой производная функции f(x) равна нулю.

Существует множество алгоритмов, которые гарантированно находят экстремум функции, который является локальным минимумом или максимумом вблизи заданной начальной точки x₀. К таким алгоритмам относятся, например, алгоритмы градиентного спуска. Однако на практике часто нужно найти глобальный минимум (или максимум) функции, которая в заданном диапазоне изменения x помимо одного глобального экстремума имеет множество локальных экстремумов.

Градиентные алгоритмы не могут справиться с оптимизацией такой функции, потому что их решение сойдется к ближайшему экстремуму около начальной точки. Для задач нахождения глобального максимума или минимума используют так называемые алгоритмы глобальной оптимизации. Эти алгоритмы не гарантируют нахождение глобального экстремума, т.к. являются вероятностными алгоритмами, но ничего другого не остается кроме как пробовать различные алгоритмы применительно к конкретной задаче и смотреть, какой алгоритм лучше справится с оптимизацией, желательно за минимально возможное время и с максимальной вероятностью нахождения глобального экстремума.

Один из наиболее известных (и сложных в реализации) алгоритмов — генетический алгоритм.

Общая схема генетического алгоритма

Идея генетического алгоритма рождалась постепенно и была сформирована в конце 1960-х — начале 1970-х годов. Мощное развитие генетические алгоритмы получили после выхода книги Джона Холланда «Адаптация в естественных и искусственных системах» (1975 г.)

Генетический алгоритм основан на моделировании популяции особей на протяжении большого количества поколений. В процессе работы генетического алгоритма появляются новые особи с лучшими параметрами, а наименее удачные особи умирают. Для определенности далее перечислены термины, которые используются в генетическом алгоритме.

• Особь — одно значение x среди множества возможных значений вместе со значением целевой функции для данной точки x.
• Хромосомы — значение x.
• Хромосома — значение x_i в случае, если x является вектором.
• Функция приспособленности (фитнесс-функция, целевая функция) — оптимизируемая функция f(x).
• Популяция — совокупность особей.
• Поколение — номер итерации генетического алгоритма.

Каждая особь представляет собой одно значение x среди множества всех возможных решений. Значение оптимизируемой функции (в дальнейшем для краткости будем считать, что мы ищем минимум функции) рассчитывается для каждого значения x. Будем считать, что чем меньшее значение имеет целевая функция, тем лучше данное решение.

Генетические алгоритмы применяются во многих областях. Например, их можно использовать для подбора весовых коэффициентов в нейронных сетях. Многие CAD-системы используют генетический алгоритм для оптимизации параметров устройства, чтобы удовлетворить заданным требованиям. Также алгоритмы глобальной оптимизации можно применять для подбора расположения проводников и элементов на плате.

Структурная схема генетического алгоритма показана на следующем рисунке:

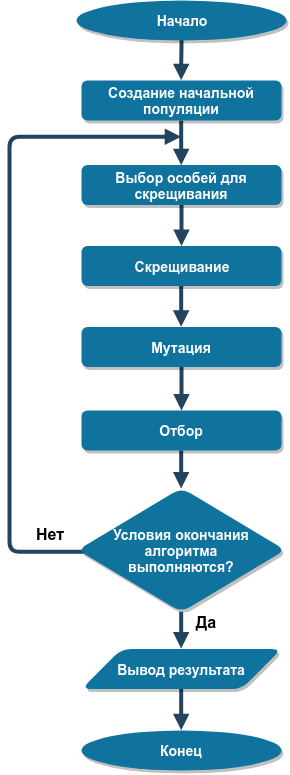
Рассмотрим каждый этап алгоритма более подробно.

Создание начальной популяции

Первый этап работы алгоритма — это создание начальной популяции, то есть создание множества особей с различными значениями хромосом x. Как правило, начальную популяцию создают из особей со случайным значением хромосом, при этом стараются, чтобы значения хромосом в популяции покрывали всю область поиска решения относительно равномерно, если нет каких-то предположений относительно того, где может находиться глобальный экстремум.

Вместо случайного распределения хромосом можно создавать хромосомы таким образом, чтобы начальные значения x были равномерно распределены по всей области поиска с заданным шагом, который зависит от того, какое количество особей будет создано на данном этапе алгоритма.

Чем больше особей будет создано на данном этапе, тем больше вероятность того, что алгоритм найдет правильное решение, а также при увеличении размера начальной популяции как правило требуется меньшее количество итераций генетического алгоритма (количество поколений). Однако при росте размера популяции требуется все большее количество расчетов целевой функции и выполнения других генетических операций на последующих этапах алгоритма. То есть при увеличении размера популяции увеличивается время расчета одного поколения.

В принципе, размер популяции не обязан оставаться постоянным на протяжении всей работы генетического алгоритма, часто по мере увеличения номера поколения размер популяции можно уменьшать, т.к. со временем все большее количество особей будут располагаться все ближе к искомому решению. Однако часто размер популяции поддерживают примерно постоянным.

Выбор особей для скрещивания

После создания популяции нужно определить, какие особи будут участвовать в операции скрещивания (см. следующий пункт). Для данного этапа существуют различные алгоритмы. Самый простой из них — скрещивать каждую особь с каждой, но тогда на следующем этапе придется выполнять слишком много операций скрещивания и расчета значений целевой функции.

Лучше дать больший шанс на скрещивание особям с более удачными хромосомами (с минимальным значением целевой функции), а тех особей, у которых целевая функция больше (хуже) лишить возможности оставить потомство.

Таким образом, на данном этапе нужно создать пары особей (или не обязательно пары, если в скрещивании могут участвовать большее количество особей), для которых на следующем этапе будет проводиться операция скрещивания.

Здесь также можно применять различные алгоритмы. Например, создавать пары случайным образом. Или можно отсортировать особей по возрастанию значению целевой функции и создавать пары из особей, расположенных ближе к началу отсортированного списка (например, из особей в первой половине списка, в первой трети списка и т.п.) Данный метод плох тем, что требуется время на сортировку особей.

Часто используется метод турнира. Когда на роль каждого претендента на скрещивание случайным образом выбирают несколько особей, среди которых в будущую пару отправляется та особь, у которой лучшее значение целевой функции. И даже здесь можно ввести элемент случайности, дав небольшой шанс особи с худшим значением целевой функции «победить» особь с лучшим значением целевой функции. Это позволяет поддерживать популяцию более разнородной, обезопасив ее от вырождения, т.е. от ситуации, когда все особи имеют примерно равные значения хромосом, что равносильно сваливанию алгоритма к одному экстремуму, возможно, не глобальному.

Результатом данной операции будет список партнеров для скрещивания.

Скрещивание

Скрещивание — это генетическая операция, в результате которой создаются новые особи с новыми значениями хромосом. Новые хромосомы создаются на основе хромосом родителей. Чаще всего в процессе скрещивания одного набора партнеров создается одна дочерняя особь, но теоретически дочерних особей может создаваться больше.

Алгоритм скрещивания также можно реализовать разными способами. Если у особей тип хромосом — число, то самое простое, что можно сделать, это создать новую хромосому как среднее арифметическое или среднее геометрическое от хромосом родителей. Для многих задач этого достаточно, но чаще всего применяют другие алгоритмы на основе битовых операций.

Побитовое скрещивание работает таким образом, что дочерняя хромосома состоит из части бит одного родителя и части бит другого родителя, как показано на следующем рисунке:

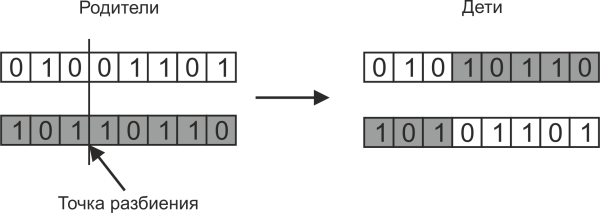
Точка разбиения родителей обычно выбирается случайным образом. Не обязательно при таком скрещивании создавать два ребенка, часто ограничиваются одним из них.

Если точка разбиения родительских хромосом одна, то такое скрещивание называется одноточечным. Но можно использовать и многоточечное разбиение, когда хромосомы родителей разбиваются на несколько участков, как показано на следующем рисунке:

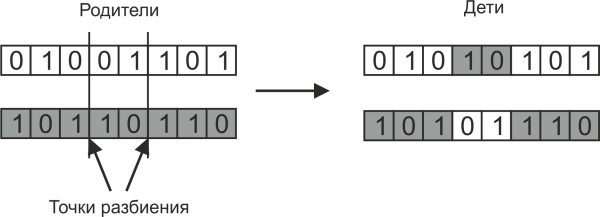
В этом случае возможно больше комбинаций дочерних хромосом.

Если хромосомы представляют собой числа с плавающей точкой, то к ним можно применять все описанные выше способы, но они будут не очень эффективны. Например, если числа с плавающей точкой скрещивать побитово, как было описано ранее, то многие операции скрещивания будут создавать дочерние хромосомы, которые будут отличны от одного из родителей только лишь в дальнем знаке после запятой. Ситуация особенно усугубляется, если использовать числа с плавающей точкой двойной точности.

Для решения этой проблемы нужно напомнить, что числа с плавающей точкой согласно стандарту IEEE 754 хранятся в виде трех чисел целых чисел: S (один бит), M и N, из которых рассчитывается число с плавающей точкой как x = (-1)^S?M?2^N. Один из способов скрещивания чисел с плавающей точкой состоит в том, чтобы сначала разбить число на составляющие S, M, N, которые представляют собой целые числа, а затем к числам M и N применить побитовые операции скрещивания, описанные выше, выбрать знак S одного из родителей, и из полученных значений составить дочернюю хромосому.

Во многих задачах особь имеет не одну, а несколько хромосом, причем может быть даже разных типов (целые и числа с плавающей точкой). Тогда возникает еще больше вариантов скрещивания таких хромосом. Например, при создании дочерней особи можно скрещивать все хромосомы родителей, а можно некоторые хромосомы полностью передавать от одного из родителей без изменений.

Мутация

Мутация — важный этап генетического алгоритма, который поддерживает разнообразие хромосом особей и таким образом уменьшает шансы на то, что решение быстро сойдется к какому-то локальному минимуму вместо глобального. Мутация представляет собой случайное изменение в хромосоме особи, которая была только что создана путем скрещивания.

Как правило, вероятность мутации устанавливается не очень большой, чтобы мутация не мешала сходимости алгоритма, иначе она будет портить особи с удачными хромосомами.

Так же как и для скрещивания, для мутации можно использовать разные алгоритмы. Например, можно заменять одну хромосому или несколько хромосом на случайную величину. Но чаще всего используют побитовую мутацию, когда в хромосоме (или в нескольких хромосомах) инвертируют один бит или несколько битов, как показано на следующих рисунках.

Мутация одного бита:

Мутация нескольких битов:

Количество бит для мутации может либо заранее задаваться, либо быть случайной величиной.

В результате мутации особи могут получиться как более удачные, так и менее удачные, но эта операция позволяет с ненулевой вероятностью появиться удачной хромосоме с наборами нулей и единиц, которых не было у родительских особей.

Отбор

В результате скрещивания и последующей мутации появляются новые особи. Если бы не существовало этапа отбора, то количество особей росло бы по экспоненциальному закону, что требовало бы все большего количества оперативной памяти и времени на обработку каждого нового поколения популяции. Поэтому после появления новых особей нужно очистить популяцию от наименее удачных особей. Именно это происходит на этапе отбора.

Алгоритмы отбора также могут быть различные. Часто в первую очередь отбрасываются особи, чьи хромосомы не попадают в заданный интервал поиска решения.

Затем можно отбросить такое количество наименее удачных особей, чтобы поддерживать постоянный размер популяции. Также могут применяться различные вероятностные критерии для отбора, например, вероятность отбора особи может зависеть от значения целевой функции.

Условия окончания алгоритма

Так же как и в других этапах генетического алгоритма, существует несколько критериев окончания алгоритма.

Самый простой критерий окончания алгоритма заключается в том, чтобы прервать алгоритм после заданного номера итерации (поколения). Но этот критерий нужно использовать осторожно, потому что генетический алгоритм является вероятностным, и разные запуски алгоритма могут сходиться с разной скоростью. Обычно критерий окончания по номеру итерации используют как дополнительный критерий на случай, если алгоритму не удается найти решение в течение большого количества итераций. Поэтому в качестве порога номера итерации нужно задавать достаточно большое число.

Другой критерий останова заключается в том, что алгоритм прерывается, если на протяжении заданного числа итераций не появляется новое лучшее решение. Это значит, что алгоритм нашел глобальный экстремум или застрял в локальном экстремуме.

Также существует неблагоприятная ситуация, когда хромосомы всех особей имеют одно и то же значение. Это так называемая вырожденная популяция. Скорее всего в этом случае алгоритм застрял в одном экстремуме, и не обязательно глобальном. Вывести популяцию из такого состояния способна только удачная мутация, но поскольку вероятность мутации обычно устанавливают небольшой, и далеко не факт, что мутация создаст более удачную особь, то обычно ситуация с вырожденной популяцией рассматривается как повод остановить генетический алгоритм. Для проверки такого критерия нужно сравнить хромосомы всех особей, есть ли среди них различия, и если различий нет, то остановить алгоритм.

В некоторых задачах не требуется нахождения глобального минимума, а нужно найти достаточно хорошее решение — решение, значение целевой функции для которого меньше заданной величины. В этом случае алгоритм можно остановить досрочно, если найденное на очередной итерации решение удовлетворяет данному критерию.

optlib

Optlib — это библиотека для языка Rust, предназначенная для оптимизации функций. На момент написания этих строк в библиотеке реализован только генетический алгоритм, но в будущем планируется расширять эту библиотеку, добавляя в нее новые алгоритмы оптимизации. Optlib полностью написана на Rust.

Optlib — библиотека с открытым кодом, она распространяется под лицензией MIT.

• Страница на github — https://github.com/Jenyay/rust-optimization
• Страница на crates.io — https://crates.io/crates/optlib
• Документация — https://docs.rs/optlib

optlib::genetic

Из описания генетического алгоритма видно, что многие этапы алгоритма можно реализовать по-разному, подбирая их таким образом, чтобы для данной целевой функции алгоритм сходился к правильному решению за минимальное количество времени.

Модуль optlib::genetic создан таким образом, чтобы можно было собирать генетический алгоритм «из кубиков». При создании экземпляра структуры, внутри которой будет происходить работа генетического алгоритма, нужно указать, какие алгоритмы будут использоваться для создания популяции, выбора партнеров, скрещивания, мутации, отбора, а также какой критерий используется для прерывания алгоритма.

В библиотеке уже существуют наиболее часто используемые алгоритмы этапов генетического алгоритма, но можно создавать и свои типы, реализующие соответствующие алгоритмы.

В библиотеке наиболее хорошо проработан случай, когда хромосомы — это вектор дробных чисел, т.е. когда минимизируется функция f(x), где x — это вектор чисел с плавающей точкой (f32 или f64).

Пример оптимизации с использованием optlib::genetic

Прежде чем начать подробно описывать модуль genetic, рассмотрим пример его использования для минимизации функции Швефеля (Schwefel function). Эта многомерная функция рассчитывается следующим образом:

$$

Минимум функции Швефеля на интервале -500 <= x_i <= 500 расположен в точке x' , где все x_i = 420.9687 для i = 1, 2, ..., N, а значение функции в этой точке f(x' ) = 0.

Если N = 2, то трехмерное изображение этой функции выглядит следующим образом:

Экстремумы видны более наглядно, если построить линии уровня этой функции:

Следующий пример показывает как с помощью модуля genetic найти минимум функции Швефеля. Этот пример вы можете найти в исходных кодах в папке examples/genetic-schwefel.

//! Пример оптимизации функции Швефеля.
//!
//! y = f(x), где x = (x0, x1, ..., xi,... xn).
//! Глобальный минимум находится в точке x' = (420.9687, 420.9687, ...)
//! Интервал поиска решения для всех xi - [-500.0; 500.0].
//! f(x') = 0
//!
//! # Термины
//! * `Целевая функция` - Функция для оптимизации. y = f(x).
//! * `Хромосомы` - точка в пространстве поиска, x = (x0, x1, x2, ..., xn).
//! * `Особь` - совокупность хромосом x и значения целевой функции.
//! * `Популяция` - набор особей.
//! * `Поколение` - номер итерации генетического алгоритма.
use optlib::genetic;
use optlib::genetic::creation;
use optlib::genetic::cross;
use optlib::genetic::goal;
use optlib::genetic::logging;
use optlib::genetic::mutation;
use optlib::genetic::pairing;
use optlib::genetic::pre_birth;
use optlib::genetic::selection;
use optlib::genetic::stopchecker;
use optlib::testfunctions;
use optlib::Optimizer;

/// Тип одной хромосомы
type Gene = f32;

/// Тип хромосомы
type Chromosomes = Vec<Gene>;

fn main() {
    // Основные параметры

    // Пространство поиска. Все xi должны лежать на отрезке [-500.0; 500.0]
    let minval: Gene = -500.0;
    let maxval: Gene = 500.0;

    // Колиество особей в начальной популяции
    let population_size = 500;

    // Количество хромосом xi в особи. 
	// Оптимизируется 15-мерная функция Швефеля
    let chromo_count = 15;

    let intervals = vec![(minval, maxval); chromo_count];

    // Создание объекта для целевой функции (функции Швефеля)
	// Функция Швефеля включена в модуль optlib::testfunctions
    let goal = goal::GoalFromFunction::new(testfunctions::schwefel);

    // Создание объекта создателя для заполнения начальной популяции.
    // RandomCreator будет создавать случайные хромосомы в заданном интервале.
    let creator = creation::vec_float::RandomCreator::new(population_size, intervals.clone());

    // Создание объекта для выбора партнеров для скрещивания
    // Выбор партнеров по методу турнира.
    let partners_count = 2;
    let families_count = population_size / 2;
    let rounds_count = 5;
    let pairing = pairing::Tournament::new(partners_count, families_count, rounds_count);

    // Алгоритм скрещивания
    // Создание объекта для побитового скрещивания ген,
    // тип которых - числа с плавающей точкой
    let single_cross = cross::FloatCrossExp::new();
    let cross = cross::VecCrossAllGenes::new(Box::new(single_cross));

    // Создание объекта мутации
    // Использовать побитовую мутацию (изменение случайных бит с заданной вероятностью).
    let mutation_probability = 15.0;
    let mutation_gene_count = 3;
    let single_mutation = mutation::BitwiseMutation::new(mutation_gene_count);
    let mutation = mutation::VecMutation::new(mutation_probability, Box::new(single_mutation));

    // Предрождение. На этом этапе можно удалить новые хромосомы,
	// которые не удовлетворяют условиям задачи.
    let pre_births: Vec<Box<genetic::PreBirth<Chromosomes>>> = vec![Box::new(
        pre_birth::vec_float::CheckChromoInterval::new(intervals.clone()),
    )];

    // Критерий останова алгоритма
	// Алгоритм будет остановлен, если значение целевой функции станет меньше 1e-4
	// или после 3000 поколения (итерации).
    let stop_checker = stopchecker::CompositeAny::new(vec![
        Box::new(stopchecker::Threshold::new(1e-4)),
        Box::new(stopchecker::MaxIterations::new(3000)),
    ]);

	// Создание объекта для отбора. Отбор - уничтожение худших особей.
	// Будут уничтожены особи со значением целевой функции NaN или Inf.
	// Будут уничтожены худшие особи, чтобы поддерживать постоянный размер популяции.
    let selections: Vec<Box<dyn genetic::Selection<Chromosomes>>> = vec![
        Box::new(selection::KillFitnessNaN::new()),
        Box::new(selection::LimitPopulation::new(population_size)),
    ];

    // Создание объектов для ведения логов.
	// Один объект будет показывать результат работы алгоритма,
	// Второй объект будет измерять время работы алгоритма.
    let loggers: Vec<Box<genetic::Logger<Chromosomes>>> = vec![
        Box::new(logging::StdoutResultOnlyLogger::new(15)),
        Box::new(logging::TimeStdoutLogger::new()),
    ];

    // Создание основной структуры оптимизатора
    let mut optimizer = genetic::GeneticOptimizer::new(
        Box::new(goal),
        Box::new(stop_checker),
        Box::new(creator),
        Box::new(pairing),
        Box::new(cross),
        Box::new(mutation),
        selections,
        pre_births,
        loggers,
    );

    // Запуск генетического алгоритма
    optimizer.find_min();
}

Этот пример можно запустить из корня исходников, выполнив команду

cargo run --bin genetic-schwefel --release

Результат работы должен выглядеть примерно так:

Solution:
  420.962615966796875
  420.940093994140625
  420.995391845703125
  420.968505859375000
  420.950866699218750
  421.003784179687500
  421.001281738281250
  421.300537109375000
  421.001708984375000
  421.012603759765625
  420.880493164062500
  420.925079345703125
  420.967559814453125
  420.999237060546875
  421.011505126953125

Goal: 0.015625000000000
Iterations count: 3000
Time elapsed: 2617 ms

Большая часть кода примера занимает создание объектов типажей для различных этапов генетического алгоритма. Как было написано в начале статьи, каждый этап генетического алгоритма может быть реализован различными способами. Для использования модуля optlib::genetic нужно создать объекты типажей, которые реализуют каждый этап тем или иным способом. Затем все эти объекты передаются в конструктор структуры GeneticOptimizer, внутри которой реализован генетический алгоритм.

Метод find_min() структуры GeneticOptimizer запускает выполнение генетического алгоритма.

Основные типажи и объекты

Базовые типажи модуля optlib

Библиотека optlib разрабатывалась с прицелом на то, что в будущем будут добавляться новые алгоритмы оптимизации, причем таким образом, чтобы в программе можно было бы легко переключаться с одного алгоритма оптимизации на другой, поэтому модуль optlib содержит типаж Optimizer, который включает в себя единственный метод — find_min(), запускающий алгоритм оптимизации на выполнение. Здесь тип T — это тип объекта, представляющего собой точку в пространстве поиска решения. Например, в приведенном выше примере — это Vec<Gene> (где Gene — псевдоним для f32). То есть это тот тип, объект которого подается на вход целевой функции.

Типаж Optimizer объявлен в модуле optlib следующим образом:

pub trait Optimizer<T> {
    fn find_min(&mut self) -> Option<(&T, f64)>;
}

Метод find_min() типажа Optimizer должен вернуть объект типа Option<(&T, f64)>, где &T в возвращаемом кортеже — это найденное решение, а f64 — значение целевой функции для найденного решения. Если же алгоритм не смог найти решение, то функция find_min() должна вернуть None.

Поскольку многие стохастические алгоритмы оптимизации используют так называемых агентов (в терминах генетического алгоритма агент — это особь), то модуль optlib также содержит типаж AlgorithmWithAgents с единственным методом get_agents(), который должен возвращать вектор агентов.

Агент, в свою очередь, — это структура, которая реализует еще один типаж из optlib — Agent.

Типажи AlgorithmWithAgents и Agent объявлены в модуле optlib следующим образом:

pub trait AlgorithmWithAgents<T> {
    type Agent: Agent<T>;

    fn get_agents(&self) -> Vec<&Self::Agent>;
}

pub trait Agent<T> {
    fn get_parameter(&self) -> &T;
    fn get_goal(&self) -> f64;
}

И для AlgorithmWithAgents, и для Agent тип T имеет то же значение, что и для Optimizer, то есть это тип объекта, для которого рассчитывается значение целевой функции.

Структура GeneticOptimizer — реализация генетического алгоритма

Для структуры GeneticOptimizer реализованы оба типажа — Optimizer и AlgorithmWithAgents.

Каждый этап генетического алгоритма представлен своим типажом, который можно реализовать с нуля или воспользоваться одной из имеющихся внутри optlib::genetic реализаций. Для каждого этапа генетического алгоритма внутри модуля optlib::genetic есть подмодуль со вспомогательными структурами и функциями, которые реализуют наиболее часто используемые алгоритмы этапов генетического алгоритма. Про эти модули будет сказано ниже. Также внутри некоторых таких подмодулей существует подмодуль vec_float, реализующие этапы алгоритма для случая, если целевая функция рассчитывается от вектора чисел с плавающей точкой (f32 или f64).

Конструктор структуры GeneticOptimizer объявлен следующим образом:

impl<T: Clone> GeneticOptimizer<T> {
    pub fn new(
        goal: Box<dyn Goal<T>>,
        stop_checker: Box<dyn StopChecker<T>>,
        creator: Box<dyn Creator<T>>,
        pairing: Box<dyn Pairing<T>>,
        cross: Box<dyn Cross<T>>,
        mutation: Box<dyn Mutation<T>>,
        selections: Vec<Box<dyn Selection<T>>>,
        pre_births: Vec<Box<dyn PreBirth<T>>>,
        loggers: Vec<Box<dyn Logger<T>>>,
    ) -> GeneticOptimizer<T> {
        ...
    }
    ...
}

Конструктор GeneticOptimizer принимает множество объектов-типажей, которые влияют на каждый этап работы генетического алгоритма, а также на вывод результатов работы:

• goal: Box<dyn Goal<T>> — целевая функция;
• stop_checker: Box<dyn StopChecker<T>> — критерий останова;
• creator: Box<dyn Creator<T>> — создание начальной популяции;
• pairing: Box<dyn Pairing<T>> — алгоритм выбора партнеров для скрещивания;
• cross: Box<dyn Cross<T>> — алгоритм скрещивания;
• mutation: Box<dyn Mutation<T>> — алгоритм мутации;
• selections: Vec<Box<dyn Selection<T>>> — вектор алгоритмов отбора;
• pre_births: Vec<Box<dyn PreBirth<T>>> — вектор алгоритмов уничтожения неудачных хромосом до создания особей;
• loggers: Vec<Box<dyn Logger<T>>> — вектор объектов, сохраняющих лог работы генетического алгоритма.

Для запуска алгоритма нужно выполнить метод find_min() типажа Optimizer. Помимо этого в структуре GeneticOptimizer имеется метод next_iterations(), который можно использовать для продолжения расчета после завершения работы метода find_min().

Иногда после останова алгоритма полезно изменить параметры алгоритма или используемые методы. Это можно сделать с помощью следующих методов структуры GeneticOptimizer: replace_pairing(), replace_cross(), replace_mutation(), replace_pre_birth(), replace_selection(), replace_stop_checker(). Эти методы позволяют заменить типажи-объекты, переданные структуре GeneticOptimizer при ее создании.

Основные типажи для генетического алгоритма рассматриваются в следующих разделах.

Типаж Goal — целевая функция

Типаж Goal объявлен в модуле optlib::genetic следующим образом:

pub trait Goal<T> {
    fn get(&self, chromosomes: &T) -> f64;
}

Метод get() должен возвращать значение целевой функции для заданной хромосомы.

Внутри модуля optlib::genetic::goal содержится структура GoalFromFunction, которая реализует типаж Goal. Для этой структуры есть конструктор, принимающий функцию, которая является целевой функцией. То есть с помощью этой структуры можно создавать типаж-объект Goal из обычной функции.

Типаж Creator — создание начальной популяции

Типаж Creator описывает «создателя» начальной популяции. Этот типаж объявлен следующим образом:

pub trait Creator<T: Clone> {
    fn create(&mut self) -> Vec<T>;
}

Метод create() должен возвращать вектор хромосом, на основе которых будет создана начальная популяция.

Для случая, если оптимизируется функция от нескольких чисел с плавающей точкой, в модуле optlib::genetic::creator::vec_float есть структура RandomCreator<G> для создания начального распределения хромосом случайным образом.

Здесь и далее тип <G> представляет собой тип одной хромосомы в векторе хромосом (иногда вместо термина «хромосома» используют термин «ген»). В основном под типом <G> будет подразумеваться тип f32 или f64 в случае, если хромосомы — это тип Vec<f32> или Vec<f64>.

Структура RandomCreator<G> объявлена следующим образом:

pub struct RandomCreator<G: Clone + NumCast + PartialOrd> {
    ...
}

Здесь NumCast — это типаж из крейта num. Этот типаж позволяет создавать тип из других числовых типов с помощью метода from().

Чтобы создать структуру RandomCreator<G>, нужно воспользоваться функцией new(), которая объявлена следующим образом:

pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> {
    ...
}

Здесь population_size — размер популяции (количество наборов хромосом, которое нужно создать), а intervals — это вектор кортежей из двух элементов — минимальным и максимальным значением соответствующей хромосомы (гена) в наборе хромосом, а размер этого вектора определяет сколько хромосом содержится в наборе хромосом у каждой особи.

В примере, приведенном выше, оптимизировалась функция Швефеля для 15 переменных типа f32. Каждая переменная должна лежать в интервале [-500; 500]. То есть для создания популяции вектор interval должен содержать 15 кортежей (-500.0f32, 500.0f32).

Типаж Pairing — выбор партнеров для скрещивания

Типаж Pairing используется для выбора особей, которые будут скрещиваться между собой. Этот типаж объявлен следующим образом:

pub trait Pairing<T: Clone> {
    fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>;
}

Метод get_pairs() заимствует указатель на структуру Population, которая содержит в себе все особи популяции, а также через эту структуру можно узнать лучшую и худшую особь в популяции.

Метод get_pairs() типажа Pairing должен вернуть вектор, который содержит вектора, которые хранят индексы особей, которые будут скрещиваться между собой. В зависимости от алгоритма скрещивания (о них будет сказано в следующем разделе) скрещиваться могут две и более особи.

Например, если будут скрещиваться особи с индексом 0 и 10, 5 и 2, 6 и 3, то метод get_pairs() должен вернуть вектор vec![vec![0, 10], vec![5, 2], vec![6, 3]].

Модуль optlib::genetic::pairing содержит две структуры, реализующие различные алгоритмы выбора партнеров.

Для структуры RandomPairing реализован типаж Pairing таким образом, что для скрещивания партнеры выбираются случайным образом.

Для структуры Tournament типаж Pairing реализован таким образом, чтобы использовался метод турнира. Метод турнира подразумевает, что каждая особь, которая будет участвовать в скрещивании, должна победить другую особь (значение целевой функции победившей особи должно быть меньше). Если в методе турнира используется один раунд, это значит, что случайным образом выбираются две особи, и в будущую «семью» попадает особь с меньшим значением целевой функции среди этих двух особей. Если используется несколько раундов, то победившая особь таким образом должна выиграть у нескольких случайных особей.

Конструктор структуры Tournament объявлен следующим образом:

pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament {
	...
}

Здесь:

• partners_count — необходимое количество особей для скрещивания;
• families_count — количество «семей», т.е. наборов особей, которые будут порождать потомство;
• rounds_count — количество раундов в турнире.

В качестве дальнейшей модификации метода турнира можно использовать генератор случайных чисел, чтобы дать небольшой шанс победить особи с худшим значением целевой функции, т.е. сделать так, чтобы на вероятность победы влияло значение целевой функции, и чем больше разница между двумя конкурентами, тем больше шансов победить у лучшей особи, а при почти равных значениях целевой функции вероятность победы одной особи была бы близка к 50%.

Типаж Cross — скрещивание

После того, как были сформированы «семьи» из особей, для скрещивания, нужно скрестить их хромосомы, чтобы получить детей с новыми хромосомами. Этап скрещивания представлен типажом Cross, который объявлен следующим образом:

pub trait Cross<T: Clone> {
    fn cross(&mut self, parents: &[&T]) -> Vec<T>;
}

Метод cross() выполняет скрещивание одного набора родителей. Этот метод принимает параметр parents — срез из ссылок на хромосомы родителей (не сами особи) — и должен вернуть вектор из новых хромосом. Размер parents зависит от алгоритма выбора партнеров для скрещивания с помощью типажа Pairing, который был описан в предыдущем разделе. Часто используется алгоритм, который создает новые хромосомы на основе хромосом из двух родителей, тогда размер parents будет равен двум.

В модуле optlib::genetic::cross содержатся структуры, для которых реализован типаж Cross с разными алгоритмами скрещивания.

• VecCrossAllGenes — структура, предназначенная для скрещивания хромосом, когда у каждой особи набор хромосом — это вектор. Конструктор VecCrossAllGenes принимает типаж-объект Cross, который будет применен для всех элементов векторов родительских хромосом. В этом случае размеры векторов хромосом родителей должны быть одного размера. В приведенном выше примере используется структура VecCrossAllGenes, потому что хромосома в используемых особях — это тип Vec<f32>.
• CrossMean — структура, которая скрещивает два числа таким образом, что в качестве дочерней хромосомы будет число, рассчитанное как среднее арифметическое от родительских хромосом.
• FloatCrossGeometricMean — структура, которая скрещивает два числа таким образом, что в качестве дочерней хромосомы будет число, рассчитанное как среднее геометрическое от родительских хромосом. В качестве хромосом должны быть числа с плавающей точкой.
• CrossBitwise — побитовое одноточечное скрещивание двух чисел.
• FloatCrossExp — побитовое одноточечное скрещивание чисел с плавающей точкой. Независимо скрещиваются мантиссы и экспоненты родителей. Знак ребенок получает от одного из родителей.

Также в модуле optlib::genetic::cross содержатся функции для побитового скрещивания чисел разного типа — целочисленных и с плавающей точкой.

Типаж Mutation — мутация

После скрещивания необходимо провести мутацию полученных детей, чтобы поддерживать разнообразие хромосом, и популяция не скатилась к вырожденному состоянию. Для популяции предназначен типаж Mutation, который объявлен следующим образом:

pub trait Mutation<T: Clone> {
    fn mutation(&mut self, chromosomes: &T) -> T;
}

Единственный метод mutation() типажа Mutation заимствует ссылку на хромосому и должен вернуть возможно измененную хромосому. Как правило, устанавливают небольшую вероятность мутации, например, единицы процентов, чтобы все-таки сохранялись хромосомы, полученные на основе родителей и таким образом улучшали популяцию.

Некоторые алгоритмы мутации уже реализованы в модуле optlib::genetic::mutation.

В этом модуле, например, содержится структура VecMutation, которая работает аналогично структуре VecCrossAllGenes, т.е. в случае если хромосома — это вектор, VecMutation принимает типаж-объект Mutation и применяет его с заданной вероятностью для всех элементов вектора, создавая новый вектор с мутированными генами (элементами вектора-хромосомы).

Также в модуле optlib::genetic::mutation содержится структура BitwiseMutation, для которой реализован типаж Mutation. Эта структура инвертирует заданное количество случайных бит в переданной ей хромосоме. Эту структуру целесообразно использовать вместе со структурой VecMutation.

Типаж PreBirth — отбор перед рождением

После скрещивания и мутации обычно наступает этап отбора, на котором уничтожаются самые неудачные особи. Однако в реализации генетического алгоритма в библиотеке optlib::genetic перед этапом отбора есть еще один этап, на котором можно отбросить неудачные хромосомы. Этот этап был добавлен, потому что расчет целевой функции для особей часто занимает достаточно много времени, и незачем ее рассчитывать, если хромосомы не попадают в заведомо известный интервал поиска. Например, в приведенном выше примере должны быть отброшены хромосомы, которые не попадают на отрезок [-500; 500].

Для выполнения такой предварительной фильтрации предназначен типаж PreBirth, который объявлен следующим образом:

pub trait PreBirth<T: Clone> {
    fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>);
}

Единственный метод pre_birth() типажа PreBirth заимствует ссылку на упоминаемую выше структуру Population, а также изменяемую ссылку на вектор хромосом new_chromosomes. Это вектор хромосом, полученных после этапа мутации. Реализация метода pre_birth() должна удалить из этого вектора те хромосомы, которые заведомо не подходят по условию задачи.

Для случая, если оптимизируется функция от вектора чисел с плавающей точкой, в модуле optlib::genetic::pre_birth::vec_float содержится структура CheckChromoInterval, предназначенная для удаления хромосом, если они представляют собой вектор чисел с плавающей точкой, и какой-нибудь элемент вектора не попадает в заданный интервал.

Конструктор структуры CheckChromoInterval выглядит следующим образом:

pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> {
        ...
    }

Здесь конструктор принимает вектор кортежей с двумя элементами — минимальным и максимальным значением для каждого элемента в хромосоме. Таким образом, размер вектора intervals должен совпадать с размером вектора-хромосомы особей. В приведенном выше примере в качестве intervals использовался вектор из 15 кортежей (-500.0f32, 500.0f32).

Типаж Selection — отбор

После предварительного отбора хромосом создаются особи и помещаются в популяцию (структуру Population). В процессе создания особей для каждой из них рассчитывается значение целевой функции. На этапе отбора нужно уничтожить некоторое количество особей, чтобы популяция не разрасталась бесконечно. Для этого используется типаж Selection, который объявлен следующим образом:

pub trait Selection<T: Clone> {
    fn kill(&mut self, population: &mut Population<T>);
}

Объект, который реализует типаж Selection, в методе kill() должен вызвать метод kill() структуры Individual (особь) для каждой особи в популяции, которую нужно уничтожить.

Для обхода всех особей в популяции можно воспользоваться итератором, который возвращает метод IterMut() структуры Population.

Поскольку часто нужно применять несколько критериев отбора, то при создании структуры GeneticOptimizer, конструктор принимает вектор типажей-объектов Selection.

Как и с другими этапами генетического алгоритма, в модуле optlib::genetic::selection уже предлагается несколько реализаций этапа отбора.

• KillFitnessNaN — уничтожает особи, у которых значение целевой функции равно NaN или Inf.
• LimitPopulation — уничтожает такое количество худших особей, чтобы размер популяции не превышал заданного размера.
• optlib::genetic::selection::vec_float::CheckChromoInterval — для случая, если оптимизируется функция от вектора чисел с плавающей точкой, уничтожает особей, значение хромосом которых не укладывается в заданные интервалы. Эта структура работает аналогично структуре optlib::genetic::pre_birth::vec_floatCheckChromoInterval предыдущего этапа генетического алгоритма.

Типаж StopChecker — критерий останова

После этапа отбора нужно проверить, не пора ли останавливать генетический алгоритм. Как уже писалось выше, на этом этапе также можно использовать различные алгоритмы останова. За прерывание алгоритма отвечает объект, для которого реализован типаж StopChecker, который объявлен следующим образом:

pub trait StopChecker<T: Clone> {
    fn can_stop(&mut self, population: &Population<T>) -> bool;
}

Здесь метод can_stop() должен вернуть true, если алгоритм можно останавливать, в противном случае этот метод должен вернуть false.

Модуль optlib::genetic::stopchecker содержит несколько структур с базовыми критериями останова и две структуры для создания комбинаций из других критериев:

• MaxIterations — критерий останова по номеру поколения. Генетический алгоритм остановится после заданного количества итераций (поколений).
• GoalNotChange — критерий останова, согласно которому алгоритм должен остановиться, если на протяжении заданного количества итераций не удается найти новое решение. Или другими словами, если на протяжении заданного количества поколений не появляются более удачные особи.
• Threshold — критерий останова, согласно которому генетический алгоритм прерывается, если значение целевой функции лучшего на данный момент решения стало меньше заданного порогового значения.
• CompositeAll — критерий останова, который создается на основе других критериев останова (его конструктор принимает вектор типажей-объектов StopChecker). Этот критерий останавливает генетический алгоритм, если все переданные ему типажи-объекты считают, что генетический алгоритм можно останавливать.
• CompositeAny — критерий останова, который создается на основе других критериев останова (его конструктор принимает вектор типажей-объектов StopChecker). Этот критерий останавливает генетический алгоритм, если хотя бы один переданный ему типаж-объект считает, что генетический алгоритм можно останавливать.

Типаж Logger — лог работы алгоритма

Типаж Logger не влияет на работу генетического алгоритма, но позволяет следить за его работой, а также с помощью этого типажа можно организовать сбор статистики, связанной с работой алгоритма. Типаж Logger описан следующим образом:

pub trait Logger<T: Clone> {
    /// Метод вызывается после создания начальной популяции
    fn start(&mut self, _population: &Population<T>) {}

    /// Метод вызывается перед запуском алгоритма,
    /// в том числе после остановки алгоритма и последующего продолжения расчета
    fn resume(&mut self, _population: &Population<T>) {}

    /// Метод вызывается в конце каждой итерации генетического алгоритма
    /// (после выполнения этапа отбора особей)
    fn next_iteration(&mut self, _population: &Population<T>) {}

    /// Метод вызывается после завершения алгоритма
    fn finish(&mut self, _population: &Population<T>) {}
}

В модуле optlib::genetic::logging содержатся следующие структуры, реализующие типаж Logger:

• StdoutResultOnlyLogger — после завершения работы алгоритма выводит в консоль результат работы;
• VerboseStdoutLogger — в конце каждой итерации выводит в консоль лучшее на данной итерации решение и значение целевой функции для него.
• TimeStdoutLogger — в конце выполнения алгоритма выводит в консоль время, которое занял расчет.

Конструктор структуры GeneticOptimizer в качестве последнего аргумента принимает вектор типажей-объектов Logger, что позволяет гибко настраивать вывод программы.

Функции для тестирования алгоритмов оптимизации

Функция Швефеля

Для тестирования алгоритмов оптимизации было придумано достаточно много функций со множеством локальных экстремумов. Модуль optlib::testfunctions содержит несколько функций, на которых можно тестировать алгоритмы. На момент написания этой статьи в модуле optlib::testfunctions содержится всего две функции.

Одна из этих функций — функция Швефеля, о которой писалось в самом начале статьи. Еще раз напомню, что эта функция записывается следующим образом:

$$

Функция Швефеля имеет один глобальный минимум в точке x' = (420.9687, 420.9687, ...). Значение функции в этой точке равно нулю.

В модуле optlib::testfunctions эта функция называется schwefel. Эта функция принимает вектор из N значений.

Многомерный параболоид

Другая функция для тестирования намного более простая, она имеет всего один экстремум, и для ее оптимизации достаточно простого градиентного спуска, однако эта функция полезна для отладки алгоритмов оптимизации, чтобы выявить проблемы на простой функции.

Эта функция записывается следующим образом:

$$

Эта функция принимает минимальное значение в точке x' = (1.0, 2.0,… N). Значение функции в этой точке равно нулю.

В модуле optlib::testfunctions эта функция называется paraboloid.

Заключение

Описанная выше библиотека optlib позволяет создавать различные алгоритмы оптимизации, которые можно динамически выбирать в процессе выполнения программы. На момент написания этой статьи в этой библиотеке реализован только генетический алгоритм (модуль optlib::genetic), однако в будущем планируется добавить и другие алгоритмы глобальной оптимизации, такие как алгоритм роя частиц, алгоритм роя пчел, алгоритм имитации отжига и др.

Многое еще можно улучшать в модуле optlib::genetic. Помимо добавления новых алгоритмов для различных этапов работы генетического алгоритма для ускорения расчета можно использовать параллельные вычисления. Также планируется добавить новые логгеры для вывода результатов не в консоль, а в файлы, а также структуру для сбора статистики процесса работы алгоритма, чтобы можно было построить график сходимости генетического алгоритма, узнать сколько раз вызывался расчет целевой функции.

В качестве отдельного примера может быть полезна программа, которая запускает генетический алгоритм множество раз и сохраняет усредненную статистику. Хотелось бы сделать программу с графическим интерфейсом, которая бы выводила статистику выполнения алгоритма в процессе работы (график сходимости, распределение особей по пространству поиска и т.д.)

Помимо этого планируется добавить новые аналитические функции (помимо функции Швефеля) для тестирования алгоритмов оптимизации.

Еще раз напомню ссылки, связанные с библиотекой optlib:

• Страница на github — https://github.com/Jenyay/rust-optimization
• Страница на crates.io — https://crates.io/crates/optlib
• Документация — https://docs.rs/optlib

Жду ваших комментариев, дополнений и замечаний.