Несколько слов о «золотом сечении» в традиционном смысле
Считается, что если отрезок разделить на части таким образом, что меньшая его часть будет относиться к большей, как бОльшая – к целому отрезку, то такое разделение дает пропорцию 1/1,618, которую древние греки, позаимствовав ее у еще более древних египтян, назвали «золотым сечением». И что многие архитектурные сооружения – соотношения контуров строений, соотношение между их ключевыми элементами — начиная с египетских пирамид и кончая теоретическими построениями Ле Корбюзье — основывались на этой пропорции.
Ей же соответствуют числа Фибоначчи, спираль которого дает развернутую геометрическую иллюстрацию этой пропорции.
Более того, размеры человеческого тела (от подошв до пупка, от пупка до головы, от головы до пальцев поднятой руки), начиная от идеальных пропорций, увиденных в Средневековье (витрувианский человек и проч.), и кончая антропометрическими измерения населения СССР, довольно-таки близки к этой пропорции.
А если добавить, что подобные фигуры обнаружены в совершенно разнородных биологических объектах: раковинах моллюсков, расположении семян в подсолнухе и в кедровых шишках, то понятно почему иррациональное число, начинающееся как 1,618 объявлялось «божественным» — его следы прослеживаются даже в форме галактик, тяготеющих к спирали Фибоначчи!
С учетом всех перечисленных примеров, можно предполагать:
- мы имеем дело с поистине «большими данными»,
- даже в первом приближении они указывают на некую, если не всеобщность, то необыкновенно широкое распространение «золотого сечения» и близких к нему значений.
В экономике
Широко известны и интенсивно используется диаграммы Лоренца для визуализации доходов населения. Эти мощный макроэкономический инструмент с разнообразными вариациями и уточнениями (децильный коэффициент, индекс Джини) используются в статистике для социально-экономического сопоставления стран и их особенностей и могут быть обоснованием для принятия больших политических и бюджетных решений в области налогообложения, здравоохранения, выработки планов развития стран и регионов.
И хотя в нормальном бытовом сознании доходы и расходы связаны между собой накрепко, в Гугле это не так… Поразительно, но найти связь диаграмм Лоренца с распределением расходов мне удалось только у двух российских авторов (буду признателен, если кто-то знает подобные работы как в русском, так и англоязычном секторе интернета).
Первая — диссертация Т. М. Буевой. Диссертация была посвящена, в частности, оптимизации расходов на марийских птицефабриках.
Другой автор, В.В. Матохин (взаимные ссылки авторов имеются), подходит к делу более масштабно. Матохин, физик по исходному образованию, занимается статистической обработкой данных, используемых при принятии управленческих решений, а также оценкой адаптивности и управляемости компаний.
Концепция и примеры, приводимые ниже, почерпнуты из работ В. Матохина и его коллег (Матохин, 1995), (Antoniou и др., 2002), (Крянев, и др., 1998), (Матохин и др. 2018). В связи с этим следует добавить, что возможные ошибки в интерпретации их работ являются исключительной собственностью автора этих строк и не могут быть приписаны исходным академическим текстам.
Неожиданное постоянство
Отраженное на ниже представленных графиках.
1. Распределение грантов по конкурсу научно-технических работ по Государственной программе “Высокотемпературная сверхпроводимость”. (Матохин, 1995)
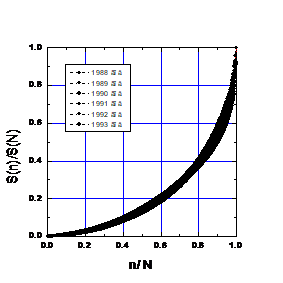
Рис.1. Пропорции в ежегодном распределении средств по проектам в 1988-1994 гг..
Основные характеристики ежегодных распределений приведены в Табл.3, где SN — ежегодная сумма распределяемых средств (в млн. руб.), а N — число финансируемых проектов. С учетом того, что за эти годы менялся персональный состав жюри конкурса, бюджет конкурса и даже масштаб денег (до реформы 1991-го года и после), стабильность реальных кривых во времени поразительна. Черная полоса на графике составлена из экспериментальных точек.
| 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | ||
| S | 273 | 362 | 432 | 553 | 345 | 353 | 253 | X |
| Sn | 143.1 | 137.6 | 136.9 | 411.2 | 109.4 | 920 | 977 | Y |
Табл.3
2. Кривая расходов, связанных с продажами товарных запасов (Котляр, 1989)

Рис.2
3. Тарифная сетка жалований чинам
В качестве примера для построения диаграммы взяты данные из документа «Ведомость: сколько каким чинам по штатам обыкновенного годового жалования в год иметь положено» (Суворов, 2014)(«Наука побеждать»).
|
 Рис. 3. Диаграмма соразмерности годовых жалований по чинам |
4. Осредненный рабочий график американского менеджера среднего звена (Mintzberg, 1973)

Рис.4
Приведенные нормированные графики позволяют предполагать, что в иллюстрируемых ими хозяйственных активностях имеется общая закономерность. При радикальном различии по конкретике хозяйственной деятельности, по ее месту и времени, весьма вероятно, что сходство графиков продиктовано неким фундаментальным условием функционирования экономических систем. Не иначе, как за тысячелетия ведения хозяйственной деятельности на основании огромного числа проб и ошибок субъекты этой деятельности нащупали некоторую оптимальную стратегию распределения ресурсов. И интуитивно используют ее в текущей деятельности. Такое предположение хорошо согласуется с известным принципом Парето: 20% наших усилий дают 80% результатов. Здесь явно наблюдается нечто подобное. Приведенные графики выражают эмпирическую закономерность, которая в случае преобразования в диаграмму Лоренца с достаточной точностью описывается при показателе степени «альфа» равном 2. При этом показателе диаграмма Лоренца превращается в часть окружности.
Можно назвать эту, еще не имеющую устойчивого наименования характеристику, выживаемостью. По аналогии с выживаемостью в дикой природе, выживаемость хозяйственной системы определяется ее наработанным приспособлением к условиям социально-экономической среды и способностью адаптироваться к изменениям рыночных условий.
Это значит, что система, в которой распределение расходов близко к идеальному (при показателе степени «альфа», равном 2, или распределением расходов «по окружности»), имеет наибольшие шансы сохраниться в существующем виде. Примечательно, что в ряде случаев такое распределение определяет и наибольшую рентабельность предприятия. Например, здесь. Чем меньше коэффициент отклонения от идеального, тем выше рентабельность предприятия (Буева, 2002).
Таблица (фрагмент)
| Наименование хозяйства, района | Рентабель-ность (%) | Коэффициент отклонения | |
| 1 | ГУП п/ф «Волжская» Волжского р-она | 13,0 | 0,336 |
| 2 | СПК п/ф «Горномарийская» | 11,1 | 0,18 |
| 3 | УМСП с-з «Звениговский» | 33,7 | 0,068 |
| 4 | ЗАО «Марийское» Медведевского р-на | 7,5 | 0,195 |
| 5 | ОАО «Тепличное» Медведевского р-на | 16,3 | 0,107 |
| ... | |||
| 47 | СПК (к-з) «Рассвет» Советского р-она | 3,2 | 0,303 |
| 48 | С-з «Броневик» Килемарского р-она | 14,2 | 0,117 |
| 49 | СПК СХА «Авангард» Моркинского р-она | 6,5 | 0,261 |
| 50 | СХА к-з им. Петрова Моркинского р-она | 22,5 | 0,135 |
Практические выводы
Планируя расходы, как компании, так и домохозяйства, полезно построить по ним кривую Лоренца и сверить ее с идеальной. Чем ближе ваша диаграмма будет к идеальной, тем вероятнее, что планируете правильно и что ваша деятельность будет успешна. Такая близость подтверждает, что ваши планы близки к опыту хозяйственной деятельности человечества, отложившемся в таких общепризнанным эмпирических закономерностях, как принцип Парето.
Однако можно предположить, что здесь речь идет о функционировании зрелой хозяйственной системы, ориентированной на рентабельность. Если же речь не идет о максимизации прибыли, а, например, о задаче модернизации компании или о принципиальном увеличении ее доли рынка, ваша кривая распределения расходов будет отходить от окружности.
Понятно, что и в случае старт-апа с его специфической экономикой диаграмма Лоренца, отвечающая наибольшей вероятности успеха, будет также отклоняться от окружности. Можно высказать гипотезу, что отклонения кривой распределения расходов внутрь окружности соответствует как повышенным рискам, так и пониженной адаптивности компании. Однако без опоры на большие статистические массивы по старт-апам (как успешным, так и неуспешным) обоснованные квалифицированные прогнозы вряд ли возможны.
По другой гипотезе, отклонение кривой распределения расходов от окружности наружу, может быть сигналом как чрезмерной зарегулированности управления, так и сигналом надвигающегося банкротства. Для проверки этой гипотезы так же необходима определенная эталонная база, которая, как и в случае старт-апов, вряд ли существует в открытом доступе.
Вместо заключения
Первые большие публикации по этой тематике датируются 1995 годом (Матохин, 1995). И малоизвестность этих работ при их универсальности и радикально новом использовании широко применяемых экономистами моделей и инструментов остается в некотором смысле загадкой…
Комментарии (15)

Yuri2110 Автор
17.08.2019 09:38Инфляция денег во многом зависит от времени и места, и какие-либо отчетливые закономерности здесь не просматриваются (кроме общего инфляционного тренда). Например, в случае доллара (одной из самых устойчивых валют), так он «легчал» с 1913 по 2018 год на 1,8% в год.
fxtop.com/ru/inflation-calculator.php

ybqwer
17.08.2019 09:57может это просто кривая инфляции денег, нет?

Yuri2110 Автор
17.08.2019 10:01Инфляция денег во многом зависит от времени и места, и какие-либо отчетливые закономерности здесь не просматриваются (кроме общего инфляционного тренда). Например, в случае доллара (одной из самых устойчивых валют), так с 1913 по 2018 год он «легчал» на 1,8% в год.
fxtop.com/ru/inflation-calculator.php

S_A
17.08.2019 10:25Есть торговая стратегия "золотое сечение" на финаме, в топе кстати. Числа Фибоначчи часто используются в техническом анализе в торговле на бирже.
Золотое сечение и спираль это просто фазовая траектория некоторого дифура, неплохо описывающего механику упорядочения в системах с определённого рода постоянным внешним воздействием.

Yuri2110 Автор
17.08.2019 11:18Вопрос поставлен серьезно, и боюсь, выходит за рамки моей компетентности как интерпретатора.
Могу сказать только, что числа Фибоначчи формируются по известному правилу, а в данном случае правило формирования системы платежей неизвестно.
И что вопрос о фазовых траекториях экономической системы прорабатывается. В качестве первого шага выведена плотность распределения вероятности значений долей платежей. Это здесь: Крянев А. В., Матохин В. В. и Климанов С. Г. Статистические функции распределения ресурсов в экономике [Отчет]. — М: Препринт МИФИ, 1998). Если буду располагать релевантной информацией, отвечу дополнительно.

AC130
17.08.2019 20:10А можно к каждому графику пояснение, что именно по oX, oY, и как именно из табличных данных были получены точки на графике? И каким образом связана окружность (из легенды) и золотое сечение?

Yuri2110 Автор
17.08.2019 21:54Диаграмма Лоренца для произвольного ряда чисел {G} на конкретном примере. В качестве исходного ряда берем произвольный ряд чисел: 600, 70, 100, 200, 30. Упорядочим выбранный ряд чисел по их величине: 30; 70; 100; 200; 600 и рассчитаем ряд накопленных сумм {S} по формуле:
Sn = G1 + … + Gn,
где n=1, 2, …, N.
Значения, откладываемые по оси «Y», определяются нормированием накопленных сумм на сумму всех чисел Yn = Sn/SN. Соответствующие значения координат по оси «X», определяются как Xn = n/N.
В итоге, откладывая полученные точки внутри квадрата со сторонами равными единице (или 100%), получаем диаграмму соразмерности исследуемого ряда.
На второй вопрос отвечу завтра.

Yuri2110 Автор
18.08.2019 11:13Пояснения к вопросу о построениии графика тут
tekora.ru/press_centr/publikacii/sorazmernost-i-rentabelnost-zatrat/?PAGEN_2=2#_Toc525139399
О связи окружности и золотого сечения. Строгого математического соотвествия нет. Однако на основании больших объемов эмпирического материала окружность рассматривается как удобная аппроксимирующая функция соразмерности. Подтверждением допустимости этого служат выше приводимые графики, связанные с разнообразными хозяйственными активностями. В упомянутой диссертации Т. М. Буевой, в частности, критерий оценки полученных кривых Лоренца (довольно сложная функция) может быть сравнен с пропорцией золотого сечения (1,618033). Это сравнение дает несовпадение критерия всего на 0,5%.
А первые шаги по построению теоретических количественных моделей здесь
tekora.ru/press_centr/publikacii/sorazmernost-i-rentabelnost-zatrat/?PAGEN_2=3&ELEMENT_CODE=sorazmernost-i-rentabelnost-zatrat#nav_start_2


SemenPV
Рен-ТВ?
BlackMokona
http://hiblogger.net/img/articles_img/4/f/0/111111111111-u12nq.jpg
Yuri2110 Автор
Исследование необходимо продолжить! :)
Yuri2110 Автор
Не совсем понятен вопрос. Если сомнения возникают по поводу «золотого сечения» в природе и искусстве, то одно из самых коротких видео по теме www.youtube.com/watch?v=uzoHfXjvAV8. Если по поводу распределения расходов, то, в частности, статья
Analysis of resources distribution in economics based on entropy I. Antonioua I.; V.V. Ivanova; Yu.L. Korolev; A.V. Kryaneva; V.V. Matokhin; Z. Suchaneckia в таком серьезном журнале как Physica A. (- 2002 г… — Т. 304. — стр. 525-534). И здесь: Матохин В. В. Соразмерность и рентабельность затрат. — ТЕКОРА, 2018 г… — tekora.ru/press_centr/publikacii/sorazmernost-i-rentabelnost-zatrat.
SemenPV
Сомнения по поводу «золотого сечения» в природе и искусстве не возникают. Возникает сомнение в качестве аргументации для
вы бы лучше совсем никаких данных не приводили, чем откровенно высосанные из пальца.Загадки нету, если его работа базируется на примерно такого-же качества данных. Поэтому и выглядит как передача на РенТВ.Уж в чём-чём, а в экономике на затраты для исследований не скупятся.
Yuri2110 Автор
Если эти данные представняются неубедительными, возьмите свою кредитку и проверьте соотношение ее сторон.
И увидите прямую связь экономики и «золотого сечения»!
SemenPV