Привет, Хабр!

В колористике существует несколько методов построения цветовой гаммы (цветовой палитры), основанных на расположении цветов друг относительно друга в цветовом круге и, как правило, имеющих одинаковую яркость. Гармоничность восприятия которых не обоснована в достаточной степени с физической точки зрения.

В теории музыки есть понятие консонирующих интервалов. Консонансами называют интервалы, звучащие более мягко и гармонично. Есть три группы консонансов: весьма совершенные (чистый унисон, октава), совершенные (чистая квинта, чистая кварта) и несовершенные (большая терция, малая терция, секста). Также есть понятие консонирующего аккорда — мажорное или минорное трезвучие, состоящее исключительно из консонирующих интервалов.

Акустически сущность разницы между консонансом и диссонансом выражается в различной длине периодов регулярно повторяющихся групп колебаний. Критерием различия между консонансом и диссонансом является простота или сложность отношений: чем проще отношения, тем консонантнее, чем сложнее — тем диссонантнее, где числовые пропорции можно выражать двояко: через отношения длин струн либо через отношения числа колебаний. Другими словами, степень консонантности двух нот определяется числом совпадений периодов соответствующих гармонических функций зависимости звукового давления от времени за единицу времени.

Рис. 1: График зависимости звукового давления от времени на фиксированном расстоянии от источника звука.

К примеру, ноты до и соль (чистая квинта) имеют длины звуковых волн отличающиеся в полтора раза. Графики функций зависимости звукового давления нот от времени пересекаются на оси абсцисс (звуковое давление равное нулю) когда функция звукового давления ноты до делает два колебания, а функция ноты соль — три (рис. 1). На рисунке 1 этот момент отмечен вертикальной чертой.

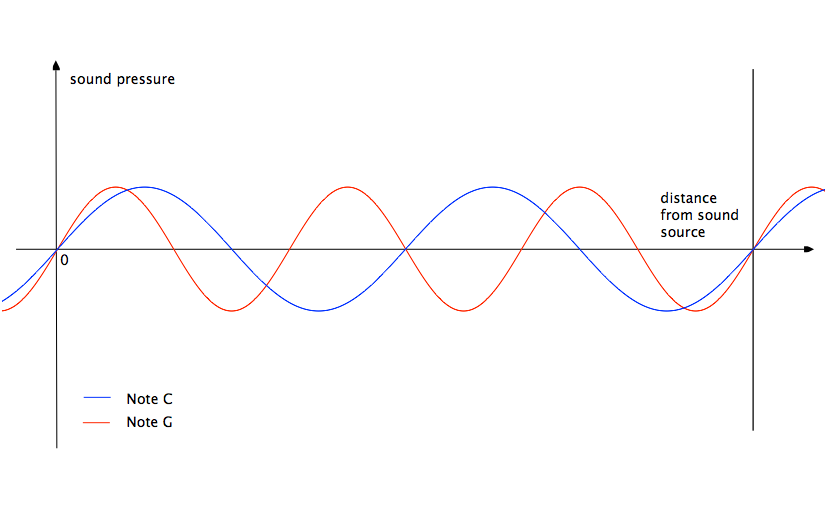
Рис. 2: График зависимости звукового давления от расстояния от источника в фиксированный момент времени.

Если представить распространение звукового давления в пространстве в фиксированный момент времени (вблизи источника звука), то мы получим такой же рисунок (рис. 2).

Ноты до и ми (большая терция) имеют длины звуковых волн отличающиеся в 5/4 раза. Их графики пересекаются на оси абсцисс когда функция звукового давления ноты до делает 4 колебания, а функция ноты ми — 5. Именно по-этому чистая квинта является более консонантной чем большая терция.

Цвет, как и звук, является также и волной (корпускулярно-волновой дуализм). В случае построения консонирующего интервала для цвета мы не ограничены небольшим набором нот, но ограничены границами длин волн видимого света, также как и звук ограничен границами длин волн слышимого звука. Отсутствие ограничения небольшим набором нот приводит к тому, что мы можем значительно расширить список интервалов — 3/2; 3/4; 2/5, 3/5, 4/5,...

Волновой метод построения цветовой гаммы

Рассмотрим построение цветовой гаммы для спектральных и неспектральных цветов.

Спектральный цвет представляет собой цвет, имеющий определенную длину волны. Для построения цветовой палитры возьмем, сначала, наиболее консонантный к нему цвет — это цвет с длиной волны, отличающейся в 1,5 раза, но не выходящий за пределы видимого спектра. Далее, аналогичным образом, будем брать менее консонантные интервалы до тех пор, пока не достигнем желаемого количества цветов в искомой палитре.

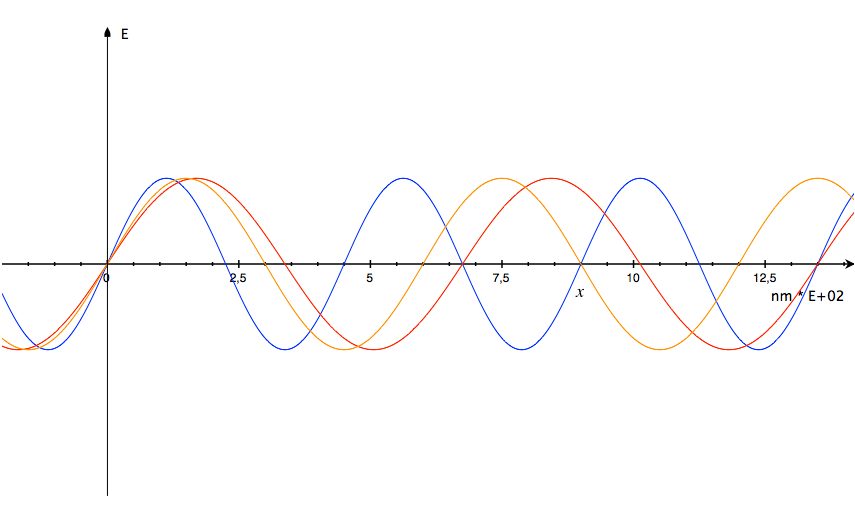
Рис. 3: График зависимости напряженности электрического поля от расстояния от источника в фиксированный момент времени.

Возьмем, например, синий цвет с длиной волны 450 нм. Цвет, длина волны которого меньше в 1,5 раза, выходит за рамки видимого излучения. Цвет с длиной волны большей в 1,5 раза (675 нм.) — это красный цвет. Цвет с длиной волны большей в 3/4 раза (600 нм.) — это оранжевый цвет. В итоге мы получили следующую цветовую гамму: основной цвет — синий, наиболее подходящий к нему цвет — красный, немного менее подходящий к синему цвету — оранжевый цвет (рис. 3). К тем же результатам можно прийти оперируя вместо длин волн их частотами.

Также в музыке существует понятие лада. Сочетание нот может звучать не только гармонично, но и иметь оттенок — лад (ионийский, дорийский, фригийский, лидийский, ...). Аналогичные ощущения можно перенести и в цветовую гамму, используя при ее построении соответствующие пропорции.

К неспектральным цветам относят цвета которые не содержатся в спектре и состоят из нескольких спектральных цветов. Исходя из закона аддитивности Грассмана следует, что в случае подбора цветовой гаммы для неспектральных цветов следует производить те же операции над его составляющими цветами сохраняя пропорции и учитывая границы длин волн видимого спектра.

Рассмотрим подрбонее явление консонанса между двумя неспектральными цветами. Музыкальный звук состоит из элементарных тонов так как вместе с колебанием самого источника звука в целом, одновременно колеблются и его части. Колебания частей вибрирующего тела рождают слабые призвуки — обертоны, поглощаемые основным тоном. Образующая сложный звук шкала простых тонов соответствующих амплитуд называется частотным спектром. Все элементарные тоны входящие в сложный звук называются гармониками. Степень консонантности интервала определяется числом совпадающих гармоник спектров обоих нот: чем большее число гармоник совпадает, тем консонантнее интервал.

Рис. 4: График зависимости звукового давления от времени на фиксированном расстоянии от источника звука.

Исходя из этого мы полагаем что суть явления гармонии (консонанса) состоит в одновременном состоянии покоя (энергия равна нулю) обеих волн. На графиках это состояние покоя отображается в пересечении двух волновых функций на оси абсцисс (времени) (рис. 4). И степень консонантности двух волновых функций определяется количеством таких пересечений за единицу времени (либо длины, при условии одинаковой скорости распространения): чем больше — тем консонантнее. Данное понятие степени консонантности распространяется также и на неспектральные цвета, так как они также являются волновыми функциями.

Реализация волнового метода на примере белого цвета в системе sRGB

Человек способен воспринимать цвета с длинами волн в диапазоне 380 — 780 нм. Любые четыре цвета являются линейно зависимыми, однако существует бесконечное количество комбинаций из трех цветов, которые являются линейно независимыми (первый закон Грассмана). Независимость цветов по Грассману состоит в том, что цветовое ощущение, вызываемое одним из тройки цветов, не может быть получено путем смешивания двух других цветов в каких-либо пропорциях. Было замечено, что наиболее удобно оперировать красным, зеленым и синим цветами. Именно по такому принципу и работают почти все современные мониторы.

В 1931 году Международным Осветительным Конгрессом (CIE) была принята характеристика цветовых свойств среднего (стандартного) наблюдателя, основанная на результатах полученных в 1926 — 1930 гг. Райтом и Гилдом. В основу данного колориметрического стандарта, действующего по сей день, легли следующие цвета: 700 нм. (красный), 546.1 нм (зеленый) и 435.8 нм. (синий) (система RGB). Принятая характеристика содержит взаимосвязь между результирующей длиной волны смеси и количеством красного, зеленого и синего цветов в данной смеси.

В дальнейшем, для удобства вычислений, Международный Осветительный Конгресс ввел абстрактную систему CIE XYZ, основанную на нереальных цветах. Данная координатная система очень удобна для осуществления перехода от одной системы к другой. Также были рассчитаны длины волн видимого света и соответствующие координаты CIE XYZ смеси, основываясь на результатах полученных для системы RGB.

Для воспроизведения одинаковых цветовых ощущений на различных устройствах вывода (монитор или принтер) каждое такое устройство имеет свой цветовой профиль, который содержит его связь с абстрактной системой CIE XYZ. Другими словами, цветовой профиль служит для возможности перехода между различными цветовыми системами (sRGB, AdobeRGB, ...). Наиболее распространенным цветовым пространством является система sRGB. Далее рассмотрим реализацию волнового метода именно для этой системы.

Найдем длины волн красного, зеленого и синего цвета в системе sRGB. Для этого воспользуемся формулами перехода из системы sRGB в CIE XYZ (с точкой белого D65). В результате для красного rgb(255, 0, 0), зеленого rgb(0, 255, 0) и синего rgb(0, 0, 255) получим следующие координаты в системе CIE XYZ: красный — (0.412456, 0.212673, 0.019334), зеленый — (0.357576, 0.715152, 0.119192), синий — (0.180437, 0.072175, 0.950304).

Используя таблицы содержащие длины волн видимого света (CIE 1931 2-deg, XYZ CMFs) и соответствующие координаты CIE XYZ смеси, найдем длины волн для красного, зеленого и синего цветов в системе sRGB: красный — 611.4 нм., зеленый — 549.1 нм., синий — 464.2 нм.

Теперь найдем "чистую квинту" для данного цвета — цвет с длиной волны большей в 1,5 раза:
для красного — 611.4 нм. x 1.5 = 917,1 нм. (выходит за рамки видимого спектра, черный цвет),
для зеленого — 549.1 нм. x 1.5 = 823,65 нм. (практически черный цвет),
для синего — 464.2 нм. x 1.5 = 696,3 нм. (красный цвет).

Далее, используя те же таблицы, найдем координаты для полученных волн в системе CIE XYZ:
для красного — 917,1 нм. — (0, 0, 0),
для зеленого — 823,65 нм. — (0.000001905497, 0.000000688110, 0.000000000000),
для синего — 696,3 нм. — (0.014790640000, 0.005343059000, 0.000000000000).

Затем переведем каждый из полученных цветов обратно в систему sRGB:
для красного — 917,1 нм. — rgb(0, 0, 0),
для зеленого — 823,65 нм. — rgb(0.0168, -0.0018, 0.0000),
для синего — 696,3 нм. — rgb(56.1246, -13.7888, -0.8801).

Округлив до целых и отбросив то что меньше нуля, получим:
для красного — 917,1 нм. — rgb(0, 0, 0),
для зеленого — 823,65 нм. — rgb(0, 0, 0),
для синего — 696,3 нм. — rgb(56, 0, 0).

Рис. 5: Изображение цвета rgb(56, 0, 0).

Просуммировав три получившихся цвета получим в итоге темно-красный цвет который в спектре близок к инфракрасному — rgb(56, 0, 0) (рис. 5).

Выше была показана реализация алгоритма на примере белого цвета rgb(255, 255, 255) умноженного на 3/2. Здесь не была учтена относительная яркость, для вычисления которой необходимо также производить преобразование в систему xyY.

Реализация волнового метода в компьютерной графике

На ряду с системами sRGB и CIE XYZ существует также система xyY, где компоненты x и y отвечают за длину волны, а компонент Y — за относительную яркость цвета. Произведем преобразование из предыдущего пункта с произвольным цветов rgb(r, g, b). Для этого найдем сначала координаты максимальных красного, зеленого и синего цветов в системе xyY:
rgb(255, 0, 0) — xyY(0.640000, 0.330000, 0.212673),
rgb(0, 255, 0) — xyY(0.300000, 0.600000, 0.715152),
rgb(0, 0, 255) — xyY(0.150000, 0.060000, 0.072175).

В данном случае нас интересует только составляющая яркости Y:
rYmax = 0.212673,
gYmax = 0.715152,
bYmax = 0.072175.

Далее переведем синий цвет rgb(0, 0, b) в систему xyY, через CIE XYZ с учетом гамма-коррекции:
rgb(0, 0, b) — xyY(bx, by, bY).

В результате яркость того цвета, который мы получали для синего в предыдущем пункте, должна быть меньше в bY/bYmax раза. Для цвета rgb(0, 0, 255) мы получали цвет с длиной волны 696,3 нм. что соответствует цвету в системе xyY с координатами xyY(0.734621, 0.265379, 0.00543824). В итоге получим: xyY(0.734621, 0.265379, 0.00543824 * bY/bYmax). Далее выполним преобразование в систему sRGB и получим цвет rgb(br, bg, bb).

Выполняя аналогичные действия для цветов rgb(r, 0, 0) и rgb(0, g, 0) получим rgb(rr, rg, rb) и rgb(gr, gg, gb) соответственно.

Далее сложим эти цвета с учетом яркости. Просуммируем сначала rgb(rr, 0, 0), rgb(gr, 0, 0) и rgb(br, 0, 0). Путем перевода каждого из этих цветов в систему xyY получим соответствующие яркости — rrY, grY, brY. Найдем суммарную яркость красного: rY = rrY + grY + brY. Итоговый цвет будет иметь следующие координаты — xyY(0.640000, 0.330000, rY). При переводе в систему sRGB получим rgb(rNew, 0, 0). Аналогичным образом найдем gNew и bNew. Итоговый цвет в системе sRGB будет иметь координаты rgb(rNew, gNew, bNew).

P. S.

В данной статье был описан и обоснован с физической точки зрения разработанный нами волновой метод построения цветовой гаммы. Было описано свое понимание сути явления гармонии. Также в статье был описан алгоритм реализация волнового метода для цветовой модели sRGB в компьютерной графике.

Данный метод может найти широкое применение в различных отраслях дизайна. Результаты работы находятся на сайте https://wavepalette.com/ru/ и будут регулярно дополняться и, при необходимости, корректироваться. Соответствующая статья была опубликована на сайте arxiv.org.

P. P. S.

На сайте рядом с каждым цветом преобразование и направление обозначено дробью и стрелкой (3/2^). Двойное преобразование обозначено двумя стрелками (4/3^^ что равносильно 16/9^). Первые два цвета почти всегда будут темно-красным и темно-фиолетовым, так как преобразование 3/2 и 2/3 близки к инфракрасному и ультрафиолетовому цвету спектра. Сначала я думал исключить их из палитры, но потом решил все-таки оставить.

P. P. P. S.

Алгоритм построения цветов для любого цвета в системе sRGB пока еще требует доработки. Хорошие результаты, на мой взгляд, которые можно использовать алгоритм показывает на спектральных цветах — https://wavepalette.com/ru/spectral/.