Существует ли объективная, идеальная случайность, или она является следствием нашего неведения?

Жизнь – штука непредсказуемая, и случайности происходят с нами постоянно. Можно сказать, что сама по себе Вселенная случайно. И, тем не менее, каким-то образом большие количества случайных событий могут создавать крупномасштабные закономерности, которые наука способна предсказывать. Рассеяние тепла и броуновское движение – всего лишь два примера таких событий.

Недавно случайность даже попала в новостные ленты: оказалось, что у случайных поверхностей имеется скрытый порядок, а ещё мы, возможно, близко подошли к тому, чтобы увидеть, как квантовый компьютер генерирует идеальную случайность. Последний случай, поиски идеальной случайности, важен потому, что случайность приносит непредсказуемость, и у всех не относящихся к квантовым технологиям попыток достичь её есть один скрытый недостаток: они реализованы посредством алгоритмов, которые, теоретически, можно расшифровать. В данной колонке мы изучим, как можно создать случайность и победить её в повседневной жизни, перед тем, как подниматься на философские вершины дебатов о том, что есть истинная случайность.

Загадка 1: случайные комбинации

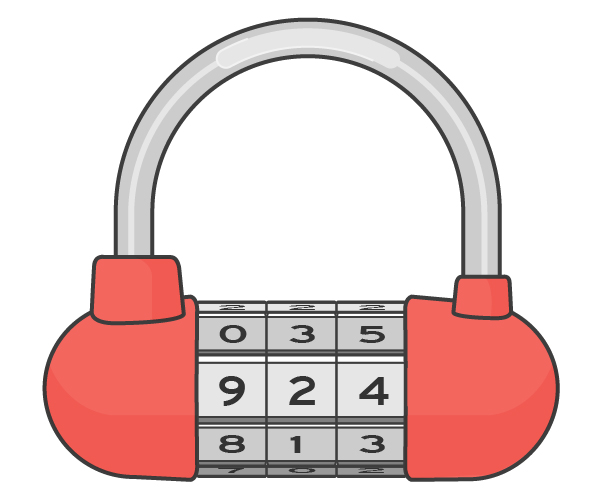
Рассмотрим простой кодовый замок для велосипеда, похожий на приведённое изображение. У него есть три вращающихся диска, на каждом из которых изображено 10 цифр по порядку. Когда три эти диска повёрнуты так, чтобы выдать заданную комбинацию – 924 – замок открывается. Когда вы хотите закрыть его, вам нужно перемешать цифры так, чтобы они далеко отстояли от заданной комбинации. Но что означает «далеко» в данном контексте? Если вы переместите диск максимально, на 5 положений, вы зададите номер 479. Однако взломщику будет легко случайно наткнуться на эту позицию, если он просто повернёт все пять дисков одновременно, и посмотрит, не откроется ли замок. Представьте, что у взломщика есть время на испытание пяти различных комбинаций. В каждом случае наш потенциальный вор пробует наш замок после одного из следующих действий (а в случае неудачи возвращает замок к изначальной конфигурации):

• Повернуть один диск на случайное число позиций.
• Повернуть два диска одновременно на случайное число позиций.
• Повернуть все три диска одновременно на случайное число позиций.
• Повернуть два диска на разные углы.
• Повернуть все три диска по-разному.,

Наша загадка следующая: если код открытия замка – 924, какой набор перемешанных чисел будет наиболее стойким для случайных попыток открыть замок, и сколько таких наборов существует? Какова вероятность обнаружить код?

Загадка 2: от случайности к порядку в загадках

Меня часто удивляет, насколько похож процесс решения загадки на научный прогресс. Мы идём от случайности к порядку, добавляя кусочки, и наша уверенность в правильности решения подпитывается с каждым новым подходящим кусочком. Во второй задаче мы попробуем создать способ измерения нашего прогресса на пути от случайного беспорядочного состояния к законченному, упорядоченному решению.



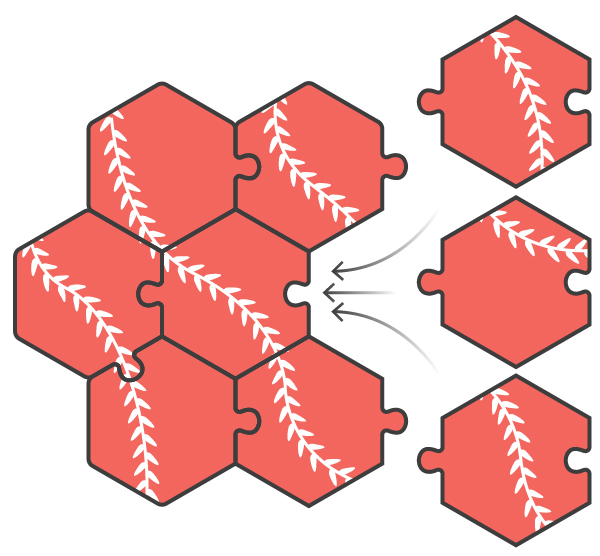
Допустим, мы решаем пазл, состоящий из шестиугольных кусочков – как соты. Картинка пазла представляет собой вьющуюся лиану. Поскольку узор повторяющийся и самоподобный, нельзя гарантировать, что два соседних кусочка подходят друг к другу физически, даже если они подходят по картинке. Допустим, что к каждому краю заданного кусочка могут подойти три других. Поэтому, когда два кусочка подходят к друг другу по картинке, то вероятность того, что они подойдут физически, составит 33,33%. Однако если вы сможете найти ещё один кусочек, подходящий к обоим рассматриваемым, то есть, такой, у которого по одному общему краю с каждым из этих двух, то ваша уверенность в успехе возрастает. Попробуем оценить, насколько именно она возрастает.

1. Вы нашли три кусочка, на первый взгляд подходящих друг к другу, без очевидного смещения рисунка лианы на их соприкасающихся краях. Какова мера вашей уверенности в правильности подбора кусочков?
2. Вы нашли центральный шестиугольный кусочек, и шесть его окружающих, и по картинке они вроде бы совпадают. Какова мера вашей уверенности в правильности подбора кусочков?

Чем больше становятся группы из кусочков, тем сильнее ваша уверенность в правильности их сборки. Разумно предположить, что три изолированных группы, в которых в сумме есть семь соединённых кусочков, по уверенности не сравнимы с единственным окружённым шестиугольником, описанным выше.

Третья часть этой загадки имеет допускает поправки, и является попыткой количественно оценить указанную выше разницу. Можно ли придумать меру степени завершённости частично решённого пазла? Таковой метод должен позволять назначить число от 0 до 100 любому частично собранному пазлу из шестигранников размером 10х10. Это число должно обозначать степень завершённости, грубо коррелирующую с пропорцией текущего состояния пазла по отношению к законченному варианту.

Загадка 3: возможна ли идеальная случайность?

Для этой части я приведу вам вариант знаменитых дебатов Эйнштейна-Бора для случайности. Участники дебатов могут присоединяться к командам Э или Б.

Обе команды соглашаются, что в макромире существование генерирующих случайность механизмов возможно только потому, что мы не понимаем сил, или алгоритмов, лежащих в их основе. Если бы вам были известны все силы, действующие на подброшенную монетку или брошенный кубик, то при наличии достаточных вычислительных мощностей вы могли бы предсказать результат. Нас учат, согласно преобладанию взглядов команды Б, что в квантовом мире это не так – квантовые вероятности должны быть объективными. Но возможно ли это вообще? Не может ли в субквантовом планковском мире существовать некий механизм, решающий, какой из двух равновероятных вариантов будет реализован, даже если у нас никогда не будет возможности изучить этот уровень? Даже если кошмар Эйнштейна с божеством, играющим в кости, реален, должен же у этого божества в голове быть какой-то алгоритм, решающий каждый выбор, вне зависимости от того, насколько он причудливый и нелогичный. Тогда случайность вновь будет обусловлена нашим невежеством. Она будет неизвестна лишь практически, а не случайна объективно.

Стандартный ответ на это от команды Б заключается в том, что квантовый мир просто слишком странный для того, чтобы применять к нему правила, выученные нами на опыте взаимодействия с макромиром. Однако странности бывают двух видов. С одной стороны, странность может заключаться в физической невозможности перемещаться быстрее скорости света. Такая странность может существовать, и она будет означать лишь, что нам нужно пересмотреть наше понимание физического закона в особых обстоятельствах, точно так же, как Эйнштейн пересмотрел закон сложения скоростей Ньютона, который становится неверным при очень больших значениях.

С другой стороны, нечто может быть странным с точки зрения логической невозможности – типа как 2+2 равняется 5. Такой результат невозможен в любой вселенной. Команда Э может утверждать, что идеальная случайность и объективные вероятности логически невозможны. Мы не должны их принимать, а вместо этого должны найти физические механизмы, способные объяснить наблюдаемые результаты, вне зависимости от того, какие существующие законы физики они могут нарушать.

К какой команде присоединитесь вы?

P.S.: Ответы будут опубликованы позже