Есть 364 дня, когда ты можешь получить подарок не на день рождения, и только один – для подарков на день рождения, знаешь ли.
— Льюис Кэрролл

Читатель спрашивает:

Среди моих 1434 фейсбучных френдов сегодня ни у кого нет дня рождения. Каковы шансы такого события, если в году 365,25 дней?

Предположим, что все ваши друзья родились после 1 марта 1900 года.



За последние 114 лет каждые 4 года случался високосный год. Предположив, что все знакомые родились в совершенно случайные дни и года, получим, что есть 4 шанса из 1461, что они родились в любой день, кроме 29 февраля, и 1 шанс из 1461, что они родились 29 февраля.

Давайте посчитаем шансы того, что у произвольного количества ваших друзей сегодня нет дня рождения. Начнём с одного.



Если у вас один друг, и сегодня не 29 февраля, значит шансы того, что у него нет дня рождения, составляют 1457 из 1461, или 99,73%. И это верно для любого из ваших друзей.

Значит, и у второго друга шансы того, что у него нет дня рождения сегодня, составляют 99,73%, и у третьего, и у сотого, и т.д. Для простоты возьмём 6 друзей – какие будут тогда шансы, что ни у кого из них нет сегодня ДР?



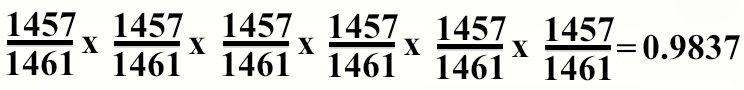
98,37%, поскольку необходимо, чтобы у первого человека не было ДР, и у второго не было, и т.д. Иначе всё пропало.

Забава в том, что эту формулу можно расширить на любое количество людей.

Количество друзей	Шансы для каждого	Общие шансы	В процентах
1 друг	0.99726215	(0.99726215)^1	99.73%
2 друга	0.99726215	(0.99726215)^2	99.45%
5 друзей	0.99726215	(0.99726215)^5	98.64%
10 друзей	0.99726215	(0.99726215)^10	97.30%
50 друзей	0.99726215	(0.99726215)^50	87.19%
150 друзей	0.99726215	(0.99726215)^150	66.28%
253 друга	0.99726215	(0.99726215)^253	49.98%
365 друзей	0.99726215	(0.99726215)^365	36.76%
500 друзей	0.99726215	(0.99726215)^500	25.39%
1000 друзей	0.99726215	(0.99726215)^1000	6.447%
1434 друзей	0.99726215	(0.99726215)^1434	1.961%
1680 друзей	0.99726215	(0.99726215)^1680	0.9993%
2000 друзей	0.99726215	(0.99726215)^2000	0.4156%
2500 друзей	0.99726215	(0.99726215)^2500	0.1055%
3000 друзей	0.99726215	(0.99726215)^3000	0.02679%
5000 друзей	0.99726215	(0.99726215)^5000	0.0001113%

Для небольшого количества друзей шансы велики. Они падают до 50-50 по достижению количества друзей в 253 человека, и после этого быстро уменьшаются. Для 1434 друзей шансы уже менее 2%. Имея 5000 друзей вы получите шансы в 0,0001113%, или 1 к 900000.

А как насчёт более общего подхода? Если мы хотим узнать шансы того, что существует хотя бы один день в году, когда ни у кого нет ДР? Это посложнее.



Если мы посчитаем шансы того, что сегодня ни у кого нет ДР, и вычтем это из 100%, то мы получим шансы того, что у кого-то сегодня есть ДР. Чтобы сложилась ситуация, в которой ни у кого нет ДР, можно вычесть из 100% шансы того, что у кого-то есть ДР в любой из дней года. Это, конечно, будет возможно только при наличии не менее 365 друзей.

Число друзей	Шансы отсутствия ДР	Шансы наличия ДР	Шансы ДР каждый день	Вычтем из 100%
365 друзей	36.76%	63.24%	(0.6324)^365	100% – 2.3 ? 10^-71%
500 друзей	25.39%	74.51%	(0.7451)^365	100% – 2.3 ? 10^-45%
1000 друзей	6.447%	93.553%	(0.93553)^365	99.9999999973%
1434 друзей	1.961%	98.039%	(0.98039)^365	99.927%
1680 друзей	0.9993%	99.0007%	(0.990007)^365	99.927%
2000 друзей	0.4156%	99.5834%	(0.995834)^365	97.44%
2500 друзей	0.1055%	99.8945%	(0.998945)^365	31.97%
3000 друзей	0.02679%	99.97321%	(0.9997321)^365	9.32%
5000 друзей	0.0001113%	99.9998887%	(0.999998887)^365	0.0406%

Получается, что если у вас менее 2000 друзей, почти однозначно в году будет хотя бы один день, когда ни у кого нет ДР, а если более 4000 – то для этого практически не останется шансов.