В прошлой статье мы описали эксперимент по определению минимального объема вручную размеченных срезов для обучения нейронной сети на данных сейсморазведки. Сегодня мы продолжаем эту тему, выбирая наиболее подходящую функцию потерь.
Рассмотрены 2 базовых класса функций – Binary cross entropy и Intersection over Union – в 6-ти вариантах с подбором параметров, а также комбинации функций разных классов. Дополнительно рассмотрена регуляризация функции потерь.
Спойлер: удалось существенно улучшить качество прогноза сети.

Не будем повторять описание специфики проведения сейсморазведки, получаемых данных и задачи их интерпретации. Все это описано в нашей предыдущей статье.
На идею данного исследования нас натолкнули результаты соревнования по поиску солевых отложений на 2D-срезах. По отзывам участников соревнования, при решении этой задачи использовался целый зоопарк различных функций потерь, причем, с разным успехом.
Поэтому мы и задались вопросом – действительно ли для подобных задач на таких данных подбор функции потерь может дать существенный выигрыш в качестве? Или это характерно только для условий соревнования, когда идет борьба за четвертый-пятый знак после запятой для заранее определенной организаторами метрики?
Обычно в задачах, решаемых с помощью нейронных сетей, настройка процесса обучения основывается большей частью на опыте исследователя и некоторых эвристиках. Например, для задач сегментации изображений чаще всего применяются функции потерь, основанные на оценке совпадения форм распознанных зон, так называемые Intersection over Union.
Интуитивно, основываясь на понимании поведения и результатах исследований, такого рода функции дадут лучший результат, чем те, которые не заточены под изображения, как например кросс-энтропийные. Тем не менее, эксперименты в поисках оптимального варианта для такого типа задач в целом и каждой задачи индивидуально продолжаются.
Данные сейсморазведки, подготовленные для интерпретации, обладают рядом особенностей, которые могут оказать существенное влияние на поведение функции потерь. Например, горизонты, разделяющие геологические слои, плавные, более резко изменяющиеся только в местах разломов. Кроме того, выделяемые зоны имеют достаточно большую относительно изображения площадь, т.е. маленькие пятна на результатах интерпретации чаще всего считаются ошибкой распознавания.
В рамках данного эксперимента мы попытались найти ответы на следующие локальные вопросы:
И на более глобальный вопрос:
А стоит ли заморачиваться подбором функции потерь для задач интерпретации сейсмических данных, или полученный выигрыш в качестве не сопоставим с потерями времени на проведение таких исследований? Может, стоит интуитивно выбрать любую функцию и потратить силы на подбор более значимых параметров обучения?
Для эксперимента мы взяли все ту же задачу выделения геологических слоев на 2D-срезах сейсмического куба (см. рисунок 1).
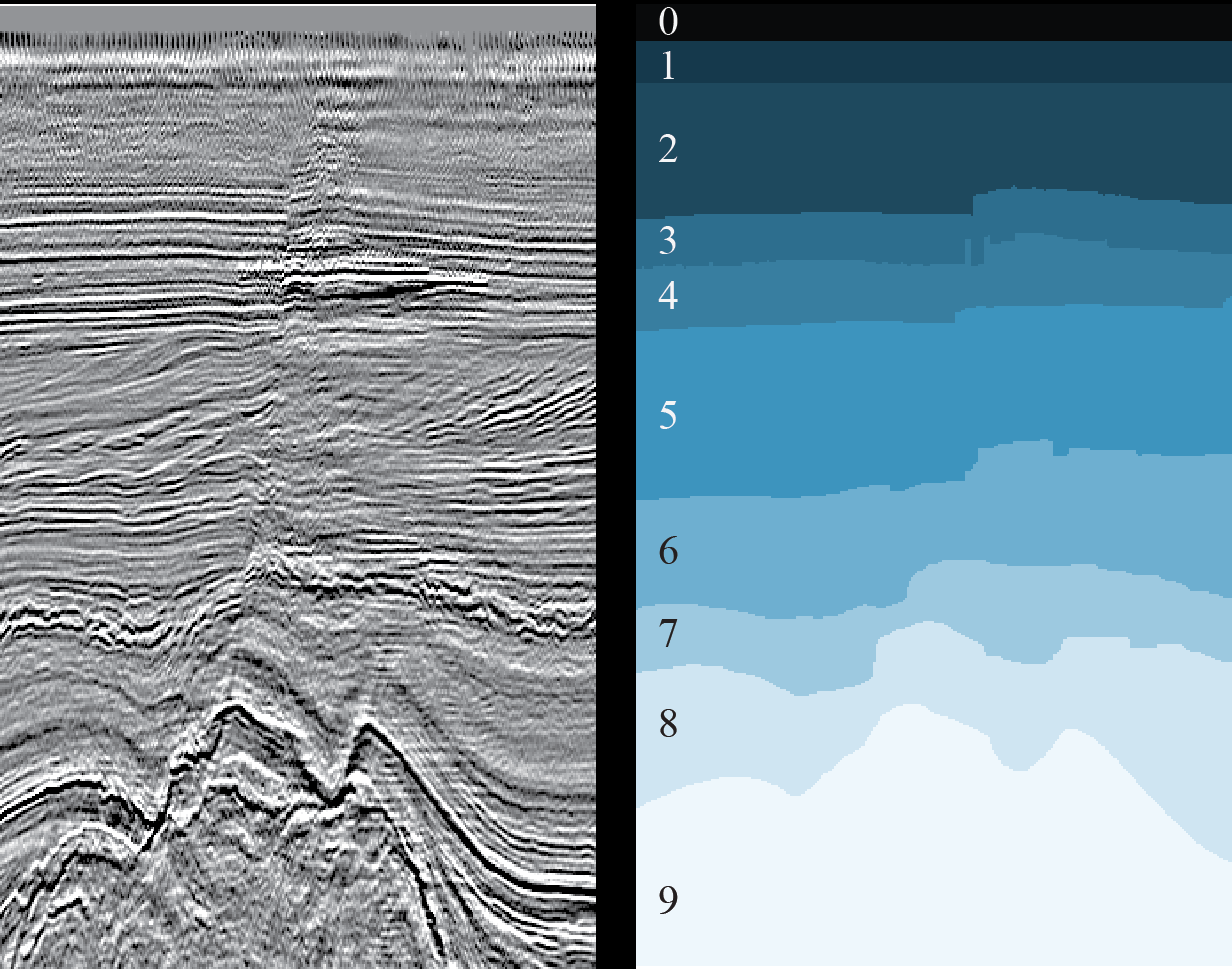
Рисунок 1. Пример 2D-среза (слева) и результата разметки соответствующих ему геологических слоев (справа) (источник)
И тот же набор полностью размеченных данных из голландского сектора акватории Северного моря. Исходные сейсмические данные представлены на сайте Open Seismic Repository: Project Netherlands Offshore F3 Block. Их краткое описание можно найти в статье Silva et al. «Netherlands Dataset: A New Public Dataset for Machine Learning in Seismic Interpretation».
Поскольку в нашем случае речь идет о 2D-срезах, мы использовали не исходный 3D-куб, а уже сделанную «нарезку», доступную здесь: Netherlands F3 Interpretation Dataset.
В процессе эксперимента мы решили следующие задачи:
Для сравнения мы использовали результаты предыдущего эксперимента, в котором функция потерь была выбрана исключительно интуитивно и представляла собой комбинацию функций разных классов с коэффициентами, так же выбранными «на глаз».
Результаты данного эксперимента в виде оценочных метрик и предсказанных сетями масок срезов представлены далее.
В качестве исходных данных мы использовали готовые инлайны и кросслайны сейсмического куба из голландского сектора акватории Северного моря. Как и в предыдущем эксперименте, имитируя работу интерпретатора, для обучения сети мы выбрали только чистые маски, просмотрев все срезы. В результате было отобрано 700 кросслайнов и 400 инлайнов из ~1600 исходных изображений.
Данный и следующий разделы представляют интерес, в первую очередь, для специалистов по Data Science, поэтому будет использоваться соответствующая терминология.
Для обучения мы выбрали 5% от общего количества срезов, причем, инлайны и кросслайны в равных долях, т.е. 40 + 40. Срезы выбирались равномерно по всему кубу. Для валидации использовалось по 1 срезу между соседними изображениями тренировочной выборки. Таким образом, валидационная выборка состояла из 39 инлайнов и 39 кросслайнов.
В отложенную выборку, на которой и проводилось сравнение результатов, попали 321 инлайн и 621 кросслайн.
Аналогично предыдущему эксперименту, предобработка изображений не проводилась, и использовалась та же архитектура UNet с теми же параметрами обучения.
Целевые маски срезов были представлены как бинарные кубы размерностью HxWx10, где последнее измерение соответствует количеству классов, а каждое значение куба равно 0 или 1 в зависимости от того, принадлежит ли данный пиксель изображения классу соответствующего слоя или нет.
Каждый прогноз сети представлял собой аналогичный куб, каждое значение которого имеет отношение к вероятности принадлежности данного пикселя изображения классу соответствующего слоя. В большинстве случаев это значение преобразовывалось в собственно вероятность применением сигмоиды. Однако не для всех функций потерь это нужно делать, поэтому для последнего слоя сети активация не использовалась. Вместо этого соответствующие преобразования выполнялись в самих функциях.
Для уменьшения влияния произвольности выбора начальных весов на результаты, сеть была обучена в течение 1 эпохи с бинарной кросс-энтропией в качестве функции потерь. Все остальные обучения стартовали с этих полученных весов.
Для эксперимента были выбраны 2 базовых класса функций в 6-ти вариантах:
Binary cross entropy:
Intersection over Union:
Краткое описание перечисленных функций с кодом для Keras даны в статье. Здесь представим самое важное со ссылками (где это возможно) на детальное описание каждой функции.
Для нашего эксперимента важна согласованность функции, используемой во время обучения, с метрикой, по которой мы оцениваем результат прогноза сети на отложенной выборке. Поэтому мы использовали свой код, реализованный на TensorFlow и Numpy, написанный непосредственно по приведенным ниже формулам.
В формулах далее используются обозначения:
Для всех функций, если это не оговорено особо, предполагается, что маска прогноза сети содержит вероятности для каждого пикселя изображения, т.е. значения в интервале (0, 1).
Описание: https://towardsdatascience.com/understanding-binary-cross-entropy-log-loss-a-visual-explanation-a3ac6025181a.

Данная функция стремится приблизить распределение прогноза сети к целевому, штрафуя не только за ошибочные предсказания, но и за неуверенные.
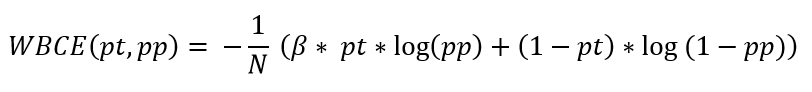
Данная функция совпадает с бинарной кросс-энтропией при значении коэффициента beta = 1. Рекомендуется при сильном дисбалансе классов. При beta > 1 уменьшается количество ложно отрицательных прогнозов (False Negative) и увеличивается полнота (Recall), при beta < 1 уменьшается количество ложно положительных прогнозов (False Positive) и увеличивается точность (Precision).
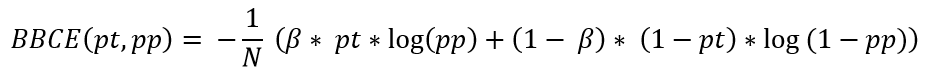
Данная функция похожа на взвешенную кросс-энтропию, но корректирует вклад не только единичных, но и нулевых значений целевой маски. Совпадает (с точностью до константы) с бинарной кросс-энтропией при значении коэффициента beta = 0.5.
Коэффициент Жаккарда (он же Intersection over Union, IoU) определяет меру «похожести» двух областей. То же самое делает Dice index:
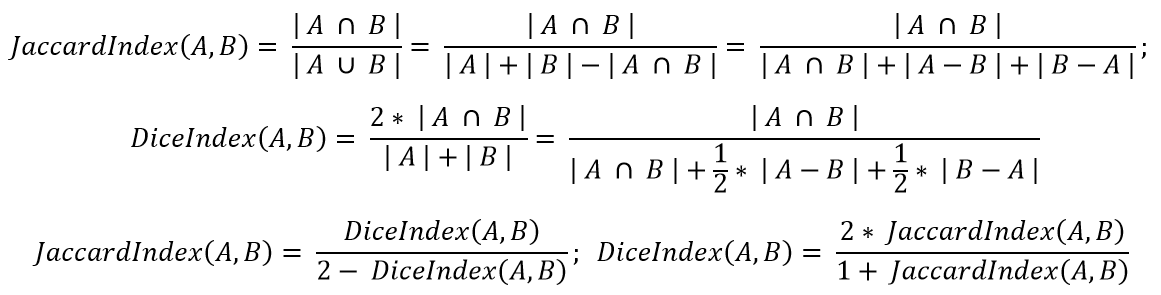
Рассматривать обе эти функции смысла нет. Мы выбрали Жаккард.
Для случая, когда обе области задаются с помощью бинарных масок, представленная выше формула легко переписывается в терминах значений масок:
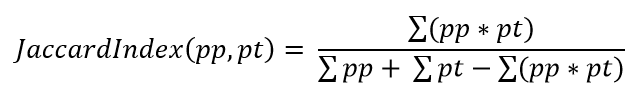
Для небинарных прогнозов оптимизация коэффициента Жаккарда является нетривиальной задачей. Мы будем использовать эту же формулу и для вероятностей в маске прогноза как некую имитацию исходного коэффициента и, соответственно, следующую функцию потерь:

Описание: https://arxiv.org/pdf/1706.05721.pdf

Данная функция является параметризованным вариантом оптимизации коэффициента Жаккарда совпадает с ним при значениях alpha = beta = 1 и с Dice-индексом при alpha = beta = 0.5. При иных ненулевых и несовпадающих значениях мы можем смещать акценты в сторону точности или полноты аналогично тому, как это делалось в функциях взвешенной и сбалансированной кросс-энтропии.
Задача смещения акцентов может быть переписана с помощью одного коэффициента, лежащего в интервале (0, 1). Итоговая функция потерь будет выглядеть следующим образом:
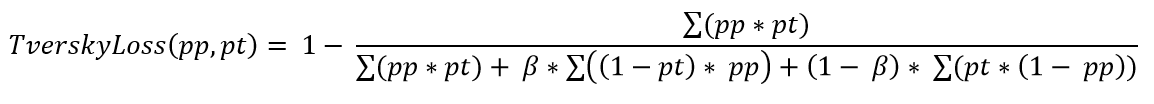
Для данной функции затруднительно привести формулу, поскольку она представляет собой вариант оптимизации коэффициента Жаккарда по алгоритму, основанному на отсортированных ошибках.
Описание функции можно посмотреть здесь, один из вариантов кода – здесь.
Для упрощения сравнения значений и графиков далее под термином «коэффициент Жаккарда» далее мы будем понимать единицу минус собственно коэффициент. Jaccard loss – это один из способов оптимизации такого коэффициента, наряду с Tversky loss и Lovasz loss.
Для выбора наилучшей функции потерь на одном и том же наборе данных нужен критерий оценки. В его качестве мы выбрали среднее/медианное количество компонент связности на получающихся масках. Дополнительно мы использовали коэффициент Жаккарда для прогнозных масок, преобразованных в однослойные по argmax и вновь разделенные уже на бинаризованные слои.
Количество компонент связности (т.е. сплошных пятен одного цвета) на каждом полученном прогнозе является косвенным критерием оценки объема его последующей доработки интерпретатором. Если это значение равно 10, то слои выделены правильно и речь идет максимум о незначительной коррекции горизонтов. Если их ненамного больше, то потребуется лишь «чистка» небольших зон изображения. Если их существенно больше, то все плохо и может даже понадобится полная переразметка.
Коэффициент Жаккарда, в свою очередь, характеризует совпадение зон изображения, отнесенных к одному классу, и их границ.
По результатам экспериментов было выбрано значение параметра beta = 2:

Рисунок 2. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям

Рисунок 3. Статистики для количества компонент связности по части значений параметра beta
По результатам экспериментов было выбрано значение параметра beta = 0.7:

Рисунок 4. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям
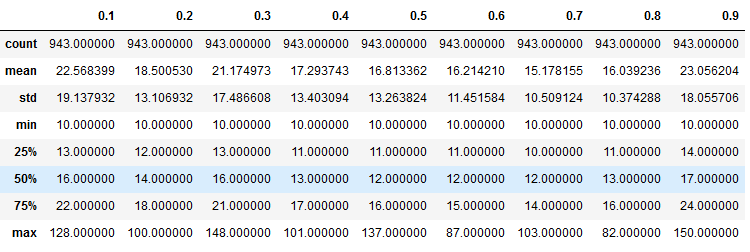
Рисунок 5. Статистики для количества компонент связности
По результатам экспериментов было выбрано значение параметра beta = 0.7:

Рисунок 6. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям

Рисунок 7. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям
Из приведенных рисунков можно сделать два вывода.
Во-первых, выбранные критерии достаточно неплохо коррелируют между собой, т.е. коэффициент Жаккарда согласуется с оценкой объемов необходимой доработки. Во-вторых, поведение кросс-энтропийных функций потерь вполне логично отличается от поведения критериев, т.е. использовать при обучении только лишь данную категорию функций без дополнительной оценки результатов все же не стоит.
Теперь сравним результаты, которые показали выбранные 6 функций потерь на одном и том же наборе данных. Для полноты картины мы добавили предсказания сети, полученной на предыдущем эксперименте.
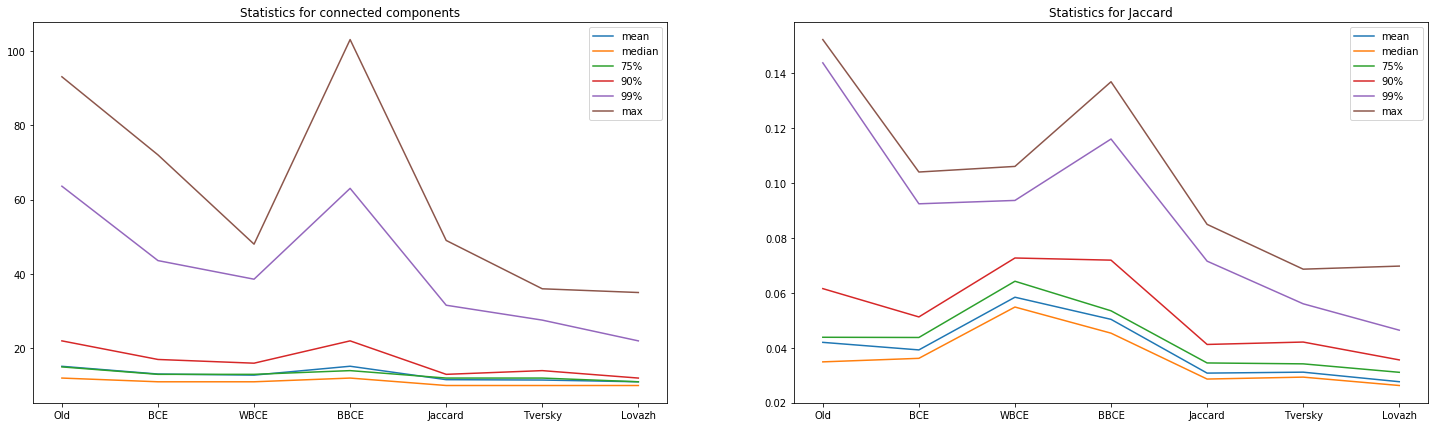
Рисунок 8. Сравнение прогнозов сетей, обученных с разными функциями потерь, по выбранным критериям
Таблица 1. Усредненные значения критериев


Рисунок 9. Сравнение прогнозов сетей по количеству предсказаний с указанным количеством компонент связности
Из представленных диаграмм и таблицы можно сделать следующие выводы относительно использования «сольных» функций потерь:
Сравним визуально прогнозы для срезов с одними из лучших и одними из худших значений Lovazh loss и количества компонент связности. Целевая маска отображена в правом верхнем углу, прогноз, полученный в предыдущем эксперименте – в правом нижнем:

Рисунок 10. Прогнозы сетей для одного из лучших срезов
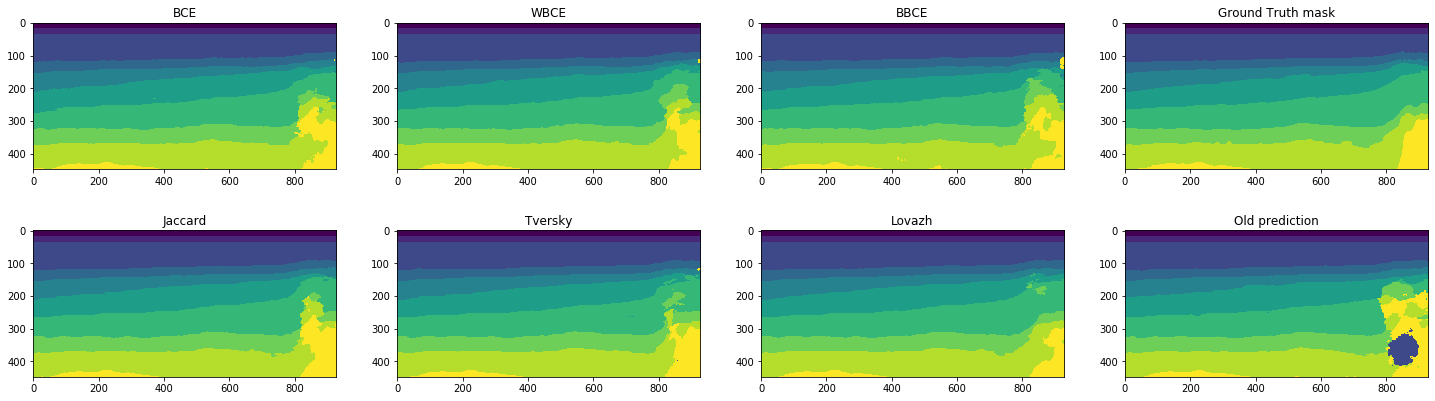
Рисунок 11. Прогнозы сетей для одного из худших срезов
Видно, что все сети одинаково хорошо работают на легко распознаваемых срезах. Но даже на плохо распознаваемом срезе, где ошибаются все сети, прогноз для Lovazh loss визуально лучше прогнозов других сетей. Хотя он и один из худших для этой функции потерь.
Итак, на данном шаге у нас определился явный лидер — Lovazh loss, результаты которого можно охарактеризовать следующим образом:
На данном шаге, только лишь заменив функцию потерь, мы добились существенного улучшения результатов по сравнению с прошлым экспериментом.
Можно ли еще его улучшить путем комбинации разных функций? Проверим.
Комбинирование функций потерь различной природы используется достаточно часто. Однако, нащупать оптимальное сочетание непросто. Наглядный пример – результат предыдущего эксперимента, который оказался даже хуже, чем «сольная» функция. Цель таких сочетаний – улучшить результат за счет оптимизации по разным принципам.
Попробуем перебрать разные варианты выбранной на предыдущем шаге функции с другими, но не со всеми подряд. Ограничимся сочетаниями функций разных типов, в данном случае – с кросс-энтропийными. Рассматривать комбинации однотипных функций смысла нет.
Итого, мы проверили 3 пары с 9-ю возможными коэффициентами каждую (от 0.1\0.9 до 0.9\0.1). На рисунках ниже по оси Х указан коэффициент перед Lovazh loss. Коэффициент перед второй функцией равен единице минус коэффициент перед первой. Левое значение – только кросс-энтропийная функция, правое – только Lovazh loss.
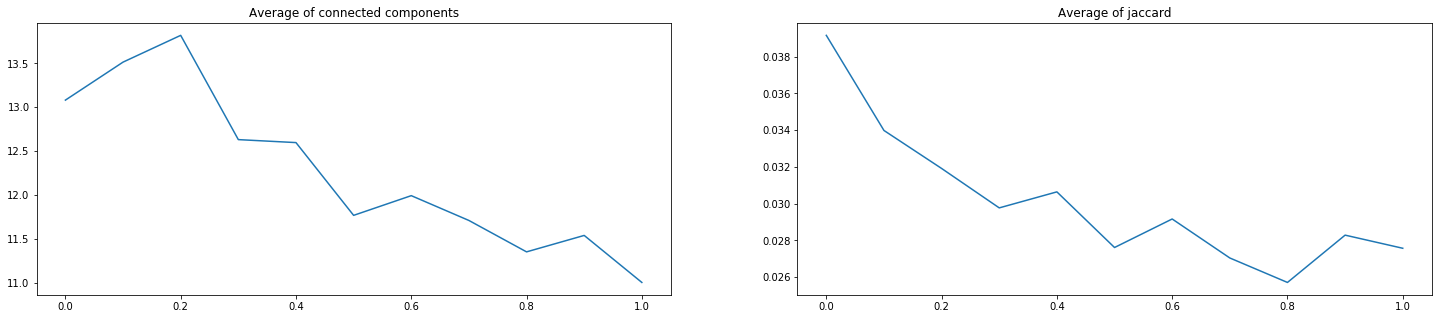
Рисунок 12. Оценки результатов прогноза сетей, обученных на BCE + Lovazh
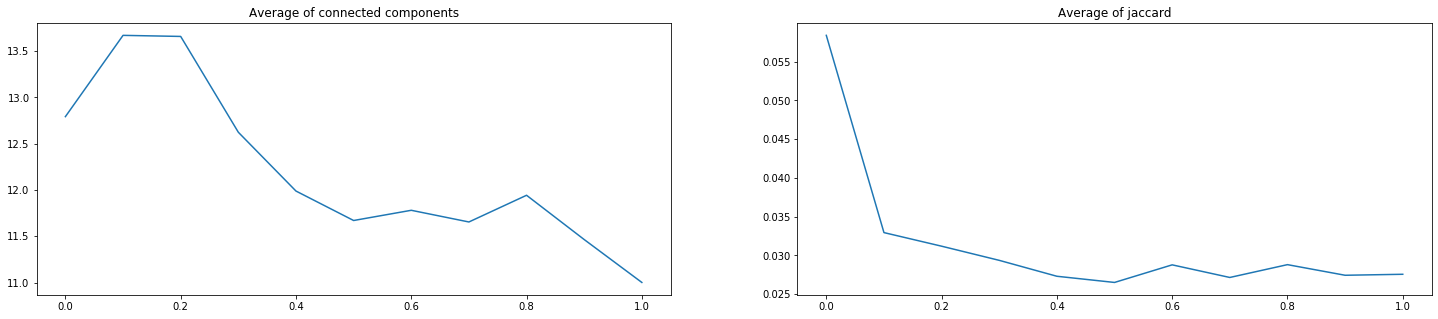
Рисунок 13. Оценки результатов прогноза сетей, обученных на WBCE + Lovazh
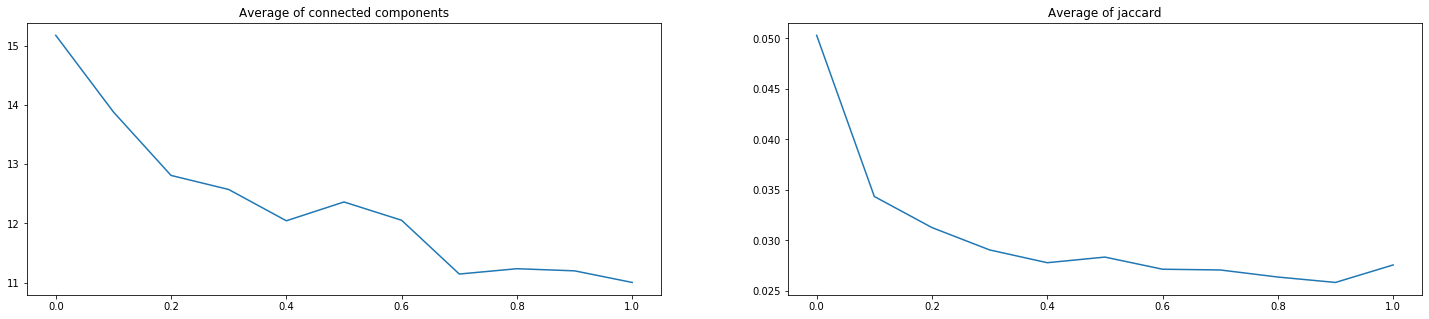
Рисунок 14. Оценки результатов прогноза сетей, обученных на BBCE + Lovazh
Видно, что выбранную «сольную» функцию добавлением кросс-энтропийной улучшить не удалось. Уменьшение некоторых значений коэффициента Жаккарда на 1-2 тысячных может быть важным в условиях соревнований, но не компенсирует для бизнеса ухудшение критерия количества компонент связности.
Чтобы убедиться в типичности поведения комбинации функций разных типов, мы провели аналогичную серию обучения для Jaccard loss. Только для одной пары удалось незначительно улучшить значения обоих критериев одновременно:
0.8 * JaccardLoss + 0.2 * BBCE
Average of connected components: 11.5695 -> 11.2895
Average of Jaccard: 0.0307 -> 0.0283
Но и эти значения хуже, чем «сольная» Lovazh loss.
Таким образом, исследовать сочетания функций разной природы на наших данных есть смысл только в условиях соревнований или при наличии свободного времени и ресурсов. Достичь существенного прироста качества вряд ли удастся.
На этом шаге мы попробовали улучшить выбранную ранее функцию потерь дополнением, разработанным специально для сейсмических данных. Речь идет о регуляризации, описанной в статье: «Neural-networks for geophysicists and their application to seismic data interpretation».
В статье упоминается, что стандартные регуляризации типа weights decay на сейсмических данных работают плохо. Вместо этого предлагается подход, основанный на норме матрицы градиентов, который нацелен на сглаживание границ классов. Подход логичен, если вспомнить, что границы геологических слоев и должны быть гладкими.
Однако при использовании такой регуляризации стоит ожидать некоторого ухудшения результатов по критерию Жаккарда, т.к. сглаженные границы классов будут в меньшей степени совпадать с возможными резкими переходами, полученными при ручной разметке. Но у нас для проверки есть еще один критерий – по количеству компонент связности.
Мы обучили 13 сетей с описанной в статье регуляризацией и коэффициентом перед ней, принимающим значения от 0.1 до 0.0001. На рисунках ниже представлена часть оценок по обоим критериям.

Рисунок 15. Сравнение качества прогноза сети по выбранным критериям

Рисунок 16. Статистики для количества компонент связности по части значений коэффициента перед регуляризацией
Видно, что регуляризация с коэффициентом 0.025 существенно уменьшила статистики для критерия количества компонент связности. Однако, критерий Жаккарда при этом ожидаемо возрос до 0.0357. Впрочем, это незначительный рост по сравнению с сокращением объема ручной доработки.

Рисунок 17. Сравнение прогнозов сетей по количеству предсказаний с указанным количеством компонент связности
Напоследок сравним границы классов на целевых и предсказанных масках для выбранного ранее наихудшего среза.

Рисунок 18. Прогноз сети для одного из худших срезов
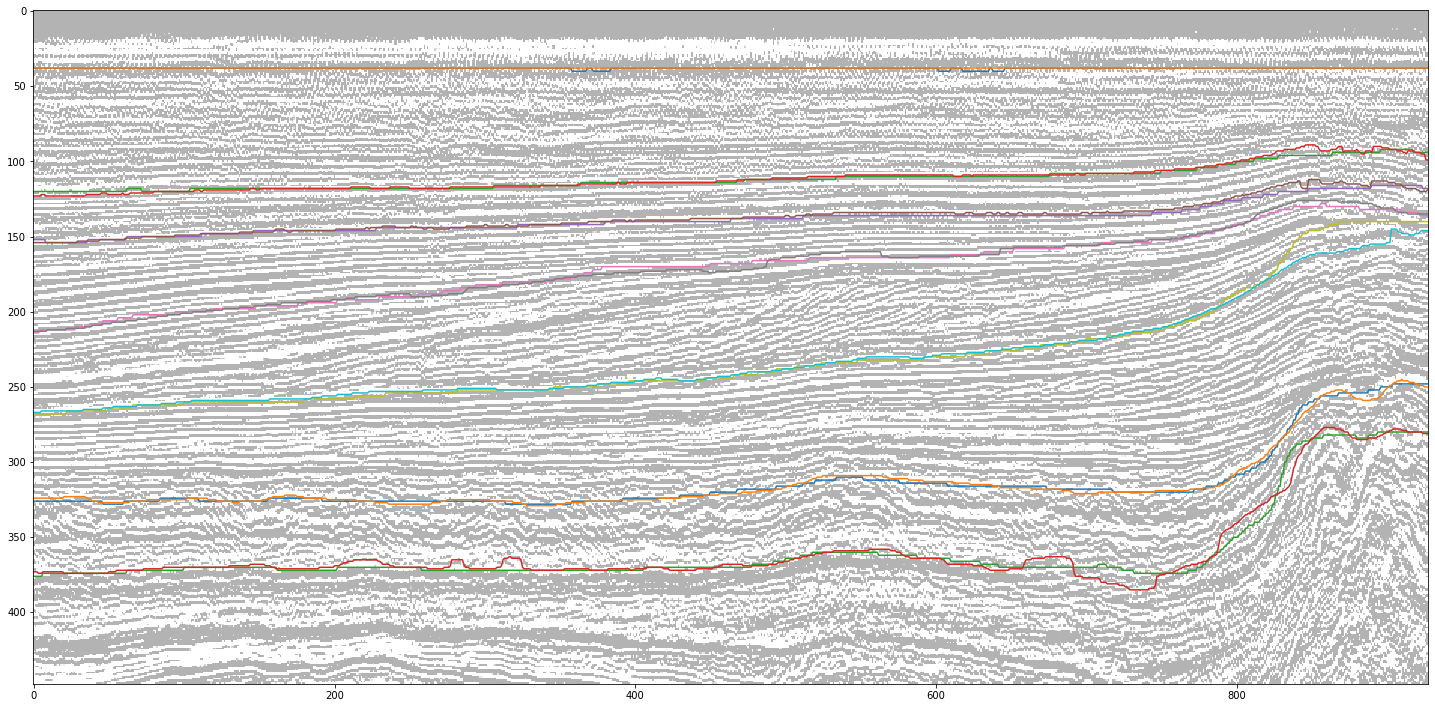
Рисунок 19. Наложение части горизонтов целевой маски и прогноза
Как видно из рисунков, прогнозная маска, конечно, кое-где ошибается, но при этом сглаживает осцилляции горизонтов целевой, т.е. исправляет незначительные погрешности исходной разметки.
Итоговые характеристики выбранной функции потерь с регуляризацией:
Рассмотрены 2 базовых класса функций – Binary cross entropy и Intersection over Union – в 6-ти вариантах с подбором параметров, а также комбинации функций разных классов. Дополнительно рассмотрена регуляризация функции потерь.
Спойлер: удалось существенно улучшить качество прогноза сети.

Бизнес-цели исследования
Не будем повторять описание специфики проведения сейсморазведки, получаемых данных и задачи их интерпретации. Все это описано в нашей предыдущей статье.
На идею данного исследования нас натолкнули результаты соревнования по поиску солевых отложений на 2D-срезах. По отзывам участников соревнования, при решении этой задачи использовался целый зоопарк различных функций потерь, причем, с разным успехом.
Поэтому мы и задались вопросом – действительно ли для подобных задач на таких данных подбор функции потерь может дать существенный выигрыш в качестве? Или это характерно только для условий соревнования, когда идет борьба за четвертый-пятый знак после запятой для заранее определенной организаторами метрики?
Обычно в задачах, решаемых с помощью нейронных сетей, настройка процесса обучения основывается большей частью на опыте исследователя и некоторых эвристиках. Например, для задач сегментации изображений чаще всего применяются функции потерь, основанные на оценке совпадения форм распознанных зон, так называемые Intersection over Union.
Интуитивно, основываясь на понимании поведения и результатах исследований, такого рода функции дадут лучший результат, чем те, которые не заточены под изображения, как например кросс-энтропийные. Тем не менее, эксперименты в поисках оптимального варианта для такого типа задач в целом и каждой задачи индивидуально продолжаются.
Данные сейсморазведки, подготовленные для интерпретации, обладают рядом особенностей, которые могут оказать существенное влияние на поведение функции потерь. Например, горизонты, разделяющие геологические слои, плавные, более резко изменяющиеся только в местах разломов. Кроме того, выделяемые зоны имеют достаточно большую относительно изображения площадь, т.е. маленькие пятна на результатах интерпретации чаще всего считаются ошибкой распознавания.
В рамках данного эксперимента мы попытались найти ответы на следующие локальные вопросы:
- Действительно ли для рассмотренной ниже задачи наилучший результат даст функция потерь класса Intersection over Union? Вроде ответ очевиден, но какая именно? И насколько лучший с точки зрения бизнеса?
- Можно ли еще улучшить результаты, комбинируя функции различных классов? Например, Intersection over Union и кросс-энтропийную с разными весами.
- Можно ли еще улучшить результаты, добавляя к функции потерь разные дополнения, разработанные специально для сейсмических данных?
И на более глобальный вопрос:
А стоит ли заморачиваться подбором функции потерь для задач интерпретации сейсмических данных, или полученный выигрыш в качестве не сопоставим с потерями времени на проведение таких исследований? Может, стоит интуитивно выбрать любую функцию и потратить силы на подбор более значимых параметров обучения?
Общее описание эксперимента и использованных данных
Для эксперимента мы взяли все ту же задачу выделения геологических слоев на 2D-срезах сейсмического куба (см. рисунок 1).

Рисунок 1. Пример 2D-среза (слева) и результата разметки соответствующих ему геологических слоев (справа) (источник)
И тот же набор полностью размеченных данных из голландского сектора акватории Северного моря. Исходные сейсмические данные представлены на сайте Open Seismic Repository: Project Netherlands Offshore F3 Block. Их краткое описание можно найти в статье Silva et al. «Netherlands Dataset: A New Public Dataset for Machine Learning in Seismic Interpretation».
Поскольку в нашем случае речь идет о 2D-срезах, мы использовали не исходный 3D-куб, а уже сделанную «нарезку», доступную здесь: Netherlands F3 Interpretation Dataset.
В процессе эксперимента мы решили следующие задачи:
- Просмотрели исходные данные и отобрали срезы, которые по качеству ближе всего к ручной разметке (аналогично предыдущему эксперименту).
- Зафиксировали архитектуру нейронной сети, методику и параметры обучения и принцип выбора срезов для обучения и валидации (аналогично предыдущему эксперименту).
- Выбрали исследуемые функции потерь.
- Выбрали наилучшие параметры для параметризованных функций потерь.
- Обучили нейронные сети с разными функциями на одном и том же объеме данных и выбрали наилучшую функцию.
- Обучили нейронные сети с разными комбинациями выбранной функции с функциями другого класса на том же объеме данных.
- Обучили нейронные сети с регуляризацией выбранной функции на том же объеме данных.
Для сравнения мы использовали результаты предыдущего эксперимента, в котором функция потерь была выбрана исключительно интуитивно и представляла собой комбинацию функций разных классов с коэффициентами, так же выбранными «на глаз».
Результаты данного эксперимента в виде оценочных метрик и предсказанных сетями масок срезов представлены далее.
Задача 1. Отбор данных
В качестве исходных данных мы использовали готовые инлайны и кросслайны сейсмического куба из голландского сектора акватории Северного моря. Как и в предыдущем эксперименте, имитируя работу интерпретатора, для обучения сети мы выбрали только чистые маски, просмотрев все срезы. В результате было отобрано 700 кросслайнов и 400 инлайнов из ~1600 исходных изображений.
Задача 2. Фиксирование параметров эксперимента
Данный и следующий разделы представляют интерес, в первую очередь, для специалистов по Data Science, поэтому будет использоваться соответствующая терминология.
Для обучения мы выбрали 5% от общего количества срезов, причем, инлайны и кросслайны в равных долях, т.е. 40 + 40. Срезы выбирались равномерно по всему кубу. Для валидации использовалось по 1 срезу между соседними изображениями тренировочной выборки. Таким образом, валидационная выборка состояла из 39 инлайнов и 39 кросслайнов.
В отложенную выборку, на которой и проводилось сравнение результатов, попали 321 инлайн и 621 кросслайн.
Аналогично предыдущему эксперименту, предобработка изображений не проводилась, и использовалась та же архитектура UNet с теми же параметрами обучения.
Целевые маски срезов были представлены как бинарные кубы размерностью HxWx10, где последнее измерение соответствует количеству классов, а каждое значение куба равно 0 или 1 в зависимости от того, принадлежит ли данный пиксель изображения классу соответствующего слоя или нет.
Каждый прогноз сети представлял собой аналогичный куб, каждое значение которого имеет отношение к вероятности принадлежности данного пикселя изображения классу соответствующего слоя. В большинстве случаев это значение преобразовывалось в собственно вероятность применением сигмоиды. Однако не для всех функций потерь это нужно делать, поэтому для последнего слоя сети активация не использовалась. Вместо этого соответствующие преобразования выполнялись в самих функциях.
Для уменьшения влияния произвольности выбора начальных весов на результаты, сеть была обучена в течение 1 эпохи с бинарной кросс-энтропией в качестве функции потерь. Все остальные обучения стартовали с этих полученных весов.
Задача 3. Выбор функций потерь
Для эксперимента были выбраны 2 базовых класса функций в 6-ти вариантах:
Binary cross entropy:
- binary cross entropy;
- weighted binary cross entropy;
- balanced binary cross entropy.
Intersection over Union:
- Jaccard loss;
- Tversky loss;
- Lovasz loss.
Краткое описание перечисленных функций с кодом для Keras даны в статье. Здесь представим самое важное со ссылками (где это возможно) на детальное описание каждой функции.
Для нашего эксперимента важна согласованность функции, используемой во время обучения, с метрикой, по которой мы оцениваем результат прогноза сети на отложенной выборке. Поэтому мы использовали свой код, реализованный на TensorFlow и Numpy, написанный непосредственно по приведенным ниже формулам.
В формулах далее используются обозначения:
- pt – для бинарной целевой маски (Ground Truth);
- pp – для маски прогноза сети.
Для всех функций, если это не оговорено особо, предполагается, что маска прогноза сети содержит вероятности для каждого пикселя изображения, т.е. значения в интервале (0, 1).
Binary cross entropy
Описание: https://towardsdatascience.com/understanding-binary-cross-entropy-log-loss-a-visual-explanation-a3ac6025181a.

Данная функция стремится приблизить распределение прогноза сети к целевому, штрафуя не только за ошибочные предсказания, но и за неуверенные.
Weighted binary cross entropy
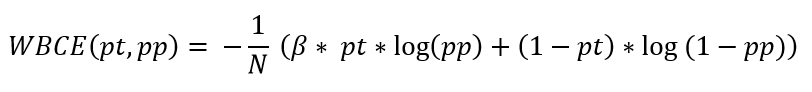
Данная функция совпадает с бинарной кросс-энтропией при значении коэффициента beta = 1. Рекомендуется при сильном дисбалансе классов. При beta > 1 уменьшается количество ложно отрицательных прогнозов (False Negative) и увеличивается полнота (Recall), при beta < 1 уменьшается количество ложно положительных прогнозов (False Positive) и увеличивается точность (Precision).
Balanced binary cross entropy
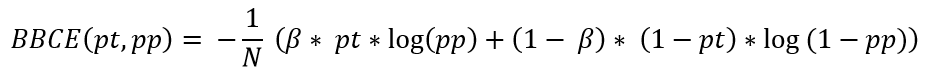
Данная функция похожа на взвешенную кросс-энтропию, но корректирует вклад не только единичных, но и нулевых значений целевой маски. Совпадает (с точностью до константы) с бинарной кросс-энтропией при значении коэффициента beta = 0.5.
Jaccard loss
Коэффициент Жаккарда (он же Intersection over Union, IoU) определяет меру «похожести» двух областей. То же самое делает Dice index:
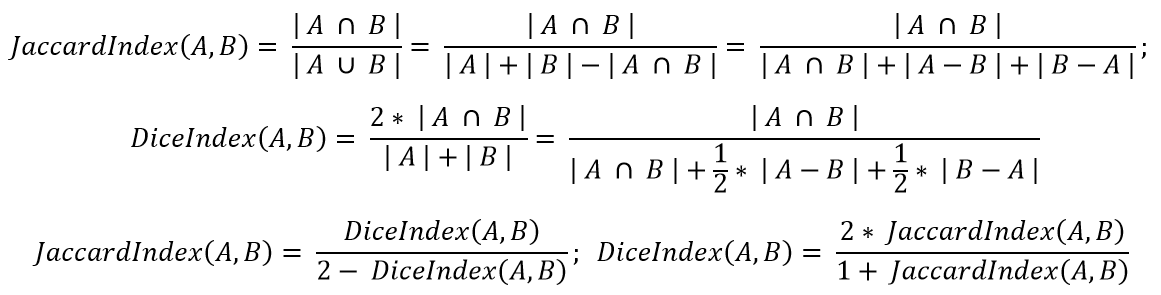
Рассматривать обе эти функции смысла нет. Мы выбрали Жаккард.
Для случая, когда обе области задаются с помощью бинарных масок, представленная выше формула легко переписывается в терминах значений масок:
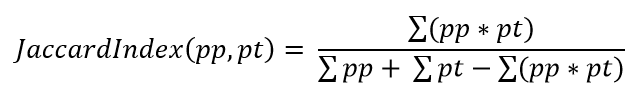
Для небинарных прогнозов оптимизация коэффициента Жаккарда является нетривиальной задачей. Мы будем использовать эту же формулу и для вероятностей в маске прогноза как некую имитацию исходного коэффициента и, соответственно, следующую функцию потерь:

Tversky loss
Описание: https://arxiv.org/pdf/1706.05721.pdf

Данная функция является параметризованным вариантом оптимизации коэффициента Жаккарда совпадает с ним при значениях alpha = beta = 1 и с Dice-индексом при alpha = beta = 0.5. При иных ненулевых и несовпадающих значениях мы можем смещать акценты в сторону точности или полноты аналогично тому, как это делалось в функциях взвешенной и сбалансированной кросс-энтропии.
Задача смещения акцентов может быть переписана с помощью одного коэффициента, лежащего в интервале (0, 1). Итоговая функция потерь будет выглядеть следующим образом:
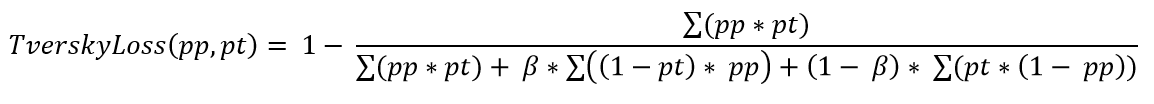
Lovasz loss
Для данной функции затруднительно привести формулу, поскольку она представляет собой вариант оптимизации коэффициента Жаккарда по алгоритму, основанному на отсортированных ошибках.
Описание функции можно посмотреть здесь, один из вариантов кода – здесь.
Важное пояснение!
Для упрощения сравнения значений и графиков далее под термином «коэффициент Жаккарда» далее мы будем понимать единицу минус собственно коэффициент. Jaccard loss – это один из способов оптимизации такого коэффициента, наряду с Tversky loss и Lovasz loss.
Задача 4. Выбор наилучших параметров для параметризованных функций потерь
Для выбора наилучшей функции потерь на одном и том же наборе данных нужен критерий оценки. В его качестве мы выбрали среднее/медианное количество компонент связности на получающихся масках. Дополнительно мы использовали коэффициент Жаккарда для прогнозных масок, преобразованных в однослойные по argmax и вновь разделенные уже на бинаризованные слои.
Количество компонент связности (т.е. сплошных пятен одного цвета) на каждом полученном прогнозе является косвенным критерием оценки объема его последующей доработки интерпретатором. Если это значение равно 10, то слои выделены правильно и речь идет максимум о незначительной коррекции горизонтов. Если их ненамного больше, то потребуется лишь «чистка» небольших зон изображения. Если их существенно больше, то все плохо и может даже понадобится полная переразметка.
Коэффициент Жаккарда, в свою очередь, характеризует совпадение зон изображения, отнесенных к одному классу, и их границ.
Weighted binary cross entropy
По результатам экспериментов было выбрано значение параметра beta = 2:

Рисунок 2. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям

Рисунок 3. Статистики для количества компонент связности по части значений параметра beta
Balanced binary cross entropy
По результатам экспериментов было выбрано значение параметра beta = 0.7:

Рисунок 4. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям

Рисунок 5. Статистики для количества компонент связности
Tversky loss
По результатам экспериментов было выбрано значение параметра beta = 0.7:

Рисунок 6. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям

Рисунок 7. Сравнение качества прогноза сети по основной функции потерь и выбранным критериям
Из приведенных рисунков можно сделать два вывода.
Во-первых, выбранные критерии достаточно неплохо коррелируют между собой, т.е. коэффициент Жаккарда согласуется с оценкой объемов необходимой доработки. Во-вторых, поведение кросс-энтропийных функций потерь вполне логично отличается от поведения критериев, т.е. использовать при обучении только лишь данную категорию функций без дополнительной оценки результатов все же не стоит.
Задача 5. Выбор наилучшей функции потерь
Теперь сравним результаты, которые показали выбранные 6 функций потерь на одном и том же наборе данных. Для полноты картины мы добавили предсказания сети, полученной на предыдущем эксперименте.

Рисунок 8. Сравнение прогнозов сетей, обученных с разными функциями потерь, по выбранным критериям
Таблица 1. Усредненные значения критериев


Рисунок 9. Сравнение прогнозов сетей по количеству предсказаний с указанным количеством компонент связности
Из представленных диаграмм и таблицы можно сделать следующие выводы относительно использования «сольных» функций потерь:
- В нашем случае «Жаккардовые» функции класса Intersection over Union действительно показывают лучшие значения, чем кросс-энтропийные. Причем, существенно лучшие.
- Среди выбранных подходов к оптимизации функции потерь на основе коэффициента Жаккарда лучший результат показала Lovazh loss.
Сравним визуально прогнозы для срезов с одними из лучших и одними из худших значений Lovazh loss и количества компонент связности. Целевая маска отображена в правом верхнем углу, прогноз, полученный в предыдущем эксперименте – в правом нижнем:

Рисунок 10. Прогнозы сетей для одного из лучших срезов

Рисунок 11. Прогнозы сетей для одного из худших срезов
Видно, что все сети одинаково хорошо работают на легко распознаваемых срезах. Но даже на плохо распознаваемом срезе, где ошибаются все сети, прогноз для Lovazh loss визуально лучше прогнозов других сетей. Хотя он и один из худших для этой функции потерь.
Итак, на данном шаге у нас определился явный лидер — Lovazh loss, результаты которого можно охарактеризовать следующим образом:
- около 60% прогнозов близки к идеальным, т.е. потребуют не более чем корректировки отдельных участков горизонтов;
- еще примерно 30% прогнозов содержат не более 2 лишних пятен, т.е. требуют незначительной доработки;
- примерно 1% прогнозов содержит от 10 до 25 лишних пятен, т.е. требует существенной доработки.
На данном шаге, только лишь заменив функцию потерь, мы добились существенного улучшения результатов по сравнению с прошлым экспериментом.
Можно ли еще его улучшить путем комбинации разных функций? Проверим.
Задача 6. Выбор наилучшей комбинации функции потерь
Комбинирование функций потерь различной природы используется достаточно часто. Однако, нащупать оптимальное сочетание непросто. Наглядный пример – результат предыдущего эксперимента, который оказался даже хуже, чем «сольная» функция. Цель таких сочетаний – улучшить результат за счет оптимизации по разным принципам.
Попробуем перебрать разные варианты выбранной на предыдущем шаге функции с другими, но не со всеми подряд. Ограничимся сочетаниями функций разных типов, в данном случае – с кросс-энтропийными. Рассматривать комбинации однотипных функций смысла нет.
Итого, мы проверили 3 пары с 9-ю возможными коэффициентами каждую (от 0.1\0.9 до 0.9\0.1). На рисунках ниже по оси Х указан коэффициент перед Lovazh loss. Коэффициент перед второй функцией равен единице минус коэффициент перед первой. Левое значение – только кросс-энтропийная функция, правое – только Lovazh loss.

Рисунок 12. Оценки результатов прогноза сетей, обученных на BCE + Lovazh

Рисунок 13. Оценки результатов прогноза сетей, обученных на WBCE + Lovazh

Рисунок 14. Оценки результатов прогноза сетей, обученных на BBCE + Lovazh
Видно, что выбранную «сольную» функцию добавлением кросс-энтропийной улучшить не удалось. Уменьшение некоторых значений коэффициента Жаккарда на 1-2 тысячных может быть важным в условиях соревнований, но не компенсирует для бизнеса ухудшение критерия количества компонент связности.
Чтобы убедиться в типичности поведения комбинации функций разных типов, мы провели аналогичную серию обучения для Jaccard loss. Только для одной пары удалось незначительно улучшить значения обоих критериев одновременно:
0.8 * JaccardLoss + 0.2 * BBCE
Average of connected components: 11.5695 -> 11.2895
Average of Jaccard: 0.0307 -> 0.0283
Но и эти значения хуже, чем «сольная» Lovazh loss.
Таким образом, исследовать сочетания функций разной природы на наших данных есть смысл только в условиях соревнований или при наличии свободного времени и ресурсов. Достичь существенного прироста качества вряд ли удастся.
Задача 7. Регуляризация наилучшей функции потерь
На этом шаге мы попробовали улучшить выбранную ранее функцию потерь дополнением, разработанным специально для сейсмических данных. Речь идет о регуляризации, описанной в статье: «Neural-networks for geophysicists and their application to seismic data interpretation».
В статье упоминается, что стандартные регуляризации типа weights decay на сейсмических данных работают плохо. Вместо этого предлагается подход, основанный на норме матрицы градиентов, который нацелен на сглаживание границ классов. Подход логичен, если вспомнить, что границы геологических слоев и должны быть гладкими.
Однако при использовании такой регуляризации стоит ожидать некоторого ухудшения результатов по критерию Жаккарда, т.к. сглаженные границы классов будут в меньшей степени совпадать с возможными резкими переходами, полученными при ручной разметке. Но у нас для проверки есть еще один критерий – по количеству компонент связности.
Мы обучили 13 сетей с описанной в статье регуляризацией и коэффициентом перед ней, принимающим значения от 0.1 до 0.0001. На рисунках ниже представлена часть оценок по обоим критериям.

Рисунок 15. Сравнение качества прогноза сети по выбранным критериям

Рисунок 16. Статистики для количества компонент связности по части значений коэффициента перед регуляризацией
Видно, что регуляризация с коэффициентом 0.025 существенно уменьшила статистики для критерия количества компонент связности. Однако, критерий Жаккарда при этом ожидаемо возрос до 0.0357. Впрочем, это незначительный рост по сравнению с сокращением объема ручной доработки.

Рисунок 17. Сравнение прогнозов сетей по количеству предсказаний с указанным количеством компонент связности
Напоследок сравним границы классов на целевых и предсказанных масках для выбранного ранее наихудшего среза.

Рисунок 18. Прогноз сети для одного из худших срезов

Рисунок 19. Наложение части горизонтов целевой маски и прогноза
Как видно из рисунков, прогнозная маска, конечно, кое-где ошибается, но при этом сглаживает осцилляции горизонтов целевой, т.е. исправляет незначительные погрешности исходной разметки.
Итоговые характеристики выбранной функции потерь с регуляризацией:
- около 87% прогнозов близки к идеальным, т.е. потребуют не более чем корректировки отдельных участков горизонтов;
- еще примерно 10% прогнозов содержат 1 лишнее пятно, т.е. требуют незначительной доработки;
- около 3% прогнозов содержит от 2 до 5 лишних пятен, т.е. требуют чуть более существенной доработки.
Выводы
- Только за счет настройки одного параметра обучения – функции потерь – мы смогли существенно улучшить качество прогноза сети и уменьшить объем необходимой доработки примерно втрое.
- При острой нехватке времени на эксперименты стоит брать любую из функций потерь класса Intersection over Union (на рассмотренной задаче лучшей оказалась Lovazh loss) с подбором коэффициента для сглаживающей регуляризации. При наличии времени можно поэкспериментировать с комбинациями этого класса функций с кросс-энтропийными, но шансы на существенное увеличение качества невелики.
- Такой подход хорош для бизнес-задач, поскольку исправляет незначительные погрешности исходной разметки. Но регуляризация вряд ли будет полезной в условиях соревнований, т.к. ухудшает оценку по целевой метрике.
Список использованных источников:
- Reinaldo Mozart Silva, Lais Baroni, Rodrigo S. Ferreira, Daniel Civitarese, Daniela Szwarcman, Emilio Vital Brazil. Netherlands Dataset: A New Public Dataset for Machine Learning in Seismic Interpretation
- Lars Nieradzik. Losses for Image Segmentation
- Daniel Godoy. Understanding binary cross-entropy / log loss: a visual explanation
- Seyed Sadegh Mohseni Salehi, Deniz Erdogmus, and Ali Gholipour. Tversky loss function for image segmentation using 3D fully convolutional deep networks
- Maxim Berman, Amal Rannen Triki, Matthew B. Blaschko. The Lovasz-Softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks
- Bas Peters, Eldad Haber, and Justin Granek. Neural-networks for geophysicists and their application to seismic data interpretation

