Очень часто при цифровой обработке сигналов необходимо вычислить длину вектора, обычно это делается по формуле A=SQRТ(X^2+Y^2). Здесь возвести в квадрат значение не сложно, но операция вычисления квадратного корня не является простой операцией, особенно для микроконтроллеров. Кроме того, алгоритмы вычисления корня выполняются не стабильное время, и для алгоритмов, в которых таких вычислений много, становится сложно прогнозировать время, необходимое для вычислений.
С такой задачей столкнулся и я. О том, как я отказался от процедуры вычисления корня, читайте ниже.
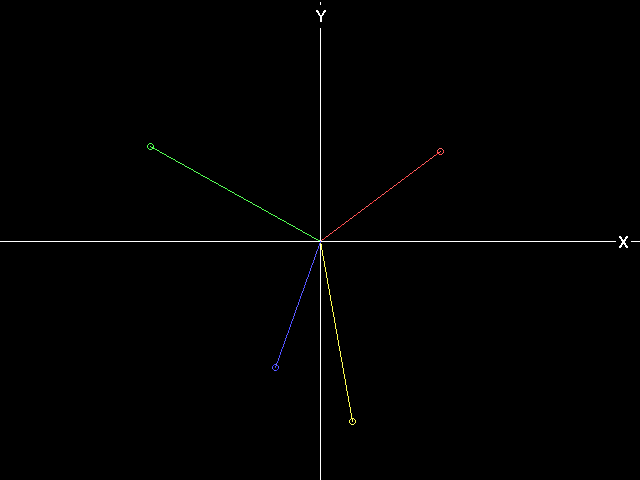
Для начала рассмотрим четыре вектора, они лежат в разных четвертях.
Сведем все в одну четверть — в первую. Для этого возьмем координату Y и если она отрицательная, то превратим ее в положительную. В случае если она и так положительная, то оставим все без изменений.
На самом деле, поскольку у меня абсолютные координаты и значения указаны в целых числах без знака, то вычислим модуль.
Если Y>2047, то Y=Y-2047
Если Y<=2047, то Y=2047-Y
Здесь 2047 — это виртуальный ноль, поскольку в проекте с которым я работал, когда изобретал этот велосипед, были АЦП 12 бит.
Посмотрим, что произошло.
И сделаем тоже самое для координаты X.
Если X>2047, то X=X-2047
Если X<=2047, то X=2047-X
Кстати стоит заметить, что от двух 12-битных значений, осталось два 11-битных.
Теперь все векторы находятся в первой четверти, но ведь их длина, которую мы ищем, не изменилась.
Следующий этап преобразований: «вывернем вокруг оси 45 градусов».
Векторы могут иметь угол от нуля и до 90 градусов, при этом если в координатах вектора Y>X, то угол вектора лежит в области 45-90 градусов, а если Y<X, то угол вектора меньше 45 градусов. Ну и если X=Y, то угол вектора равен 45 градусам.
Сведем векторы к 45 градусам.
Если Y>X, то TEMP=Y, Y=X, X=TEMP (меняем X и Y местами).
Если Y<=X, то ничего не делаем.
Смотрим, что произошло. Все векторы лежат в диапазоне углов от 0 и до 45 градусов.
Хочу заметить, что на этом этапе, у меня была идея проверить угол на 22,5 градуса и опять развернуть. А потом сделать проверку и выворачивание на 12,25 градуса. И так далее, пока вектор не «ляжет» на ось X, а тогда его длина и будет определяться координатой X, а Y станет равен нулю.
Но я не пошел этим путем, я сделал ставку на другой метод, и как оказалось впоследствии, не прогадал.
Если разделить Y на X, а потом взять арктангенс из этого частного, то получим угол. А если разделить X на косинус этого угла, то получим длину вектора.
Итак, длина вектора равна A=X/COS(ATAN(Y/X))
Казалось сложно, когда я думал, что надо получать угол по таблице арктангенсов, а потом получать коэффициент по таблице косинусов.
Но все обошлось. Я решил, что можно сразу сделать таблицу, где отношение Y/X адресует ячейку, а в ней «лежит» коэффициент, на который надо разделить X, чтобы получить длину вектора.
A=X/K; где K=COS(ATAN(Y/X))
Но умножать проще чем делить, поэтому:
A=X*K; где K=1/COS(ATAN(Y/X))
Понятно, что все K, для всех (Y/X), должны быть посчитаны заранее.
Просчитанная таблица содержит 2048 значений, каждое из которых 16 бит. То есть 4кБ данных.
Таблица
Magnitude_Table
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802
DCW 0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802
DCW 0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0803,0x0803
DCW 0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803
DCW 0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803
DCW 0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804
DCW 0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0805
DCW 0x0805,0x0805,0x0805,0x0805,0x0805,0x0805,0x0805,0x0805
DCW 0x0805,0x0805,0x0805,0x0805,0x0806,0x0806,0x0806,0x0806
DCW 0x0806,0x0806,0x0806,0x0806,0x0806,0x0806,0x0806,0x0806
DCW 0x0806,0x0807,0x0807,0x0807,0x0807,0x0807,0x0807,0x0807
DCW 0x0807,0x0807,0x0807,0x0807,0x0807,0x0808,0x0808,0x0808
DCW 0x0808,0x0808,0x0808,0x0808,0x0808,0x0808,0x0808,0x0808
DCW 0x0809,0x0809,0x0809,0x0809,0x0809,0x0809,0x0809,0x0809
DCW 0x0809,0x0809,0x080A,0x080A,0x080A,0x080A,0x080A,0x080A
DCW 0x080A,0x080A,0x080A,0x080A,0x080B,0x080B,0x080B,0x080B
DCW 0x080B,0x080B,0x080B,0x080B,0x080B,0x080B,0x080C,0x080C
DCW 0x080C,0x080C,0x080C,0x080C,0x080C,0x080C,0x080C,0x080D
DCW 0x080D,0x080D,0x080D,0x080D,0x080D,0x080D,0x080D,0x080E
DCW 0x080E,0x080E,0x080E,0x080E,0x080E,0x080E,0x080E,0x080E
DCW 0x080F,0x080F,0x080F,0x080F,0x080F,0x080F,0x080F,0x080F
DCW 0x0810,0x0810,0x0810,0x0810,0x0810,0x0810,0x0810,0x0810
DCW 0x0811,0x0811,0x0811,0x0811,0x0811,0x0811,0x0811,0x0811
DCW 0x0812,0x0812,0x0812,0x0812,0x0812,0x0812,0x0812,0x0813
DCW 0x0813,0x0813,0x0813,0x0813,0x0813,0x0813,0x0814,0x0814
DCW 0x0814,0x0814,0x0814,0x0814,0x0814,0x0814,0x0815,0x0815
DCW 0x0815,0x0815,0x0815,0x0815,0x0816,0x0816,0x0816,0x0816
DCW 0x0816,0x0816,0x0816,0x0817,0x0817,0x0817,0x0817,0x0817
DCW 0x0817,0x0817,0x0818,0x0818,0x0818,0x0818,0x0818,0x0818
DCW 0x0819,0x0819,0x0819,0x0819,0x0819,0x0819,0x0819,0x081A
DCW 0x081A,0x081A,0x081A,0x081A,0x081A,0x081B,0x081B,0x081B
DCW 0x081B,0x081B,0x081B,0x081C,0x081C,0x081C,0x081C,0x081C
DCW 0x081C,0x081D,0x081D,0x081D,0x081D,0x081D,0x081D,0x081E
DCW 0x081E,0x081E,0x081E,0x081E,0x081E,0x081F,0x081F,0x081F
DCW 0x081F,0x081F,0x081F,0x0820,0x0820,0x0820,0x0820,0x0820
DCW 0x0820,0x0821,0x0821,0x0821,0x0821,0x0821,0x0822,0x0822
DCW 0x0822,0x0822,0x0822,0x0822,0x0823,0x0823,0x0823,0x0823
DCW 0x0823,0x0824,0x0824,0x0824,0x0824,0x0824,0x0824,0x0825
DCW 0x0825,0x0825,0x0825,0x0825,0x0826,0x0826,0x0826,0x0826
DCW 0x0826,0x0827,0x0827,0x0827,0x0827,0x0827,0x0828,0x0828
DCW 0x0828,0x0828,0x0828,0x0829,0x0829,0x0829,0x0829,0x0829
DCW 0x082A,0x082A,0x082A,0x082A,0x082A,0x082B,0x082B,0x082B
DCW 0x082B,0x082B,0x082C,0x082C,0x082C,0x082C,0x082C,0x082D
DCW 0x082D,0x082D,0x082D,0x082D,0x082E,0x082E,0x082E,0x082E
DCW 0x082E,0x082F,0x082F,0x082F,0x082F,0x0830,0x0830,0x0830
DCW 0x0830,0x0830,0x0831,0x0831,0x0831,0x0831,0x0831,0x0832
DCW 0x0832,0x0832,0x0832,0x0833,0x0833,0x0833,0x0833,0x0833
DCW 0x0834,0x0834,0x0834,0x0834,0x0835,0x0835,0x0835,0x0835
DCW 0x0835,0x0836,0x0836,0x0836,0x0836,0x0837,0x0837,0x0837
DCW 0x0837,0x0837,0x0838,0x0838,0x0838,0x0838,0x0839,0x0839
DCW 0x0839,0x0839,0x083A,0x083A,0x083A,0x083A,0x083A,0x083B
DCW 0x083B,0x083B,0x083B,0x083C,0x083C,0x083C,0x083C,0x083D
DCW 0x083D,0x083D,0x083D,0x083E,0x083E,0x083E,0x083E,0x083F
DCW 0x083F,0x083F,0x083F,0x0840,0x0840,0x0840,0x0840,0x0840
DCW 0x0841,0x0841,0x0841,0x0841,0x0842,0x0842,0x0842,0x0842
DCW 0x0843,0x0843,0x0843,0x0843,0x0844,0x0844,0x0844,0x0844
DCW 0x0845,0x0845,0x0845,0x0845,0x0846,0x0846,0x0846,0x0847
DCW 0x0847,0x0847,0x0847,0x0848,0x0848,0x0848,0x0848,0x0849
DCW 0x0849,0x0849,0x0849,0x084A,0x084A,0x084A,0x084A,0x084B
DCW 0x084B,0x084B,0x084B,0x084C,0x084C,0x084C,0x084D,0x084D
DCW 0x084D,0x084D,0x084E,0x084E,0x084E,0x084E,0x084F,0x084F
DCW 0x084F,0x0850,0x0850,0x0850,0x0850,0x0851,0x0851,0x0851
DCW 0x0851,0x0852,0x0852,0x0852,0x0853,0x0853,0x0853,0x0853
DCW 0x0854,0x0854,0x0854,0x0854,0x0855,0x0855,0x0855,0x0856
DCW 0x0856,0x0856,0x0856,0x0857,0x0857,0x0857,0x0858,0x0858
DCW 0x0858,0x0858,0x0859,0x0859,0x0859,0x085A,0x085A,0x085A
DCW 0x085A,0x085B,0x085B,0x085B,0x085C,0x085C,0x085C,0x085C
DCW 0x085D,0x085D,0x085D,0x085E,0x085E,0x085E,0x085F,0x085F
DCW 0x085F,0x085F,0x0860,0x0860,0x0860,0x0861,0x0861,0x0861
DCW 0x0861,0x0862,0x0862,0x0862,0x0863,0x0863,0x0863,0x0864
DCW 0x0864,0x0864,0x0864,0x0865,0x0865,0x0865,0x0866,0x0866
DCW 0x0866,0x0867,0x0867,0x0867,0x0868,0x0868,0x0868,0x0868
DCW 0x0869,0x0869,0x0869,0x086A,0x086A,0x086A,0x086B,0x086B
DCW 0x086B,0x086C,0x086C,0x086C,0x086C,0x086D,0x086D,0x086D
DCW 0x086E,0x086E,0x086E,0x086F,0x086F,0x086F,0x0870,0x0870
DCW 0x0870,0x0871,0x0871,0x0871,0x0872,0x0872,0x0872,0x0873
DCW 0x0873,0x0873,0x0874,0x0874,0x0874,0x0874,0x0875,0x0875
DCW 0x0875,0x0876,0x0876,0x0876,0x0877,0x0877,0x0877,0x0878
DCW 0x0878,0x0878,0x0879,0x0879,0x0879,0x087A,0x087A,0x087A
DCW 0x087B,0x087B,0x087B,0x087C,0x087C,0x087C,0x087D,0x087D
DCW 0x087D,0x087E,0x087E,0x087E,0x087F,0x087F,0x087F,0x0880
DCW 0x0880,0x0880,0x0881,0x0881,0x0881,0x0882,0x0882,0x0882
DCW 0x0883,0x0883,0x0883,0x0884,0x0884,0x0885,0x0885,0x0885
DCW 0x0886,0x0886,0x0886,0x0887,0x0887,0x0887,0x0888,0x0888
DCW 0x0888,0x0889,0x0889,0x0889,0x088A,0x088A,0x088A,0x088B
DCW 0x088B,0x088B,0x088C,0x088C,0x088D,0x088D,0x088D,0x088E
DCW 0x088E,0x088E,0x088F,0x088F,0x088F,0x0890,0x0890,0x0890
DCW 0x0891,0x0891,0x0892,0x0892,0x0892,0x0893,0x0893,0x0893
DCW 0x0894,0x0894,0x0894,0x0895,0x0895,0x0895,0x0896,0x0896
DCW 0x0897,0x0897,0x0897,0x0898,0x0898,0x0898,0x0899,0x0899
DCW 0x0899,0x089A,0x089A,0x089B,0x089B,0x089B,0x089C,0x089C
DCW 0x089C,0x089D,0x089D,0x089E,0x089E,0x089E,0x089F,0x089F
DCW 0x089F,0x08A0,0x08A0,0x08A1,0x08A1,0x08A1,0x08A2,0x08A2
DCW 0x08A2,0x08A3,0x08A3,0x08A4,0x08A4,0x08A4,0x08A5,0x08A5
DCW 0x08A5,0x08A6,0x08A6,0x08A7,0x08A7,0x08A7,0x08A8,0x08A8
DCW 0x08A9,0x08A9,0x08A9,0x08AA,0x08AA,0x08AA,0x08AB,0x08AB
DCW 0x08AC,0x08AC,0x08AC,0x08AD,0x08AD,0x08AE,0x08AE,0x08AE
DCW 0x08AF,0x08AF,0x08AF,0x08B0,0x08B0,0x08B1,0x08B1,0x08B1
DCW 0x08B2,0x08B2,0x08B3,0x08B3,0x08B3,0x08B4,0x08B4,0x08B5
DCW 0x08B5,0x08B5,0x08B6,0x08B6,0x08B7,0x08B7,0x08B7,0x08B8
DCW 0x08B8,0x08B9,0x08B9,0x08B9,0x08BA,0x08BA,0x08BB,0x08BB
DCW 0x08BB,0x08BC,0x08BC,0x08BD,0x08BD,0x08BD,0x08BE,0x08BE
DCW 0x08BF,0x08BF,0x08BF,0x08C0,0x08C0,0x08C1,0x08C1,0x08C1
DCW 0x08C2,0x08C2,0x08C3,0x08C3,0x08C3,0x08C4,0x08C4,0x08C5
DCW 0x08C5,0x08C5,0x08C6,0x08C6,0x08C7,0x08C7,0x08C8,0x08C8
DCW 0x08C8,0x08C9,0x08C9,0x08CA,0x08CA,0x08CA,0x08CB,0x08CB
DCW 0x08CC,0x08CC,0x08CD,0x08CD,0x08CD,0x08CE,0x08CE,0x08CF
DCW 0x08CF,0x08CF,0x08D0,0x08D0,0x08D1,0x08D1,0x08D2,0x08D2
DCW 0x08D2,0x08D3,0x08D3,0x08D4,0x08D4,0x08D4,0x08D5,0x08D5
DCW 0x08D6,0x08D6,0x08D7,0x08D7,0x08D7,0x08D8,0x08D8,0x08D9
DCW 0x08D9,0x08DA,0x08DA,0x08DA,0x08DB,0x08DB,0x08DC,0x08DC
DCW 0x08DD,0x08DD,0x08DD,0x08DE,0x08DE,0x08DF,0x08DF,0x08E0
DCW 0x08E0,0x08E0,0x08E1,0x08E1,0x08E2,0x08E2,0x08E3,0x08E3
DCW 0x08E4,0x08E4,0x08E4,0x08E5,0x08E5,0x08E6,0x08E6,0x08E7
DCW 0x08E7,0x08E7,0x08E8,0x08E8,0x08E9,0x08E9,0x08EA,0x08EA
DCW 0x08EB,0x08EB,0x08EB,0x08EC,0x08EC,0x08ED,0x08ED,0x08EE
DCW 0x08EE,0x08EF,0x08EF,0x08EF,0x08F0,0x08F0,0x08F1,0x08F1
DCW 0x08F2,0x08F2,0x08F3,0x08F3,0x08F3,0x08F4,0x08F4,0x08F5
DCW 0x08F5,0x08F6,0x08F6,0x08F7,0x08F7,0x08F8,0x08F8,0x08F8
DCW 0x08F9,0x08F9,0x08FA,0x08FA,0x08FB,0x08FB,0x08FC,0x08FC
DCW 0x08FD,0x08FD,0x08FD,0x08FE,0x08FE,0x08FF,0x08FF,0x0900
DCW 0x0900,0x0901,0x0901,0x0902,0x0902,0x0902,0x0903,0x0903
DCW 0x0904,0x0904,0x0905,0x0905,0x0906,0x0906,0x0907,0x0907
DCW 0x0908,0x0908,0x0908,0x0909,0x0909,0x090A,0x090A,0x090B
DCW 0x090B,0x090C,0x090C,0x090D,0x090D,0x090E,0x090E,0x090F
DCW 0x090F,0x0910,0x0910,0x0910,0x0911,0x0911,0x0912,0x0912
DCW 0x0913,0x0913,0x0914,0x0914,0x0915,0x0915,0x0916,0x0916
DCW 0x0917,0x0917,0x0918,0x0918,0x0918,0x0919,0x0919,0x091A
DCW 0x091A,0x091B,0x091B,0x091C,0x091C,0x091D,0x091D,0x091E
DCW 0x091E,0x091F,0x091F,0x0920,0x0920,0x0921,0x0921,0x0922
DCW 0x0922,0x0923,0x0923,0x0924,0x0924,0x0924,0x0925,0x0925
DCW 0x0926,0x0926,0x0927,0x0927,0x0928,0x0928,0x0929,0x0929
DCW 0x092A,0x092A,0x092B,0x092B,0x092C,0x092C,0x092D,0x092D
DCW 0x092E,0x092E,0x092F,0x092F,0x0930,0x0930,0x0931,0x0931
DCW 0x0932,0x0932,0x0933,0x0933,0x0934,0x0934,0x0935,0x0935
DCW 0x0936,0x0936,0x0937,0x0937,0x0938,0x0938,0x0939,0x0939
DCW 0x093A,0x093A,0x093B,0x093B,0x093C,0x093C,0x093D,0x093D
DCW 0x093E,0x093E,0x093F,0x093F,0x0940,0x0940,0x0941,0x0941
DCW 0x0942,0x0942,0x0943,0x0943,0x0944,0x0944,0x0945,0x0945
DCW 0x0946,0x0946,0x0947,0x0947,0x0948,0x0948,0x0949,0x0949
DCW 0x094A,0x094A,0x094B,0x094B,0x094C,0x094C,0x094D,0x094D
DCW 0x094E,0x094E,0x094F,0x094F,0x0950,0x0950,0x0951,0x0951
DCW 0x0952,0x0952,0x0953,0x0953,0x0954,0x0954,0x0955,0x0956
DCW 0x0956,0x0957,0x0957,0x0958,0x0958,0x0959,0x0959,0x095A
DCW 0x095A,0x095B,0x095B,0x095C,0x095C,0x095D,0x095D,0x095E
DCW 0x095E,0x095F,0x095F,0x0960,0x0960,0x0961,0x0961,0x0962
DCW 0x0962,0x0963,0x0964,0x0964,0x0965,0x0965,0x0966,0x0966
DCW 0x0967,0x0967,0x0968,0x0968,0x0969,0x0969,0x096A,0x096A
DCW 0x096B,0x096B,0x096C,0x096C,0x096D,0x096E,0x096E,0x096F
DCW 0x096F,0x0970,0x0970,0x0971,0x0971,0x0972,0x0972,0x0973
DCW 0x0973,0x0974,0x0974,0x0975,0x0976,0x0976,0x0977,0x0977
DCW 0x0978,0x0978,0x0979,0x0979,0x097A,0x097A,0x097B,0x097B
DCW 0x097C,0x097C,0x097D,0x097E,0x097E,0x097F,0x097F,0x0980
DCW 0x0980,0x0981,0x0981,0x0982,0x0982,0x0983,0x0983,0x0984
DCW 0x0985,0x0985,0x0986,0x0986,0x0987,0x0987,0x0988,0x0988
DCW 0x0989,0x0989,0x098A,0x098B,0x098B,0x098C,0x098C,0x098D
DCW 0x098D,0x098E,0x098E,0x098F,0x098F,0x0990,0x0991,0x0991
DCW 0x0992,0x0992,0x0993,0x0993,0x0994,0x0994,0x0995,0x0996
DCW 0x0996,0x0997,0x0997,0x0998,0x0998,0x0999,0x0999,0x099A
DCW 0x099A,0x099B,0x099C,0x099C,0x099D,0x099D,0x099E,0x099E
DCW 0x099F,0x099F,0x09A0,0x09A1,0x09A1,0x09A2,0x09A2,0x09A3
DCW 0x09A3,0x09A4,0x09A4,0x09A5,0x09A6,0x09A6,0x09A7,0x09A7
DCW 0x09A8,0x09A8,0x09A9,0x09AA,0x09AA,0x09AB,0x09AB,0x09AC
DCW 0x09AC,0x09AD,0x09AD,0x09AE,0x09AF,0x09AF,0x09B0,0x09B0
DCW 0x09B1,0x09B1,0x09B2,0x09B3,0x09B3,0x09B4,0x09B4,0x09B5
DCW 0x09B5,0x09B6,0x09B7,0x09B7,0x09B8,0x09B8,0x09B9,0x09B9
DCW 0x09BA,0x09BA,0x09BB,0x09BC,0x09BC,0x09BD,0x09BD,0x09BE
DCW 0x09BE,0x09BF,0x09C0,0x09C0,0x09C1,0x09C1,0x09C2,0x09C2
DCW 0x09C3,0x09C4,0x09C4,0x09C5,0x09C5,0x09C6,0x09C7,0x09C7
DCW 0x09C8,0x09C8,0x09C9,0x09C9,0x09CA,0x09CB,0x09CB,0x09CC
DCW 0x09CC,0x09CD,0x09CD,0x09CE,0x09CF,0x09CF,0x09D0,0x09D0
DCW 0x09D1,0x09D1,0x09D2,0x09D3,0x09D3,0x09D4,0x09D4,0x09D5
DCW 0x09D6,0x09D6,0x09D7,0x09D7,0x09D8,0x09D8,0x09D9,0x09DA
DCW 0x09DA,0x09DB,0x09DB,0x09DC,0x09DD,0x09DD,0x09DE,0x09DE
DCW 0x09DF,0x09DF,0x09E0,0x09E1,0x09E1,0x09E2,0x09E2,0x09E3
DCW 0x09E4,0x09E4,0x09E5,0x09E5,0x09E6,0x09E7,0x09E7,0x09E8
DCW 0x09E8,0x09E9,0x09E9,0x09EA,0x09EB,0x09EB,0x09EC,0x09EC
DCW 0x09ED,0x09EE,0x09EE,0x09EF,0x09EF,0x09F0,0x09F1,0x09F1
DCW 0x09F2,0x09F2,0x09F3,0x09F4,0x09F4,0x09F5,0x09F5,0x09F6
DCW 0x09F7,0x09F7,0x09F8,0x09F8,0x09F9,0x09FA,0x09FA,0x09FB
DCW 0x09FB,0x09FC,0x09FD,0x09FD,0x09FE,0x09FE,0x09FF,0x09FF
DCW 0x0A00,0x0A01,0x0A01,0x0A02,0x0A03,0x0A03,0x0A04,0x0A04
DCW 0x0A05,0x0A06,0x0A06,0x0A07,0x0A07,0x0A08,0x0A09,0x0A09
DCW 0x0A0A,0x0A0A,0x0A0B,0x0A0C,0x0A0C,0x0A0D,0x0A0D,0x0A0E
DCW 0x0A0F,0x0A0F,0x0A10,0x0A10,0x0A11,0x0A12,0x0A12,0x0A13
DCW 0x0A13,0x0A14,0x0A15,0x0A15,0x0A16,0x0A16,0x0A17,0x0A18
DCW 0x0A18,0x0A19,0x0A1A,0x0A1A,0x0A1B,0x0A1B,0x0A1C,0x0A1D
DCW 0x0A1D,0x0A1E,0x0A1E,0x0A1F,0x0A20,0x0A20,0x0A21,0x0A21
DCW 0x0A22,0x0A23,0x0A23,0x0A24,0x0A25,0x0A25,0x0A26,0x0A26
DCW 0x0A27,0x0A28,0x0A28,0x0A29,0x0A29,0x0A2A,0x0A2B,0x0A2B
DCW 0x0A2C,0x0A2D,0x0A2D,0x0A2E,0x0A2E,0x0A2F,0x0A30,0x0A30
DCW 0x0A31,0x0A32,0x0A32,0x0A33,0x0A33,0x0A34,0x0A35,0x0A35
DCW 0x0A36,0x0A36,0x0A37,0x0A38,0x0A38,0x0A39,0x0A3A,0x0A3A
DCW 0x0A3B,0x0A3B,0x0A3C,0x0A3D,0x0A3D,0x0A3E,0x0A3F,0x0A3F
DCW 0x0A40,0x0A40,0x0A41,0x0A42,0x0A42,0x0A43,0x0A44,0x0A44
DCW 0x0A45,0x0A45,0x0A46,0x0A47,0x0A47,0x0A48,0x0A49,0x0A49
DCW 0x0A4A,0x0A4B,0x0A4B,0x0A4C,0x0A4C,0x0A4D,0x0A4E,0x0A4E
DCW 0x0A4F,0x0A50,0x0A50,0x0A51,0x0A51,0x0A52,0x0A53,0x0A53
DCW 0x0A54,0x0A55,0x0A55,0x0A56,0x0A57,0x0A57,0x0A58,0x0A58
DCW 0x0A59,0x0A5A,0x0A5A,0x0A5B,0x0A5C,0x0A5C,0x0A5D,0x0A5D
DCW 0x0A5E,0x0A5F,0x0A5F,0x0A60,0x0A61,0x0A61,0x0A62,0x0A63
DCW 0x0A63,0x0A64,0x0A64,0x0A65,0x0A66,0x0A66,0x0A67,0x0A68
DCW 0x0A68,0x0A69,0x0A6A,0x0A6A,0x0A6B,0x0A6C,0x0A6C,0x0A6D
DCW 0x0A6D,0x0A6E,0x0A6F,0x0A6F,0x0A70,0x0A71,0x0A71,0x0A72
DCW 0x0A73,0x0A73,0x0A74,0x0A75,0x0A75,0x0A76,0x0A76,0x0A77
DCW 0x0A78,0x0A78,0x0A79,0x0A7A,0x0A7A,0x0A7B,0x0A7C,0x0A7C
DCW 0x0A7D,0x0A7E,0x0A7E,0x0A7F,0x0A80,0x0A80,0x0A81,0x0A81
DCW 0x0A82,0x0A83,0x0A83,0x0A84,0x0A85,0x0A85,0x0A86,0x0A87
DCW 0x0A87,0x0A88,0x0A89,0x0A89,0x0A8A,0x0A8B,0x0A8B,0x0A8C
DCW 0x0A8D,0x0A8D,0x0A8E,0x0A8E,0x0A8F,0x0A90,0x0A90,0x0A91
DCW 0x0A92,0x0A92,0x0A93,0x0A94,0x0A94,0x0A95,0x0A96,0x0A96
DCW 0x0A97,0x0A98,0x0A98,0x0A99,0x0A9A,0x0A9A,0x0A9B,0x0A9C
DCW 0x0A9C,0x0A9D,0x0A9E,0x0A9E,0x0A9F,0x0AA0,0x0AA0,0x0AA1
DCW 0x0AA1,0x0AA2,0x0AA3,0x0AA3,0x0AA4,0x0AA5,0x0AA5,0x0AA6
DCW 0x0AA7,0x0AA7,0x0AA8,0x0AA9,0x0AA9,0x0AAA,0x0AAB,0x0AAB
DCW 0x0AAC,0x0AAD,0x0AAD,0x0AAE,0x0AAF,0x0AAF,0x0AB0,0x0AB1
DCW 0x0AB1,0x0AB2,0x0AB3,0x0AB3,0x0AB4,0x0AB5,0x0AB5,0x0AB6
DCW 0x0AB7,0x0AB7,0x0AB8,0x0AB9,0x0AB9,0x0ABA,0x0ABB,0x0ABB
DCW 0x0ABC,0x0ABD,0x0ABD,0x0ABE,0x0ABF,0x0ABF,0x0AC0,0x0AC1
DCW 0x0AC1,0x0AC2,0x0AC3,0x0AC3,0x0AC4,0x0AC5,0x0AC5,0x0AC6
DCW 0x0AC7,0x0AC7,0x0AC8,0x0AC9,0x0AC9,0x0ACA,0x0ACB,0x0ACB
DCW 0x0ACC,0x0ACD,0x0ACD,0x0ACE,0x0ACF,0x0ACF,0x0AD0,0x0AD1
DCW 0x0AD1,0x0AD2,0x0AD3,0x0AD3,0x0AD4,0x0AD5,0x0AD5,0x0AD6
DCW 0x0AD7,0x0AD8,0x0AD8,0x0AD9,0x0ADA,0x0ADA,0x0ADB,0x0ADC
DCW 0x0ADC,0x0ADD,0x0ADE,0x0ADE,0x0ADF,0x0AE0,0x0AE0,0x0AE1
DCW 0x0AE2,0x0AE2,0x0AE3,0x0AE4,0x0AE4,0x0AE5,0x0AE6,0x0AE6
DCW 0x0AE7,0x0AE8,0x0AE8,0x0AE9,0x0AEA,0x0AEA,0x0AEB,0x0AEC
DCW 0x0AED,0x0AED,0x0AEE,0x0AEF,0x0AEF,0x0AF0,0x0AF1,0x0AF1
DCW 0x0AF2,0x0AF3,0x0AF3,0x0AF4,0x0AF5,0x0AF5,0x0AF6,0x0AF7
DCW 0x0AF7,0x0AF8,0x0AF9,0x0AF9,0x0AFA,0x0AFB,0x0AFC,0x0AFC
DCW 0x0AFD,0x0AFE,0x0AFE,0x0AFF,0x0B00,0x0B00,0x0B01,0x0B02
DCW 0x0B02,0x0B03,0x0B04,0x0B04,0x0B05,0x0B06,0x0B07,0x0B07
DCW 0x0B08,0x0B09,0x0B09,0x0B0A,0x0B0B,0x0B0B,0x0B0C,0x0B0D
DCW 0x0B0D,0x0B0E,0x0B0F,0x0B10,0x0B10,0x0B11,0x0B12,0x0B12
DCW 0x0B13,0x0B14,0x0B14,0x0B15,0x0B16,0x0B16,0x0B17,0x0B18
DCW 0x0B18,0x0B19,0x0B1A,0x0B1B,0x0B1B,0x0B1C,0x0B1D,0x0B1D
DCW 0x0B1E,0x0B1F,0x0B1F,0x0B20,0x0B21,0x0B22,0x0B22,0x0B23
DCW 0x0B24,0x0B24,0x0B25,0x0B26,0x0B26,0x0B27,0x0B28,0x0B28
DCW 0x0B29,0x0B2A,0x0B2B,0x0B2B,0x0B2C,0x0B2D,0x0B2D,0x0B2E
DCW 0x0B2F,0x0B2F,0x0B30,0x0B31,0x0B32,0x0B32,0x0B33,0x0B34
DCW 0x0B34,0x0B35,0x0B36,0x0B36,0x0B37,0x0B38,0x0B39,0x0B39
DCW 0x0B3A,0x0B3B,0x0B3B,0x0B3C,0x0B3D,0x0B3D,0x0B3E,0x0B3F
DCW 0x0B40,0x0B40,0x0B41,0x0B42,0x0B42,0x0B43,0x0B44,0x0B45
DCW 0x0B45,0x0B46,0x0B47,0x0B47,0x0B48,0x0B49,0x0B49,0x0B4A
DCW 0x0B4B,0x0B4C,0x0B4C,0x0B4D,0x0B4E,0x0B4E,0x0B4F,0x0B50
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800,0x0800
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801,0x0801
DCW 0x0801,0x0801,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802
DCW 0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0802
DCW 0x0802,0x0802,0x0802,0x0802,0x0802,0x0802,0x0803,0x0803
DCW 0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803
DCW 0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803,0x0803
DCW 0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804
DCW 0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0804,0x0805
DCW 0x0805,0x0805,0x0805,0x0805,0x0805,0x0805,0x0805,0x0805
DCW 0x0805,0x0805,0x0805,0x0805,0x0806,0x0806,0x0806,0x0806
DCW 0x0806,0x0806,0x0806,0x0806,0x0806,0x0806,0x0806,0x0806
DCW 0x0806,0x0807,0x0807,0x0807,0x0807,0x0807,0x0807,0x0807
DCW 0x0807,0x0807,0x0807,0x0807,0x0807,0x0808,0x0808,0x0808
DCW 0x0808,0x0808,0x0808,0x0808,0x0808,0x0808,0x0808,0x0808
DCW 0x0809,0x0809,0x0809,0x0809,0x0809,0x0809,0x0809,0x0809
DCW 0x0809,0x0809,0x080A,0x080A,0x080A,0x080A,0x080A,0x080A
DCW 0x080A,0x080A,0x080A,0x080A,0x080B,0x080B,0x080B,0x080B
DCW 0x080B,0x080B,0x080B,0x080B,0x080B,0x080B,0x080C,0x080C
DCW 0x080C,0x080C,0x080C,0x080C,0x080C,0x080C,0x080C,0x080D
DCW 0x080D,0x080D,0x080D,0x080D,0x080D,0x080D,0x080D,0x080E
DCW 0x080E,0x080E,0x080E,0x080E,0x080E,0x080E,0x080E,0x080E
DCW 0x080F,0x080F,0x080F,0x080F,0x080F,0x080F,0x080F,0x080F
DCW 0x0810,0x0810,0x0810,0x0810,0x0810,0x0810,0x0810,0x0810
DCW 0x0811,0x0811,0x0811,0x0811,0x0811,0x0811,0x0811,0x0811
DCW 0x0812,0x0812,0x0812,0x0812,0x0812,0x0812,0x0812,0x0813
DCW 0x0813,0x0813,0x0813,0x0813,0x0813,0x0813,0x0814,0x0814
DCW 0x0814,0x0814,0x0814,0x0814,0x0814,0x0814,0x0815,0x0815
DCW 0x0815,0x0815,0x0815,0x0815,0x0816,0x0816,0x0816,0x0816
DCW 0x0816,0x0816,0x0816,0x0817,0x0817,0x0817,0x0817,0x0817
DCW 0x0817,0x0817,0x0818,0x0818,0x0818,0x0818,0x0818,0x0818
DCW 0x0819,0x0819,0x0819,0x0819,0x0819,0x0819,0x0819,0x081A
DCW 0x081A,0x081A,0x081A,0x081A,0x081A,0x081B,0x081B,0x081B
DCW 0x081B,0x081B,0x081B,0x081C,0x081C,0x081C,0x081C,0x081C
DCW 0x081C,0x081D,0x081D,0x081D,0x081D,0x081D,0x081D,0x081E
DCW 0x081E,0x081E,0x081E,0x081E,0x081E,0x081F,0x081F,0x081F
DCW 0x081F,0x081F,0x081F,0x0820,0x0820,0x0820,0x0820,0x0820
DCW 0x0820,0x0821,0x0821,0x0821,0x0821,0x0821,0x0822,0x0822
DCW 0x0822,0x0822,0x0822,0x0822,0x0823,0x0823,0x0823,0x0823
DCW 0x0823,0x0824,0x0824,0x0824,0x0824,0x0824,0x0824,0x0825
DCW 0x0825,0x0825,0x0825,0x0825,0x0826,0x0826,0x0826,0x0826
DCW 0x0826,0x0827,0x0827,0x0827,0x0827,0x0827,0x0828,0x0828
DCW 0x0828,0x0828,0x0828,0x0829,0x0829,0x0829,0x0829,0x0829
DCW 0x082A,0x082A,0x082A,0x082A,0x082A,0x082B,0x082B,0x082B
DCW 0x082B,0x082B,0x082C,0x082C,0x082C,0x082C,0x082C,0x082D
DCW 0x082D,0x082D,0x082D,0x082D,0x082E,0x082E,0x082E,0x082E
DCW 0x082E,0x082F,0x082F,0x082F,0x082F,0x0830,0x0830,0x0830
DCW 0x0830,0x0830,0x0831,0x0831,0x0831,0x0831,0x0831,0x0832
DCW 0x0832,0x0832,0x0832,0x0833,0x0833,0x0833,0x0833,0x0833
DCW 0x0834,0x0834,0x0834,0x0834,0x0835,0x0835,0x0835,0x0835
DCW 0x0835,0x0836,0x0836,0x0836,0x0836,0x0837,0x0837,0x0837
DCW 0x0837,0x0837,0x0838,0x0838,0x0838,0x0838,0x0839,0x0839
DCW 0x0839,0x0839,0x083A,0x083A,0x083A,0x083A,0x083A,0x083B
DCW 0x083B,0x083B,0x083B,0x083C,0x083C,0x083C,0x083C,0x083D
DCW 0x083D,0x083D,0x083D,0x083E,0x083E,0x083E,0x083E,0x083F
DCW 0x083F,0x083F,0x083F,0x0840,0x0840,0x0840,0x0840,0x0840
DCW 0x0841,0x0841,0x0841,0x0841,0x0842,0x0842,0x0842,0x0842
DCW 0x0843,0x0843,0x0843,0x0843,0x0844,0x0844,0x0844,0x0844
DCW 0x0845,0x0845,0x0845,0x0845,0x0846,0x0846,0x0846,0x0847
DCW 0x0847,0x0847,0x0847,0x0848,0x0848,0x0848,0x0848,0x0849
DCW 0x0849,0x0849,0x0849,0x084A,0x084A,0x084A,0x084A,0x084B
DCW 0x084B,0x084B,0x084B,0x084C,0x084C,0x084C,0x084D,0x084D
DCW 0x084D,0x084D,0x084E,0x084E,0x084E,0x084E,0x084F,0x084F
DCW 0x084F,0x0850,0x0850,0x0850,0x0850,0x0851,0x0851,0x0851
DCW 0x0851,0x0852,0x0852,0x0852,0x0853,0x0853,0x0853,0x0853
DCW 0x0854,0x0854,0x0854,0x0854,0x0855,0x0855,0x0855,0x0856
DCW 0x0856,0x0856,0x0856,0x0857,0x0857,0x0857,0x0858,0x0858
DCW 0x0858,0x0858,0x0859,0x0859,0x0859,0x085A,0x085A,0x085A
DCW 0x085A,0x085B,0x085B,0x085B,0x085C,0x085C,0x085C,0x085C
DCW 0x085D,0x085D,0x085D,0x085E,0x085E,0x085E,0x085F,0x085F
DCW 0x085F,0x085F,0x0860,0x0860,0x0860,0x0861,0x0861,0x0861
DCW 0x0861,0x0862,0x0862,0x0862,0x0863,0x0863,0x0863,0x0864
DCW 0x0864,0x0864,0x0864,0x0865,0x0865,0x0865,0x0866,0x0866
DCW 0x0866,0x0867,0x0867,0x0867,0x0868,0x0868,0x0868,0x0868
DCW 0x0869,0x0869,0x0869,0x086A,0x086A,0x086A,0x086B,0x086B
DCW 0x086B,0x086C,0x086C,0x086C,0x086C,0x086D,0x086D,0x086D
DCW 0x086E,0x086E,0x086E,0x086F,0x086F,0x086F,0x0870,0x0870
DCW 0x0870,0x0871,0x0871,0x0871,0x0872,0x0872,0x0872,0x0873
DCW 0x0873,0x0873,0x0874,0x0874,0x0874,0x0874,0x0875,0x0875
DCW 0x0875,0x0876,0x0876,0x0876,0x0877,0x0877,0x0877,0x0878
DCW 0x0878,0x0878,0x0879,0x0879,0x0879,0x087A,0x087A,0x087A
DCW 0x087B,0x087B,0x087B,0x087C,0x087C,0x087C,0x087D,0x087D
DCW 0x087D,0x087E,0x087E,0x087E,0x087F,0x087F,0x087F,0x0880
DCW 0x0880,0x0880,0x0881,0x0881,0x0881,0x0882,0x0882,0x0882
DCW 0x0883,0x0883,0x0883,0x0884,0x0884,0x0885,0x0885,0x0885
DCW 0x0886,0x0886,0x0886,0x0887,0x0887,0x0887,0x0888,0x0888
DCW 0x0888,0x0889,0x0889,0x0889,0x088A,0x088A,0x088A,0x088B
DCW 0x088B,0x088B,0x088C,0x088C,0x088D,0x088D,0x088D,0x088E
DCW 0x088E,0x088E,0x088F,0x088F,0x088F,0x0890,0x0890,0x0890
DCW 0x0891,0x0891,0x0892,0x0892,0x0892,0x0893,0x0893,0x0893
DCW 0x0894,0x0894,0x0894,0x0895,0x0895,0x0895,0x0896,0x0896
DCW 0x0897,0x0897,0x0897,0x0898,0x0898,0x0898,0x0899,0x0899
DCW 0x0899,0x089A,0x089A,0x089B,0x089B,0x089B,0x089C,0x089C
DCW 0x089C,0x089D,0x089D,0x089E,0x089E,0x089E,0x089F,0x089F
DCW 0x089F,0x08A0,0x08A0,0x08A1,0x08A1,0x08A1,0x08A2,0x08A2
DCW 0x08A2,0x08A3,0x08A3,0x08A4,0x08A4,0x08A4,0x08A5,0x08A5
DCW 0x08A5,0x08A6,0x08A6,0x08A7,0x08A7,0x08A7,0x08A8,0x08A8
DCW 0x08A9,0x08A9,0x08A9,0x08AA,0x08AA,0x08AA,0x08AB,0x08AB
DCW 0x08AC,0x08AC,0x08AC,0x08AD,0x08AD,0x08AE,0x08AE,0x08AE
DCW 0x08AF,0x08AF,0x08AF,0x08B0,0x08B0,0x08B1,0x08B1,0x08B1
DCW 0x08B2,0x08B2,0x08B3,0x08B3,0x08B3,0x08B4,0x08B4,0x08B5
DCW 0x08B5,0x08B5,0x08B6,0x08B6,0x08B7,0x08B7,0x08B7,0x08B8
DCW 0x08B8,0x08B9,0x08B9,0x08B9,0x08BA,0x08BA,0x08BB,0x08BB
DCW 0x08BB,0x08BC,0x08BC,0x08BD,0x08BD,0x08BD,0x08BE,0x08BE
DCW 0x08BF,0x08BF,0x08BF,0x08C0,0x08C0,0x08C1,0x08C1,0x08C1
DCW 0x08C2,0x08C2,0x08C3,0x08C3,0x08C3,0x08C4,0x08C4,0x08C5
DCW 0x08C5,0x08C5,0x08C6,0x08C6,0x08C7,0x08C7,0x08C8,0x08C8
DCW 0x08C8,0x08C9,0x08C9,0x08CA,0x08CA,0x08CA,0x08CB,0x08CB
DCW 0x08CC,0x08CC,0x08CD,0x08CD,0x08CD,0x08CE,0x08CE,0x08CF
DCW 0x08CF,0x08CF,0x08D0,0x08D0,0x08D1,0x08D1,0x08D2,0x08D2
DCW 0x08D2,0x08D3,0x08D3,0x08D4,0x08D4,0x08D4,0x08D5,0x08D5
DCW 0x08D6,0x08D6,0x08D7,0x08D7,0x08D7,0x08D8,0x08D8,0x08D9
DCW 0x08D9,0x08DA,0x08DA,0x08DA,0x08DB,0x08DB,0x08DC,0x08DC
DCW 0x08DD,0x08DD,0x08DD,0x08DE,0x08DE,0x08DF,0x08DF,0x08E0
DCW 0x08E0,0x08E0,0x08E1,0x08E1,0x08E2,0x08E2,0x08E3,0x08E3
DCW 0x08E4,0x08E4,0x08E4,0x08E5,0x08E5,0x08E6,0x08E6,0x08E7
DCW 0x08E7,0x08E7,0x08E8,0x08E8,0x08E9,0x08E9,0x08EA,0x08EA
DCW 0x08EB,0x08EB,0x08EB,0x08EC,0x08EC,0x08ED,0x08ED,0x08EE
DCW 0x08EE,0x08EF,0x08EF,0x08EF,0x08F0,0x08F0,0x08F1,0x08F1
DCW 0x08F2,0x08F2,0x08F3,0x08F3,0x08F3,0x08F4,0x08F4,0x08F5
DCW 0x08F5,0x08F6,0x08F6,0x08F7,0x08F7,0x08F8,0x08F8,0x08F8
DCW 0x08F9,0x08F9,0x08FA,0x08FA,0x08FB,0x08FB,0x08FC,0x08FC
DCW 0x08FD,0x08FD,0x08FD,0x08FE,0x08FE,0x08FF,0x08FF,0x0900
DCW 0x0900,0x0901,0x0901,0x0902,0x0902,0x0902,0x0903,0x0903
DCW 0x0904,0x0904,0x0905,0x0905,0x0906,0x0906,0x0907,0x0907
DCW 0x0908,0x0908,0x0908,0x0909,0x0909,0x090A,0x090A,0x090B
DCW 0x090B,0x090C,0x090C,0x090D,0x090D,0x090E,0x090E,0x090F
DCW 0x090F,0x0910,0x0910,0x0910,0x0911,0x0911,0x0912,0x0912
DCW 0x0913,0x0913,0x0914,0x0914,0x0915,0x0915,0x0916,0x0916
DCW 0x0917,0x0917,0x0918,0x0918,0x0918,0x0919,0x0919,0x091A
DCW 0x091A,0x091B,0x091B,0x091C,0x091C,0x091D,0x091D,0x091E
DCW 0x091E,0x091F,0x091F,0x0920,0x0920,0x0921,0x0921,0x0922
DCW 0x0922,0x0923,0x0923,0x0924,0x0924,0x0924,0x0925,0x0925
DCW 0x0926,0x0926,0x0927,0x0927,0x0928,0x0928,0x0929,0x0929
DCW 0x092A,0x092A,0x092B,0x092B,0x092C,0x092C,0x092D,0x092D
DCW 0x092E,0x092E,0x092F,0x092F,0x0930,0x0930,0x0931,0x0931
DCW 0x0932,0x0932,0x0933,0x0933,0x0934,0x0934,0x0935,0x0935
DCW 0x0936,0x0936,0x0937,0x0937,0x0938,0x0938,0x0939,0x0939
DCW 0x093A,0x093A,0x093B,0x093B,0x093C,0x093C,0x093D,0x093D
DCW 0x093E,0x093E,0x093F,0x093F,0x0940,0x0940,0x0941,0x0941
DCW 0x0942,0x0942,0x0943,0x0943,0x0944,0x0944,0x0945,0x0945
DCW 0x0946,0x0946,0x0947,0x0947,0x0948,0x0948,0x0949,0x0949
DCW 0x094A,0x094A,0x094B,0x094B,0x094C,0x094C,0x094D,0x094D
DCW 0x094E,0x094E,0x094F,0x094F,0x0950,0x0950,0x0951,0x0951
DCW 0x0952,0x0952,0x0953,0x0953,0x0954,0x0954,0x0955,0x0956
DCW 0x0956,0x0957,0x0957,0x0958,0x0958,0x0959,0x0959,0x095A
DCW 0x095A,0x095B,0x095B,0x095C,0x095C,0x095D,0x095D,0x095E
DCW 0x095E,0x095F,0x095F,0x0960,0x0960,0x0961,0x0961,0x0962
DCW 0x0962,0x0963,0x0964,0x0964,0x0965,0x0965,0x0966,0x0966
DCW 0x0967,0x0967,0x0968,0x0968,0x0969,0x0969,0x096A,0x096A
DCW 0x096B,0x096B,0x096C,0x096C,0x096D,0x096E,0x096E,0x096F
DCW 0x096F,0x0970,0x0970,0x0971,0x0971,0x0972,0x0972,0x0973
DCW 0x0973,0x0974,0x0974,0x0975,0x0976,0x0976,0x0977,0x0977
DCW 0x0978,0x0978,0x0979,0x0979,0x097A,0x097A,0x097B,0x097B
DCW 0x097C,0x097C,0x097D,0x097E,0x097E,0x097F,0x097F,0x0980
DCW 0x0980,0x0981,0x0981,0x0982,0x0982,0x0983,0x0983,0x0984
DCW 0x0985,0x0985,0x0986,0x0986,0x0987,0x0987,0x0988,0x0988
DCW 0x0989,0x0989,0x098A,0x098B,0x098B,0x098C,0x098C,0x098D
DCW 0x098D,0x098E,0x098E,0x098F,0x098F,0x0990,0x0991,0x0991
DCW 0x0992,0x0992,0x0993,0x0993,0x0994,0x0994,0x0995,0x0996
DCW 0x0996,0x0997,0x0997,0x0998,0x0998,0x0999,0x0999,0x099A
DCW 0x099A,0x099B,0x099C,0x099C,0x099D,0x099D,0x099E,0x099E
DCW 0x099F,0x099F,0x09A0,0x09A1,0x09A1,0x09A2,0x09A2,0x09A3
DCW 0x09A3,0x09A4,0x09A4,0x09A5,0x09A6,0x09A6,0x09A7,0x09A7
DCW 0x09A8,0x09A8,0x09A9,0x09AA,0x09AA,0x09AB,0x09AB,0x09AC
DCW 0x09AC,0x09AD,0x09AD,0x09AE,0x09AF,0x09AF,0x09B0,0x09B0
DCW 0x09B1,0x09B1,0x09B2,0x09B3,0x09B3,0x09B4,0x09B4,0x09B5
DCW 0x09B5,0x09B6,0x09B7,0x09B7,0x09B8,0x09B8,0x09B9,0x09B9
DCW 0x09BA,0x09BA,0x09BB,0x09BC,0x09BC,0x09BD,0x09BD,0x09BE
DCW 0x09BE,0x09BF,0x09C0,0x09C0,0x09C1,0x09C1,0x09C2,0x09C2
DCW 0x09C3,0x09C4,0x09C4,0x09C5,0x09C5,0x09C6,0x09C7,0x09C7
DCW 0x09C8,0x09C8,0x09C9,0x09C9,0x09CA,0x09CB,0x09CB,0x09CC
DCW 0x09CC,0x09CD,0x09CD,0x09CE,0x09CF,0x09CF,0x09D0,0x09D0
DCW 0x09D1,0x09D1,0x09D2,0x09D3,0x09D3,0x09D4,0x09D4,0x09D5
DCW 0x09D6,0x09D6,0x09D7,0x09D7,0x09D8,0x09D8,0x09D9,0x09DA
DCW 0x09DA,0x09DB,0x09DB,0x09DC,0x09DD,0x09DD,0x09DE,0x09DE
DCW 0x09DF,0x09DF,0x09E0,0x09E1,0x09E1,0x09E2,0x09E2,0x09E3
DCW 0x09E4,0x09E4,0x09E5,0x09E5,0x09E6,0x09E7,0x09E7,0x09E8
DCW 0x09E8,0x09E9,0x09E9,0x09EA,0x09EB,0x09EB,0x09EC,0x09EC
DCW 0x09ED,0x09EE,0x09EE,0x09EF,0x09EF,0x09F0,0x09F1,0x09F1
DCW 0x09F2,0x09F2,0x09F3,0x09F4,0x09F4,0x09F5,0x09F5,0x09F6
DCW 0x09F7,0x09F7,0x09F8,0x09F8,0x09F9,0x09FA,0x09FA,0x09FB
DCW 0x09FB,0x09FC,0x09FD,0x09FD,0x09FE,0x09FE,0x09FF,0x09FF
DCW 0x0A00,0x0A01,0x0A01,0x0A02,0x0A03,0x0A03,0x0A04,0x0A04
DCW 0x0A05,0x0A06,0x0A06,0x0A07,0x0A07,0x0A08,0x0A09,0x0A09
DCW 0x0A0A,0x0A0A,0x0A0B,0x0A0C,0x0A0C,0x0A0D,0x0A0D,0x0A0E
DCW 0x0A0F,0x0A0F,0x0A10,0x0A10,0x0A11,0x0A12,0x0A12,0x0A13
DCW 0x0A13,0x0A14,0x0A15,0x0A15,0x0A16,0x0A16,0x0A17,0x0A18
DCW 0x0A18,0x0A19,0x0A1A,0x0A1A,0x0A1B,0x0A1B,0x0A1C,0x0A1D
DCW 0x0A1D,0x0A1E,0x0A1E,0x0A1F,0x0A20,0x0A20,0x0A21,0x0A21
DCW 0x0A22,0x0A23,0x0A23,0x0A24,0x0A25,0x0A25,0x0A26,0x0A26
DCW 0x0A27,0x0A28,0x0A28,0x0A29,0x0A29,0x0A2A,0x0A2B,0x0A2B
DCW 0x0A2C,0x0A2D,0x0A2D,0x0A2E,0x0A2E,0x0A2F,0x0A30,0x0A30
DCW 0x0A31,0x0A32,0x0A32,0x0A33,0x0A33,0x0A34,0x0A35,0x0A35
DCW 0x0A36,0x0A36,0x0A37,0x0A38,0x0A38,0x0A39,0x0A3A,0x0A3A
DCW 0x0A3B,0x0A3B,0x0A3C,0x0A3D,0x0A3D,0x0A3E,0x0A3F,0x0A3F
DCW 0x0A40,0x0A40,0x0A41,0x0A42,0x0A42,0x0A43,0x0A44,0x0A44
DCW 0x0A45,0x0A45,0x0A46,0x0A47,0x0A47,0x0A48,0x0A49,0x0A49
DCW 0x0A4A,0x0A4B,0x0A4B,0x0A4C,0x0A4C,0x0A4D,0x0A4E,0x0A4E
DCW 0x0A4F,0x0A50,0x0A50,0x0A51,0x0A51,0x0A52,0x0A53,0x0A53
DCW 0x0A54,0x0A55,0x0A55,0x0A56,0x0A57,0x0A57,0x0A58,0x0A58
DCW 0x0A59,0x0A5A,0x0A5A,0x0A5B,0x0A5C,0x0A5C,0x0A5D,0x0A5D
DCW 0x0A5E,0x0A5F,0x0A5F,0x0A60,0x0A61,0x0A61,0x0A62,0x0A63
DCW 0x0A63,0x0A64,0x0A64,0x0A65,0x0A66,0x0A66,0x0A67,0x0A68
DCW 0x0A68,0x0A69,0x0A6A,0x0A6A,0x0A6B,0x0A6C,0x0A6C,0x0A6D
DCW 0x0A6D,0x0A6E,0x0A6F,0x0A6F,0x0A70,0x0A71,0x0A71,0x0A72
DCW 0x0A73,0x0A73,0x0A74,0x0A75,0x0A75,0x0A76,0x0A76,0x0A77
DCW 0x0A78,0x0A78,0x0A79,0x0A7A,0x0A7A,0x0A7B,0x0A7C,0x0A7C
DCW 0x0A7D,0x0A7E,0x0A7E,0x0A7F,0x0A80,0x0A80,0x0A81,0x0A81
DCW 0x0A82,0x0A83,0x0A83,0x0A84,0x0A85,0x0A85,0x0A86,0x0A87
DCW 0x0A87,0x0A88,0x0A89,0x0A89,0x0A8A,0x0A8B,0x0A8B,0x0A8C
DCW 0x0A8D,0x0A8D,0x0A8E,0x0A8E,0x0A8F,0x0A90,0x0A90,0x0A91
DCW 0x0A92,0x0A92,0x0A93,0x0A94,0x0A94,0x0A95,0x0A96,0x0A96
DCW 0x0A97,0x0A98,0x0A98,0x0A99,0x0A9A,0x0A9A,0x0A9B,0x0A9C
DCW 0x0A9C,0x0A9D,0x0A9E,0x0A9E,0x0A9F,0x0AA0,0x0AA0,0x0AA1
DCW 0x0AA1,0x0AA2,0x0AA3,0x0AA3,0x0AA4,0x0AA5,0x0AA5,0x0AA6
DCW 0x0AA7,0x0AA7,0x0AA8,0x0AA9,0x0AA9,0x0AAA,0x0AAB,0x0AAB
DCW 0x0AAC,0x0AAD,0x0AAD,0x0AAE,0x0AAF,0x0AAF,0x0AB0,0x0AB1
DCW 0x0AB1,0x0AB2,0x0AB3,0x0AB3,0x0AB4,0x0AB5,0x0AB5,0x0AB6
DCW 0x0AB7,0x0AB7,0x0AB8,0x0AB9,0x0AB9,0x0ABA,0x0ABB,0x0ABB
DCW 0x0ABC,0x0ABD,0x0ABD,0x0ABE,0x0ABF,0x0ABF,0x0AC0,0x0AC1
DCW 0x0AC1,0x0AC2,0x0AC3,0x0AC3,0x0AC4,0x0AC5,0x0AC5,0x0AC6
DCW 0x0AC7,0x0AC7,0x0AC8,0x0AC9,0x0AC9,0x0ACA,0x0ACB,0x0ACB
DCW 0x0ACC,0x0ACD,0x0ACD,0x0ACE,0x0ACF,0x0ACF,0x0AD0,0x0AD1
DCW 0x0AD1,0x0AD2,0x0AD3,0x0AD3,0x0AD4,0x0AD5,0x0AD5,0x0AD6
DCW 0x0AD7,0x0AD8,0x0AD8,0x0AD9,0x0ADA,0x0ADA,0x0ADB,0x0ADC
DCW 0x0ADC,0x0ADD,0x0ADE,0x0ADE,0x0ADF,0x0AE0,0x0AE0,0x0AE1
DCW 0x0AE2,0x0AE2,0x0AE3,0x0AE4,0x0AE4,0x0AE5,0x0AE6,0x0AE6
DCW 0x0AE7,0x0AE8,0x0AE8,0x0AE9,0x0AEA,0x0AEA,0x0AEB,0x0AEC
DCW 0x0AED,0x0AED,0x0AEE,0x0AEF,0x0AEF,0x0AF0,0x0AF1,0x0AF1
DCW 0x0AF2,0x0AF3,0x0AF3,0x0AF4,0x0AF5,0x0AF5,0x0AF6,0x0AF7
DCW 0x0AF7,0x0AF8,0x0AF9,0x0AF9,0x0AFA,0x0AFB,0x0AFC,0x0AFC
DCW 0x0AFD,0x0AFE,0x0AFE,0x0AFF,0x0B00,0x0B00,0x0B01,0x0B02
DCW 0x0B02,0x0B03,0x0B04,0x0B04,0x0B05,0x0B06,0x0B07,0x0B07
DCW 0x0B08,0x0B09,0x0B09,0x0B0A,0x0B0B,0x0B0B,0x0B0C,0x0B0D
DCW 0x0B0D,0x0B0E,0x0B0F,0x0B10,0x0B10,0x0B11,0x0B12,0x0B12
DCW 0x0B13,0x0B14,0x0B14,0x0B15,0x0B16,0x0B16,0x0B17,0x0B18
DCW 0x0B18,0x0B19,0x0B1A,0x0B1B,0x0B1B,0x0B1C,0x0B1D,0x0B1D
DCW 0x0B1E,0x0B1F,0x0B1F,0x0B20,0x0B21,0x0B22,0x0B22,0x0B23
DCW 0x0B24,0x0B24,0x0B25,0x0B26,0x0B26,0x0B27,0x0B28,0x0B28
DCW 0x0B29,0x0B2A,0x0B2B,0x0B2B,0x0B2C,0x0B2D,0x0B2D,0x0B2E
DCW 0x0B2F,0x0B2F,0x0B30,0x0B31,0x0B32,0x0B32,0x0B33,0x0B34
DCW 0x0B34,0x0B35,0x0B36,0x0B36,0x0B37,0x0B38,0x0B39,0x0B39
DCW 0x0B3A,0x0B3B,0x0B3B,0x0B3C,0x0B3D,0x0B3D,0x0B3E,0x0B3F
DCW 0x0B40,0x0B40,0x0B41,0x0B42,0x0B42,0x0B43,0x0B44,0x0B45
DCW 0x0B45,0x0B46,0x0B47,0x0B47,0x0B48,0x0B49,0x0B49,0x0B4A
DCW 0x0B4B,0x0B4C,0x0B4C,0x0B4D,0x0B4E,0x0B4E,0x0B4F,0x0B50
Младшее значение 0x800h, что означает 2048. Cтаршее 0xB50, и оно означает 2896.
2896/2048 = 1.414, что соответствует 1/cos(45).
Для получения индекса массива необходимо умножить Y на 2048 и разделить на Х.
Полученный индекс укажет на ячейку массива, из этой ячейки извлекаем значение, умножаем X на него и делим на 2048. Полученный результат есть длина вектора.
Хочу заметить, что деление и умножение на 2048 выполняется сдвигом, и еще одно деление и умножение выполняется специальными командами или алгоритмами, если в используемой платформе нет команд умножения и/или деления.
В моем случае применялся микроконтроллер STM32F103, который имел команды деления и умножения.
Подведем итог алгоритма.
- Проверка знака по Y и разворот, если необходимо.
- Проверка знака по X и разворот, если необходимо.
- Сравнение X и Y и обмен местами, если необходимо.
- Проверка X на 0.
- Умножение Y на 2048 сдвигом.
- Деление Y на X.
- Прибавляем полученное значение к адресу массива и читаем значение K.
- Умножаем X на K.
- Делим X на 2048 сдвигом.
Получившаяся программа на языке ассемблер для STM32F103.
Программа
;r5 - X
;r6 - Y
Magnitude
mov32 r2,0x7FF
mov32 r3,0x7FF
cmp r5,r2
blo Magnitude_xdn
Magnitude_xup
sub r5,r2
b Magnitude_X
Magnitude_xdn
sub r2,r5
mov r5,r2
Magnitude_X ;X in r5
cmp r6,r3
blo Magnitude_ydn
Magnitude_yup
sub r6,r3
b Magnitude_Y
Magnitude_ydn
sub r3,r6
mov r6,r3
Magnitude_Y ;Y in r6
cmp r5,r6
blo Magnitude_neg
Magnitude_pos
mov r1,r5
mov r5,r6
mov r6,r1
Magnitude_neg ;Rotating 45 degree
cbz r6,Magnitude_Zero
lsl r5,#0xC
udiv r5,r6
mov32 r2,#0xFFFFFFFE
and r5,r2
mov32 r2,Magnitude_Table
add r2,r5
ldrh r0,[r2]
mul r6,r0
lsr r6,#0xB
Magnitude_Zero
pop {lr}
bx lr
;In r6 length of vector
Приведу пример работы алгоритма в сравнении с классическим методом для двух из четырех векторов, которые показаны на изображениях выше.
Возьмем синий вектор (из третьей области).
Его координаты X=-45,Y=-126 (можно проверить по пикселям)
Классический метод:
(-45)^2+(-126)^2=2025+15876=17901
SQRT(17901)=133 (усечено до целого)
Алгоритм:
X=2047-45=2002, Y=2047-126=1921
пункт 1: 2002>2047? -> нет. X=2047-2002=45
пункт 2: 1921>2047? -> нет. Y=2047-1921=126
пункт 3: 126>45 -> да. меняем местами X=126, Y=45
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=45*2048=92160
пункт 6: I=Y/X, I=92160/126=731
Пункт 7: в таблице 255 строк по 8 значений, ищем 731е значение.
Это 91я строка и 3е значение, которое равно 0x087e, или 2174 в десятичном
виде.
Пункт 8: X=X*2174, X=126*2174=273924
Пункт 9: A=X/2048, A=273924/2048=133 (усечено до целого)
Ч.Т.Д.
Теперь возьмем зеленый вектор (из четвертой области).
Его координаты X=-170,Y=95 (можно проверить по пикселям).
Классический метод:
(-170)^2+(95)^2=28900+9025=37925
SQRT(37925)=194 (усечено до целого)
Алгоритм:
X=2047-170=1877, Y=2047+95=2142
пункт 1: 1877>2047? -> нет. X=2047-1877=170
пункт 2: 2142>2047? -> да. Y=2142-2047=95
пункт 3: 95>170 -> нет. оставляем как есть.
пункт 4: X=0 -> нет. продолжаем
пункт 5: Y=Y*2048, Y=95*2048=194560
пункт 6: I=Y/X, I=194560/170=1144
Пункт 7: в таблице ищем 1144е значение.
Это 143я строка и 0е значение, которое равно 0x092A, или 2346 в десятичном виде.
Пункт 8: X=X*2346, X=170*2346=398820
Пункт 9: A=X/2048, A=398820/2048=194 (усечено до целого)
Ч.Т.Д.
Итог
Подобный алгоритм можно использовать в ЦОС (как я), например, можно заметно ускорить Быстрое Преобразование Фурье. Также можно использовать в компьютерной графике, где используется трассировка лучей. Возможно и еще есть применение.
На этом все. Спасибо за внимание.
nerudo
Вы сами изобрели CORDIC или просто попытались изложить его для непосвященного слушателя?
PS Если не гнаться за точностью, то есть элементарный Alpha max plus beta min algorithm.
ZEvS_Poisk Автор
Изобрел сам. Ну и в публикации об этом есть. Ну и реализацию выложил, хотя уже еще ее оптимизировал.
ZEvS_Poisk Автор
UPD: Изобретением я считаю «выворот вокруг оси 45 градусов», это уменьшает LUT вдвое.
sshikov
Ну, строго говоряя, этому изобретению тоже сто лет в обед. Синус всегда так считали, например. Т.е. аргумент приводится к некоторому стандартному диапазону, а потом по таблице. И вполне обычный размен потребления памяти на быстродействие.
BigBeaver
А еще синус малых углов численно равен углу до нескольких знаков. Если разрядность низкая, то половину таблицы можно выбросить.
sshikov
Ну да. Я в общем клоню к тому, что когда я начинал, то типовая машина М-222 была примерно такой, какие сегодня микропроцессоры (16 килослов или примерно 48 современных килобайт, например). Так что подобные методы применялись еще тогда и весьма широко. Тогда — это примерно 70-е, то есть лет 50 тому.
ZEvS_Poisk Автор
Да, я провел много тестов с таблицами, и пришел к простому империческому правилу. Количество элементов в таблице должно быть равно количеству значений Х или Y. То есть, имеем 11-битное значение X, тогда в таблице 2^11 значений. Если входные данные вектора, например, 256 значений — 8-битные, то в таблице 256 элементов.
Это верно для соответствия 1:1 при расчете классическим «пифагоровым» методом.
При меньших таблицах — да тоже работает, но точность в некоторых значениях начинает убывать.
BigBeaver
Ну если вам хватает памяти, то как бы и пофиг. Но думаю, что при 8-битной точности таки можно выкинуть нижнюю треть без заметных потерь.
ladle
Извините, функция Ctrl/Enter (чтобы послать сообщение об опечатке лично автору) в комментариях не работает.
ZEvS_Poisk Автор
Ок, учту. Правка комментария тоже не работает. Спустя положенное время.
ZEvS_Poisk Автор
Я не на что не претендую. Вы, слишком прямо ко всему отнеслись. Я описал свой опыт, который выглядит как история, под названием «как я отказался...».
Под изобретением я имею ввиду не что-то фундаментальное, но способность собрать новый дом из старых кирпичей.
Например, человек, который придумал автомагнитолу, всего-лишь придумал, как вставить радио в автомобиль, хотя и радио и автомобиль изобрели до него. И он — изобретатель. А есть человек, который придумал прикрепить ластик на обратную сторону карандаша, и это тоже изобретение.
sshikov
>Я не на что не претендую.
А я не говорил, что что-то изобрести повторно — это плохо. Нормальная статья, я это написал вовсе не ради того, чтобы покритиковать.
ZEvS_Poisk Автор
Ну, тогда спасибо на добром слове!
Gryphon88
Про такие вещи рассказывают на какой дисциплине? Вычмат?
nerudo
Это все относится к прикладным задачам Цифровой Обработки Сигналов (ЦОС, DSP), но вот как может в наше забюрократизированное время это называться в учебных заведениях — даже не знаю. Вычмат вряд ли, там все-таки более академично все и проблема вычисления квадратного корня обычно не стоит…
BigBeaver
У нас на ЦОС было. Вроде.