11.05.2020 14:34
dima_borisenkov 17 3100 Источник
image

В индустрии существует целый ряд кейсов, требующих распознавания номера по фотографии
(scene number recognition). Часто требуемым условием для алгоритма распознавания является низкое значение ошибки второго рода, а именно случаи, когда распознается неверный номер. В качестве примера таких задач можно привести:


  1. Распознавание номера на скидочных, банковских картах, рисунок 1.
  2. Распознавание номера автомобиля, рисунок 2.

image

Рисунок 1 – Карта лояльности
Рисунок 2 – Изображение, содержащее регистрационный номер в низком качестве


Среди проблем, связанных с распознаванием номера, можно выделить:


  • Большое разнообразие шрифтов;
  • Отсутствие зависимости между предыдущими и последующими символами номера (в отличие от задачи распознавания текста);
  • Высокий уровень шумов по причине того, что съемка ведется в различных условиях освещенности, с разного оборудования и т.д.

Задача


Разработать алгоритм распознавания номера на изображении (scene number recognition) при обязательном условии: ошибка второго рода должна быть не больше 0.03.


ошибка второго рода

false positive (FP) — случаи, когда мы приняли за правду ошибочный результат. К примеру, когда реальный номер "177", а алгоритм распознал его как "777", после чего мы приняли результат за истину.


Решение


Разработанный сервис представляет собой композицию двух моделей, основанных на алгоритме CRNN (Convolutional Reccurent Neural Network)[1].


Проект обучения каждой из моделей можно найти в моем репозитории на github.


Проект реализован на Python3, с помощью библиотеки PyTorch.


Детекция областей с номером производилась отдельно обученной сетью для сегментации PSPNet[2]. В скором времени, я планирую выложить на github свою реализацию PSPNet на Pytorch.


Теоретические основы работы


В данном разделе кратко рассмотрим архитектуру алгоритма CRNN, для более подробного
изучения можно прочитать статьи на medium [3], [4].


Структурная схема алгоритма CRNN представлена на рисунке 3.


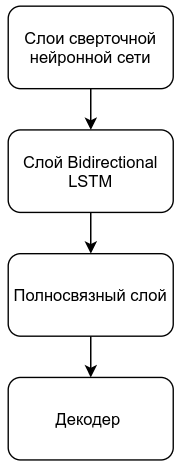
image

Рисунок 3 – Структурная схема алгоритма CRNN


Кратко рассмотрим каждый из этапов поиска номера. Для более глубокого понимания, можно обратиться к источникам: CNN [5], LSTM [6].


Этапы поиска номера:


  1. Процесс формирования матрицы признаков при помощи CNN. Сверточная нейронная сеть состоит из определенного количества сверточных слоев. От первого к последнему слою происходит выделение все более высокоуровневых признаков, при этом, в данном случае, высота карт признаков уменьшается до единицы, что позволяет получить двумерную выходную матрицу признаков. В сформированной матрице каждый столбец представляет собой вектор признаков, обладающий ограниченным рецептивным полем входного изображения. Кроме того, положение вектора признаков соответствует положению рецептивного поля на исходном изображении, рисунок 4;
  2. Использование рекуррентной нейронной сети LSTM. В сети LSTM каждый вектор признаков представляет собой один временной отсчет (time step). LSTM используется для обучения зависимостям между различными отсчетами временной последовательности. В данном случае LSTM используется в режиме many to many, то есть длины входной и выходной временной последовательности одинаковы. Однако, так как в алгоритме используется Bidirectional LSTM, размерность выходного вектора признаков для каждого временного отсчета в два раза больше размерности входного вектора;
  3. Использование полносвязного слоя. В данном алгоритме первый полносвязный слой используется для задачи понижения размерности и выделения признаков. Второй полносвязный слой — для решения задачи классификации;
  4. Декодирование матрицы признаков в вектор символов. В процессе декодирования для каждой позиции n истинный номер класса получается как индекс максимального элемента вектора Yn: kn = max(Yn). Далее каждый номер класса декодируется соответствующим символом, таким образом, формируется вектор предсказанных символов. Далее повторяющиеся элементы объединяются, к примеру, для номера может быть получен следующий результат: «3200-544». Символ "-" служебный, обозначает переход между символами. Если его нет и символы одинаковые, как в нашем случае «00» и «44», декодируем их как один символ.

image

Рисунок 4 – Слои сверточной нейронной сети
где: h, w — высота и ширина карты признаков; n — количество карт признаков для текущего слоя.


Понижение ошибки второго рода


Предположим, имеется сильно зашумленное изображение, рисунок 5.


image

Рисунок 5? – ?Изображение с сильной деградацией

В таком случае сеть тоже предскажет номер, однако для некоторых позиций ее предсказание будет неопределенным: на случайное входное воздействие будет получен случайный результат.


Это условие можно использовать для уменьшения ошибки распознавания.


Рассмотрим композицию двух моделей CRNN работающих параллельно, рисунок 6.


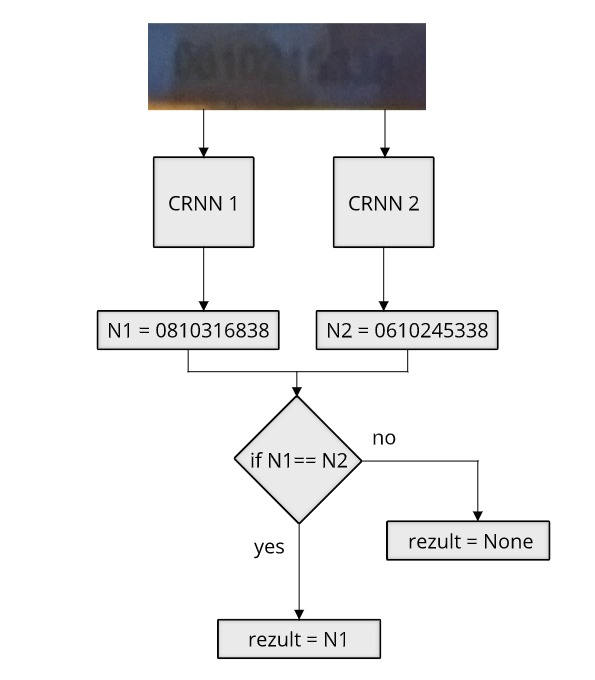
image

Рисунок? 6 – Композиция моделей. Обе модели предсказывают результат: если он одинаков, то возвращается номер, в противном случае пустое значение. CRNN 1, CRNN 2 — первая и вторая модели предсказания номера


Основным моментом, позволяющим моделям успешно распознавать номера и не ошибаться одинаковым образом, является их различная архитектура и процесс обучения. Данные отличия позволяют моделям с высокой вероятностью по-разному реагировать на одни и те же случайные воздействия.


Объяснение помехоустойчивости моделей основано на теории вероятности.

Предположим, нам необходимо распознать номер содержащий один символ "5" на сильно размытом изображении, где невозможно прочитать этот символ. В таком случае помеха, носящая случайных характер, превосходит сигнал. Будем считать помеху аддитивной, тогда:


$x = s + v, v>x$
где: s — сигнал, v — помеха, x — входное воздействие.


В таком случае ответ сети на случайное воздействие также будет случайным. Будем считать, что функция сети от случайного входа описывается равномерным законом распределения:


$y = f(x), y \sim U$
где: f — решающая функция сети, x — входное воздействие, y — выходное значение.


В таком случае для 10 классов вероятность ошибочного предсказания pf = 0.9.


В случае использования композиции моделей вероятность ошибочного предсказания:


pf = $\sum\limits_{i=1, j=1}^{10}P(y = y_j\, |\, y_i=y_j)$
где: pf — вероятность ошибочного предсказания, $y_i$ — предсказание первой модели i-го класса, $y_j$ — предсказание второй модели j-го класса.


В случае 10 классов, для композиции моделей pf = 0.1, вместо pf = 0.9 для одной модели.
При этом, если вероятность верного предсказания символа при низком значении помехи ps = 0.97, тогда вероятность верного предсказания символа композицией: pk = 0.97*0.97 = 0.94.


Различия в моделях появляются уже по естественным причинам: ввиду инициализации случайных весов перед обучением и перемешиванием датасета в процессе обучения.
Также, для того чтобы еще немного изменить процесс обучения, можно изменить размер входного изображения. К примеру, при обучении первой модели приводить размер входного изображения к S = (280, 64), второй модели к S2 = (320, 64).


Приведем архитектуру, которую я использовал для построения композиции моделей. Будем считать размер входного изображения S = (280, 64), таблица 1.


image

Таблица 1 – Архитектура модели.
где: BS — размер батча; AS — длина алфавита; k, s, p — размер ядра, смещение, паддинг соответственно, для обоих операций: свертки и max_pooling


Результаты


Приведем результаты обучения композиции моделей по распознаванию номера. Как было сказано ранее, модель обучалась на заранее обрезанных областях с номером. Область с номером была найдена при помощи модели сегментации PSPNet.


Обучение проводилось на 400 тысячах изображений карт лояльности, валидация — на 100 тысячах, при этом значения номеров вводились владельцами карт, таким образом, 5-10 % карт может быть размеченными, при этом номера могут быть нечитаемыми, рисунок 5.



Таблица 2 – Результаты тестирования композиции моделей. inter_bad — ошиблись обе модели, inter_good — правильно предсказали обе модели; good_1, good_2 — правильно предсказала первая, вторая модель соответственно; amount_cards — общее количество карт, percent_good_1, percent_good_2 — процент верных предсказаний первой, второй модели соответственно; percent_good — процент пересечений верных предсказаний; percent_bad — процент пересечений ложных предсказаний

Если использовать только одну модель, к примеру, модель 1, точность составит 0.8816, при этом ошибка составит 0.1184. В данном случае нет разделения на ошибку первого и второго рода, так как модель во всех случаях предсказывает какой-либо результат.


Если использовать композицию моделей, в таком случае точность понижается на 0.0177, становится 0.863813, при этом ошибка понижается на 0.0954 и становится 0.0230. Таким образом, использование композиции моделей позволило значительно сократить ошибку с небольшим уменьшением точности.


Примеры распознавания номера


Случаи верного распознавания номера алгоритмом


Зеленым цветом обозначены верные предсказания

Случаи ошибочного распознавания номера алгоритмом


Красным цветом обозначены ошибочные предсказания, зеленым — эталонные значения

Случаи, когда алгоритм верно распознал номер, при этом эталонное значение было неверным


Зеленым цветом обозначены верные предсказания

Анализ результатов


В процессе анализа ошибок были выделены три основные причины их появления:


  • Пропуск нечисловых символов. Модель не смогла обобщиться на символы латиницы, так как их процент был очень мал в обучающей выборке. Для устранения этой проблемы необходимо формировать датасет более сбалансированным, возможно, за счет синтезированных данных;
  • Неверные эталонные значения. Примерно в половине ошибочных предсказаний алгоритм предсказывал верное значение, а эталонное было ложным;
  • Ошибки сегментации. В малом проценте случаев часть номера не была сегментирована.

Заключение


По моему мнению, алгоритм CRNN применим для решения ряда прикладных задач scene text recognition, ввиду высокой точности и низких требований к вычислительным ресурсам.
В случае построения композиции моделей на основе CRNN, становится возможным решать задачи, требующие низкого процента ошибки второго рода.


Кроме данного подхода я пробовал отсекать ложные предсказания с вероятностью меньше некоторого порога, однако, в данном случае точность предсказания падала до 0.3, что было неприемлемо.


Список источников


  1. Оригинальная статья CRNN;
  2. Pyramid Scene Parsing Network
  3. Build a Handwritten Text Recognition System using TensorFlow;
  4. An Intuitive Explanation of Connectionist Temporal Classification;
  5. Сверточная нейронная сеть на python
  6. LSTM – сети долгой краткосрочной памяти