Словесные доказательства с трудом даются тем, кто привык мыслить визуально. Поэтому в математике так важна визуальная интуиция. Доказательства из таких пособий, как и «Евклид Начала: первые 6 книг» и «Доказательства без слов: учебник по визуальному мышлению» даются пониманию при взгляде на их страницы. Я рекомендую эти книги к прочтению каждому, кто интересуется доказательствами других математических проблем.

К примеру, мы помним из школьного курса, что площадь круга вычисляется по формуле ? x r?, но можем ли мы доказать, что эта формула справедлива для каждой возможной окружности?
Величайший из математиков Евклид нашёл доказательства этой формулы настолько простое, что теперь студенты изучают начала интегрального исчисления по нему. Евклид рассуждал так: круг можно поделить на четыре, шесть, шестнадцать, или бесконечно много равных частей, а потом расставить их так, чтобы получился прямоугольник.
Первое что нам нужно сделать — начертить окружность. Затем, мы разделим круг на 8 равных частей и расставим их в похожую на прямоугольник форму. Мы почти получили прямоугольник.

Повторим процесс, на этот раз с 32 равными частями. Если расставить их таким же образом как в предыдущем примере, то мы получим что-то ещё более похожее на прямоугольник.
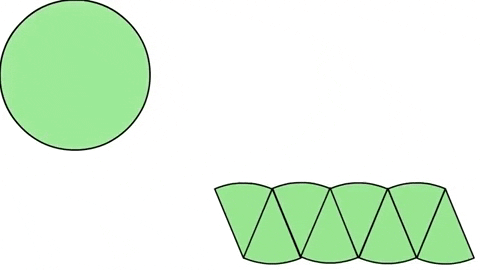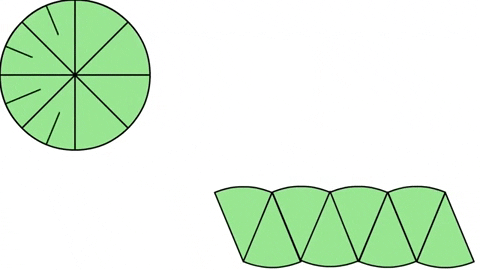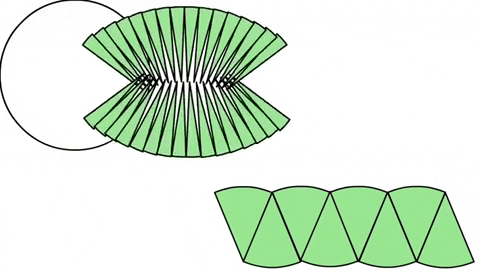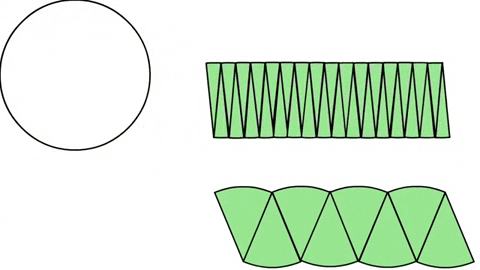
Это значит, что если разделить круг на ещё больше равных частей — происходит удивительное, форма начинает приближаться к идеальному прямоугольнику.

Насколько много должно быть частей чтобы получить идеальный прямоугольник? Для этого его части должны быть бесконечно малыми — такими, что невозможно различить толщину, и стороны становятся почти вертикальными.
Мы знаем, что площадь прямоугольника это его ширина x высота. Высота прямоугольника будет равна радиусу окружности. Чтобы найти ширину, нужно знать длину окружности. Если сравнить ширину прямоугольника и окружность, видно, что ширина это половина от длины окружности. Для длины окружности равной 2?r следует, что ширина должна быть ?r.
Выражение ширина x высота означает тоже самое что ? x r x r. Иными словами — квадрат радиуса, умноженный на ?, то есть ?r?. Это и есть искомый прямоугольник, площадь которого равна площади круга.

Таким образом, ?r? может использоваться для вычисления площади любой из существующих окружностей.


EzikBro
Неудачное название статьи.
Квадратура круга — задача о построении квадрата с площадью равной площади заданного круга. Невозможность такого построения была доказана Линдеманом в конце 19 века, как пишет Википедия. В «Началах» Евклида эта задача не рассматривалась.
askhat Автор
Под «квадратурой» подразумевается площадь, однако «площадь» не такое занимательное слово как «квадратура». Впрочем, если сообщество будет настаивать, заголовок можно изменить.
knotri
упрощать сложно, усложнять легко.
Зачем вы пытаетесь делать что-то "занимательным" (что бы это не значило), а не простым/понятным? Особенно для плохо русско говорящей аудитории с других стран (как например я из Украины)
askhat Автор
Just for fun
BInc
И не просто построения, а с помощью линейки и циркуля, что накладывает дополнительное ограничение, дифференцирование с их помощью не сделаешь.
askhat Автор
Будучи почти историком по образованию, дополню: одно из любимых развлечений древних греков, строить фигуры на песке с помощью веревки и стило, в наше время известно как планиметрия.