В настоящее время Python занимает доминирующую позицию для машинного обучения. Однако, если вы являетесь JS-разработчиком и заинтересованы окунуться в этот мир, то не обязательно включать в свой арсенал новый язык программирования, в связи с появлением TensorFlow.js.
Одним из главных вопросов встает вопрос производительности.
В связи с тем, что машинное обучение — это, по сути, выполнение различного рода математических операций с матрично-подобными данными (тензорами), то библиотека для такого рода вычислений в браузере использует WebGL. Это значительно увеличивает производительность, если бы те же операции осуществлялись на чистом JS. Естественно, библиотека имеет fallback на тот случай, если WebGL по каким-то причинам не поддерживается в браузере (на момент написания статьи caniuse показывает, что поддержка WebGL есть у 97.94% пользователей).
Для повышения производительности на Node.js используется native-binding с TensorFlow. Тут в качестве акселераторов могут служить CPU, GPU и TPU (Tensor Processing Unit)
Необходимо найти уравнение аппроксимирующей линейной функции по заданному набору экспериментальных точек. Иными словами, нам надо найти такую линейную кривую, которая лежала бы наиболее близко к экспериментальным точкам.

Ядром любого машинного обучения будет являться модель, в нашем случае это уравнение линейной функции:
Исходя из условия, мы также имеем набор экспериментальных точек:
Предположим, что на -ом шаге обучения были вычислены следующие коэффициенты линейного уравнения . Сейчас нам необходимо математически выразить на сколько точны подобранные коэффициенты. Для этого нам необходимо посчитать ошибку (loss), которую можно определить, например, по среднеквадратичному отклонению. Tensorflow.js предлагает набор наиболее часто используемых loss функций: tf.metrics.meanAbsoluteError, tf.metrics.meanSquaredError и др.
Цель аппроксимации — минимизация функции ошибки . Воспользуемся для этого методом градиентного спуска. Необходимо:
Например, вычисление значения loss-функции (среднеквадратичное отклонение) выглядело бы так:
Однако, количество входных данных может быть велико. Во время обучения модели нам надо на каждой итерации считать не только значение loss-функции, но и производить более серьезные операции — вычисление градиента. Поэтому, есть смысл использовать tensorflow, который оптимизирует вычисления за счет использования WebGL. Более того, код становится значительно выразительнее, сравните:
Хорошая новость в том, что нам не придется заниматься написанием оптимизаторов для заданной функции ошибки (loss), мы не будем разрабатывать численные методы вычисления частных производных, за нас уже реализовали алгоритм обратного распространения ошибки (backpropogation). Нам лишь потребуется выполнить следующие шаги:
Абсолютно каждый сталкивался с тензорами в математике — это скаляр, вектор, 2D — матрица, 3D — матрица. Тензор — это обобщенное понятие всего перечисленного. Это контейнер данных, который содержит однородные по типу данные (tensorflow поддерживает int32, float32, bool, complex64, string) и имеет определенную форму (количество осей (ранк) и количество элементов в каждой из осей). Ниже мы рассмотрим тензоры вплоть до 3D-матриц, но так как это обобщение, количество осей у тензора может быть столько сколько угодно: 5D, 6D,...ND.
TensorFlow имеет следующий АПИ для создания тензора:
где shape — форма тензора и задается массивом, в котором количество элементов — это количество осей, а каждое значение массива определяет количество элементов вдоль каждой из осей. Например, для задания матрицы размером 4x2 (4 строки, 2 колонки), форма примет вид [4, 2].
Изначально обговорим, что мы будем делать код расширяемым. Линейную аппроксимацию сможем переделать в аппроксимацию экспериментальных точек по функции любого вида. Иерархия классов будет выглядеть следующей:

Начнем реализовывать методы абстрактного класса, за исключением абстрактных методов, которые будут определены в дочерних классах, а тут оставим лишь заглушки с ошибками, если по какой-то причине метод не будет определен в дочернем классе.
Итак, в конструкторе модели мы определили width и height — это реальная ширина и высота плоскости, на котором мы будем расставлять экспериментальные точки. Это необходимо для нормализации входные данные. Т.е. если у нас , то после нормализации мы будем иметь:
optimizerFunction — сделаем задание оптимизатора гибким, для того чтобы была возможность попробовать другие имеющиеся в библиотеке оптимизаторы, по умолчанию мы задали метод Стохастического градиентного спуска tf.train.sgd. Порекомендовал бы также поиграться с другими доступными оптимизаторами, которые во время обучения могут подстраивать learningRate и процесс обучения значительно улучшается, например, попробуйте следующие оптимизаторы: tf.train.momentum, tf.train.adam.
Для того чтобы процесс обучения не был бесконечен мы определили два параметра maxEpochPerTrainSesion и expectedLoss — таким образом мы прекратим процесс обучения или при достижении максимального числа обучающих итераций, или когда значение функции-ошибки станет ниже ожидаемой ошибки (все учтем в методе train ниже).
В конструкторе мы вызываем метод initModelVariables — но как и договаривались, мы ставим заглушку и определим его в дочернем классе позже.
Сейчас реализуем основной метод модели train:
trainSession — это по сути уникальный идентификатор сессии обучения на тот случай, если внешний АПИ будет вызывать train метод, при том что предыдущая сессия обучения еще не завершилась.
Из кода вы видите, что мы из одномерных массивов создаем tensor1d, при этом данные необходимо предварительно нормализовать, функции для нормализации тут:
В цикле для каждого шага обучения мы вызываем оптимизатор модели, которому необходимо передать loss функцию. Как и договаривались, loss-функция у нас будет задана среднеквадратичным отклонением. Тогда пользуясь АПИ tensorflow.js имеем:
Процесс обучения продолжается пока
Также обратите внимание как вызвана loss-функция. Для получения predictedValue — мы вызываем функцию f — которая по сути и будет задавать форму, по которой будет производится регрессия, а в абстрактном классе как и договаривались — ставим заглушку:
На каждом шаге обучения в свойстве объекта модели history мы сохраняем динамику изменения ошибки на каждой эпохе обучения.
После процесса обучения модели мы должны иметь метод, который принимал бы входные параметры и выдавал вычисленные выходные параметры используя обученную модель. Для этого в АПИ мы определили predict метод и выглядит он так:
Обратите внимание на arraySync, по аналогии как node.js, если есть arraySync метод, то однозначно есть и асинхронный метод array, который возвращает Promise. Promise тут нужен, потому что как мы говорили ранее, тензоры все мигрируют в WebGL для ускорения вычислений и процесс становится асинхронным, потому что надо время для перемещения данных с WebGL в JS переменную.
Мы закончили с абстрактным классом, полную версию кода вы можете посмотреть тут:
Для линейной регрессии определим новый класс, который будет унаследован от абстрактного класса, где нам надо определить только два метода initModelVariables и f.
Так как мы работаем над линейной аппроксимацией, то мы должны задать две переменные k, b — и они будут тензорами-скалярами. Для оптимизатора мы должны указать, что они являются настраиваемыми (переменными), а в качестве начальных значений присвоим произвольные числа.
Тут следует рассмотреть АПИ для variable:
Следует обратить внимание на второй аргумент trainable — булевая переменная и по умолчанию она true. Она используется оптимизаторами, что говорит им — необходимо ли при минимизации loss-функции конфигурировать данную переменную. Это может быть полезным, когда мы строим новую модель на базе предварительно обученной модели, загруженной с Keras Python, и мы уверены, что переобучать некоторые слои в этой модели нет необходимости.
Далее нам необходимо определить уравнение аппроксимирующей функции использующей tensorflow API, взгляните на код и вы интуитивно поймете как использовать его:
Например, таким образом вы можете задать квадратичную аппроксимацию:
Здесь вы можете ознакомится с моделями для линейной и квадратичной регрессий:
Ниже приведен код, написанный на React, который использует написанную модель линейной регрессии и создает UX для пользователя:
Результат:
Я бы настоятельно порекомендовал выполнить следующие задания:
Преимущества использования TensorFlow.js в браузере
- интерактивность — браузер имеет много инструментов для визуализации происходящих процессов (графики, анимация и др.);
- сенсоры — браузер имеет прямой доступ к сенсорам устройства (камера, GPS, акселерометр и др.);
- защищенность данных пользователя — нет необходимости отправлять обрабатываемые данные на сервер;
- совместимость с моделями, созданными на Python.
Производительность
Одним из главных вопросов встает вопрос производительности.
В связи с тем, что машинное обучение — это, по сути, выполнение различного рода математических операций с матрично-подобными данными (тензорами), то библиотека для такого рода вычислений в браузере использует WebGL. Это значительно увеличивает производительность, если бы те же операции осуществлялись на чистом JS. Естественно, библиотека имеет fallback на тот случай, если WebGL по каким-то причинам не поддерживается в браузере (на момент написания статьи caniuse показывает, что поддержка WebGL есть у 97.94% пользователей).
Для повышения производительности на Node.js используется native-binding с TensorFlow. Тут в качестве акселераторов могут служить CPU, GPU и TPU (Tensor Processing Unit)
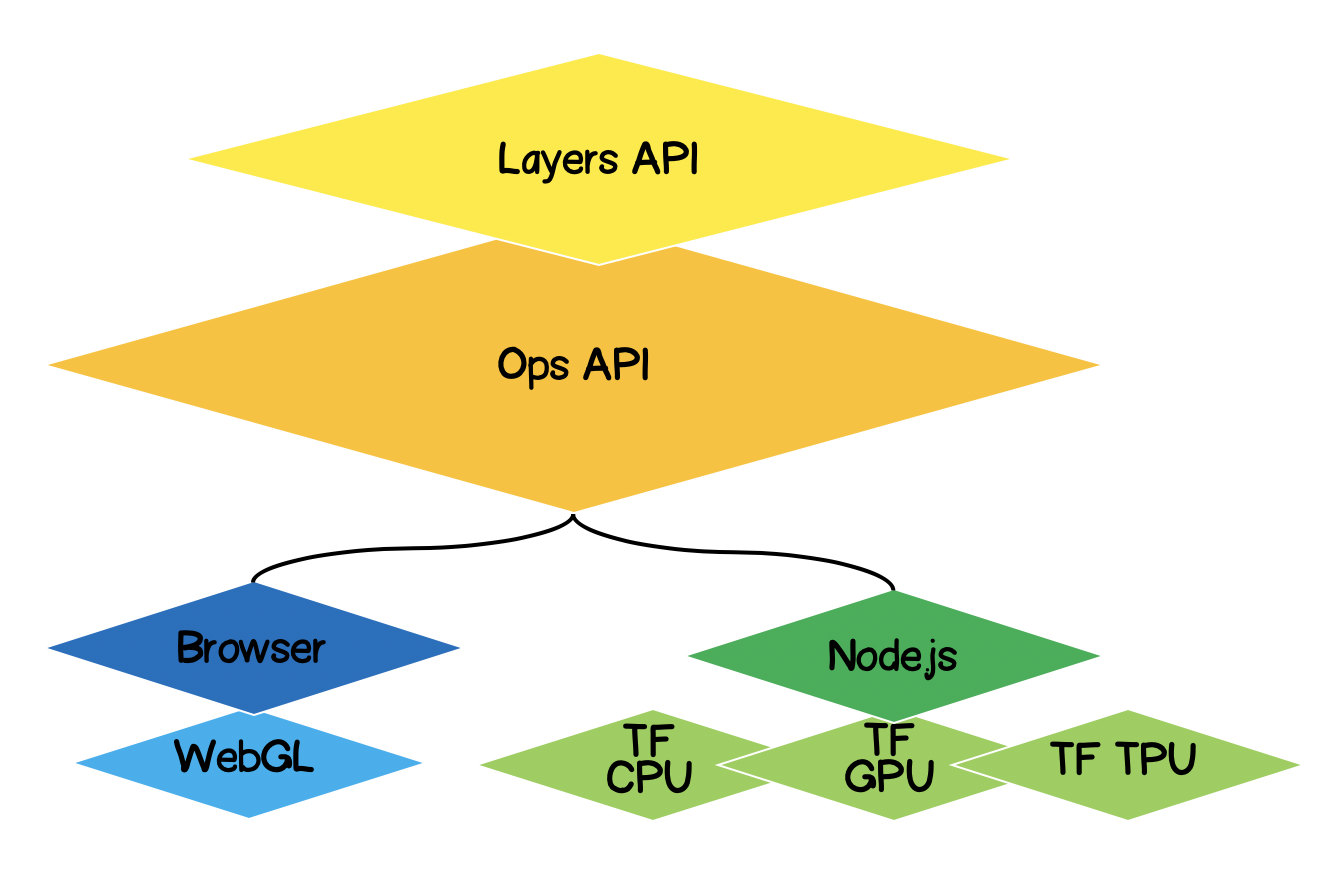
Архитектура TensorFlow.js
- Lowest Layer — этот слой ответственен за параллелизацию вычислений при совершении математических операций над тензорами.
- The Ops API — предоставляет АПИ для осуществления математических операций над тензорами.
- Layers API — позволяет создавать сложные модели нейронных сетей с использованием разных видов слоев (dense, convolutional). Этот слой похож на API Keras на Python и имеет возможность загружать предварительно обученные сети на базе Keras Python.

Постановка задачи
Необходимо найти уравнение аппроксимирующей линейной функции по заданному набору экспериментальных точек. Иными словами, нам надо найти такую линейную кривую, которая лежала бы наиболее близко к экспериментальным точкам.

Формализация решения
Ядром любого машинного обучения будет являться модель, в нашем случае это уравнение линейной функции:
Исходя из условия, мы также имеем набор экспериментальных точек:
Предположим, что на -ом шаге обучения были вычислены следующие коэффициенты линейного уравнения . Сейчас нам необходимо математически выразить на сколько точны подобранные коэффициенты. Для этого нам необходимо посчитать ошибку (loss), которую можно определить, например, по среднеквадратичному отклонению. Tensorflow.js предлагает набор наиболее часто используемых loss функций: tf.metrics.meanAbsoluteError, tf.metrics.meanSquaredError и др.
Цель аппроксимации — минимизация функции ошибки . Воспользуемся для этого методом градиентного спуска. Необходимо:
- — найти вектор-градиент, вычисляя частные производные по коэффициентам ;
- — откорректировать коэффициенты уравнения в направлении обратном направлению вектора-градиента. Таким образом, мы будет минимизировать функцию ошибки:
где — шаг обучения (learning rate) и является одним из настраиваемых параметров модели. Для градиентного спуска он не изменяется на протяжении всего процесса обучения. Маленькое значение learning rate может приводить к долгой сходимости процесса обучения модели и возможному попаданию в локальный минимум (рисунок 2), а сильно большое — может приводить к бесконечному увеличению значения ошибки на каждом шагу обучения, рисунок 1.
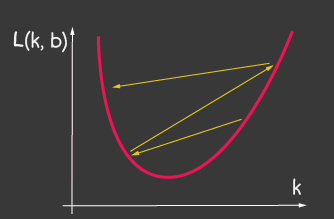 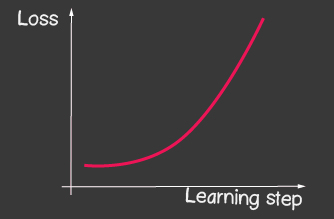 |
  |
|---|---|
| Рисунок 1: Большое значение обучающего шага (learning-rate) | Рисунок 2: Маленькое значение обучающего шага (learning-rate) |
Как это реализовать без Tensorflow.js
Например, вычисление значения loss-функции (среднеквадратичное отклонение) выглядело бы так:
function loss(ysPredicted, ysReal) {
const squaredSum = ysPredicted.reduce(
(sum, yPredicted, i) => sum + (yPredicted - ysReal[i]) ** 2,
0);
return squaredSum / ysPredicted.length;
}
Однако, количество входных данных может быть велико. Во время обучения модели нам надо на каждой итерации считать не только значение loss-функции, но и производить более серьезные операции — вычисление градиента. Поэтому, есть смысл использовать tensorflow, который оптимизирует вычисления за счет использования WebGL. Более того, код становится значительно выразительнее, сравните:
function loss(ysPredicted, ysReal) => {
const ysPredictedTensor = tf.tensor(ysPredicted);
const ysRealTensor = tf.tensor(ysReal);
const loss = ysPredictedTensor.sub(ysRealTensor).square().mean();
return loss.dataSync()[0];
};
Решение с помощью TensorFlow.js
Хорошая новость в том, что нам не придется заниматься написанием оптимизаторов для заданной функции ошибки (loss), мы не будем разрабатывать численные методы вычисления частных производных, за нас уже реализовали алгоритм обратного распространения ошибки (backpropogation). Нам лишь потребуется выполнить следующие шаги:
- задать модель (линейную функцию, в нашем случае);
- описать функцию ошибки (в нашем случае, это среднеквадратичное отклонение)
- выбрать один из реализованных оптимизаторов (есть возможность расширить библиотеку собственной реализацией)
Что такое тензор
Абсолютно каждый сталкивался с тензорами в математике — это скаляр, вектор, 2D — матрица, 3D — матрица. Тензор — это обобщенное понятие всего перечисленного. Это контейнер данных, который содержит однородные по типу данные (tensorflow поддерживает int32, float32, bool, complex64, string) и имеет определенную форму (количество осей (ранк) и количество элементов в каждой из осей). Ниже мы рассмотрим тензоры вплоть до 3D-матриц, но так как это обобщение, количество осей у тензора может быть столько сколько угодно: 5D, 6D,...ND.
TensorFlow имеет следующий АПИ для создания тензора:
tf.tensor (values, shape?, dtype?)где shape — форма тензора и задается массивом, в котором количество элементов — это количество осей, а каждое значение массива определяет количество элементов вдоль каждой из осей. Например, для задания матрицы размером 4x2 (4 строки, 2 колонки), форма примет вид [4, 2].
| Визуализация | Описание |
|---|---|
 |
Скаляр Ранк: 0 Форма: [] JS структура: TensorFlow API: |
 |
Вектор Ранк: 1 Форма: [4] JS структура: TensorFlow API: |
 |
Матрица Ранк: 2 Форма: [4,2] JS структура: TensorFlow API: |
 |
Матрица Ранк: 3 Форма:[4,2,3] JS структура: TensorFlow API: |
Линейная аппроксимация с помощью TensorFlow.js
Изначально обговорим, что мы будем делать код расширяемым. Линейную аппроксимацию сможем переделать в аппроксимацию экспериментальных точек по функции любого вида. Иерархия классов будет выглядеть следующей:

Начнем реализовывать методы абстрактного класса, за исключением абстрактных методов, которые будут определены в дочерних классах, а тут оставим лишь заглушки с ошибками, если по какой-то причине метод не будет определен в дочернем классе.
import * as tf from '@tensorflow/tfjs';
export default class AbstractRegressionModel {
constructor(
width,
height,
optimizerFunction = tf.train.sgd,
maxEpochPerTrainSession = 100,
learningRate = 0.1,
expectedLoss = 0.001
) {
this.width = width;
this.height = height;
this.optimizerFunction = optimizerFunction;
this.expectedLoss = expectedLoss;
this.learningRate = learningRate;
this.maxEpochPerTrainSession = maxEpochPerTrainSession;
this.initModelVariables();
this.trainSession = 0;
this.epochNumber = 0;
this.history = [];
}
}Итак, в конструкторе модели мы определили width и height — это реальная ширина и высота плоскости, на котором мы будем расставлять экспериментальные точки. Это необходимо для нормализации входные данные. Т.е. если у нас , то после нормализации мы будем иметь:
optimizerFunction — сделаем задание оптимизатора гибким, для того чтобы была возможность попробовать другие имеющиеся в библиотеке оптимизаторы, по умолчанию мы задали метод Стохастического градиентного спуска tf.train.sgd. Порекомендовал бы также поиграться с другими доступными оптимизаторами, которые во время обучения могут подстраивать learningRate и процесс обучения значительно улучшается, например, попробуйте следующие оптимизаторы: tf.train.momentum, tf.train.adam.
Для того чтобы процесс обучения не был бесконечен мы определили два параметра maxEpochPerTrainSesion и expectedLoss — таким образом мы прекратим процесс обучения или при достижении максимального числа обучающих итераций, или когда значение функции-ошибки станет ниже ожидаемой ошибки (все учтем в методе train ниже).
В конструкторе мы вызываем метод initModelVariables — но как и договаривались, мы ставим заглушку и определим его в дочернем классе позже.
initModelVariables() {
throw Error('Model variables should be defined')
}
Сейчас реализуем основной метод модели train:
/**
* Train model until explicitly stop process via invocation of stop method
* or loss achieve necessary accuracy, or train achieve max epoch value
*
* @param x - array of x coordinates
* @param y - array of y coordinates
* @param callback - optional, invoked after each training step
*/
async train(x, y, callback) {
const currentTrainSession = ++this.trainSession;
this.lossVal = Number.POSITIVE_INFINITY;
this.epochNumber = 0;
this.history = [];
// convert array into tensors
const input = tf.tensor1d(this.xNormalization(x));
const output = tf.tensor1d(this.yNormalization(y));
while (
currentTrainSession === this.trainSession
&& this.lossVal > this.expectedLoss
&& this.epochNumber <= this.maxEpochPerTrainSession
) {
const optimizer = this.optimizerFunction(this.learningRate);
optimizer.minimize(() => this.loss(this.f(input), output));
this.history = [...this.history, {
epoch: this.epochNumber,
loss: this.lossVal
}];
callback && callback();
this.epochNumber++;
await tf.nextFrame();
}
}
trainSession — это по сути уникальный идентификатор сессии обучения на тот случай, если внешний АПИ будет вызывать train метод, при том что предыдущая сессия обучения еще не завершилась.
Из кода вы видите, что мы из одномерных массивов создаем tensor1d, при этом данные необходимо предварительно нормализовать, функции для нормализации тут:
xNormalization = xs => xs.map(x => x / this.width);
yNormalization = ys => ys.map(y => y / this.height);
yDenormalization = ys => ys.map(y => y * this.height);
В цикле для каждого шага обучения мы вызываем оптимизатор модели, которому необходимо передать loss функцию. Как и договаривались, loss-функция у нас будет задана среднеквадратичным отклонением. Тогда пользуясь АПИ tensorflow.js имеем:
/**
* Calculate loss function as mean-square deviation
*
* @param predictedValue - tensor1d - predicted values of calculated model
* @param realValue - tensor1d - real value of experimental points
*/
loss = (predictedValue, realValue) => {
// L = sum ((x_pred_i - x_real_i)^2) / N
const loss = predictedValue.sub(realValue).square().mean();
this.lossVal = loss.dataSync()[0];
return loss;
};
Процесс обучения продолжается пока
- не будет достигнут лимит по количеству итераций
- не будет достигнута желаемая точность ошибки
- не начат новый обучающий процесс
Также обратите внимание как вызвана loss-функция. Для получения predictedValue — мы вызываем функцию f — которая по сути и будет задавать форму, по которой будет производится регрессия, а в абстрактном классе как и договаривались — ставим заглушку:
f(x) {
throw Error('Model should be defined')
}
На каждом шаге обучения в свойстве объекта модели history мы сохраняем динамику изменения ошибки на каждой эпохе обучения.
После процесса обучения модели мы должны иметь метод, который принимал бы входные параметры и выдавал вычисленные выходные параметры используя обученную модель. Для этого в АПИ мы определили predict метод и выглядит он так:
/**
* Predict value basing on trained model
* @param x - array of x coordinates
* @return Array({x: integer, y: integer}) - predicted values associated with input
*
* */
predict(x) {
const input = tf.tensor1d(this.xNormalization(x));
const output = this.yDenormalization(this.f(input).arraySync());
return output.map((y, i) => ({ x: x[i], y }));
}
Обратите внимание на arraySync, по аналогии как node.js, если есть arraySync метод, то однозначно есть и асинхронный метод array, который возвращает Promise. Promise тут нужен, потому что как мы говорили ранее, тензоры все мигрируют в WebGL для ускорения вычислений и процесс становится асинхронным, потому что надо время для перемещения данных с WebGL в JS переменную.
Мы закончили с абстрактным классом, полную версию кода вы можете посмотреть тут:
AbstractRegressionModel.js
import * as tf from '@tensorflow/tfjs';
export default class AbstractRegressionModel {
constructor(
width,
height,
optimizerFunction = tf.train.sgd,
maxEpochPerTrainSession = 100,
learningRate = 0.1,
expectedLoss = 0.001
) {
this.width = width;
this.height = height;
this.optimizerFunction = optimizerFunction;
this.expectedLoss = expectedLoss;
this.learningRate = learningRate;
this.maxEpochPerTrainSession = maxEpochPerTrainSession;
this.initModelVariables();
this.trainSession = 0;
this.epochNumber = 0;
this.history = [];
}
initModelVariables() {
throw Error('Model variables should be defined')
}
f() {
throw Error('Model should be defined')
}
xNormalization = xs => xs.map(x => x / this.width);
yNormalization = ys => ys.map(y => y / this.height);
yDenormalization = ys => ys.map(y => y * this.height);
/**
* Calculate loss function as mean-squared deviation
*
* @param predictedValue - tensor1d - predicted values of calculated model
* @param realValue - tensor1d - real value of experimental points
*/
loss = (predictedValue, realValue) => {
const loss = predictedValue.sub(realValue).square().mean();
this.lossVal = loss.dataSync()[0];
return loss;
};
/**
* Train model until explicitly stop process via invocation of stop method
* or loss achieve necessary accuracy, or train achieve max epoch value
*
* @param x - array of x coordinates
* @param y - array of y coordinates
* @param callback - optional, invoked after each training step
*/
async train(x, y, callback) {
const currentTrainSession = ++this.trainSession;
this.lossVal = Number.POSITIVE_INFINITY;
this.epochNumber = 0;
this.history = [];
// convert data into tensors
const input = tf.tensor1d(this.xNormalization(x));
const output = tf.tensor1d(this.yNormalization(y));
while (
currentTrainSession === this.trainSession
&& this.lossVal > this.expectedLoss
&& this.epochNumber <= this.maxEpochPerTrainSession
) {
const optimizer = this.optimizerFunction(this.learningRate);
optimizer.minimize(() => this.loss(this.f(input), output));
this.history = [...this.history, {
epoch: this.epochNumber,
loss: this.lossVal
}];
callback && callback();
this.epochNumber++;
await tf.nextFrame();
}
}
stop() {
this.trainSession++;
}
/**
* Predict value basing on trained model
* @param x - array of x coordinates
* @return Array({x: integer, y: integer}) - predicted values associated with input
*
* */
predict(x) {
const input = tf.tensor1d(this.xNormalization(x));
const output = this.yDenormalization(this.f(input).arraySync());
return output.map((y, i) => ({ x: x[i], y }));
}
}
Для линейной регрессии определим новый класс, который будет унаследован от абстрактного класса, где нам надо определить только два метода initModelVariables и f.
Так как мы работаем над линейной аппроксимацией, то мы должны задать две переменные k, b — и они будут тензорами-скалярами. Для оптимизатора мы должны указать, что они являются настраиваемыми (переменными), а в качестве начальных значений присвоим произвольные числа.
initModelVariables() {
this.k = tf.scalar(Math.random()).variable();
this.b = tf.scalar(Math.random()).variable();
}Тут следует рассмотреть АПИ для variable:
tf.variable (initialValue, trainable?, name?, dtype?)Следует обратить внимание на второй аргумент trainable — булевая переменная и по умолчанию она true. Она используется оптимизаторами, что говорит им — необходимо ли при минимизации loss-функции конфигурировать данную переменную. Это может быть полезным, когда мы строим новую модель на базе предварительно обученной модели, загруженной с Keras Python, и мы уверены, что переобучать некоторые слои в этой модели нет необходимости.
Далее нам необходимо определить уравнение аппроксимирующей функции использующей tensorflow API, взгляните на код и вы интуитивно поймете как использовать его:
f(x) {
// y = kx + b
return x.mul(this.k).add(this.b);
}Например, таким образом вы можете задать квадратичную аппроксимацию:
initModelVariables() {
this.a = tf.scalar(Math.random()).variable();
this.b = tf.scalar(Math.random()).variable();
this.c = tf.scalar(Math.random()).variable();
}
f(x) {
// y = ax^2 + bx + c
return this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}Здесь вы можете ознакомится с моделями для линейной и квадратичной регрессий:
LinearRegressionModel.js
import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";
export default class LinearRegressionModel extends AbstractRegressionModel {
initModelVariables() {
this.k = tf.scalar(Math.random()).variable();
this.b = tf.scalar(Math.random()).variable();
}
f = x => x.mul(this.k).add(this.b);
}
QuadraticRegressionModel.js
import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";
export default class QuadraticRegressionModel extends AbstractRegressionModel {
initModelVariables() {
this.a = tf.scalar(Math.random()).variable();
this.b = tf.scalar(Math.random()).variable();
this.c = tf.scalar(Math.random()).variable();
}
f = x => this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}
Ниже приведен код, написанный на React, который использует написанную модель линейной регрессии и создает UX для пользователя:
Regression.js
import React, { useState, useEffect } from 'react';
import Canvas from './components/Canvas';
import LossPlot from './components/LossPlot_v3';
import LinearRegressionModel from './model/LinearRegressionModel';
import './RegressionModel.scss';
const WIDTH = 400;
const HEIGHT = 400;
const LINE_POINT_STEP = 5;
const predictedInput = Array.from({ length: WIDTH / LINE_POINT_STEP + 1 })
.map((v, i) => i * LINE_POINT_STEP);
const model = new LinearRegressionModel(WIDTH, HEIGHT);
export default () => {
const [points, changePoints] = useState([]);
const [curvePoints, changeCurvePoints] = useState([]);
const [lossHistory, changeLossHistory] = useState([]);
useEffect(() => {
if (points.length > 0) {
const input = points.map(({ x }) => x);
const output = points.map(({ y }) => y);
model.train(input, output, () => {
changeCurvePoints(() => model.predict(predictedInput));
changeLossHistory(() => model.history);
});
}
}, [points]);
return (
<div className="regression-low-level">
<div className="regression-low-level__top">
<div className="regression-low-level__workarea">
<div className="regression-low-level__canvas">
<Canvas
width={WIDTH}
height={HEIGHT}
points={points}
curvePoints={curvePoints}
changePoints={changePoints}
/>
</div>
<div className="regression-low-level__toolbar">
<button
className="btn btn-red"
onClick={() => model.stop()}>Stop
</button>
<button
className="btn btn-yellow"
onClick={() => {
model.stop();
changePoints(() => []);
changeCurvePoints(() => []);
}}>Clear
</button>
</div>
</div>
<div className="regression-low-level__loss">
<LossPlot
loss={lossHistory}/>
</div>
</div>
</div>
)
}Результат:
Я бы настоятельно порекомендовал выполнить следующие задания:
- реализовать аппроксимацию функции по логарифмической функции
- для tf.train.sgd оптимизатора попробуйте поиграться с learningRate и понаблюдать как изменяется процесс обучения. Попробуйте задать очень большое значение learningRate, чтобы получить картину, приведенной на рисунке 2
- задайте оптимизатор tf.train.adam. Улучшился ли обучающий процесс. Зависит ли обучающий процесс от изменении learningRate значения в конструкторе модели.

