Статья является продолжением цикла статей, посвященных машинному обучению с использованием библиотеки TensorFlow.JS, в предыдущей статье приведены общая теоретическая часть обучения простейшей нейронной сети, состоящей из одного нейрона:
Машинное обучение. Нейронные сети (часть 1): Процесс обучения персептрона
В данной же статье мы с помощью нейронной сети смоделируем выполнение логических операций OR; XOR, которые являются своеобразным «Hello World» приложением для нейронных сетей.
В статье будет последовательно описан процесс такого моделирования с использованием TensorFlow.js.
Итак построим нейронную сеть для логической операции ИЛИ. На вход мы будем всегда подавать два сигнала X1 и X2, а на выходе будем получать один выходной сигнал Y. Для обучения нейронный сети нам также потребуется тренировочный набор данных (рисунок 1).

Рисунок 1 – Тренировочный набор данных и модель для моделирования логической операции ИЛИ
Чтобы понять какую структуру нейронной сети задать, давайте представим тренировочный набор данных на координатной плоскости с осями X1 и X2 (рисунок 2, слева).
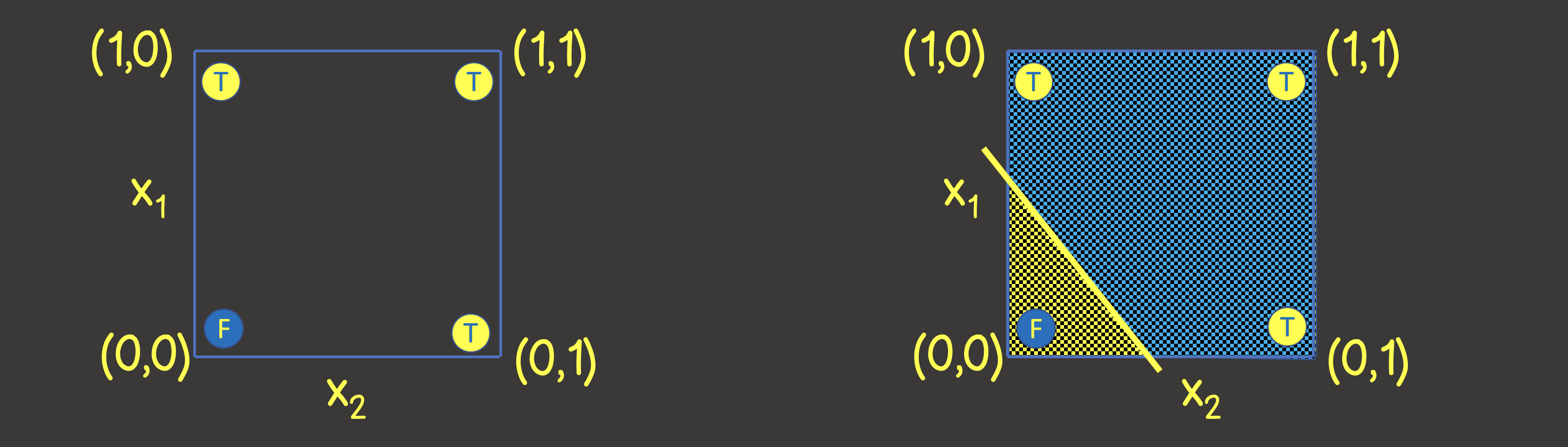
Рисунок 2 – Тренировочный набор на координатной плоскости для логической операции ИЛИ
Обратите внимание, что для решения этой задачи – нам достаточно провести линию, которая разделяла бы плоскость таким образом, чтобы по одну сторону линии были все TRUE значения, а по другую – все FALSE значения (рисунок 2, справа). Мы также знаем, что с этой целью прекрасно может справиться один нейрон в нейронной сети (персептрон), выходное значение которое по входным сигналам вычисляется как:
что является математической записью уравнения прямой.
Ввиду того, что наши значения находятся в промежутке от 0 до 1, то также применим сигмоидную активационную функцию. Таким образом, наша нейронная сеть выглядит так, как на рисунке 3.

Рисунок 3 – Нейронная сеть для обучения логической операции ИЛИ
Итак решим данную задачу с помощью TensorFlow.js.
Для начала нам надо тренировочный набор данных преобразовать в тензоры. Тензор – это контейнер данных, который может иметь осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Для задания тренировочного набора данных первая ось (axis 0) – это всегда ось вдоль которой располагаются все находящиеся в наличии экземпляры выборок данных (рисунок 4).
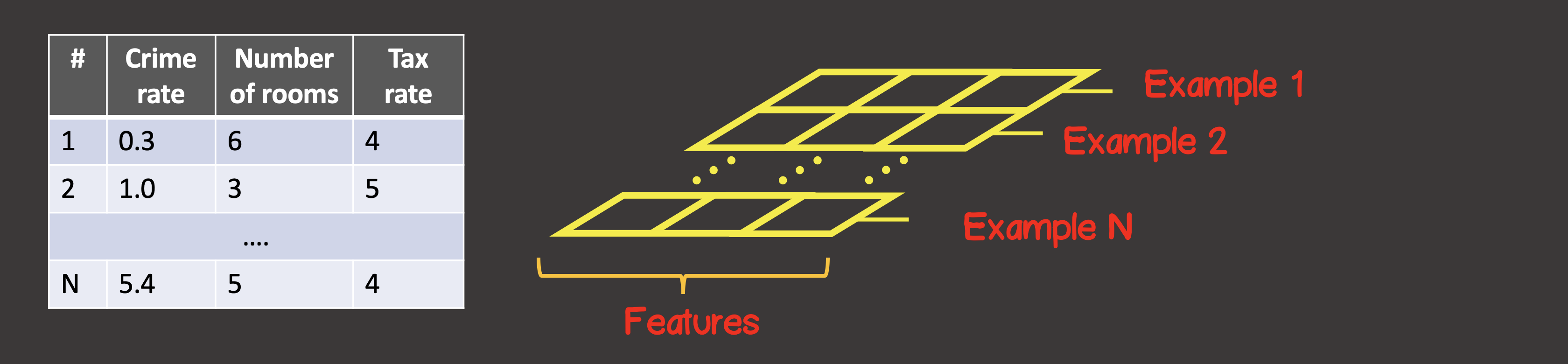
Рисунок 4 – Структура тензора
В нашем конкретном случае мы имеем 4 экземпляра выборок данных (рисунок 1), значит входной тензор вдоль первой оси будет иметь 4 элемента. Каждый элемент тренировочной выборки представляет собой вектор, состоящий из двух элементов X1, X2. Таким образом, входной тензор имеет 2 оси (матрица), вдоль первой оси расположено 4 элемента, вдоль второй оси – 2 элемента.
Аналогично, преобразуем выходные данные в тензор. Как и для входных сигналов, вдоль первой оси — имеем 4 элемента, а в каждом элементе располагается вектор, содержащий одно значение:
Создадим модель, используя TensorFlow API:
Создание модели всегда будет начинаться с вызова tf.sequential(). Основным строительным блоком модели – это слои. Мы можем подключать к модели столько слоев в нейронную сеть, сколько нам надо. Тут мы используем dense слой, что означает что каждый нейрон последующего слоя имеет связь с каждым нейроном предыдущего слоя. Например, если у нас есть два dense слоя, в первом слое нейронов, а во втором – , то общее число соединений между слоями будет .
В нашем случае как видим – нейронная сеть состоит из одного слоя, в котором один нейрон, поэтому units задан единице.
Также для первого слоя нейронной сети мы обязательно должны задать inputShape, так как у нас каждый входной экземпляр представлен вектором из двух значений X1 и X2, поэтому inputShape=[2]. Обратите внимание, что задавать inputShape для промежуточных слоев нет необходимости — TensorFlow может определить эту величину по значению units предыдущего слоя.
Также каждому слою в случае необходимости можно задать активационную функцию, мы определились выше, что это будет сигмоидная функция. Доступные на данных момент активационные функции в TensorFlow можно найти здесь.
Далее нам надо откомпилировать модель (см АПИ здесь), при этом нам надо задать два обязательных параметра – это функция-ошибки и вид оптимизатора, который будет искать ее минимум:
Мы задали в качестве оптимизатора stochastic gradient descent с обучающим шагом 0.1.
Список реализованных оптимизаторов в библиотеке: tf.train.sgd, tf.train.momentum, tf.train.adagrad, tf.train.adadelta, tf.train.adam, tf.train.adamax, tf.train.rmsprop.
В качестве функции ошибки задана функцией среднеквадратичной ошибки:
Модель задана, и следующим шагом является процесс обучения модели, для этого у модели должен быть вызван метод fit:
Мы задали, что процесс обучения должен состоять из 100 обучающих шагов (количество эпох обучений); также на каждой очередной эпохе – входные данные следует перетасовать в произвольном порядке (shuffle=true) – что ускорит процесс сходимости модели, так в нашем тренировочном наборе данных мало экземпляров (4).
После завершения процесса обучения – мы можем использовать predict метод, который по новым входным сигналам, будет вычислять выходное значение.
Метод generateInputs – просто создает набор тестовых данных с количеством элементов 10x10, которые делят координатную плоскость на 100 квадратов:
На следующем рисунке вы увидите частично процесс обучения:

Моделирование логической операции XOR
Тренировочный набор для данной функции приведен на рисунке 6, а также расставим эти точки также как делали для логической операции ИЛИ на координатной плоскости
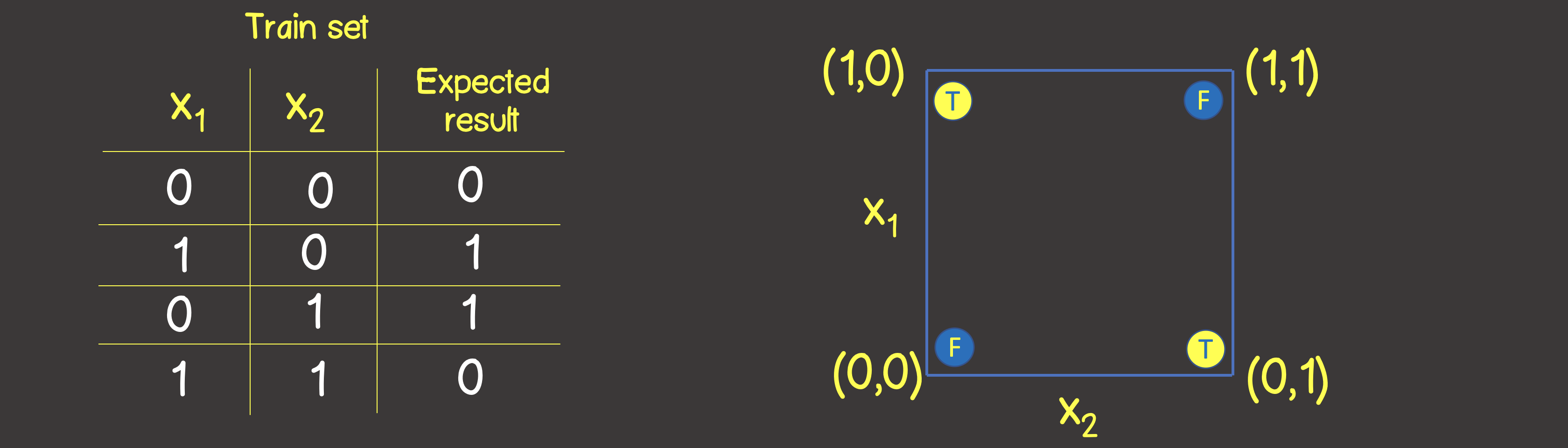
Рисунок 6 — Тренировочный набор данных и модель для моделирования логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
Обратите внимание, что в отличии от логической операции ИЛИ – вы не сможете разделить плоскость одной прямой линией, чтобы по одну сторону находились все TRUE значения, а по другую сторону – все FALSE. Однако, мы это можем сделать с помощью двух кривых (рисунок 7).
Очевидно, что в данном случае одним нейроном в слое не обойтись – нужен как минимум дополнительно еще один слой с двумя нейронами, каждый из которых определил бы одну из двух линий на плоскости.
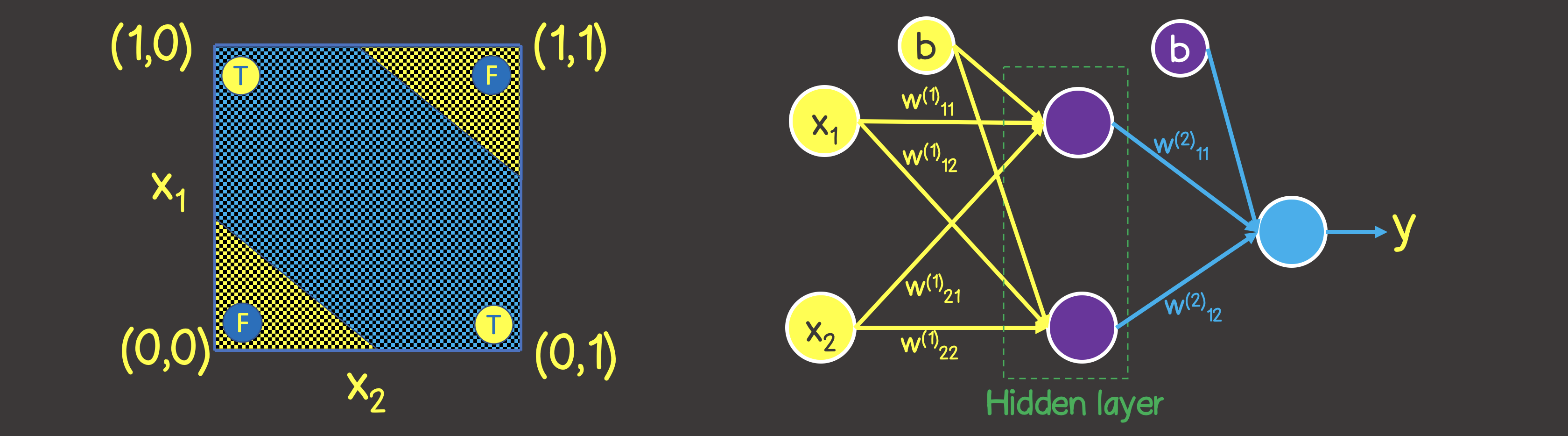
Рисунок 7 – Модель нейронной сети для логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
В прошлом коде нам необходимо сделать изменения в нескольких местах, одни из которых — это непосредственно сам тренировочный набор данных:
Вторым местом — это изменившаяся структура модели, согласно рисунку 7:
Процесс обучения в этом случае выглядит так:

Тема следующей статьи
В следующей статье мы опишем каким образом решать задачи, связанных с классификацией объектов по категориям, базируясь на списке каких-то признаков.
Машинное обучение. Нейронные сети (часть 1): Процесс обучения персептрона
В данной же статье мы с помощью нейронной сети смоделируем выполнение логических операций OR; XOR, которые являются своеобразным «Hello World» приложением для нейронных сетей.
В статье будет последовательно описан процесс такого моделирования с использованием TensorFlow.js.
Итак построим нейронную сеть для логической операции ИЛИ. На вход мы будем всегда подавать два сигнала X1 и X2, а на выходе будем получать один выходной сигнал Y. Для обучения нейронный сети нам также потребуется тренировочный набор данных (рисунок 1).

Рисунок 1 – Тренировочный набор данных и модель для моделирования логической операции ИЛИ
Чтобы понять какую структуру нейронной сети задать, давайте представим тренировочный набор данных на координатной плоскости с осями X1 и X2 (рисунок 2, слева).
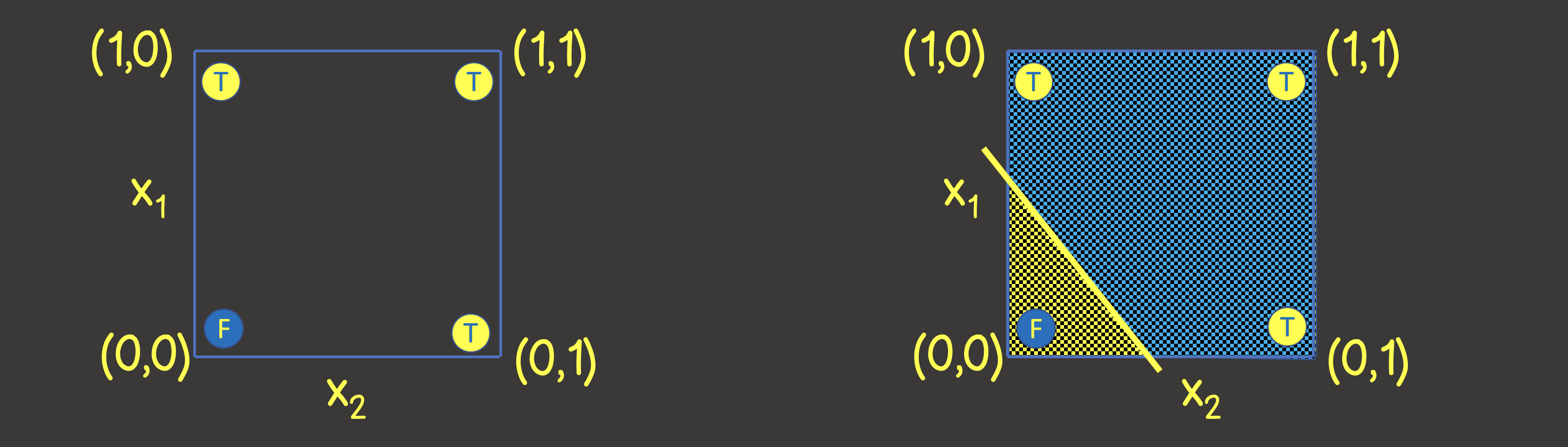
Рисунок 2 – Тренировочный набор на координатной плоскости для логической операции ИЛИ
Обратите внимание, что для решения этой задачи – нам достаточно провести линию, которая разделяла бы плоскость таким образом, чтобы по одну сторону линии были все TRUE значения, а по другую – все FALSE значения (рисунок 2, справа). Мы также знаем, что с этой целью прекрасно может справиться один нейрон в нейронной сети (персептрон), выходное значение которое по входным сигналам вычисляется как:
что является математической записью уравнения прямой.
Ввиду того, что наши значения находятся в промежутке от 0 до 1, то также применим сигмоидную активационную функцию. Таким образом, наша нейронная сеть выглядит так, как на рисунке 3.

Рисунок 3 – Нейронная сеть для обучения логической операции ИЛИ
Итак решим данную задачу с помощью TensorFlow.js.
Для начала нам надо тренировочный набор данных преобразовать в тензоры. Тензор – это контейнер данных, который может иметь осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Для задания тренировочного набора данных первая ось (axis 0) – это всегда ось вдоль которой располагаются все находящиеся в наличии экземпляры выборок данных (рисунок 4).

Рисунок 4 – Структура тензора
В нашем конкретном случае мы имеем 4 экземпляра выборок данных (рисунок 1), значит входной тензор вдоль первой оси будет иметь 4 элемента. Каждый элемент тренировочной выборки представляет собой вектор, состоящий из двух элементов X1, X2. Таким образом, входной тензор имеет 2 оси (матрица), вдоль первой оси расположено 4 элемента, вдоль второй оси – 2 элемента.
const input = [[0, 0], [1, 0], [0, 1], [1, 1]];
const inputTensor = tf.tensor(input, [input.length, 2]);
Аналогично, преобразуем выходные данные в тензор. Как и для входных сигналов, вдоль первой оси — имеем 4 элемента, а в каждом элементе располагается вектор, содержащий одно значение:
const output = [[0], [1], [1], [1]]
const outputTensor = tf.tensor(output, [output.length, 1]);
Создадим модель, используя TensorFlow API:
const model = tf.sequential();
model.add(
tf.layers.dense({ inputShape: [2], units: 1, activation: 'sigmoid' })
);
Создание модели всегда будет начинаться с вызова tf.sequential(). Основным строительным блоком модели – это слои. Мы можем подключать к модели столько слоев в нейронную сеть, сколько нам надо. Тут мы используем dense слой, что означает что каждый нейрон последующего слоя имеет связь с каждым нейроном предыдущего слоя. Например, если у нас есть два dense слоя, в первом слое нейронов, а во втором – , то общее число соединений между слоями будет .
В нашем случае как видим – нейронная сеть состоит из одного слоя, в котором один нейрон, поэтому units задан единице.
Также для первого слоя нейронной сети мы обязательно должны задать inputShape, так как у нас каждый входной экземпляр представлен вектором из двух значений X1 и X2, поэтому inputShape=[2]. Обратите внимание, что задавать inputShape для промежуточных слоев нет необходимости — TensorFlow может определить эту величину по значению units предыдущего слоя.
Также каждому слою в случае необходимости можно задать активационную функцию, мы определились выше, что это будет сигмоидная функция. Доступные на данных момент активационные функции в TensorFlow можно найти здесь.
Далее нам надо откомпилировать модель (см АПИ здесь), при этом нам надо задать два обязательных параметра – это функция-ошибки и вид оптимизатора, который будет искать ее минимум:
model.compile({
optimizer: tf.train.sgd(0.1),
loss: 'meanSquaredError'
});
Мы задали в качестве оптимизатора stochastic gradient descent с обучающим шагом 0.1.
Список реализованных оптимизаторов в библиотеке: tf.train.sgd, tf.train.momentum, tf.train.adagrad, tf.train.adadelta, tf.train.adam, tf.train.adamax, tf.train.rmsprop.
На практике по умолчанию сразу можно выбирать adam оптимизатор, который имеет лучшие показатели сходимости модели, в отличии от sgd – обучающий шаг (learning rate) на каждом этапе обучения задается в зависимости от истории предыдущих шагов и не является постоянным на протяжении всего процесса обучения.
В качестве функции ошибки задана функцией среднеквадратичной ошибки:
Модель задана, и следующим шагом является процесс обучения модели, для этого у модели должен быть вызван метод fit:
async function initModel() {
// skip for brevity
await model.fit(trainingInputTensor, trainingOutputTensor, {
epochs: 1000,
shuffle: true,
callbacks: {
onEpochEnd: async (epoch, { loss }) => {
// any actions on during any epoch of training
await tf.nextFrame();
}
}
})
}
Мы задали, что процесс обучения должен состоять из 100 обучающих шагов (количество эпох обучений); также на каждой очередной эпохе – входные данные следует перетасовать в произвольном порядке (shuffle=true) – что ускорит процесс сходимости модели, так в нашем тренировочном наборе данных мало экземпляров (4).
После завершения процесса обучения – мы можем использовать predict метод, который по новым входным сигналам, будет вычислять выходное значение.
const testInput = generateInputs(10);
const testInputTensor = tf.tensor(testInput, [testInput.length, 2]);
const output = model.predict(testInputTensor).arraySync();
Метод generateInputs – просто создает набор тестовых данных с количеством элементов 10x10, которые делят координатную плоскость на 100 квадратов:
Полный код приведен тут
import React, { useEffect, useState } from 'react';
import LossPlot from './components/LossPlot';
import Canvas from './components/Canvas';
import * as tf from "@tensorflow/tfjs";
let model;
export default () => {
const [data, changeData] = useState([]);
const [lossHistory, changeLossHistory] = useState([]);
useEffect(() => {
async function initModel() {
const input = [[0, 0], [1, 0], [0, 1], [1, 1]];
const inputTensor = tf.tensor(input, [input.length, 2]);
const output = [[0], [1], [1], [1]]
const outputTensor = tf.tensor(output, [output.length, 1]);
const testInput = generateInputs(10);
const testInputTensor = tf.tensor(testInput, [testInput.length, 2]);
model = tf.sequential();
model.add(
tf.layers.dense({ inputShape:[2], units:1, activation: 'sigmoid'})
);
model.compile({
optimizer: tf.train.adam(0.1),
loss: 'meanSquaredError'
});
await model.fit(inputTensor, outputTensor, {
epochs: 100,
shuffle: true,
callbacks: {
onEpochEnd: async (epoch, { loss }) => {
changeLossHistory((prevHistory) => [...prevHistory, {
epoch,
loss
}]);
const output = model.predict(testInputTensor)
.arraySync();
changeData(() => output.map(([out], i) => ({
out,
x1: testInput[i][0],
x2: testInput[i][1]
})));
await tf.nextFrame();
}
}
})
}
initModel();
}, []);
return (
<div>
<Canvas data={data} squareAmount={10}/>
<LossPlot loss={lossHistory}/>
</div>
);
}
function generateInputs(squareAmount) {
const step = 1 / squareAmount;
const input = [];
for (let i = 0; i < 1; i += step) {
for (let j = 0; j < 1; j += step) {
input.push([i, j]);
}
}
return input;
}
На следующем рисунке вы увидите частично процесс обучения:

Реализация в планкере:
Моделирование логической операции XOR
Тренировочный набор для данной функции приведен на рисунке 6, а также расставим эти точки также как делали для логической операции ИЛИ на координатной плоскости

Рисунок 6 — Тренировочный набор данных и модель для моделирования логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
Обратите внимание, что в отличии от логической операции ИЛИ – вы не сможете разделить плоскость одной прямой линией, чтобы по одну сторону находились все TRUE значения, а по другую сторону – все FALSE. Однако, мы это можем сделать с помощью двух кривых (рисунок 7).
Очевидно, что в данном случае одним нейроном в слое не обойтись – нужен как минимум дополнительно еще один слой с двумя нейронами, каждый из которых определил бы одну из двух линий на плоскости.

Рисунок 7 – Модель нейронной сети для логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR)
В прошлом коде нам необходимо сделать изменения в нескольких местах, одни из которых — это непосредственно сам тренировочный набор данных:
const input = [[0, 0], [1, 0], [0, 1], [1, 1]];
const inputTensor = tf.tensor(input, [input.length, 2]);
const output = [[0], [1], [1], [0]]
const outputTensor = tf.tensor(output, [output.length, 1]);
Вторым местом — это изменившаяся структура модели, согласно рисунку 7:
model = tf.sequential();
model.add(
tf.layers.dense({ inputShape: [2], units: 2, activation: 'sigmoid' })
);
model.add(
tf.layers.dense({ units: 1, activation: 'sigmoid' })
);
Процесс обучения в этом случае выглядит так:

Реализация в планкере:
Тема следующей статьи
В следующей статье мы опишем каким образом решать задачи, связанных с классификацией объектов по категориям, базируясь на списке каких-то признаков.

