
Даниэль Лемир – профессор Заочного квебекского университета (TELUQ), придумавший способ очень быстро парсить double – совместно с инженером Джоном Кайзером из Microsoft опубликовали ещё одну свою находку: валидатор UTF-8, обгоняющий библиотеку UTF-8 CPP (2006) в 48..77 раз, ДКА от Бьёрна Хёрманна (2009) – в 20..45 раз, и алгоритм Google Fuchsia (2020) – в 13..35 раз. Новость об этой публикации на хабре уже постили, но без технических подробностей; так что восполняем этот недочёт.
Требования UTF-8
Для начала вспомним, что Unicode допускает code points от U+0000 до U+10FFFF, которые кодируются в UTF-8 последовательностями от 1 до 4 байтов:
| Число байтов в кодировке | Число битов в code point | Минимальное значение | Максимальное значение |
|---|---|---|---|
| 1 | 1..7 | U+0000 = 00000000 | U+007F = 01111111 |
| 2 | 8..11 | U+0080 = 11000010 10000000 | U+07FF = 11011111 10111111 |
| 3 | 12..16 | U+0800 = 11100000 10100000 10000000 | U+FFFF = 11101111 10111111 10111111 |
| 4 | 17..21 | U+010000 = 11110000 10010000 10000000 10000000 | U+10FFFF = 11110100 10001111 10111111 10111111 |
По правилам кодирования, старшие биты первого байта последовательности определяют общее количество байтов в последовательности; нулевой старший бит может быть только у однобайтных (ASCII) символов, единичные два старших бита обозначают многобайтного символа, единичный и нулевой – продолжающий байт> многобайтного символа.
Какого рода ошибки могут быть в строке, закодированной таким образом?
- Незаконченная последовательность: на месте, где ожидался продолжающий байт, встретился ведущий байт или ASCII-символ;
- Неначатая последовательность: на месте, где ожидался ведущий байт или ASCII-символ, встретился продолжающий байт;
- Слишком длинная последовательность: ведущий байт
11111xxxсоответствует пятибайтной или более длинной последовательности, запрещённой в UTF-8; - Выход за границы Unicode: после расшифровки четырёхбайтной последовательности получился code point выше U+10FFFF.
Если в строке нет ни одной из этих четырёх ошибок, то её можно расшифровать в последовательность корректных code points. UTF-8, однако, требует большего – чтобы каждая последовательность корректных code points кодировалась единственным образом. Это добавляет ещё два рода возможных ошибок:
- Неминимальная последовательность: для расшифрованного code point возможна более короткая кодировка;
- Суррогаты: code points в диапазоне от U+D800 до U+DFFF зарезервированы для UTF-16, и последовательность из двух таких суррогатов обозначает code point выше U+FFFF. UTF-8 требует, чтобы такие code points кодировались напрямую, а не как пары суррогатов.
В редко используемой кодировке CESU-8 последнее требование отменено (а в MUTF-8 – ещё и предпоследнее), благодаря чему длина последовательности ограничена тремя байтами, но расшифровка и валидация строк усложняются. Например, смайлик U+1F600 GRINNING FACE представляется в UTF-16 парой суррогатов
0xD83D 0xDE00, и CESU-8/MUTF-8 переводят её в пару трёхбайтных последовательностей 0xED 0xA0 0xBD 0xED 0xB8 0x80; но в UTF-8 этот смайлик кодируется одной четырёхбайтной последовательностью 0xF0 0x9F 0x98 0x80.Для каждого рода ошибки ниже перечислены последовательности битов, которые к ней приводят:
| Незаконченная последовательность | Недостаёт 2-ого байта | 11xxxxxx 0xxxxxxx |
11xxxxxx 11xxxxxx |
||
| Недостаёт 3-его байта | 111xxxxx 10xxxxxx 0xxxxxxx |
|
111xxxxx 10xxxxxx 11xxxxxx |
||
| Недостаёт 4-ого байта | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx |
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx |
||
| Неначатая последовательность | Лишний 2-ой байт | 0xxxxxxx 10xxxxxx |
| Лишний 3-ий байт | 110xxxxx 10xxxxxx 10xxxxxx |
|
| Лишний 4-ый байт | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx |
|
| Лишний 5-ый байт | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx |
|
| Слишком длинная последовательность | 11111xxx |
|
| Выход за границы Unicode | U+110000..U+13FFFF | 11110100 1001xxxx |
11110100 101xxxxx |
||
| ? U+140000 | 11110101 |
|
1111011x |
||
| Неминимальная последовательность | 2-байтная | 1100000x |
| 3-байтная | 11100000 100xxxxx |
|
| 4-байтная | 11110000 1000xxxx |
|
| Суррогаты | 11101101 101xxxxx |
|
Валидация UTF-8
При наивном подходе, использованном в библиотеке UTF-8 CPP серба Неманьи Трифуновича, валидация выполняется каскадом вложенных ветвлений:
const octet_difference_type length = utf8::internal::sequence_length(it);
// Get trail octets and calculate the code point
utf_error err = UTF8_OK;
switch (length) {
case 0:
return INVALID_LEAD;
case 1:
err = utf8::internal::get_sequence_1(it, end, cp);
break;
case 2:
err = utf8::internal::get_sequence_2(it, end, cp);
break;
case 3:
err = utf8::internal::get_sequence_3(it, end, cp);
break;
case 4:
err = utf8::internal::get_sequence_4(it, end, cp);
break;
}
if (err == UTF8_OK) {
// Decoding succeeded. Now, security checks...
if (utf8::internal::is_code_point_valid(cp)) {
if (!utf8::internal::is_overlong_sequence(cp, length)){
// Passed! Return here.
Внутри
sequence_length() и is_overlong_sequence() тоже ветвления в зависимости от длины последовательности. Если во входной строке непредсказуемо чередуются последовательности разной длины, то предсказатель переходов не сможет избежать сброса конвеера по нескольку раз на каждом обрабатываемом символе.Более эффективный подход к валидации UTF-8 заключается в использовании конечного автомата из 9 состояний: (состояние ошибки на диаграмме не показано)
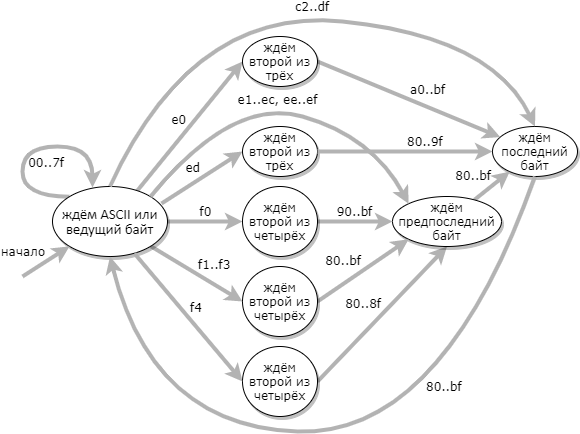
Когда таблица переходов автомата составлена, то код валидатора получается очень простым:
uint32_t type = utf8d[byte];
*codep = (*state != UTF8_ACCEPT) ?
(byte & 0x3fu) | (*codep << 6) :
(0xff >> type) & (byte);
*state = utf8d[256 + *state + type];
Здесь для каждого обрабатываемого символа повторяются одни и те же действия, без условных переходов – поэтому сбросов конвеера не потребуется; с другой стороны, на каждой итерации осуществляется дополнительный доступ к памяти (к таблице переходов
utf8d) впридачу ко чтению входного символа.Лемир и Кайзер взяли за основу своего валидатора этот же ДКА, и достигли ускорения в десятки раз за счёт применения трёх усовершенствований:
- Таблицу переходов удалось ужать с 364 байтов до 48, так что она целиком помещается в трёх векторных регистрах (по 128 бит), и обращения к памяти требуются только для чтения входных символов;
- Блоки по 16 соседних байтов обрабатываются параллельно;
- Если 16-байтный блок целиком состоит из ASCII-символов – то он заведомо корректный, и нет нужды в более тщательной проверке. Этот «срез пути» ускоряет обработку «реалистичных» текстов, содержащих целые предложения латиницей, в два-три раза; но на случайных текстах, где латиница, иероглифы и смайлики равномерно перемешаны, это ускорения не даёт.
В реализации каждого из этих усовершенствований есть неочевидные тонкости, так что их стоит рассмотреть подробно.
Уменьшение таблицы переходов
Первое усовершенствование основывается на том наблюдении, что для обнаружения большинства ошибок (12 недопустимых последовательностей битов из 19 перечисленных в таблице выше) достаточно проверить 12 первых битов последовательности:
| Незаконченная последовательность | Недостаёт 2-ого байта | 11xxxxxx 0xxxxxxx |
0x02 |
11xxxxxx 11xxxxxx |
|||
| Неначатая последовательность | Лишний 2-ой байт | 0xxxxxxx 10xxxxxx |
0x01 |
| Слишком длинная последовательность | 11111xxx 1000xxxx |
0x20 |
|
11111xxx 1001xxxx |
0x40 |
||
11111xxx 101xxxxx |
|||
| Выход за границы Unicode | U+1[1235679ABDEF]xxxx | 111101xx 1001xxxx |
|
111101xx 101xxxxx |
|||
| U+1[48C]xxxx | 11110101 1000xxxx |
0x20 |
|
1111011x 1000xxxx |
|||
| Неминимальная последовательность | 2-байтная | 1100000x |
0x04 |
| 3-байтная | 11100000 100xxxxx |
0x10 |
|
| 4-байтная | 11110000 1000xxxx |
0x20 |
|
| Суррогаты | 11101101 101xxxxx |
0x08 |
|
Каждой из этих возможных ошибок исследователи присвоили один из семи битов, как показано в самом правом столбце. (Присвоенные биты различаются между их опубликованной статьёй и их кодом на GitHub; здесь взяты значения из статьи.) Для того, чтобы обойтись семью битами, два подслучая выхода за границы Unicode пришлось переразбить так, чтобы второй объединялся с 4-байтной неминимальной последовательностью; а случай слишком длинной последовательности разбит на три подслучая и объединён с подслучаями выхода за границы Unicode.
Таким образом с ДКА Хёрманна были произведены следующие изменения:
- Вход поступает не по байту, а по тетраде (полубайту);
- Автомат используется как недетерминированный – обработка каждой тетрады переводит автомат между подмножествами всех возможных состояний;
- Восемь корректных состояний объединены в одно, зато одно ошибочное разделено на семь;
- Три соседние тетрады обрабатываются не последовательно, а независимо друг от друга, и результат получается как пересечение трёх множеств конечных состояний.
Благодаря этим изменениям, для описания всех возможных переходов достаточно трёх таблиц по 16 байт: каждый элемент таблицы используется как битовое поле, перечисляющее все возможные конечные состояния. Три таких элемента объединяются по AND, и если в результате есть ненулевые биты, значит, обнаружена ошибка.
| Тетрада | Значение | Возможные ошибки | Код |
|---|---|---|---|
| Старшая в первом байте | 0–7 | Лишний 2-ой байт | 0x01 |
| 8–11 | (нет) | 0x00 |
|
| 12 | Недостаёт 2-ого байта; 2-байтная неминимальная последовательность | 0x06 |
|
| 13 | Недостаёт 2-ого байта | 0x02 |
|
| 14 | Недостаёт 2-ого байта; 2-байтная неминимальная последовательность; суррогаты | 0x0E |
|
| 15 | Недостаёт 2-ого байта; слишком длинная последовательность; выход за границы Unicode; 4-байтная неминимальная последовательность | 0x62 |
|
| Младшая в первом байте | 0 | Недостаёт 2-ого байта; лишний 2-ой байт; неминимальная последовательность | 0x37 |
| 1 | Недостаёт 2-ого байта; лишний 2-ой байт; 2-байтная неминимальная последовательность | 0x07 |
|
| 2–3 | Недостаёт 2-ого байта; лишний 2-ой байт | 0x03 |
|
| 4 | Недостаёт 2-ого байта; лишний 2-ой байт; выход за границы Unicode | 0x43 |
|
| 5–7 | 0x63 |
||
| 8–10, 12–15 | Недостаёт 2-ого байта; лишний 2-ой байт; слишком длинная последовательность | ||
| 11 | Недостаёт 2-ого байта; лишний 2-ой байт; слишком длинная последовательность; суррогаты | 0x6B |
|
| Старшая во втором байте | 0–7, 12–15 | Недостаёт 2-ого байта; слишком длинная последовательность; 2-байтная неминимальная последовательность | 0x06 |
| 8 | Лишний 2-ой байт; слишком длинная последовательность; выход за границы Unicode; неминимальная последовательность | 0x35 |
|
| 9 | 0x55 |
||
| 10–11 | Лишний 2-ой байт; слишком длинная последовательность; выход за границы Unicode; 2-байтная неминимальная последовательность; суррогаты | 0x4D |
Остались необработанными ещё 7 недопустимых последовательностей битов:
| Незаконченная последовательность | Недостаёт 3-его байта | 111xxxxx 10xxxxxx 0xxxxxxx |
111xxxxx 10xxxxxx 11xxxxxx |
||
| Недостаёт 4-ого байта | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx |
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx |
||
| Неначатая последовательность | Лишний 3-ий байт | 110xxxxx 10xxxxxx 10xxxxxx |
| Лишний 4-ый байт | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx |
|
| Лишний 5-ый байт | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx |
И здесь пригождается старший бит, предусмотрительно оставленный в таблицах переходов неиспользованным: он будет соответствовать последовательности битов
10xxxxxx 10xxxxxx, т.е. двум продолжающим байтам подряд. Теперь проверка трёх тетрад может либо обнаружить ошибку, либо дать результат 0x00 или 0x80. И вот этого результата первой проверки – вместе с первой тетрадой – нам уже достаточно:| Недостаёт 3-его байта | 111xxxxx 10xxxxxx 0xxxxxxx |
|
111xxxxx 10xxxxxx 11xxxxxx |
||
| Недостаёт 4-ого байта | 1111xxxx 10xxxxxx 10xxxxxx 0xxxxxxx |
|
1111xxxx 10xxxxxx 10xxxxxx 11xxxxxx |
||
| Лишний 3-ий байт | 110xxxxx 10xxxxxx 10xxxxxx |
|
| Лишний 4-ый байт | 1110xxxx 10xxxxxx 10xxxxxx 10xxxxxx |
|
| Лишний 5-ый байт | 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx |
|
| Допустимые комбинации | |
|
|
||
Значит, для завершения проверки достаточно убедиться, что каждый результат
0x80 соответствует одной из двух допустимых комбинаций.Векторизация
Как обрабатывать блоки по 16 соседних байтов параллельно? Центральная идея состоит в том, чтобы использовать инструкцию
pshufb как 16 одновременных подстановок в соответствии с 16-байтной таблицей. Для второй проверки нужно найти в блоке все байты вида 111xxxxx и 1111xxxx; поскольку на Intel нет беззнакового векторного сравнения, то оно заменяется вычитанием с насыщением (psubusb).Исходники simdjson тяжеловато читаются из-за того, что весь код разбит на однострочные функции. Псевдокод всего валидатора целиком выглядит примерно так:
prev = vector(0)
while !input_exhausted:
input = vector(...)
prev1 = prev<<120 | input>>8
prev2 = prev<<112 | input>>16
prev3 = prev<<104 | input>>24
# первая проверка
nibble1 = prev1.shr(4).lookup(table1)
nibble2 = prev1.and(15).lookup(table2)
nibble3 = input.shr(4).lookup(table3)
result1 = nibble1 & nibble2 & nibble3
# вторая проверка
test1 = prev2.saturating_sub(0xDF) # 111xxxxx => >0
test2 = prev3.saturating_sub(0xEF) # 1111xxxx => >0
result2 = (test1 | test2).gt(0) & vector(0x80)
# в result1 должны быть 0x80 на тех же местах, как и в result2,
# и нули на всех остальных
if result1 != result2:
return false
prev = input
return true
Если некорректная последовательность находится у правого края самого последнего блока, то она этим кодом не будет обнаружена. Чтобы не заморачиваться, можно дополнить входную строку нулевыми байтами так, чтобы в конце получился один полностью нулевой блок. В simdjson предпочли вместо этого реализовать особую проверку для последних байтов: для корректности строки нужно, чтобы самый последний байт был строго меньше
0xC0, предпоследний – строго меньше 0xE0, и третий с конца – строго меньше 0xF0.Последнее из усовершенствований, придуманных Лемиром и Кайзером – это «срез пути» для ASCII. Определить, что в текущем блоке есть только ASCII-символы, очень просто:
input & vector(0x80) == vector(0). В этом случае достаточно убедиться, что нет некорректных последовательностей на границе prev и input, – и можно переходить к следующему блоку. Эта проверка осуществляется аналогично проверке в конце входной строки; беззнаковое векторное сравнение с [..., 0xС0, 0xE0, 0xC0], которого нет на Intel, заменяется на вычисление векторного максимума (pmaxub) и его сравнение с тем же вектором.Проверка на ASCII оказывается единственным ветвлением внутри итерации валидатора, и для успешного предсказания этого ветвления достаточно, чтобы во входной строке не чередовались блоки целиком из ASCII со блоками, содержащими не-ASCII-символы. Исследователи обнаружили, что ещё лучших результатов на реальных текстах удаётся добиться, проверяя на ASCII объединение по OR четырёх соседних блоков, и пропуская все четыре блока в случае ASCII. И действительно: можно ожидать, что если автор текста в принципе пользуется не-ASCII-символами, то они будут встречаться как минимум раз на 64 символа, чего достаточно для предсказания перехода.



AlexanderYurev
Ничего не понял, но звучит очень круто!